概率与统计常考小题归类(15大核心考点) -2024年高考数学二轮复习 课件(共47张PPT)
文档属性
| 名称 | 概率与统计常考小题归类(15大核心考点) -2024年高考数学二轮复习 课件(共47张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-25 00:00:00 | ||
图片预览











文档简介
(共47张PPT)
概率与统计常考小题归类
2024
高考二轮复习讲练测
01
02
03
04
目录
CONTENTS
考情分析
知识建构
核心考点
方法技巧
真题研析
01
PART ONE
考情分析
稿定PPT
稿定PPT,海量素材持续更新,上千款模板选择总有一款适合你
02
概率与统计小题是每年高考必考的内容.一是求统计图表、方差、平均数;二是求古典概型;三是相互独立事件和相互独立事件的概率乘法公式.多以选择、填空题的形式考查,难度容易或中等.
稿定PPT
稿定PPT,海量素材持续更新,上千款模板选择总有一款适合你
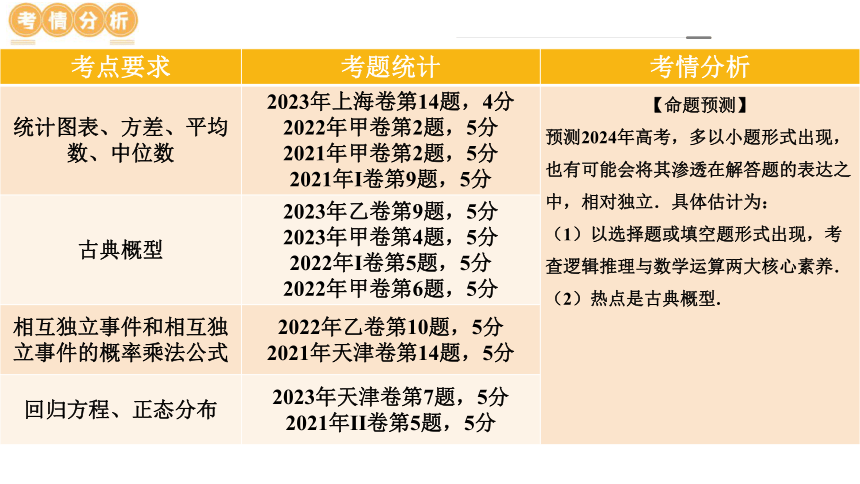
考点要求 考题统计 考情分析
统计图表、方差、平均数、中位数 2023年上海卷第14题,4分 2022年甲卷第2题,5分 2021年甲卷第2题,5分 2021年I卷第9题,5分 【命题预测】
预测2024年高考,多以小题形式出现,也有可能会将其渗透在解答题的表达之中,相对独立.具体估计为:
(1)以选择题或填空题形式出现,考查逻辑推理与数学运算两大核心素养.
(2)热点是古典概型.
古典概型 2023年乙卷第9题,5分 2023年甲卷第4题,5分 2022年I卷第5题,5分 2022年甲卷第6题,5分 相互独立事件和相互独立事件的概率乘法公式 2022年乙卷第10题,5分 2021年天津卷第14题,5分 回归方程、正态分布 2023年天津卷第7题,5分 2021年II卷第5题,5分
02
PART TWO
知识建构
03
PART THREE
方法技巧
真题研析
1、加强识图能力,理解并记准频率分布直方图与众数、中位数及平均数的关系;折线图注意上升趋势以及波动性;扇形图数据可先用表格列出,再计算、判断.
2、在频率分布直方图中,注意小矩形的,小矩形的面积,所有小矩形的面积之和为1.
3、求回归方程
(1)根据散点图判断两变量是否线性相关,如不是,应通过换元构造线性相关.
(2)利用公式,求出回归系数.
(3)待定系数法:利用回归直线过样本点的中心求系数.
4、回归方程的拟合效果,可以利用相关系数判断,当越趋近于1时,两变量的线性相关性越强.
5、比较几个分类变量有关联的可能性大小的方法
(1)通过计算的大小判断:越大,两变量有关联的可能性越大.
(2)通过计算的大小判断:越大,两变量有关联的可能性越大.
6、独立性检验的一般步骤
(1)根据样本数据制成列联表.
(2)根据公式,计算的观测值.
(3)比较与临界值的大小关系,进行统计推断.
7、概率分布与不同知识背景结合考查对实际问题的解决能力
(1)与数列结合的实际问题
(2)与函数导数结合的实际问题
(3)与分段函数求最值、解不等式结合的实际问题
(4)与统计结合的实际问题
(5)与其他背景结合的实际问题
1.(2023 乙卷)某学校举办作文比赛,共6个主题,每位参赛同学从中随机抽取一个主题准备作文,则甲、乙两位参赛同学抽到不同主题概率为
A. B. C. D.
2.(2023 甲卷)某校文艺部有4名学生,其中高一、高二年级各2名.从这4名学生中随机选2名组织校文艺汇演,则这2名学生来自不同年级的概率为
A. B. C. D.
3.(2022 新高考Ⅰ)从2至8的7个整数中随机取2个不同的数,则这2个数互质的概率为
A. B. C. D.
4.(2022 乙卷)某棋手与甲、乙、丙三位棋手各比赛一盘,各盘比赛结果相互独立.已知该棋手与甲、乙、丙比赛获胜的概率分别为,,,且.记该棋手连胜两盘的概率为,则
A.与该棋手和甲、乙、丙的比赛次序无关 B.该棋手在第二盘与甲比赛,最大
C.该棋手在第二盘与乙比赛,最大 D.该棋手在第二盘与丙比赛,最大
A
D
D
D
04
PART FOUR
核心考点
【例1】(2024·青海西宁·高三统考期末)用分层抽样的方法从某社区的500名男居民和700名女居民中选
取12人参与社区服务满意度调研,则女居民比男居民多选取( )
A.8人 B.6人 C.4人 D.2人
【答案】D
【解析】由题可知,男居民选取人,女居民选取人,
则女居民比男居民多选取2人.
故选:D.
考点题型一:抽样方法与随机数表
【变式1-1】(2024·全国·高三专题练习)总体由编号为01,02,…,19,20的20个个体组成,利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )
A.08 B.02 C.63 D.01
【答案】D
【解析】根据题意,依次读出的数据为65(舍去),72(舍去),08,02,63(舍去),14,07,02(舍去,重复),43(舍去),69(舍去),97(舍去),28(舍去),01.即第5个数字为01.
故选:D.
考点题型一:抽样方法与随机数表
【例2】(多选题)江西省2017年到2022年常住人口变化图如图所示,则( )
A.江西省2017年到2022年这6年的常住人口在2019年取得最大值
B.江西省2017年到2022年这6年的常住人口的极差为148.70万
C.江西省2017年到2022年这6年的常住人口的中位数为4527.98万
D.江西省2017年到2022年这6年的常住人口的第80百分位数为4647.60万
【答案】ABD
【解析】由图可知,将江西省2017年到2022年这6年的常住人口(单位:万)按照从小到大的顺序排列为4517.40,4518.86,4527.98,4622.10,4647.60,4666.10,
对于A项,这6年的常住人口在2019年取得最大值,故A项正确;
对于B项,极差为万,故B项正确;
对于C项,中位数为万,故C项错误;
对于D项,因为,所以第80百分位数为4647.60万,故D项正确.
故选:ABD.
考点题型二:统计图表及其数字特征
【变式2-1】(多选题)(2024·广东惠州·高三惠州一中校考阶段练习)某地环境部门对辖区内甲、乙、丙、丁四个地区的环境治理情况进行检查督导,若一地区连续10天每天的空气质量指数均不大于100,则认为该地区的环境治理达标,否则认为该地区的环境治理不达标.根据连续10天检测所得数据的数字特征推断,环境治理一定达标的地区是( )
A.甲地区:平均数为90,方差为10 B.乙地区:平均数为60,众数为50
C.丙地区:中位数为50,极差为70 D.丁地区:极差为20,80%分位数为80
【答案】AD
【解析】设每天的空气质量指数为(,2,…,10),则方差.
对于A,由,得,若这10天中有1天的空气质量指数大于100,则必有,矛盾,所以这10天每天的空气质量指数都不大于100,故A正确;
对于B,假设有8天为50,有1天为140,有1天为60,此时平均数为60,众数为50,但该地区的环境治理不达标,故B错误;
对于C,假设第1天为120,后面9天为50,此时中位数为50,极差为70,但该地区的环境治理不达标,故错误;
对于D,如果最大值大于100,根据极差为20,则最小值大于80,这与分位数为80矛盾,故最大值不大于100,故D正确.
故选:AD
考点题型二:统计图表及其数字特征
【变式2-2】(多选题)(2024·广东珠海·高三珠海市第一中学校考期末)某单位为了解职工健康情况,采用分层随机抽样的方法从5000名职工中抽取了一个容量为100的样本.其中,男性平均体重为64千克,方差为151;女性平均体重为56千克,方差为159,男女人数之比为,下列说法正确的是( )
A.样本为该单位的职工 B.每一位职工被抽中的可能性为
C.该单位职工平均体重 D.单位职工的方差
【答案】BCD
【解析】A项,样本为该单位的职工的健康情况,所以A项错误;
B项,由题可知,每一位职工被抽中的可能性为,所以B项正确;
C项,D项,设设男性人数为,女性人数为,
该单位全体人员体重的平均数为:,
,
所以C、D项正确;
故选:BCD.
考点题型二:统计图表及其数字特征
【例3】某科学兴趣小组的同学认为生物都是由蛋白质构成的,高温可以使蛋白质变性失活,于是想初步探究某微生物的成活率与温度的关系,微生物数量(个)与温度的部分数据如下表:
由表中数据算得回归方程为,预测当温度为时,微生物数量为 个.
【答案】9
【解析】由表格数据可知,
,
,
因为点在直线上,
所以,
即,故当时,,
即预测当温度为时,微生物数量为9个.
故答案为:9
考点题型三:传统线性拟合
【变式3-1】(2024·广东深圳·高三统考期末)某同学收集了变量,的相关数据如下:
为了研究,的相关关系,他由最小二乘法求得关于的线性回归方程为,经验证回归直线正好经过样本点,则 .
【答案】69
【解析】因为线性回归方程经过样本点,所以.
因为:,
所以.
所以:.
故答案为:69
考点题型三:传统线性拟合
【例4】(2024·内蒙古呼和浩特·高三统考期末)用模型拟合一组数据组,
其中,设,得变换后的线性回归方程为,则( )
A. B. C.35 D.21
【答案】B
【解析】由题意得,
故,
即,
故,解得.
故选:B
考点题型四:非线性拟合处理
【变式4-1】(2024·四川宜宾·四川省宜宾市南溪第一中学校校考模拟预测)下表为某外来生物物种入侵某河流生态后的前3个月繁殖数量(单位:百只)的数据,通过相关理论进行分析,知可用回归模型对与的关系进行拟合,则根据该回归模型,预测第7个月该物种的繁殖数量为( )
A.百只 B.百只 C.百只 D.百只
【答案】D
【解析】由题意,两边取自然对数得,
令,则,,
,
∵回归直线必过样本点的中心,∴,
得,∴,则,
当时,.故选:D.
考点题型四:非线性拟合处理
【例5】(2024·全国·高三专题练习)为了解喜爱足球是否与性别有关,随机抽取了若干人进行调查,抽取女性人数是男性的2倍,男性喜爱足球的人数占男性人数的,女性喜爱足球的人数占女性人数的,若本次调查得出“在犯错误的概率不超过0.005的前提下认为喜爱足球与性别有关”的结论,则被调查的男性至少有( )人
A.11 B.12 C.13 D.14
【答案】B
【解析】设男性人数为,依题意,得列联表如表:
则的观测值为,
因为本次调查得出“在犯错误的概率不超过0.005的前提下认为喜爱足球与性别有关”的结论,
于是,即,解得,而,因此
故选:B
考点题型五:传统独立性检验
【变式5-1】(2024·四川达州·统考一模)四川省将从2022年秋季入学的高一年级学生开始实行高考综合改革,高考采用“3+1+2”模式,其中“1”为首选科目,即物理与历史二选一.某校为了解学生的首选意愿,对部分高一学生进行了抽样调查,制作出如下两个等高条形图,根据条形图信息,下列结论正确的是( )
A.样本中选择物理意愿的男生人数少于选择历史意愿的女生人数
B.样本中女生选择历史意愿的人数多于男生选择历史意愿的人数
C.样本中选择物理学科的人数较多
D.样本中男生人数少于女生人数
【答案】C
【解析】根据等高条形图图1可知样本中选择物理学科的人数较多,故C正确;
根据等高条形图图2可知样本中男生人数多于女生人数,故D错误;
样本中选择物理学科的人数多于选择历史意愿的人数,而选择物理意愿的男生比例高,选择历史意愿的女生比例低,
所以样本中选择物理意愿的男生人数多于选择历史意愿的女生人数,故A错误;
样本中女生选择历史意愿的人数不一定多于男生选择历史意愿的人数,故B错误.
故选:C.
考点题型五:传统独立性检验
【例6】(多选题)(2024·全国·模拟预测)教育统计学中,为了解某考生的成绩在全体考生成绩中的位置,通常将考生的原始分数转化为标准分数.定义标准分数,其中为原始分数,为原始分数的平均数,为原始分数的标准差.已知某校的一次数学考试,全体考生的平均成绩,标准差,转化为标准分数后,记平均成绩为,标准差为,则( )
A. B. C. D.
【答案】BD
【解析】根据平均数与方差公式,
得,
,
即,.
故选:BD.
考点题型六:创新类定义统计
【变式6-1】(2024·湖北·高三校联考开学考试)定义空间直角坐标系中的任意点的“数”为:在点的坐标中不同数字的个数,如:,若点的坐标,则所有这些点的“数”的平均值为( )
A. B. C. D.
【答案】A
【解析】由题意,点的坐标中不同数字的个数,可分为三类:
(1)恰有3个相同数字的排列为种,则共有个;
(2)恰有2个相同数字的排列为种,则共有个;
(3)恰有0个相同数字的排列为种,则共有个;
所以平均值为
故选:A.
考点题型六:创新类定义统计
【例7】已知某社区居民每周运动总时间为随机变量(单位:小时),且,.现从该社区中随机抽取3名居民,则至少有两名居民每周运动总时间为5至6小时的概率为( )
A.0.642 B.0.648 C.0.722 D.0.748
【答案】B
【解析】由题意得,
则,
则,
则至少有两名居民每周运动总时间为5至6小时的概率为,
故选:B.
考点题型七:正态分布
【变式7-1】(2024·重庆·高三重庆八中校考阶段练习)阿鑫上学有时坐公交车,有时骑自行车.若阿鑫坐公交车用时X和骑自行车用时Y都服从正态分布,其密度曲线如图所示,则以下结论错误的是( )
A.Y的数据较X更集中 B.若有34min可用,那么坐公交车不迟到的概率大
C.若有38min可用,那么骑自行车不迟到的概率大 D.
【答案】D
【解析】观察图象知,,
对于A,的密度曲线瘦高、的密度曲线矮胖,即随机变量的标准差小于的标准差,即,
因此Y的数据较X更集中,A正确;
对于B,显然,则当有34min可用时,坐公交车不迟到的概率大,B正确;
对于C,显然,则当有38min可用时,骑自行车不迟到的概率大,C正确;
对于D,显然,因此,D错误.
故选:D
考点题型七:正态分布
【变式7-2】(2024·全国·模拟预测)某早餐店发现加入网络平台后,每天小笼包的销售量(单位:个),估计300天内小笼包的销售量约在950到1100个的天数大约是( )
(若随机变量,则,,)
A.236 B.246 C.270 D.275
【答案】B
【解析】由题可知,,,
.
所以300天内小笼包的销售量约在950到1100个的天数大约是天.
故选:B.
考点题型七:正态分布
【例8】(2023上·上海浦东新·高三统考期末)在100件产品中有90件一等品、10件二等品,从中随机抽取3件产品,则恰好含1件二等品的概率为 (结果精确到0.01).
【答案】0.25
【解析】从这批产品中抽取3件,则事件总数为,
其中恰好有一件二等品的事件有,
所以恰好有一件二等品的概率为.
故答案为:0.25
考点题型八:超几何分布与二项分布
【变式8-1】(2023·浙江金华·校联考模拟预测)一次掷两枚骰子,若两枚骰子点数之和为4或5或6,则称这是一次成功试验.现进行四次试验,则恰出现一次成功试验的概率为 .
【答案】
【解析】一次掷两枚骰子,两枚骰子点数之和为4的情况有3种,
两枚骰子点数之和为5的情况有4种,
两枚骰子点数之和为6的情况有5种,
在一次试验中,出现成功试验的概率,
设出现成功试验的次数为,则,
所以重复做这样的试验4次,则恰出现一次成功试验的概率为,
故答案为:.
考点题型八:超几何分布与二项分布
【变式8-2】(2023上·江苏常州·高三常州高级中学校考开学考试)设随机变量,记,.在研究的最大值时,某学习小组发现并证明了如下正确结论:若为正整数,当时,,此时这两项概率均为最大值;若不为正整数,则当且仅当取的整数部分时,取最大值.某同学重复投掷一枚质地均匀的骰子并实时记录点数1出现的次数.当投掷到第20次时,记录到此时点数1出现4次,若继续再进行80次投掷试验,则在这100次投掷试验中,点数1总共出现的次数为 的概率最大.
【答案】17
【解析】继续再进行80次投掷试验,出现点数为1次数服从二项分布,
由,结合题中结论可知,时概率最大,即后面80次中出现13次点数1的概率最大,
加上前面20次中的4次,所以出现17次的概率最大.
故答案为:17.
考点题型八:超几何分布与二项分布
【例9】(2024·全国·高三专题练习)某同学参加学校数学知识竞赛,规定每个同学答20道题,已知该同学每道题答对的概率为0.6,每道题答对与否相互独立.若答对一题得3分,答错一题扣1分,则该同学总得分的数学期望为 ,方差为 .
【答案】 28 76.8
【解析】设该同学答对题目的数量为,因为该同学每道题答对的概率为,共答道题,
所以,所以,
.
设该同学总得分为,则,,
.
故答案为:;.
考点题型九:随机变量的分布列、期望、方差
【变式9-1】(2024·全国·高三专题练习)有一批产品,其中有12件正品和4件次品,从中有放回地任取3件,若X表示取到次品的次数,则 , .
【答案】
【解析】由题意得服从二项分布,且每次取到次品的概率为,所以,
所以,
.
故答案为:;.
考点题型九:随机变量的分布列、期望、方差
【例10】(2024·全国·模拟预测)某艺术展览会的工作人员要将A,B,C三幅作品排成一排,则A,B这两幅作品排在一起的概率为 .
【答案】
【解析】根据题意A,B,C三幅作品排成一行,有ABC,ACB,BAC,BCA,CBA,CAB共6种情况,
A,B这两幅作品排在一起的情况有ABC,BAC,CBA,CAB,共4种,
则A,B这两幅作品排在一起的概率.
故答案为:
考点题型十:古典概型
【变式10-1】(2024·全国·模拟预测)2023年10月18日,第三届“一带一路”国际合作高峰论坛在北京举行.在“一带一路”欢迎晚宴上,我国拿出特有的美食、美酒款待大家,让国际贵宾们感受中国饮食文化、茶文化、酒文化.这次晚宴菜单中有“全家福”“沙葱牛肉”“北京烤鸭”“什锦鲜蔬”“冰花锅贴”“蟹黄烧麦”“天鹅酥”“象形枇杷”.假设在上菜的过程中服务员随机上这八道菜(每次只上一道菜),则“沙葱牛肉”“北京烤鸭”相邻的概率为 .
【答案】
【解析】服务员随机上这八道菜有种排法,
“沙葱牛肉”,“北京烤鸭”相邻有种排法,
所以所求概率.
故答案为:.
考点题型十:古典概型
【例11】(2024·山东滨州·高三统考期末)甲和乙两个箱子中各装有10个除颜色外完全相同的球,其中甲箱中有4个红球、3个白球和3个黑球,乙箱中有5个红球、2个白球和3个黑球.先从甲箱中随机取出一球放入乙箱,分别用、和表示由甲箱取出的球是红球、白球和黑球的事件;再从乙箱中随机取出一球,用B表示由乙箱取出的球是红球的事件,则
【答案】
【解析】由题意得,,,
若发生,此时乙箱中有6个红球,2个白球和3个黑球,则,
先发生,此时乙箱中有5个红球,3个白球和3个黑球,则,
先发生,此时乙箱中有5个红球,2个白球和4个黑球,则.
, ;
.故答案为:
考点题型十一:条件概率与全概率
【变式11-1】(2024·河南·模拟预测)设同一随机试验中的两个事件A,B满足,,,则 .
【答案】
【解析】由,得;
由全概率公式:,
则.
故答案是:.
考点题型十一:条件概率与全概率
【例12】(2024·黑龙江大庆·铁人中学校考模拟预测)如图是一块高尔顿板示意图:在一块木板.上钉着若干排互相平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,小球从上方的通道口落下后,将与层层小木块碰撞,最后掉入下方的某一个球槽内.若小球下落过程中向左、向右落下的机会均等,则小球最终落入④号球槽的的概率为( )
A. B. C. D.
【答案】D
【解析】设这个球落入④号球槽为时间,落入④号球槽要经过两次向左,三次向右,
所以.
故选:D.
考点题型十二:概统结合问题
【变式12-1】(2024·海南·统考模拟预测)我国实行个人所得税专项附加扣除制度,涉及子女教育、继续教育、大病医疗、住房贷款利息、住房租金、赡养老人等多项专项附加扣除.某单位老年、中年、青年员工分别有90人、270人、180人,现采用分层抽样的方法,从该单位上述员工中抽取6人调查专项附加扣除的情况,再从这6人中任选2人,则选取的2人中恰有一名是中年员工的概率为( )
A. B. C. D.
【答案】B
【解析】由分层抽样等比例性质知:老年、中年、青年员工分别抽取了1人、3人、2人,
所以6人中任选2人中恰有一名是中年员工的概率为
.
故选:B
考点题型十二:概统结合问题
【例13】(2024·浙江宁波·效实中学校考模拟预测)盒中有5个小球,其中3个白球,2个黑球,从中任取个球,在取出的球中,黑球放回,白球涂黑后放回,此时盒中黑球的个数记为,则( )
A., B.,
C., D.,
【答案】C
【解析】,,
∵,∴ .
∵,,,
∴,故选:C.
考点题型十三:传统规则的概率问题
【变式13-1】(2024·广东清远·高二统考期末)盒中有a个红球,b个黑球,c个白球,今随机地从中取出一个,观察其颜色后放回,并加上同色球d个,再从盒中抽取一球,则第二次抽出的是黑球的概率是( )
A. B. C. D.
【答案】A
【解析】设事件“第一次抽出的是红球”,事件“第一次抽出的是黑球”,事件“第一次抽出的是白球”,事件“第二次抽出的是黑球”.
由全概率公式知
由题意,,,,,,则,
故选:A
考点题型十三:传统规则的概率问题
【例14】(2024·河南信阳·高二统考期末)2022年卡塔尔世界杯决赛中,阿根廷队与法国队在120分钟比赛中战平,经过四轮点球大战阿根廷队以总分战胜法国队,第三次获得世界杯冠军.其中门将马丁内斯扑出法国队员的点球,表现神勇,扑点球的难度一般比较大,假设罚点球的球员会等可能地随机选择球门的左、中、右三个方向射门,门将也会等可能地随机选择球门的左、中、右三个方向来扑点球,而且门将即使方向判断正确也有的可能性扑不到球.若不考虑其他因素,在点球大战中,门将在前四次扑出点球的个数X的期望为( )
A. B. C. D.2
【答案】C
【解析】依题意可得,门将每次可以扑出点球的概率为.
门将在前四次扑出点球的个数X可能的取值为0,1,2,3,4.,
,,1,2,3,4.
期望.
故选:C.
考点题型十四:新赛制概率问题
【变式14-1】通过核酸检测可以初步判定被检测者是否感染新冠病毒,检测方式分为单检和混检.单检,是将一个人的采集拭子放入一个采样管中单独检测;混检,是将多个人的采集拭子放入一个采样管中合为一个样本进行检测,若检测结果呈阳性,再对这多个人重新采集单管拭子,逐一进行检测,以确定当中的阳性样本.混检按一个采样管中放入的采集拭子个数可具体分为“3合1”混检,“5合1”混检,“10合1”混检等.调查研究显示,在群体总阳性率较低(低于0.1%)时,混检能较大幅度地提高检测效力、降低检测成本.根据流行病学调查结果显示,某城市居民感染新冠病毒的概率为0.0005.若对该城市全体居民进行核酸检测,记采用“10合1”混检方式共需检测X次,采用“5合1”混检方式共需检测Y次,已知当时,,据此计算的近似值为( )
A. B. C. D.
【答案】B
【解析】由于一个城市的总人口数很大,而总体阳性率较低,所以我们可以认为阳性个体均匀分布,
若进行10合1混检,对任意一个10人组进行检测,总检测次数有两种结果:1次和11次,
概率分别为和,故这10人组检测次数的期望为,
相当于每个个体平均检测次,同理,采用5合1混检,每个个体平均检测次,
∴.
故选:B
考点题型十四:新赛制概率问题
【例15】(2024上·甘肃·高三统考阶段练习)某学校有、两个餐厅,已知同学甲每天中午都会在这两个餐厅中选择一个就餐,如果甲当天选择了某个餐厅,他第二天会有的可能性换另一个餐厅就餐,假如第天甲选择了餐厅,则第天选择餐厅的概率为 .
【答案】
【解析】当且时,若甲在第天选择了餐厅,
那么在第天有的可能性选择餐厅,
若甲在第天选择了餐厅,那么在第天有的可能性选择餐厅,
所以第天选择餐厅的概率,
即,所以.
又由题意得,,
所以是以为首项,为公比的等比数列,
所以,
所以.
故答案为:.
考点题型十五:递推型概率命题
【变式15-1】(2022下·湖北·高三宜城市第一中学校联考阶段练习)五名运动员、、、、相互传球.每个人在接到球后随机传给其他四人中的一人.设首先由开始进行第次传球,那么恰好在第次传球把球传回到手中的概率是 (用最简分数表示).
【答案】
【解析】设第次传球把球传回到的手中的概率为,第次传球将球传给其他运动员,故;
表示第次传球把球传回到的手中,故传球前球不在手中,
而每名运动员传给其他一名指定运动员的概率为,由乘法原理,故.
于是,且,故数列为首项为,公比为的等比数列,
于是,即,,
故.故答案为:.
考点题型十五:递推型概率命题
感谢观看
THANK YOU
概率与统计常考小题归类
2024
高考二轮复习讲练测
01
02
03
04
目录
CONTENTS
考情分析
知识建构
核心考点
方法技巧
真题研析
01
PART ONE
考情分析
稿定PPT
稿定PPT,海量素材持续更新,上千款模板选择总有一款适合你
02
概率与统计小题是每年高考必考的内容.一是求统计图表、方差、平均数;二是求古典概型;三是相互独立事件和相互独立事件的概率乘法公式.多以选择、填空题的形式考查,难度容易或中等.
稿定PPT
稿定PPT,海量素材持续更新,上千款模板选择总有一款适合你
考点要求 考题统计 考情分析
统计图表、方差、平均数、中位数 2023年上海卷第14题,4分 2022年甲卷第2题,5分 2021年甲卷第2题,5分 2021年I卷第9题,5分 【命题预测】
预测2024年高考,多以小题形式出现,也有可能会将其渗透在解答题的表达之中,相对独立.具体估计为:
(1)以选择题或填空题形式出现,考查逻辑推理与数学运算两大核心素养.
(2)热点是古典概型.
古典概型 2023年乙卷第9题,5分 2023年甲卷第4题,5分 2022年I卷第5题,5分 2022年甲卷第6题,5分 相互独立事件和相互独立事件的概率乘法公式 2022年乙卷第10题,5分 2021年天津卷第14题,5分 回归方程、正态分布 2023年天津卷第7题,5分 2021年II卷第5题,5分
02
PART TWO
知识建构
03
PART THREE
方法技巧
真题研析
1、加强识图能力,理解并记准频率分布直方图与众数、中位数及平均数的关系;折线图注意上升趋势以及波动性;扇形图数据可先用表格列出,再计算、判断.
2、在频率分布直方图中,注意小矩形的,小矩形的面积,所有小矩形的面积之和为1.
3、求回归方程
(1)根据散点图判断两变量是否线性相关,如不是,应通过换元构造线性相关.
(2)利用公式,求出回归系数.
(3)待定系数法:利用回归直线过样本点的中心求系数.
4、回归方程的拟合效果,可以利用相关系数判断,当越趋近于1时,两变量的线性相关性越强.
5、比较几个分类变量有关联的可能性大小的方法
(1)通过计算的大小判断:越大,两变量有关联的可能性越大.
(2)通过计算的大小判断:越大,两变量有关联的可能性越大.
6、独立性检验的一般步骤
(1)根据样本数据制成列联表.
(2)根据公式,计算的观测值.
(3)比较与临界值的大小关系,进行统计推断.
7、概率分布与不同知识背景结合考查对实际问题的解决能力
(1)与数列结合的实际问题
(2)与函数导数结合的实际问题
(3)与分段函数求最值、解不等式结合的实际问题
(4)与统计结合的实际问题
(5)与其他背景结合的实际问题
1.(2023 乙卷)某学校举办作文比赛,共6个主题,每位参赛同学从中随机抽取一个主题准备作文,则甲、乙两位参赛同学抽到不同主题概率为
A. B. C. D.
2.(2023 甲卷)某校文艺部有4名学生,其中高一、高二年级各2名.从这4名学生中随机选2名组织校文艺汇演,则这2名学生来自不同年级的概率为
A. B. C. D.
3.(2022 新高考Ⅰ)从2至8的7个整数中随机取2个不同的数,则这2个数互质的概率为
A. B. C. D.
4.(2022 乙卷)某棋手与甲、乙、丙三位棋手各比赛一盘,各盘比赛结果相互独立.已知该棋手与甲、乙、丙比赛获胜的概率分别为,,,且.记该棋手连胜两盘的概率为,则
A.与该棋手和甲、乙、丙的比赛次序无关 B.该棋手在第二盘与甲比赛,最大
C.该棋手在第二盘与乙比赛,最大 D.该棋手在第二盘与丙比赛,最大
A
D
D
D
04
PART FOUR
核心考点
【例1】(2024·青海西宁·高三统考期末)用分层抽样的方法从某社区的500名男居民和700名女居民中选
取12人参与社区服务满意度调研,则女居民比男居民多选取( )
A.8人 B.6人 C.4人 D.2人
【答案】D
【解析】由题可知,男居民选取人,女居民选取人,
则女居民比男居民多选取2人.
故选:D.
考点题型一:抽样方法与随机数表
【变式1-1】(2024·全国·高三专题练习)总体由编号为01,02,…,19,20的20个个体组成,利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )
A.08 B.02 C.63 D.01
【答案】D
【解析】根据题意,依次读出的数据为65(舍去),72(舍去),08,02,63(舍去),14,07,02(舍去,重复),43(舍去),69(舍去),97(舍去),28(舍去),01.即第5个数字为01.
故选:D.
考点题型一:抽样方法与随机数表
【例2】(多选题)江西省2017年到2022年常住人口变化图如图所示,则( )
A.江西省2017年到2022年这6年的常住人口在2019年取得最大值
B.江西省2017年到2022年这6年的常住人口的极差为148.70万
C.江西省2017年到2022年这6年的常住人口的中位数为4527.98万
D.江西省2017年到2022年这6年的常住人口的第80百分位数为4647.60万
【答案】ABD
【解析】由图可知,将江西省2017年到2022年这6年的常住人口(单位:万)按照从小到大的顺序排列为4517.40,4518.86,4527.98,4622.10,4647.60,4666.10,
对于A项,这6年的常住人口在2019年取得最大值,故A项正确;
对于B项,极差为万,故B项正确;
对于C项,中位数为万,故C项错误;
对于D项,因为,所以第80百分位数为4647.60万,故D项正确.
故选:ABD.
考点题型二:统计图表及其数字特征
【变式2-1】(多选题)(2024·广东惠州·高三惠州一中校考阶段练习)某地环境部门对辖区内甲、乙、丙、丁四个地区的环境治理情况进行检查督导,若一地区连续10天每天的空气质量指数均不大于100,则认为该地区的环境治理达标,否则认为该地区的环境治理不达标.根据连续10天检测所得数据的数字特征推断,环境治理一定达标的地区是( )
A.甲地区:平均数为90,方差为10 B.乙地区:平均数为60,众数为50
C.丙地区:中位数为50,极差为70 D.丁地区:极差为20,80%分位数为80
【答案】AD
【解析】设每天的空气质量指数为(,2,…,10),则方差.
对于A,由,得,若这10天中有1天的空气质量指数大于100,则必有,矛盾,所以这10天每天的空气质量指数都不大于100,故A正确;
对于B,假设有8天为50,有1天为140,有1天为60,此时平均数为60,众数为50,但该地区的环境治理不达标,故B错误;
对于C,假设第1天为120,后面9天为50,此时中位数为50,极差为70,但该地区的环境治理不达标,故错误;
对于D,如果最大值大于100,根据极差为20,则最小值大于80,这与分位数为80矛盾,故最大值不大于100,故D正确.
故选:AD
考点题型二:统计图表及其数字特征
【变式2-2】(多选题)(2024·广东珠海·高三珠海市第一中学校考期末)某单位为了解职工健康情况,采用分层随机抽样的方法从5000名职工中抽取了一个容量为100的样本.其中,男性平均体重为64千克,方差为151;女性平均体重为56千克,方差为159,男女人数之比为,下列说法正确的是( )
A.样本为该单位的职工 B.每一位职工被抽中的可能性为
C.该单位职工平均体重 D.单位职工的方差
【答案】BCD
【解析】A项,样本为该单位的职工的健康情况,所以A项错误;
B项,由题可知,每一位职工被抽中的可能性为,所以B项正确;
C项,D项,设设男性人数为,女性人数为,
该单位全体人员体重的平均数为:,
,
所以C、D项正确;
故选:BCD.
考点题型二:统计图表及其数字特征
【例3】某科学兴趣小组的同学认为生物都是由蛋白质构成的,高温可以使蛋白质变性失活,于是想初步探究某微生物的成活率与温度的关系,微生物数量(个)与温度的部分数据如下表:
由表中数据算得回归方程为,预测当温度为时,微生物数量为 个.
【答案】9
【解析】由表格数据可知,
,
,
因为点在直线上,
所以,
即,故当时,,
即预测当温度为时,微生物数量为9个.
故答案为:9
考点题型三:传统线性拟合
【变式3-1】(2024·广东深圳·高三统考期末)某同学收集了变量,的相关数据如下:
为了研究,的相关关系,他由最小二乘法求得关于的线性回归方程为,经验证回归直线正好经过样本点,则 .
【答案】69
【解析】因为线性回归方程经过样本点,所以.
因为:,
所以.
所以:.
故答案为:69
考点题型三:传统线性拟合
【例4】(2024·内蒙古呼和浩特·高三统考期末)用模型拟合一组数据组,
其中,设,得变换后的线性回归方程为,则( )
A. B. C.35 D.21
【答案】B
【解析】由题意得,
故,
即,
故,解得.
故选:B
考点题型四:非线性拟合处理
【变式4-1】(2024·四川宜宾·四川省宜宾市南溪第一中学校校考模拟预测)下表为某外来生物物种入侵某河流生态后的前3个月繁殖数量(单位:百只)的数据,通过相关理论进行分析,知可用回归模型对与的关系进行拟合,则根据该回归模型,预测第7个月该物种的繁殖数量为( )
A.百只 B.百只 C.百只 D.百只
【答案】D
【解析】由题意,两边取自然对数得,
令,则,,
,
∵回归直线必过样本点的中心,∴,
得,∴,则,
当时,.故选:D.
考点题型四:非线性拟合处理
【例5】(2024·全国·高三专题练习)为了解喜爱足球是否与性别有关,随机抽取了若干人进行调查,抽取女性人数是男性的2倍,男性喜爱足球的人数占男性人数的,女性喜爱足球的人数占女性人数的,若本次调查得出“在犯错误的概率不超过0.005的前提下认为喜爱足球与性别有关”的结论,则被调查的男性至少有( )人
A.11 B.12 C.13 D.14
【答案】B
【解析】设男性人数为,依题意,得列联表如表:
则的观测值为,
因为本次调查得出“在犯错误的概率不超过0.005的前提下认为喜爱足球与性别有关”的结论,
于是,即,解得,而,因此
故选:B
考点题型五:传统独立性检验
【变式5-1】(2024·四川达州·统考一模)四川省将从2022年秋季入学的高一年级学生开始实行高考综合改革,高考采用“3+1+2”模式,其中“1”为首选科目,即物理与历史二选一.某校为了解学生的首选意愿,对部分高一学生进行了抽样调查,制作出如下两个等高条形图,根据条形图信息,下列结论正确的是( )
A.样本中选择物理意愿的男生人数少于选择历史意愿的女生人数
B.样本中女生选择历史意愿的人数多于男生选择历史意愿的人数
C.样本中选择物理学科的人数较多
D.样本中男生人数少于女生人数
【答案】C
【解析】根据等高条形图图1可知样本中选择物理学科的人数较多,故C正确;
根据等高条形图图2可知样本中男生人数多于女生人数,故D错误;
样本中选择物理学科的人数多于选择历史意愿的人数,而选择物理意愿的男生比例高,选择历史意愿的女生比例低,
所以样本中选择物理意愿的男生人数多于选择历史意愿的女生人数,故A错误;
样本中女生选择历史意愿的人数不一定多于男生选择历史意愿的人数,故B错误.
故选:C.
考点题型五:传统独立性检验
【例6】(多选题)(2024·全国·模拟预测)教育统计学中,为了解某考生的成绩在全体考生成绩中的位置,通常将考生的原始分数转化为标准分数.定义标准分数,其中为原始分数,为原始分数的平均数,为原始分数的标准差.已知某校的一次数学考试,全体考生的平均成绩,标准差,转化为标准分数后,记平均成绩为,标准差为,则( )
A. B. C. D.
【答案】BD
【解析】根据平均数与方差公式,
得,
,
即,.
故选:BD.
考点题型六:创新类定义统计
【变式6-1】(2024·湖北·高三校联考开学考试)定义空间直角坐标系中的任意点的“数”为:在点的坐标中不同数字的个数,如:,若点的坐标,则所有这些点的“数”的平均值为( )
A. B. C. D.
【答案】A
【解析】由题意,点的坐标中不同数字的个数,可分为三类:
(1)恰有3个相同数字的排列为种,则共有个;
(2)恰有2个相同数字的排列为种,则共有个;
(3)恰有0个相同数字的排列为种,则共有个;
所以平均值为
故选:A.
考点题型六:创新类定义统计
【例7】已知某社区居民每周运动总时间为随机变量(单位:小时),且,.现从该社区中随机抽取3名居民,则至少有两名居民每周运动总时间为5至6小时的概率为( )
A.0.642 B.0.648 C.0.722 D.0.748
【答案】B
【解析】由题意得,
则,
则,
则至少有两名居民每周运动总时间为5至6小时的概率为,
故选:B.
考点题型七:正态分布
【变式7-1】(2024·重庆·高三重庆八中校考阶段练习)阿鑫上学有时坐公交车,有时骑自行车.若阿鑫坐公交车用时X和骑自行车用时Y都服从正态分布,其密度曲线如图所示,则以下结论错误的是( )
A.Y的数据较X更集中 B.若有34min可用,那么坐公交车不迟到的概率大
C.若有38min可用,那么骑自行车不迟到的概率大 D.
【答案】D
【解析】观察图象知,,
对于A,的密度曲线瘦高、的密度曲线矮胖,即随机变量的标准差小于的标准差,即,
因此Y的数据较X更集中,A正确;
对于B,显然,则当有34min可用时,坐公交车不迟到的概率大,B正确;
对于C,显然,则当有38min可用时,骑自行车不迟到的概率大,C正确;
对于D,显然,因此,D错误.
故选:D
考点题型七:正态分布
【变式7-2】(2024·全国·模拟预测)某早餐店发现加入网络平台后,每天小笼包的销售量(单位:个),估计300天内小笼包的销售量约在950到1100个的天数大约是( )
(若随机变量,则,,)
A.236 B.246 C.270 D.275
【答案】B
【解析】由题可知,,,
.
所以300天内小笼包的销售量约在950到1100个的天数大约是天.
故选:B.
考点题型七:正态分布
【例8】(2023上·上海浦东新·高三统考期末)在100件产品中有90件一等品、10件二等品,从中随机抽取3件产品,则恰好含1件二等品的概率为 (结果精确到0.01).
【答案】0.25
【解析】从这批产品中抽取3件,则事件总数为,
其中恰好有一件二等品的事件有,
所以恰好有一件二等品的概率为.
故答案为:0.25
考点题型八:超几何分布与二项分布
【变式8-1】(2023·浙江金华·校联考模拟预测)一次掷两枚骰子,若两枚骰子点数之和为4或5或6,则称这是一次成功试验.现进行四次试验,则恰出现一次成功试验的概率为 .
【答案】
【解析】一次掷两枚骰子,两枚骰子点数之和为4的情况有3种,
两枚骰子点数之和为5的情况有4种,
两枚骰子点数之和为6的情况有5种,
在一次试验中,出现成功试验的概率,
设出现成功试验的次数为,则,
所以重复做这样的试验4次,则恰出现一次成功试验的概率为,
故答案为:.
考点题型八:超几何分布与二项分布
【变式8-2】(2023上·江苏常州·高三常州高级中学校考开学考试)设随机变量,记,.在研究的最大值时,某学习小组发现并证明了如下正确结论:若为正整数,当时,,此时这两项概率均为最大值;若不为正整数,则当且仅当取的整数部分时,取最大值.某同学重复投掷一枚质地均匀的骰子并实时记录点数1出现的次数.当投掷到第20次时,记录到此时点数1出现4次,若继续再进行80次投掷试验,则在这100次投掷试验中,点数1总共出现的次数为 的概率最大.
【答案】17
【解析】继续再进行80次投掷试验,出现点数为1次数服从二项分布,
由,结合题中结论可知,时概率最大,即后面80次中出现13次点数1的概率最大,
加上前面20次中的4次,所以出现17次的概率最大.
故答案为:17.
考点题型八:超几何分布与二项分布
【例9】(2024·全国·高三专题练习)某同学参加学校数学知识竞赛,规定每个同学答20道题,已知该同学每道题答对的概率为0.6,每道题答对与否相互独立.若答对一题得3分,答错一题扣1分,则该同学总得分的数学期望为 ,方差为 .
【答案】 28 76.8
【解析】设该同学答对题目的数量为,因为该同学每道题答对的概率为,共答道题,
所以,所以,
.
设该同学总得分为,则,,
.
故答案为:;.
考点题型九:随机变量的分布列、期望、方差
【变式9-1】(2024·全国·高三专题练习)有一批产品,其中有12件正品和4件次品,从中有放回地任取3件,若X表示取到次品的次数,则 , .
【答案】
【解析】由题意得服从二项分布,且每次取到次品的概率为,所以,
所以,
.
故答案为:;.
考点题型九:随机变量的分布列、期望、方差
【例10】(2024·全国·模拟预测)某艺术展览会的工作人员要将A,B,C三幅作品排成一排,则A,B这两幅作品排在一起的概率为 .
【答案】
【解析】根据题意A,B,C三幅作品排成一行,有ABC,ACB,BAC,BCA,CBA,CAB共6种情况,
A,B这两幅作品排在一起的情况有ABC,BAC,CBA,CAB,共4种,
则A,B这两幅作品排在一起的概率.
故答案为:
考点题型十:古典概型
【变式10-1】(2024·全国·模拟预测)2023年10月18日,第三届“一带一路”国际合作高峰论坛在北京举行.在“一带一路”欢迎晚宴上,我国拿出特有的美食、美酒款待大家,让国际贵宾们感受中国饮食文化、茶文化、酒文化.这次晚宴菜单中有“全家福”“沙葱牛肉”“北京烤鸭”“什锦鲜蔬”“冰花锅贴”“蟹黄烧麦”“天鹅酥”“象形枇杷”.假设在上菜的过程中服务员随机上这八道菜(每次只上一道菜),则“沙葱牛肉”“北京烤鸭”相邻的概率为 .
【答案】
【解析】服务员随机上这八道菜有种排法,
“沙葱牛肉”,“北京烤鸭”相邻有种排法,
所以所求概率.
故答案为:.
考点题型十:古典概型
【例11】(2024·山东滨州·高三统考期末)甲和乙两个箱子中各装有10个除颜色外完全相同的球,其中甲箱中有4个红球、3个白球和3个黑球,乙箱中有5个红球、2个白球和3个黑球.先从甲箱中随机取出一球放入乙箱,分别用、和表示由甲箱取出的球是红球、白球和黑球的事件;再从乙箱中随机取出一球,用B表示由乙箱取出的球是红球的事件,则
【答案】
【解析】由题意得,,,
若发生,此时乙箱中有6个红球,2个白球和3个黑球,则,
先发生,此时乙箱中有5个红球,3个白球和3个黑球,则,
先发生,此时乙箱中有5个红球,2个白球和4个黑球,则.
, ;
.故答案为:
考点题型十一:条件概率与全概率
【变式11-1】(2024·河南·模拟预测)设同一随机试验中的两个事件A,B满足,,,则 .
【答案】
【解析】由,得;
由全概率公式:,
则.
故答案是:.
考点题型十一:条件概率与全概率
【例12】(2024·黑龙江大庆·铁人中学校考模拟预测)如图是一块高尔顿板示意图:在一块木板.上钉着若干排互相平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,小球从上方的通道口落下后,将与层层小木块碰撞,最后掉入下方的某一个球槽内.若小球下落过程中向左、向右落下的机会均等,则小球最终落入④号球槽的的概率为( )
A. B. C. D.
【答案】D
【解析】设这个球落入④号球槽为时间,落入④号球槽要经过两次向左,三次向右,
所以.
故选:D.
考点题型十二:概统结合问题
【变式12-1】(2024·海南·统考模拟预测)我国实行个人所得税专项附加扣除制度,涉及子女教育、继续教育、大病医疗、住房贷款利息、住房租金、赡养老人等多项专项附加扣除.某单位老年、中年、青年员工分别有90人、270人、180人,现采用分层抽样的方法,从该单位上述员工中抽取6人调查专项附加扣除的情况,再从这6人中任选2人,则选取的2人中恰有一名是中年员工的概率为( )
A. B. C. D.
【答案】B
【解析】由分层抽样等比例性质知:老年、中年、青年员工分别抽取了1人、3人、2人,
所以6人中任选2人中恰有一名是中年员工的概率为
.
故选:B
考点题型十二:概统结合问题
【例13】(2024·浙江宁波·效实中学校考模拟预测)盒中有5个小球,其中3个白球,2个黑球,从中任取个球,在取出的球中,黑球放回,白球涂黑后放回,此时盒中黑球的个数记为,则( )
A., B.,
C., D.,
【答案】C
【解析】,,
∵,∴ .
∵,,,
∴,故选:C.
考点题型十三:传统规则的概率问题
【变式13-1】(2024·广东清远·高二统考期末)盒中有a个红球,b个黑球,c个白球,今随机地从中取出一个,观察其颜色后放回,并加上同色球d个,再从盒中抽取一球,则第二次抽出的是黑球的概率是( )
A. B. C. D.
【答案】A
【解析】设事件“第一次抽出的是红球”,事件“第一次抽出的是黑球”,事件“第一次抽出的是白球”,事件“第二次抽出的是黑球”.
由全概率公式知
由题意,,,,,,则,
故选:A
考点题型十三:传统规则的概率问题
【例14】(2024·河南信阳·高二统考期末)2022年卡塔尔世界杯决赛中,阿根廷队与法国队在120分钟比赛中战平,经过四轮点球大战阿根廷队以总分战胜法国队,第三次获得世界杯冠军.其中门将马丁内斯扑出法国队员的点球,表现神勇,扑点球的难度一般比较大,假设罚点球的球员会等可能地随机选择球门的左、中、右三个方向射门,门将也会等可能地随机选择球门的左、中、右三个方向来扑点球,而且门将即使方向判断正确也有的可能性扑不到球.若不考虑其他因素,在点球大战中,门将在前四次扑出点球的个数X的期望为( )
A. B. C. D.2
【答案】C
【解析】依题意可得,门将每次可以扑出点球的概率为.
门将在前四次扑出点球的个数X可能的取值为0,1,2,3,4.,
,,1,2,3,4.
期望.
故选:C.
考点题型十四:新赛制概率问题
【变式14-1】通过核酸检测可以初步判定被检测者是否感染新冠病毒,检测方式分为单检和混检.单检,是将一个人的采集拭子放入一个采样管中单独检测;混检,是将多个人的采集拭子放入一个采样管中合为一个样本进行检测,若检测结果呈阳性,再对这多个人重新采集单管拭子,逐一进行检测,以确定当中的阳性样本.混检按一个采样管中放入的采集拭子个数可具体分为“3合1”混检,“5合1”混检,“10合1”混检等.调查研究显示,在群体总阳性率较低(低于0.1%)时,混检能较大幅度地提高检测效力、降低检测成本.根据流行病学调查结果显示,某城市居民感染新冠病毒的概率为0.0005.若对该城市全体居民进行核酸检测,记采用“10合1”混检方式共需检测X次,采用“5合1”混检方式共需检测Y次,已知当时,,据此计算的近似值为( )
A. B. C. D.
【答案】B
【解析】由于一个城市的总人口数很大,而总体阳性率较低,所以我们可以认为阳性个体均匀分布,
若进行10合1混检,对任意一个10人组进行检测,总检测次数有两种结果:1次和11次,
概率分别为和,故这10人组检测次数的期望为,
相当于每个个体平均检测次,同理,采用5合1混检,每个个体平均检测次,
∴.
故选:B
考点题型十四:新赛制概率问题
【例15】(2024上·甘肃·高三统考阶段练习)某学校有、两个餐厅,已知同学甲每天中午都会在这两个餐厅中选择一个就餐,如果甲当天选择了某个餐厅,他第二天会有的可能性换另一个餐厅就餐,假如第天甲选择了餐厅,则第天选择餐厅的概率为 .
【答案】
【解析】当且时,若甲在第天选择了餐厅,
那么在第天有的可能性选择餐厅,
若甲在第天选择了餐厅,那么在第天有的可能性选择餐厅,
所以第天选择餐厅的概率,
即,所以.
又由题意得,,
所以是以为首项,为公比的等比数列,
所以,
所以.
故答案为:.
考点题型十五:递推型概率命题
【变式15-1】(2022下·湖北·高三宜城市第一中学校联考阶段练习)五名运动员、、、、相互传球.每个人在接到球后随机传给其他四人中的一人.设首先由开始进行第次传球,那么恰好在第次传球把球传回到手中的概率是 (用最简分数表示).
【答案】
【解析】设第次传球把球传回到的手中的概率为,第次传球将球传给其他运动员,故;
表示第次传球把球传回到的手中,故传球前球不在手中,
而每名运动员传给其他一名指定运动员的概率为,由乘法原理,故.
于是,且,故数列为首项为,公比为的等比数列,
于是,即,,
故.故答案为:.
考点题型十五:递推型概率命题
感谢观看
THANK YOU
同课章节目录
