第28章《锐角三角函数》复习
文档属性
| 名称 | 第28章《锐角三角函数》复习 |

|
|
| 格式 | rar | ||
| 文件大小 | 273.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-02-19 00:00:00 | ||
图片预览


文档简介
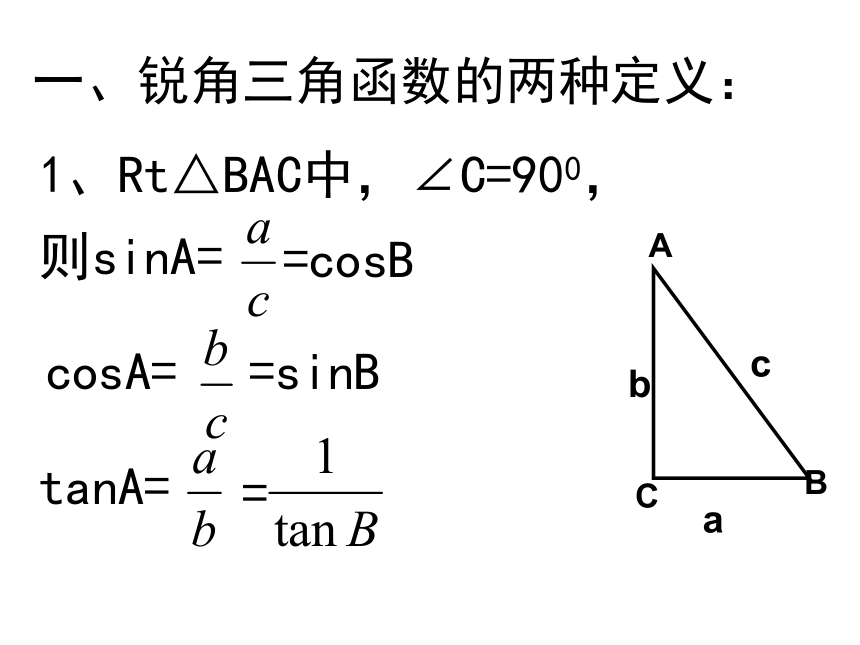
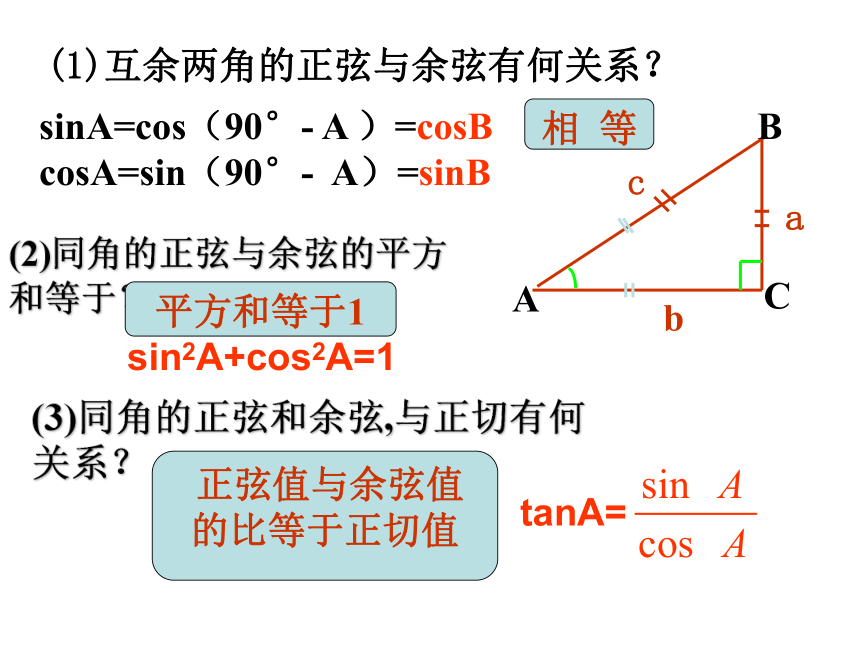
课件15张PPT。《锐角三角函数》复习一、锐角三角函数的两种定义:1、Rt△BAC中,∠C=900,abc则sinA=cosA==cosB=sinBtanA==(3)同角的正弦和余弦,与正切有何关系? 正弦值与余弦值的比等于正切值(1)互余两角的正弦与余弦有何关系?(2)同角的正弦与余弦的平方和等于? 平方和等于1相 等sin2A+cos2A=1sinA=cos(90°- A )=cosB
cosA=sin(90°- A)=sinB1. 与cos70°值相等的是( )
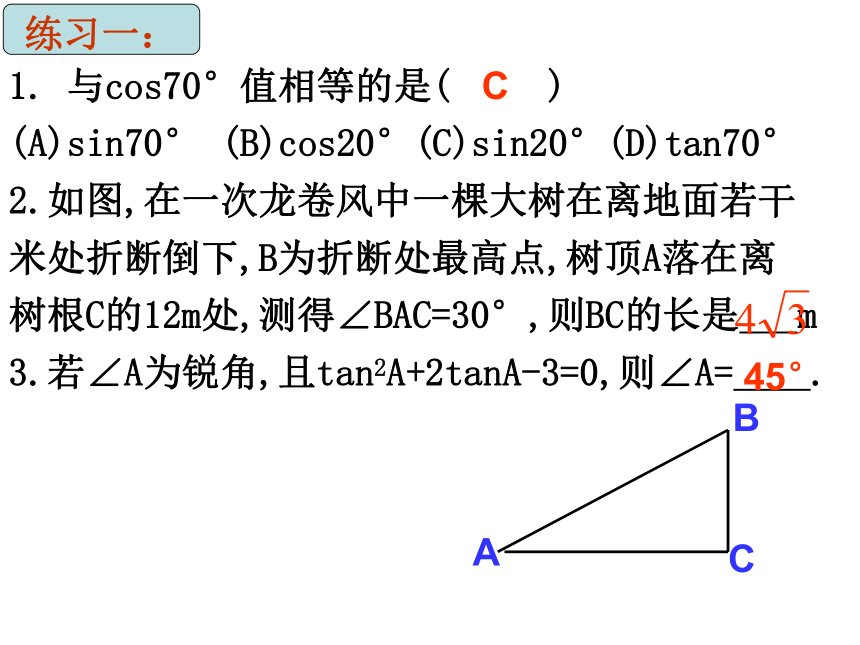
(A)sin70° (B)cos20°(C)sin20°(D)tan70°
2.如图,在一次龙卷风中一棵大树在离地面若干
米处折断倒下,B为折断处最高点,树顶A落在离
树根C的12m处,测得∠BAC=30°,则BC的长是 m
3.若∠A为锐角,且tan2A+2tanA-3=0,则∠A= .
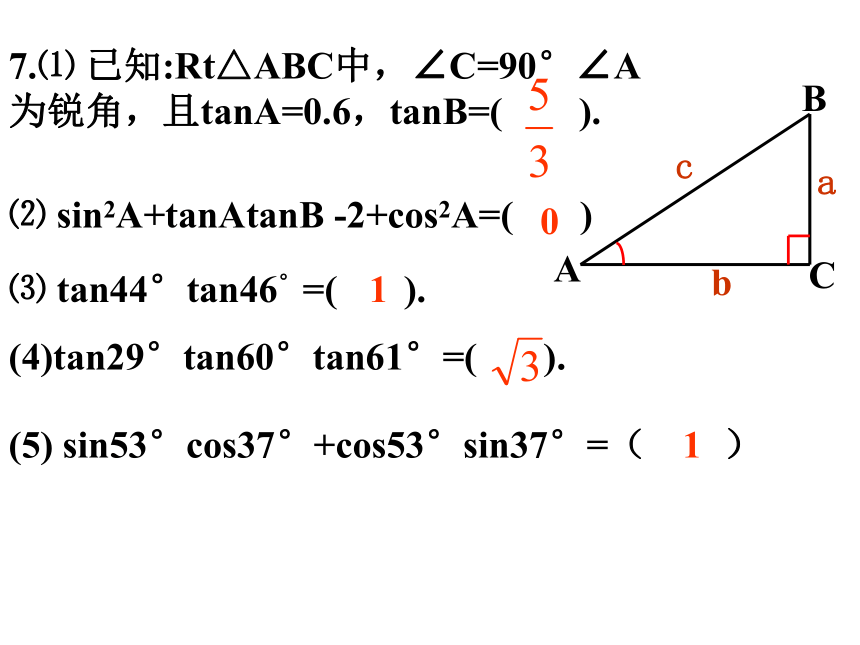
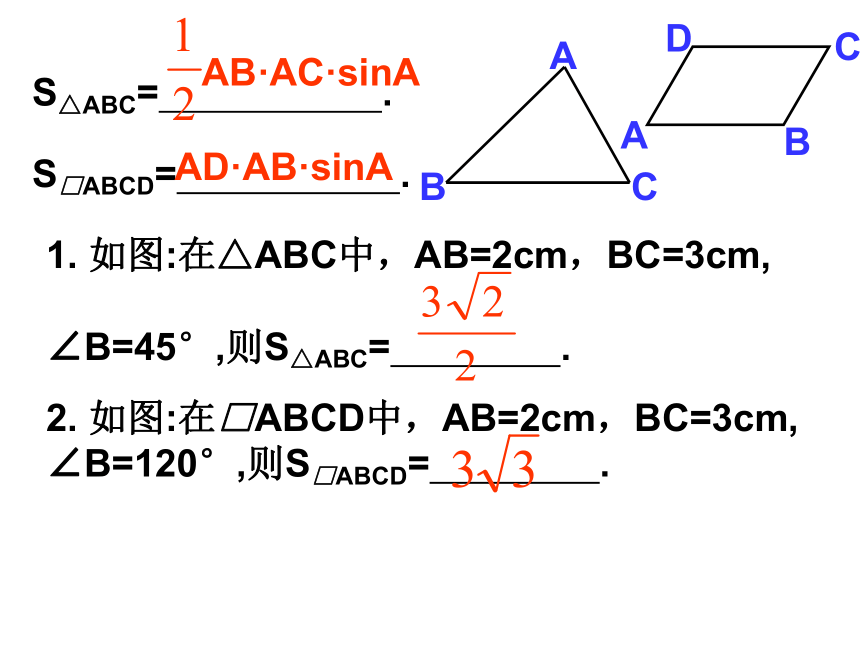
C45°练习一:CB0⑶ tan44°tan46°=( ).1(4)tan29°tan60°tan61°=( ).17.⑴ 已知:Rt△ABC中,∠C=90°∠A为锐角,且tanA=0.6,tanB=( ).⑵ sin2A+tanAtanB -2+cos2A=( )(5) sin53°cos37°+cos53°sin37°=( )S△ABC= .S□ABCD= .AD·AB·sinA1. 如图:在△ABC中,AB=2cm,BC=3cm,
∠B=45°,则S△ABC= .2. 如图:在□ABCD中,AB=2cm,BC=3cm,
∠B=120°,则S□ABCD= .练习二:1. 在△ABC中∠C=90° ∠B=2∠A 则cosA=____3.已A是锐角且tanA=3,则2. 若tan(β+20°)= , β为锐角 则β=________在Rt△ABC中,∠C=90°cosB= ,
则sinB的值为_______40° 5.如图所示,CD是平面镜,光线从A点出发经CD上点E反射后照射到B点。若入射角为α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=11,则tanα的值为 ( ) D6.已知sinθ=0.82904,
求∠θ的大小(精确到1′).8.一梯子斜靠在一面墙上,已知梯子长4m,梯子位于地面上的一端离墙壁2.5m,求梯子与地面所成的锐角. (精确到1′)7.已知cosθ=0.4,
求sinθ,tanθ的大小.例3、Rt△BAC中,∠ACB=900,sinB= D是BC上一点,DE⊥AB于E,CD=DE,AC+CD=9,分别求BC、DE的长,1.Rt△ABC中,a=2,c=5,则cos A=( ) C 2.思考: 求tan22.5°的值。练习三:3.如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.4.如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.锐角三角函数的应用D5 如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.6 如图,根据图中已知数据,求AD.随堂练习D 悟性的高低取决于有无悟“心”,其实,人与人的差别就在于你是否去思考,去发现.
cosA=sin(90°- A)=sinB1. 与cos70°值相等的是( )
(A)sin70° (B)cos20°(C)sin20°(D)tan70°
2.如图,在一次龙卷风中一棵大树在离地面若干
米处折断倒下,B为折断处最高点,树顶A落在离
树根C的12m处,测得∠BAC=30°,则BC的长是 m
3.若∠A为锐角,且tan2A+2tanA-3=0,则∠A= .
C45°练习一:CB0⑶ tan44°tan46°=( ).1(4)tan29°tan60°tan61°=( ).17.⑴ 已知:Rt△ABC中,∠C=90°∠A为锐角,且tanA=0.6,tanB=( ).⑵ sin2A+tanAtanB -2+cos2A=( )(5) sin53°cos37°+cos53°sin37°=( )S△ABC= .S□ABCD= .AD·AB·sinA1. 如图:在△ABC中,AB=2cm,BC=3cm,
∠B=45°,则S△ABC= .2. 如图:在□ABCD中,AB=2cm,BC=3cm,
∠B=120°,则S□ABCD= .练习二:1. 在△ABC中∠C=90° ∠B=2∠A 则cosA=____3.已A是锐角且tanA=3,则2. 若tan(β+20°)= , β为锐角 则β=________在Rt△ABC中,∠C=90°cosB= ,
则sinB的值为_______40° 5.如图所示,CD是平面镜,光线从A点出发经CD上点E反射后照射到B点。若入射角为α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=11,则tanα的值为 ( ) D6.已知sinθ=0.82904,
求∠θ的大小(精确到1′).8.一梯子斜靠在一面墙上,已知梯子长4m,梯子位于地面上的一端离墙壁2.5m,求梯子与地面所成的锐角. (精确到1′)7.已知cosθ=0.4,
求sinθ,tanθ的大小.例3、Rt△BAC中,∠ACB=900,sinB= D是BC上一点,DE⊥AB于E,CD=DE,AC+CD=9,分别求BC、DE的长,1.Rt△ABC中,a=2,c=5,则cos A=( ) C 2.思考: 求tan22.5°的值。练习三:3.如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.4.如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.锐角三角函数的应用D5 如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.6 如图,根据图中已知数据,求AD.随堂练习D 悟性的高低取决于有无悟“心”,其实,人与人的差别就在于你是否去思考,去发现.
