人教版七年级数学下册第五章《相交线与平行线》单元综合练习(含答案)
文档属性
| 名称 | 人教版七年级数学下册第五章《相交线与平行线》单元综合练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 153.5KB | ||
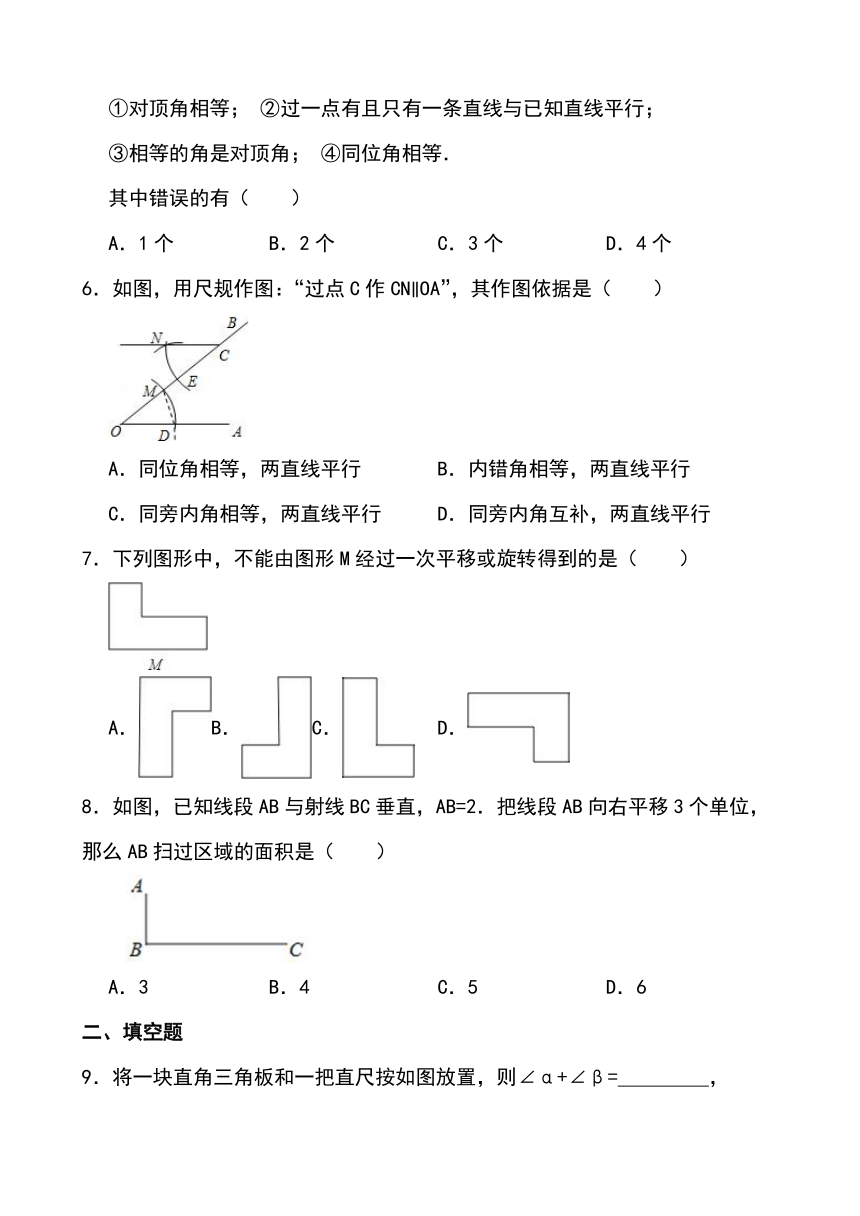
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-27 13:28:17 | ||
图片预览

文档简介
第五章《相交线与平行线》章节综合练习
一、选择题
1.对于直线AB,线段CD,射线EF,在下列各图中能相交的是( )
A. B.
C. D.
2.如图:不能推出的条件是( )
A. B.
C. D.
3.已知点P为直线m外一点,点A,B,C为直线m上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线m的距离为( )
A.4 cm B.5 cm C.小于2 cm D.不大于2 cm
4.如图所示,下列说法正确的是( )
A.∠1和∠2是内错角 B.∠1和∠5是同位角
C.∠1和∠2是同旁内角 D.∠1和∠4是内错角
5.命题:
①对顶角相等; ②过一点有且只有一条直线与已知直线平行;
③相等的角是对顶角; ④同位角相等.
其中错误的有( )
A.1个 B.2个 C.3个 D.4个
6.如图,用尺规作图:“过点C作CNOA”,其作图依据是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角相等,两直线平行 D.同旁内角互补,两直线平行
7.下列图形中,不能由图形M经过一次平移或旋转得到的是( )
A.B.C. D.
8.如图,已知线段AB与射线BC垂直,AB=2.把线段AB向右平移3个单位,那么AB扫过区域的面积是( )
A.3 B.4 C.5 D.6
二、填空题
9.将一块直角三角板和一把直尺按如图放置,则∠α+∠β= ,
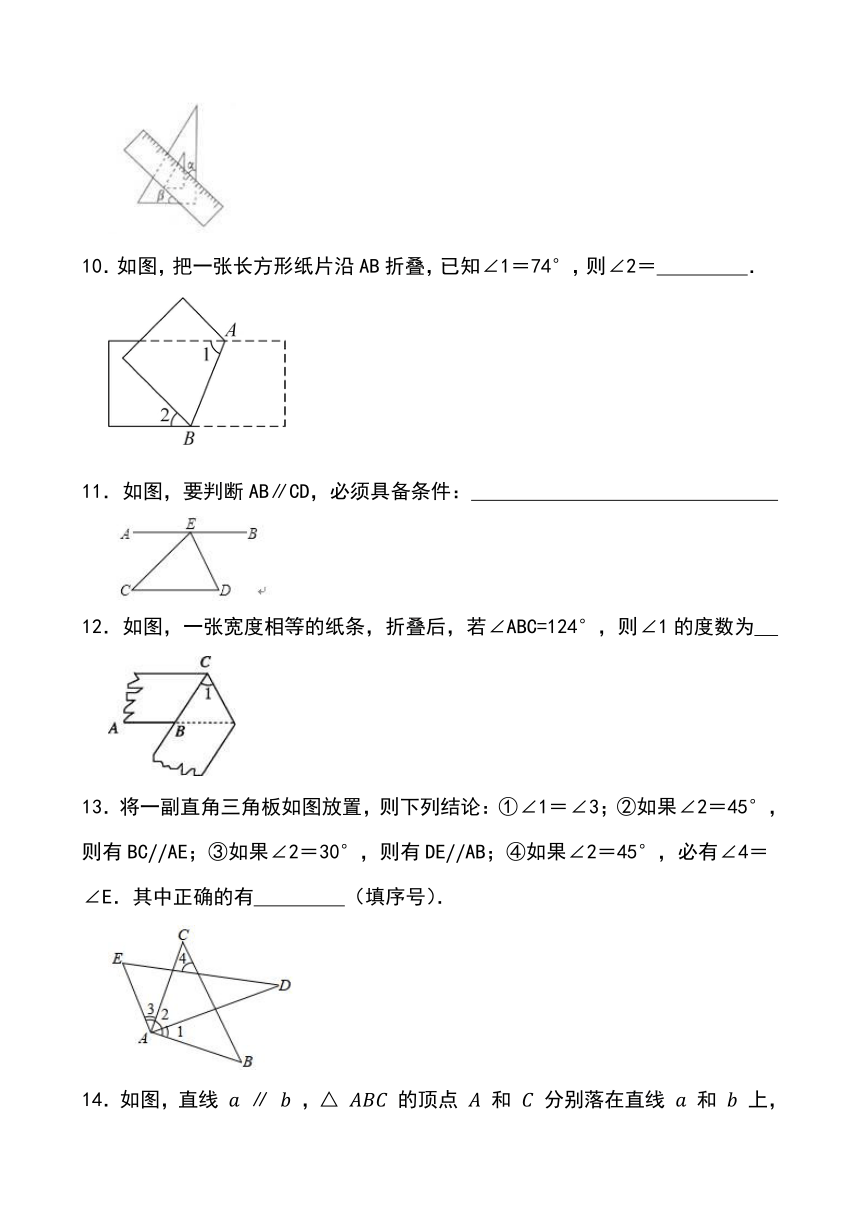
10.如图,把一张长方形纸片沿AB折叠,已知∠1=74°,则∠2= .
11.如图,要判断AB∥CD,必须具备条件:
12.如图,一张宽度相等的纸条,折叠后,若∠ABC=124°,则∠1的度数为
13.将一副直角三角板如图放置,则下列结论:①∠1=∠3;②如果∠2=45°,则有BCAE;③如果∠2=30°,则有DEAB;④如果∠2=45°,必有∠4=∠E.其中正确的有 (填序号).
14.如图,直线 ∥ ,△ 的顶点 和 分别落在直线 和 上,若∠1=60°,且∠1+∠2=90°,则 的度数是 °.
15.如图所示,直线CD、EF被直线AB所截,若∠AMC=∠BNF,则∠CMN+∠MNE= °.
16.如图,将△ABC水平向右平移了acm后,得到△A'B'C',已知BC=6cm,B C'=17cm,那么a= cm.
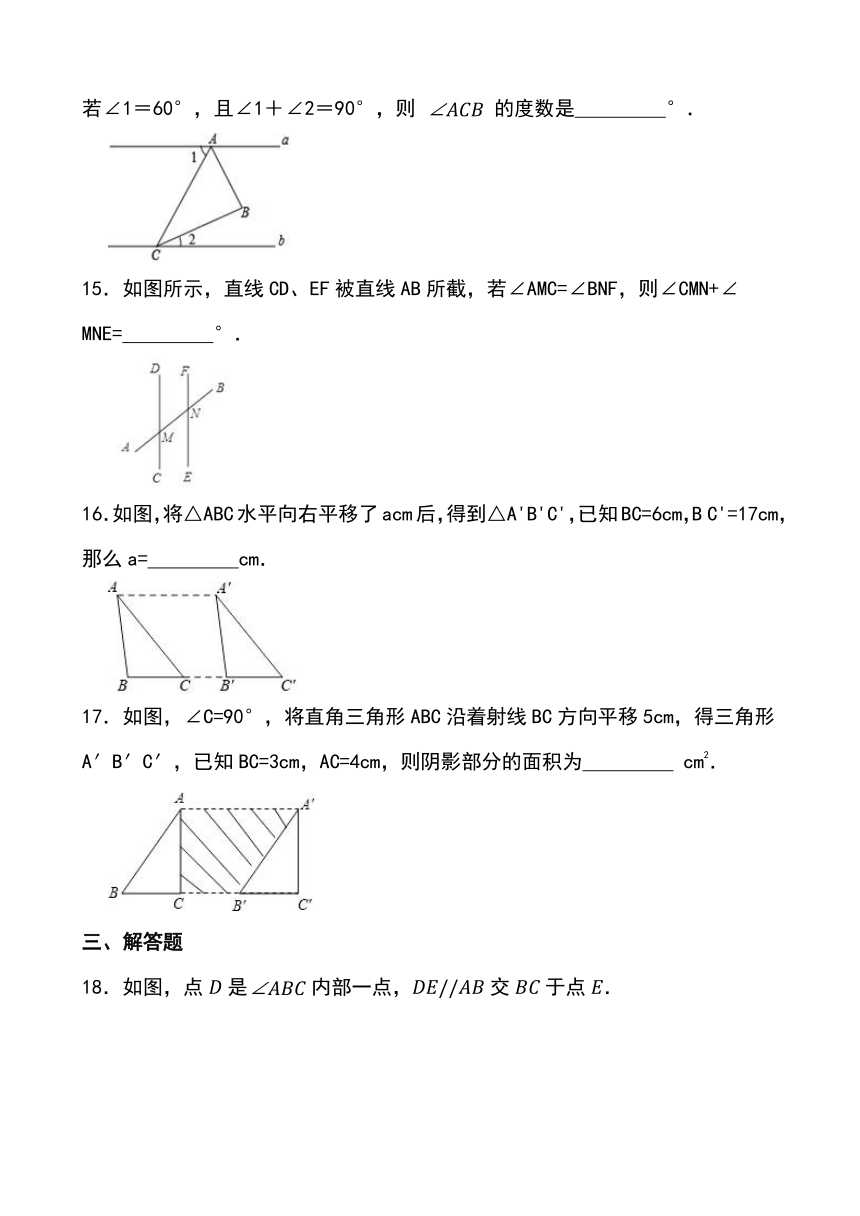
17.如图,∠C=90°,将直角三角形ABC沿着射线BC方向平移5cm,得三角形A′B′C′,已知BC=3cm,AC=4cm,则阴影部分的面积为 cm2.
三、解答题
18.如图,点是内部一点,交于点.
(1)请尺规作图:画出射线,使得,交直线于点;
(2)请你直接写出与的数量关系: .
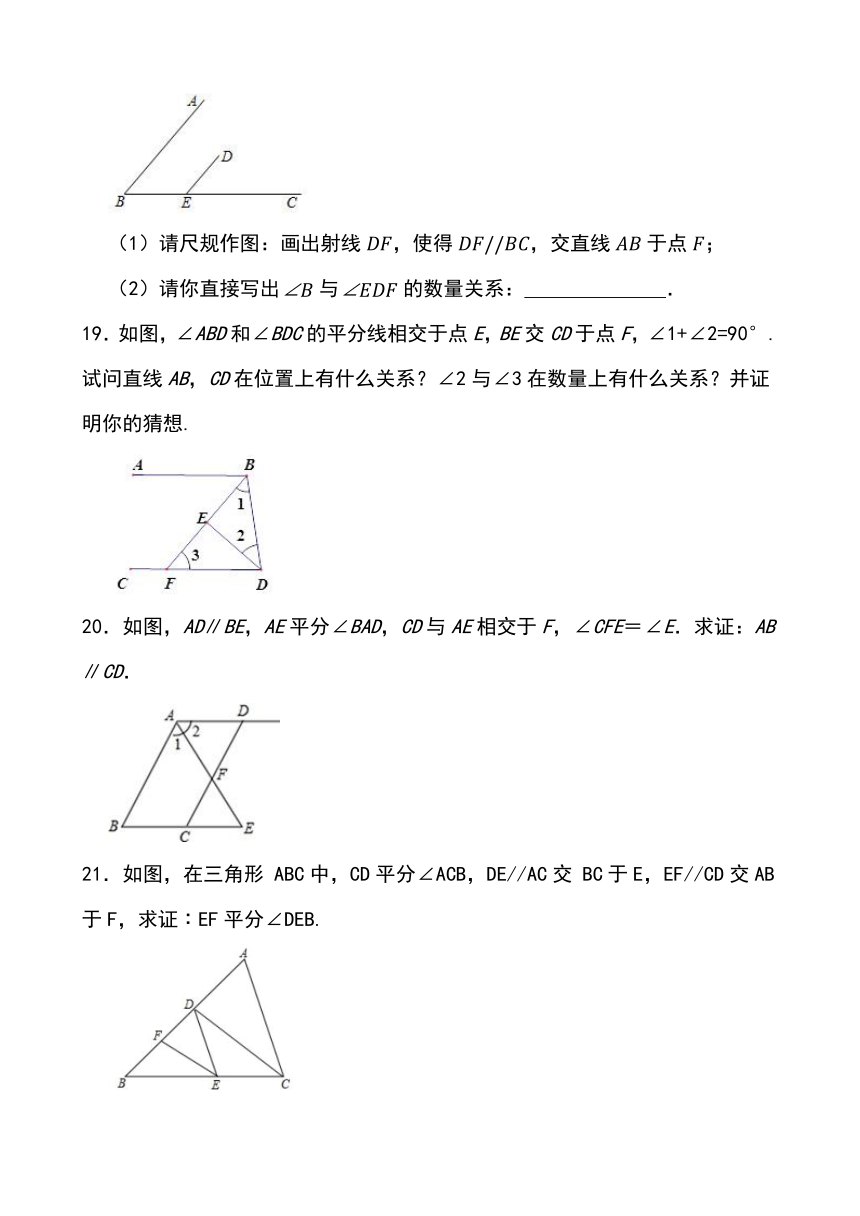
19.如图,∠ABD和∠BDC的平分线相交于点E,BE交CD于点F,∠1+∠2=90°.试问直线AB,CD在位置上有什么关系?∠2与∠3在数量上有什么关系?并证明你的猜想.
20.如图,AD∥BE,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AB∥CD.
21.如图,在三角形 ABC中,CD平分∠ACB,DE//AC交 BC于E,EF//CD交AB于F,求证∶EF平分∠DEB.
22.如图,已知,.
(1)求证:;
(2)若,平分,求的度数.
23.已知大正方形的边长为4cm,小正方形的边.长为2cm,起始状态如图所示.大正方形固定不动,把小正方形以1cm/s的速度沿水平方向向右平移,设平移的时间为1(s).两个正方形重叠部分的面积为S(cm2).完成下列问题:
(1)平移1.5s时,S= cm2
(2)当2≤t≤4时,小正方形的一条对角线扫过图形的面积为多少?
(3)当S=2cm2时,小正方形平移的距离为多少厘米?
答案解析部分
1.B
2.C
3.D
4.C
5.C
6.B
7.C
8.D
9.90°
10.32°
11.∠AEC=∠C或∠BED=∠D或∠C+∠CEB=180°或∠D+∠AED=180°
12.62°
13.①②④
14.30
15.180
16.11
17.14
18.(1)解:如图,射线即为所求.
(2)
19.解:AB∥CD,∠2与∠3互余.理由如下:∵BE,DE平分∠ABD,∠CDB.∴∠1= ∠ABD,∠2= ∠CDB.∴∠1+∠2= (∠ABD+∠CDB).∵∠1+∠2=90°.∴∠ABD+∠CDB=180°.∴AB∥CD.∴∠ABF=∠3.∵∠1=∠ABF.∴∠1=∠3.∵∠1+∠2=90°.∴∠2+∠3=90°.∴∠2与∠3互余.
20.解:
(两直线平行,内错角相等)
平分
又
.(同位角相等,两直线平行)
21.证明:CD平分∠ACB,
∴∠ACD=∠DCB,
∵DE//AC,EF//CD,
∴∠ACD=∠EDC,∠FED=∠EDC,∠BEF=∠DCB
∴∠ACD=∠FED=∠DCB=∠BEF,
∴EF平分∠DEB.
22.(1)证明:∵,,
∴,
∴
(2)解:∵,
∴,
∵,
∴,
∴,
∴,
∵平分,
∴,
∵,,
∴.
23.(1)3
(2)解:如图,当2≤t≤4时,小正方形的一条对角线扫过图形为图中的平行四边形,
∴S=2×2=4cm2;
(3)解:当S=2cm2时,重叠部分的宽为2÷2=1cm,
①如图,小正方形平移的距离为1Cm;
②如图,小正方形平移的距离为4-1+2=5cm,
综上所述,小正方形平移的距离为1cm或5cm.
一、选择题
1.对于直线AB,线段CD,射线EF,在下列各图中能相交的是( )
A. B.
C. D.
2.如图:不能推出的条件是( )
A. B.
C. D.
3.已知点P为直线m外一点,点A,B,C为直线m上三点,PA=4 cm,PB=5 cm,PC=2 cm,则点P到直线m的距离为( )
A.4 cm B.5 cm C.小于2 cm D.不大于2 cm
4.如图所示,下列说法正确的是( )
A.∠1和∠2是内错角 B.∠1和∠5是同位角
C.∠1和∠2是同旁内角 D.∠1和∠4是内错角
5.命题:
①对顶角相等; ②过一点有且只有一条直线与已知直线平行;
③相等的角是对顶角; ④同位角相等.
其中错误的有( )
A.1个 B.2个 C.3个 D.4个
6.如图,用尺规作图:“过点C作CNOA”,其作图依据是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角相等,两直线平行 D.同旁内角互补,两直线平行
7.下列图形中,不能由图形M经过一次平移或旋转得到的是( )
A.B.C. D.
8.如图,已知线段AB与射线BC垂直,AB=2.把线段AB向右平移3个单位,那么AB扫过区域的面积是( )
A.3 B.4 C.5 D.6
二、填空题
9.将一块直角三角板和一把直尺按如图放置,则∠α+∠β= ,
10.如图,把一张长方形纸片沿AB折叠,已知∠1=74°,则∠2= .
11.如图,要判断AB∥CD,必须具备条件:
12.如图,一张宽度相等的纸条,折叠后,若∠ABC=124°,则∠1的度数为
13.将一副直角三角板如图放置,则下列结论:①∠1=∠3;②如果∠2=45°,则有BCAE;③如果∠2=30°,则有DEAB;④如果∠2=45°,必有∠4=∠E.其中正确的有 (填序号).
14.如图,直线 ∥ ,△ 的顶点 和 分别落在直线 和 上,若∠1=60°,且∠1+∠2=90°,则 的度数是 °.
15.如图所示,直线CD、EF被直线AB所截,若∠AMC=∠BNF,则∠CMN+∠MNE= °.
16.如图,将△ABC水平向右平移了acm后,得到△A'B'C',已知BC=6cm,B C'=17cm,那么a= cm.
17.如图,∠C=90°,将直角三角形ABC沿着射线BC方向平移5cm,得三角形A′B′C′,已知BC=3cm,AC=4cm,则阴影部分的面积为 cm2.
三、解答题
18.如图,点是内部一点,交于点.
(1)请尺规作图:画出射线,使得,交直线于点;
(2)请你直接写出与的数量关系: .
19.如图,∠ABD和∠BDC的平分线相交于点E,BE交CD于点F,∠1+∠2=90°.试问直线AB,CD在位置上有什么关系?∠2与∠3在数量上有什么关系?并证明你的猜想.
20.如图,AD∥BE,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AB∥CD.
21.如图,在三角形 ABC中,CD平分∠ACB,DE//AC交 BC于E,EF//CD交AB于F,求证∶EF平分∠DEB.
22.如图,已知,.
(1)求证:;
(2)若,平分,求的度数.
23.已知大正方形的边长为4cm,小正方形的边.长为2cm,起始状态如图所示.大正方形固定不动,把小正方形以1cm/s的速度沿水平方向向右平移,设平移的时间为1(s).两个正方形重叠部分的面积为S(cm2).完成下列问题:
(1)平移1.5s时,S= cm2
(2)当2≤t≤4时,小正方形的一条对角线扫过图形的面积为多少?
(3)当S=2cm2时,小正方形平移的距离为多少厘米?
答案解析部分
1.B
2.C
3.D
4.C
5.C
6.B
7.C
8.D
9.90°
10.32°
11.∠AEC=∠C或∠BED=∠D或∠C+∠CEB=180°或∠D+∠AED=180°
12.62°
13.①②④
14.30
15.180
16.11
17.14
18.(1)解:如图,射线即为所求.
(2)
19.解:AB∥CD,∠2与∠3互余.理由如下:∵BE,DE平分∠ABD,∠CDB.∴∠1= ∠ABD,∠2= ∠CDB.∴∠1+∠2= (∠ABD+∠CDB).∵∠1+∠2=90°.∴∠ABD+∠CDB=180°.∴AB∥CD.∴∠ABF=∠3.∵∠1=∠ABF.∴∠1=∠3.∵∠1+∠2=90°.∴∠2+∠3=90°.∴∠2与∠3互余.
20.解:
(两直线平行,内错角相等)
平分
又
.(同位角相等,两直线平行)
21.证明:CD平分∠ACB,
∴∠ACD=∠DCB,
∵DE//AC,EF//CD,
∴∠ACD=∠EDC,∠FED=∠EDC,∠BEF=∠DCB
∴∠ACD=∠FED=∠DCB=∠BEF,
∴EF平分∠DEB.
22.(1)证明:∵,,
∴,
∴
(2)解:∵,
∴,
∵,
∴,
∴,
∴,
∵平分,
∴,
∵,,
∴.
23.(1)3
(2)解:如图,当2≤t≤4时,小正方形的一条对角线扫过图形为图中的平行四边形,
∴S=2×2=4cm2;
(3)解:当S=2cm2时,重叠部分的宽为2÷2=1cm,
①如图,小正方形平移的距离为1Cm;
②如图,小正方形平移的距离为4-1+2=5cm,
综上所述,小正方形平移的距离为1cm或5cm.
