新课标人教A版选修4-1《几何证明选讲》综合复习(全解析)
文档属性
| 名称 | 新课标人教A版选修4-1《几何证明选讲》综合复习(全解析) |

|
|
| 格式 | rar | ||
| 文件大小 | 386.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-02-19 00:00:00 | ||
图片预览


文档简介
人教(A)版选修4-1《几何证明选讲》综合复习
钱耀周
(广东佛山市南海区南海中学,528211)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图4所示,圆O的直径AB=6,C为圆周上一点,BC=3过C作
圆的切线l,过A作l的垂线AD,垂足为D,则∠DAC =( )
A. B. C. D.
【解析】由弦切角定理得,又,故,
故选B.
2.在中,、分别是斜边上的高和中线,是该图中共有个三角形与相似,则( )
A.0 B.1 C.2 D.3
【解析】2个:和,故选C.
3.一个圆的两弦相交,一条弦被分为12和18两段,另一弦被分为,则另一弦的长为( )
A. B. C. D.
【解析】设另一弦被分的两段长分别为,由相交弦定理得,解得,故所求弦长为.故选B.
4.如图,在和中,,若与
的周长之差为,则的周长为( )
A. B. C. D.25
【解析】利用相似三角形的相似比等于周长比可得答案D.
5.的割线交于两点,割线经过圆心,已知,则的半径为( )
A.4 B. C. D.8
【解析】设半径为,由割线定理有,解得.故选D.
6.如图,是半圆的直径,点在半圆上,于点,
且,设,则=( )
A. B. C. D.
【解析】设半径为,则,由得,从而,故,选A.
7.在中,分别为上的点,且,的面积是,梯形的面积为,则的值为( )
A. B. C. D.
【解析】,利用面积比等于相似比的平方可得答案B.
8.半径分别为1和2的两圆外切,作半径为3的圆与这两圆均相切,一共可作( )个.
A.2 B.3 C.4 D.5
【解析】一共可作5个,其中均外切的2个,均内切的1个,一外切一内切的2个,故选D.
9.如图甲,四边形是等腰梯形,.由4个这样的
等腰梯形可以拼出图乙所示的平行四边形,
则四边形中度数为 ( )
A. B. C. D.
【解析】,从而,选A.
10.如图,为测量金属材料的硬度,用一定压力把一个高强度钢珠
压向该种材料的表面,在材料表面留下一个凹坑,现测得凹坑
直径为10mm,若所用钢珠的直径为26 mm,则凹坑深度为( )
A.1mm B.2 mm C.3mm D.4 mm
【解析】依题意得,从而,
故,选A.
11.如图,设为内的两点,且,=+,则的面积与的面积之比为( )
A. B. C. D.
【解析】如图,设,,则.
由平行四边形法则知,所以=,
同理可得.故,选B.
12.如图,用与底面成角的平面截圆柱得一椭圆截线,则该椭圆的
离心率为 ( )
A. B. C. D.非上述结论
【解析】用平面截圆柱,截线椭圆的短轴长为圆柱截面圆的直径,弄清了这一概念,考虑椭圆所在平面与底面成角,则离心率.故选A.
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
13.一平面截球面产生的截面形状是_______;它截圆柱面所产生的截面形状是________
【解析】圆;圆或椭圆.
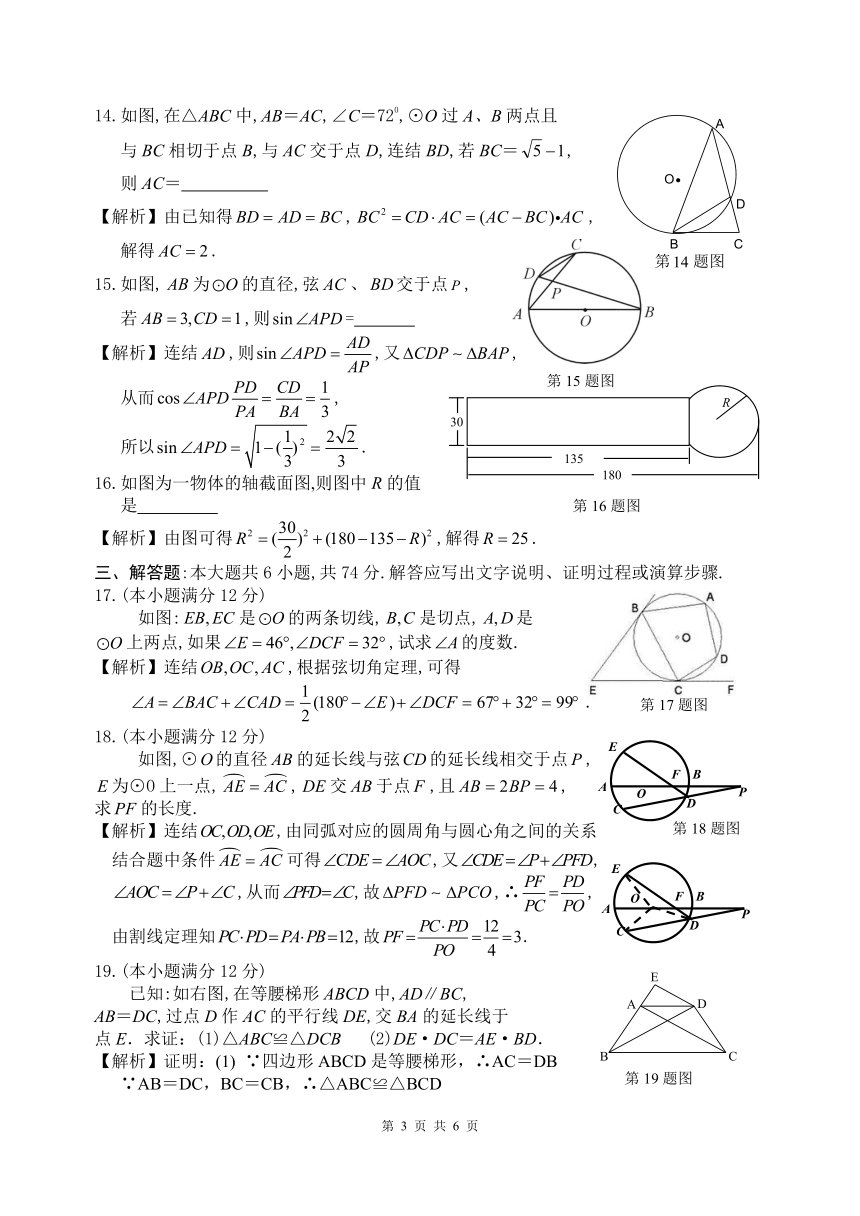
14.如图,在△ABC中,AB=AC,∠C=720,⊙O过A、B两点且
与BC相切于点B,与AC交于点D,连结BD,若BC=,
则AC=
【解析】由已知得,,
解得.
15.如图,为的直径,弦、交于点,
若,则=
【解析】连结,则,又,
从而,
所以.
16.如图为一物体的轴截面图,则图中R的值
是
【解析】由图可得,解得.
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
如图:是的两条切线,是切点,是
上两点,如果,试求的度数.
【解析】连结,根据弦切角定理,可得
.
18.(本小题满分12分)
如图,⊙的直径的延长线与弦的延长线相交于点,
为⊙O上一点,,交于点,且,
求的长度.
【解析】连结,由同弧对应的圆周角与圆心角之间的关系
结合题中条件可得,又,
,从而,故,∴,
由割线定理知,故.
19.(本小题满分12分)
已知:如右图,在等腰梯形ABCD中,AD∥BC,
AB=DC,过点D作AC的平行线DE,交BA的延长线于
点E.求证:(1)△ABC≌△DCB (2)DE·DC=AE·BD.
【解析】证明:(1) ∵四边形ABCD是等腰梯形,∴AC=DB
∵AB=DC,BC=CB,∴△ABC≌△BCD
(2)∵△ABC≌△BCD,∴∠ACB=∠DBC,∠ABC=∠DCB
∵AD∥BC,∴∠DAC=∠ACB,∠EAD=∠ABC
∵ED∥AC,∴∠EDA=∠DAC ∴∠EDA=∠DBC,∠EAD=∠DCB
∴△ADE∽△CBD ∴DE:BD=AE:CD, ∴DE·DC=AE·BD.
20.(本小题满分12分)
如图,△ABC中,AB=AC,AD是中线,P为AD上一点,CF∥AB,BP延长线交AC、CF于E、F,求证: PB=PE?PF.
【解析】连结,易证
∵ ∴,从而
又为与的公共角,
从而,∴ ∴
又, ∴,命题得证.
21.(本小题满分12分)
如图,是以为直径的上一点,于点,
过点作的切线,与的延长线相交于点是
的中点,连结并延长与相交于点,
延长与的延长线相交于点.
(1)求证:;
(2)求证:是的切线;
(3)若,且的半径长为,求和的长度.
【解析】(1)证明:是的直径,是的切线,
.又,.
易证,.
..
是的中点,..
(2)证明:连结.是的直径,.
在中,由(1),知是斜边的中点,
..又,.
是的切线,.
,是的切线.
(3)解:过点作于点.,.
由(1),知,.
由已知,有,,即是等腰三角形.
,.,,即.
,四边形是矩形,.
,易证.,即.
的半径长为,..
解得..,..
在中,,,由勾股定理,得.
.解得(负值舍去)..
[或取的中点,连结,则.易证,,故,.由,易知,.
由,解得.又在中,由勾股定理,得
,(舍去负值).]
22.(本小题满分14分)
如图1,点将线段分成两部分,如果,那么称点为线段的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线将一个面积为的图形分成两部分,这两部分的面积分别为,,如果,那么称直线为该图形的黄金分割线.
(1)研究小组猜想:在中,若点为边上的黄金分割点(如图2),则直线是的黄金分割线.你认为对吗?为什么?
(2)请你说明:三角形的中线是否也是该三角形的黄金分割线?
(3)研究小组在进一步探究中发现:过点任作一条直线交于点,再过点作直线,交于点,连接(如图3),则直线也是的黄金分割线.请你说明理由.
(4)如图4,点是的边的黄金分割点,过点作,交于点,显然直线是的黄金分割线.请你画一条的黄金分割线,使它不经过各边黄金分割点.
【解析】(1)直线是的黄金分割线.理由如下:设的边上的高为.
,,,所以,
又因为点为边的黄金分割点,所以有.因此.
所以,直线是的黄金分割线.
(2)因为三角形的中线将三角形分成面积相等的两部分,此时,即,所以三角形的中线不可能是该三角形的黄金分割线.
(3)因为,∴和的公共边上的高也相等,所以有
设直线与交于点.所以.所以
,.
又因为,所以.
因此,直线也是的黄金分割线.
(4)画法不惟一,现提供两种画法;
画法一:如答图1,取的中点,再过点作一条直线分别交,于,点,则直线就是的黄金分割线.
画法二:如答图2,在上取一点,连接,再过点作交于点,连接,则直线就是的黄金分割线.
钱耀周
(广东佛山市南海区南海中学,528211)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图4所示,圆O的直径AB=6,C为圆周上一点,BC=3过C作
圆的切线l,过A作l的垂线AD,垂足为D,则∠DAC =( )
A. B. C. D.
【解析】由弦切角定理得,又,故,
故选B.
2.在中,、分别是斜边上的高和中线,是该图中共有个三角形与相似,则( )
A.0 B.1 C.2 D.3
【解析】2个:和,故选C.
3.一个圆的两弦相交,一条弦被分为12和18两段,另一弦被分为,则另一弦的长为( )
A. B. C. D.
【解析】设另一弦被分的两段长分别为,由相交弦定理得,解得,故所求弦长为.故选B.
4.如图,在和中,,若与
的周长之差为,则的周长为( )
A. B. C. D.25
【解析】利用相似三角形的相似比等于周长比可得答案D.
5.的割线交于两点,割线经过圆心,已知,则的半径为( )
A.4 B. C. D.8
【解析】设半径为,由割线定理有,解得.故选D.
6.如图,是半圆的直径,点在半圆上,于点,
且,设,则=( )
A. B. C. D.
【解析】设半径为,则,由得,从而,故,选A.
7.在中,分别为上的点,且,的面积是,梯形的面积为,则的值为( )
A. B. C. D.
【解析】,利用面积比等于相似比的平方可得答案B.
8.半径分别为1和2的两圆外切,作半径为3的圆与这两圆均相切,一共可作( )个.
A.2 B.3 C.4 D.5
【解析】一共可作5个,其中均外切的2个,均内切的1个,一外切一内切的2个,故选D.
9.如图甲,四边形是等腰梯形,.由4个这样的
等腰梯形可以拼出图乙所示的平行四边形,
则四边形中度数为 ( )
A. B. C. D.
【解析】,从而,选A.
10.如图,为测量金属材料的硬度,用一定压力把一个高强度钢珠
压向该种材料的表面,在材料表面留下一个凹坑,现测得凹坑
直径为10mm,若所用钢珠的直径为26 mm,则凹坑深度为( )
A.1mm B.2 mm C.3mm D.4 mm
【解析】依题意得,从而,
故,选A.
11.如图,设为内的两点,且,=+,则的面积与的面积之比为( )
A. B. C. D.
【解析】如图,设,,则.
由平行四边形法则知,所以=,
同理可得.故,选B.
12.如图,用与底面成角的平面截圆柱得一椭圆截线,则该椭圆的
离心率为 ( )
A. B. C. D.非上述结论
【解析】用平面截圆柱,截线椭圆的短轴长为圆柱截面圆的直径,弄清了这一概念,考虑椭圆所在平面与底面成角,则离心率.故选A.
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
13.一平面截球面产生的截面形状是_______;它截圆柱面所产生的截面形状是________
【解析】圆;圆或椭圆.
14.如图,在△ABC中,AB=AC,∠C=720,⊙O过A、B两点且
与BC相切于点B,与AC交于点D,连结BD,若BC=,
则AC=
【解析】由已知得,,
解得.
15.如图,为的直径,弦、交于点,
若,则=
【解析】连结,则,又,
从而,
所以.
16.如图为一物体的轴截面图,则图中R的值
是
【解析】由图可得,解得.
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
如图:是的两条切线,是切点,是
上两点,如果,试求的度数.
【解析】连结,根据弦切角定理,可得
.
18.(本小题满分12分)
如图,⊙的直径的延长线与弦的延长线相交于点,
为⊙O上一点,,交于点,且,
求的长度.
【解析】连结,由同弧对应的圆周角与圆心角之间的关系
结合题中条件可得,又,
,从而,故,∴,
由割线定理知,故.
19.(本小题满分12分)
已知:如右图,在等腰梯形ABCD中,AD∥BC,
AB=DC,过点D作AC的平行线DE,交BA的延长线于
点E.求证:(1)△ABC≌△DCB (2)DE·DC=AE·BD.
【解析】证明:(1) ∵四边形ABCD是等腰梯形,∴AC=DB
∵AB=DC,BC=CB,∴△ABC≌△BCD
(2)∵△ABC≌△BCD,∴∠ACB=∠DBC,∠ABC=∠DCB
∵AD∥BC,∴∠DAC=∠ACB,∠EAD=∠ABC
∵ED∥AC,∴∠EDA=∠DAC ∴∠EDA=∠DBC,∠EAD=∠DCB
∴△ADE∽△CBD ∴DE:BD=AE:CD, ∴DE·DC=AE·BD.
20.(本小题满分12分)
如图,△ABC中,AB=AC,AD是中线,P为AD上一点,CF∥AB,BP延长线交AC、CF于E、F,求证: PB=PE?PF.
【解析】连结,易证
∵ ∴,从而
又为与的公共角,
从而,∴ ∴
又, ∴,命题得证.
21.(本小题满分12分)
如图,是以为直径的上一点,于点,
过点作的切线,与的延长线相交于点是
的中点,连结并延长与相交于点,
延长与的延长线相交于点.
(1)求证:;
(2)求证:是的切线;
(3)若,且的半径长为,求和的长度.
【解析】(1)证明:是的直径,是的切线,
.又,.
易证,.
..
是的中点,..
(2)证明:连结.是的直径,.
在中,由(1),知是斜边的中点,
..又,.
是的切线,.
,是的切线.
(3)解:过点作于点.,.
由(1),知,.
由已知,有,,即是等腰三角形.
,.,,即.
,四边形是矩形,.
,易证.,即.
的半径长为,..
解得..,..
在中,,,由勾股定理,得.
.解得(负值舍去)..
[或取的中点,连结,则.易证,,故,.由,易知,.
由,解得.又在中,由勾股定理,得
,(舍去负值).]
22.(本小题满分14分)
如图1,点将线段分成两部分,如果,那么称点为线段的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线将一个面积为的图形分成两部分,这两部分的面积分别为,,如果,那么称直线为该图形的黄金分割线.
(1)研究小组猜想:在中,若点为边上的黄金分割点(如图2),则直线是的黄金分割线.你认为对吗?为什么?
(2)请你说明:三角形的中线是否也是该三角形的黄金分割线?
(3)研究小组在进一步探究中发现:过点任作一条直线交于点,再过点作直线,交于点,连接(如图3),则直线也是的黄金分割线.请你说明理由.
(4)如图4,点是的边的黄金分割点,过点作,交于点,显然直线是的黄金分割线.请你画一条的黄金分割线,使它不经过各边黄金分割点.
【解析】(1)直线是的黄金分割线.理由如下:设的边上的高为.
,,,所以,
又因为点为边的黄金分割点,所以有.因此.
所以,直线是的黄金分割线.
(2)因为三角形的中线将三角形分成面积相等的两部分,此时,即,所以三角形的中线不可能是该三角形的黄金分割线.
(3)因为,∴和的公共边上的高也相等,所以有
设直线与交于点.所以.所以
,.
又因为,所以.
因此,直线也是的黄金分割线.
(4)画法不惟一,现提供两种画法;
画法一:如答图1,取的中点,再过点作一条直线分别交,于,点,则直线就是的黄金分割线.
画法二:如答图2,在上取一点,连接,再过点作交于点,连接,则直线就是的黄金分割线.
