人教A版(2019)必修二 第八章 立体几何初步 章节测试题(含解析)
文档属性
| 名称 | 人教A版(2019)必修二 第八章 立体几何初步 章节测试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-26 00:00:00 | ||
图片预览



文档简介
人教A版(2019)必修二 第八章 立体几何初步 章节测试题
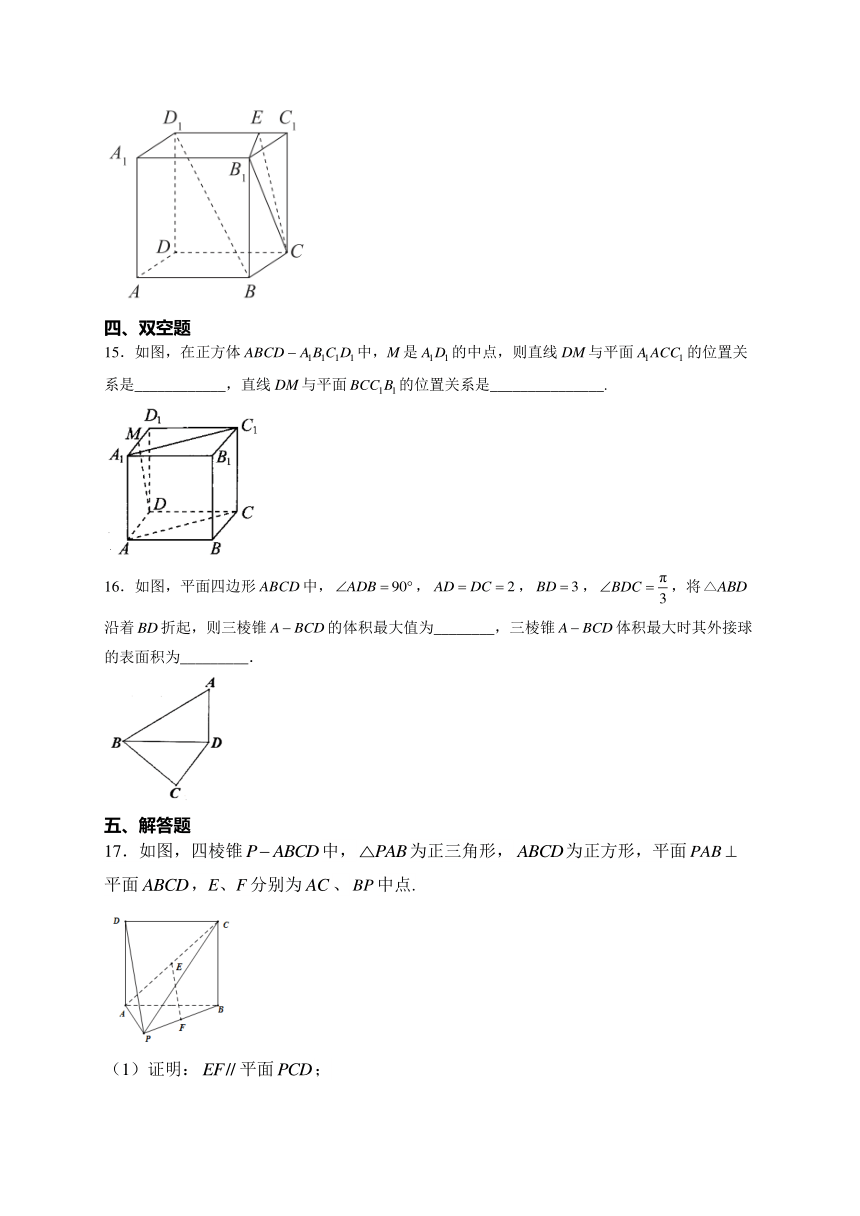
学校:___________姓名:___________班级:___________考号:___________
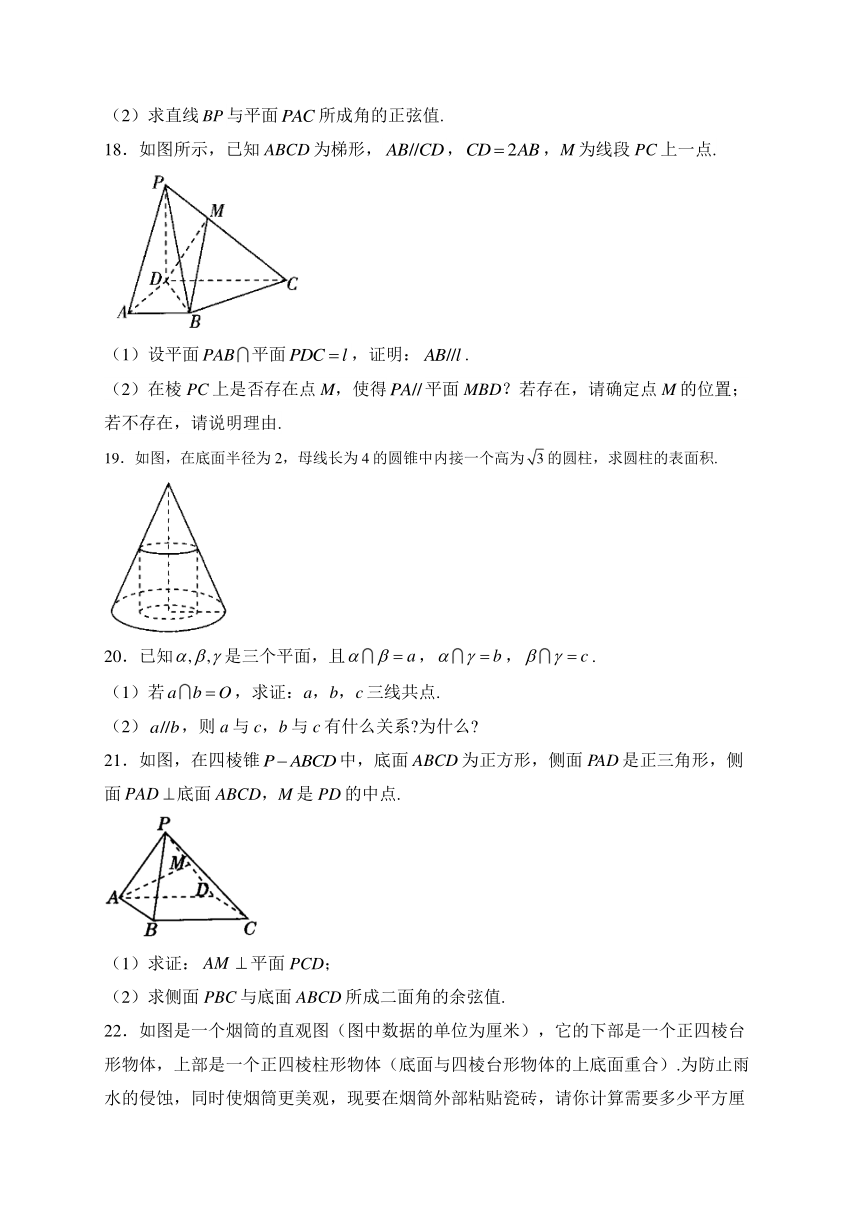
一、选择题
1.已知正方体的外接球表面积为,点E为棱的中点,且平面,点平面,则平面截正方体所得的截面图形的面积为( )
A. B. C. D.
2.如图所示,已知正方形的边长为1,它是水平放置的一个平面图形的直观图,则其原图形的面积为( )
A.1 B. C. D.8
3.已知正方形OABC的边长为2,它的水平放置的一个平面图形的直观图为(在轴上),则图形的面积是( )
A.4 B.2 C. D.1
4.在底面半径为1的圆锥中,若该圆锥侧面展开图的面积是,则该圆锥的体积为( )
A. B. C. D.
5.水平放置的的直观图如图所示,是中边的中点,且平行于轴,则,,对应于原中的线段AB,AD,AC,对于这三条线段,正确的判断是( )
A.最短的是AD B.最短的是AC C. D.
6.我们知道立体图形上的最短路径问题通常是把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.请根据此方法求函数的最小值( )
A. B. C. D.
7.已知在直三棱柱中,E,F分别为,的中点,,,,,如图所示,若过A,E,F三点的平面作该直三棱柱的截面,则所得截面的面积为( )
A. B. C. D.
8.已知某圆台的高为,上底面半径为1,下底面半径为2,则其侧面展开图的面积为( )
A.9π B. C. D.
二、多项选择题
9.已知AC为圆锥SO底面圆O的直径(S为顶点,O为圆心),点B为圆O上异于A,C的动点,,则下列结论正确的为( )
A. 圆锥SO的侧面积为
B.的取值范围为
C.若,E为线段AB上的动点,则
D. 过该圆锥顶点S的平面截此圆锥所得截面面积的最大值为
10.如图所示的是水平放置的三角形直观图,是中边上的一点,且,又轴,那么原的AB、AD、AC三条线段中( )
A.最长的是AB B.最长的是AC
C.最短的是AC D.最短的是AD
11.如图,正方体中,O为底面ABCD的中心,M为棱的中点,则下列结论中正确的是( )
A.平面
B.平面MAC
C.异面直线与AC所成的角为60°
D.平面ABCD
12.已知的三边长分别为,,,M是AB边上的点,P是平面ABC外一点.给出下列四个命题,其中是真命题的有( )
A.若平面ABC,则三棱锥的四个面都是直角三角形
B.若平面ABC,且M是AB边的中点,则
C.若,平面ABC,则面积的最小值为
D.若,P在平面ABC内的射影是内切圆的圆心,则点P到平面ABC的距离为
三、填空题
13.在棱长为1的正方体中,E为的中点,则点到直线CE的距离为______.
14.如图,E是正方体的棱上一点,直线平面,则异面直线与CE所成的角的余弦值为__________.
四、双空题
15.如图,在正方体中,M是的中点,则直线DM与平面的位置关系是____________,直线DM与平面的位置关系是_______________.
16.如图,平面四边形中,,,,,将沿着折起,则三棱锥的体积最大值为________,三棱锥体积最大时其外接球的表面积为_________.
五、解答题
17.如图,四棱锥中,为正三角形,为正方形,平面平面,E、F分别为、中点.
(1)证明:平面;
(2)求直线与平面所成角的正弦值.
18.如图所示,已知ABCD为梯形,,,M为线段PC上一点.
(1)设平面平面,证明:.
(2)在棱PC上是否存在点M,使得平面MBD?若存在,请确定点M的位置;若不存在,请说明理由.
19.如图,在底面半径为2,母线长为4的圆锥中内接一个高为的圆柱,求圆柱的表面积.
20.已知是三个平面,且,,.
(1)若,求证:a,b,c三线共点.
(2),则a与c,b与c有什么关系 为什么
21.如图,在四棱锥中,底面ABCD为正方形,侧面PAD是正三角形,侧面底面ABCD,M是PD的中点.
(1)求证:平面PCD;
(2)求侧面PBC与底面ABCD所成二面角的余弦值.
22.如图是一个烟筒的直观图(图中数据的单位为厘米),它的下部是一个正四棱台形物体,上部是一个正四棱柱形物体(底面与四棱台形物体的上底面重合).为防止雨水的侵蚀,同时使烟筒更美观,现要在烟筒外部粘贴瓷砖,请你计算需要多少平方厘米的瓷砖?(结果精确到,可用计算工具)
参考答案
1.答案:D
解析:设该正方体外接球的半径为R,依题意,,解得,故,则,解得.
分别取棱AB,BC的中点F,G,连接,,,,
根据正方体的性质可知:四边形为等腰梯形,建立如图所示空间直角坐标系,,,,.
,,,
则,,
所以,,又,
所以平面,即截面为等腰梯形.
由题可知,,所以等腰梯形的高为,
故截面图形的面积为.故选D.
2.答案:C
解析:根据斜二测画法还原得下图,
因为,所以
所以原图形的面积
故选:C.
3.答案:C
解析:根据斜二测画法的知识可知,
,,
所以图形的面积是.
故选:C.
4.答案:B
解析:如图底面半径为的圆锥中,侧面积为,
所以,由勾股定理得,
所以该圆锥的体积.
故选:B.
5.答案:A
解析:因为平行于轴,所以在中,,
又因为是中边的中点,所以D是BC的中点,
所以.
故选:A
6.答案:A
解析:根据函数的表达式可知,构造三棱锥,其中,,,且,,,
由余弦定理可得,,,,
的最小值即为的最小值,
将三棱锥按照展开可得展开图,且,,
故的最小值为.
故选:A.
7.答案:B
解析:延长AF,且AF与相交于G,连接EG,并与相交于D,连接FD,则四边形AEDF为所求的截面.
在中,由,,得.
在中,由,,得.
因为F为的中点,所以由平面几何知识可知,.
所以,,即G为AG的中点,所以.
又由,可得,
又,,所以.
在中,由,,得,所以.
所以在中,有,,,
即,所以.又注意到,
,
则四边形AEDF的面积为.
故选:B.
8.答案:A
解析:圆台的母线长为,
其侧面展开图的面积.
故选:A.
9.答案:AC
解析:对选项A:母线长,侧面积为,正确;
对选项B:中,,,则当时,
,错误;
对选项C:为等腰直角三角形,,
将放平得到,如图2所示,当,E,C三点共线时最小,F为AB中点,
连接,则,,
,正确;
对选项D:如图3,设截面为SMN,Q为MN中点,
连接OQ,SQ,设,,
则,
当,即时等号成立,D错误.
故选:AC.
10.答案:AD
解析:由题意得到原的平面图为:
其中,,,
,
的AB、AD、AC三条线段中最长的是AB,最短的是AD,故选AD.
11.答案:ABC
解析:
12.答案:ABD
解析:由题意知.对于A,若平面ABC,则.又,平面PAC,,三棱锥的四个面均为直角三角形,A为真命题.对于B,由已知得M为的外心,.平面ABC,则,,,由三角形全等可知,故B为真命题.对于C,要使的面积最小,只需CM最短,在中,,,故C为假命题.对于D,设点P在平面ABC内的射影为O,且O为内切圆的圆心,由平面几何知识得的内切圆的半径,且.在中,,点P到平面ABC的距离为,故D为真命题.
13.答案:
解析:正方体中,平面ABCD,,
又,,则到直线CE的距离为.
故答案为:
14.答案:
解析:连接交于点O,连接OE,平面,平面平面,,是异面直线与CE所成的角.设该正方体的棱长为1,则.又O为的中点,是的中位线,,.在中,由余弦定理的推论得.
15.答案:相交;平行
解析:是的中点,直线DM与直线相交,与平面有一个公共点,与平面相交.取的中点,连接,.,,.,,.四边形为平行四边形,,平面.
16.答案:,
解析:①由题意作出平面图及翻折后的图形.三棱锥的底面三角形BCD面积为定值.当点A离平面BCD的距离最大,即当平面平面BCD时,最大.
又平面平面且()
平面BCD,
.
②.侧棱垂直于底面且底面是由普通三角形的三棱锥外接球球心满足,O是球心,是底面外接圆圆心.
在中,由余弦定理,.
由正弦定理,,在中,外接圆半径R满足,.
17、
(1)答案:见解析
解析:连接,
是正方形,E是的中点,
E是的中点,F是的中点,
,平面,平面,
平面.
(2)答案:
解析:建立如图所示空间直角坐标系,设,
则,,,,
,,,
设平面的法向量,则,
取得,设与平面所成角为,
则.
18、
(1)答案:见解析
解析:因为,平面PDC,平面PDC,
所以平面PDC.又因为平面平面,且平面PAB,所以.
(2)答案:存在点M,使得平面MBD,此时,理由见解析
解析:存在点M,使得PA∥平面MBD,此时.证明如下:连接AC交BD于点O,连接MO.
因为,且,所以,又因为,,
所以,因为平面,平面,所以平面.
19.答案:
解析:如图,设圆锥的底面半径为R,圆柱的底面半径为r.
则,,,.
易知,,即,
,
则圆柱的底面积,
圆柱的侧面积.
.
20.答案:(1)见解析
(2),.原因见解析
解析:(1),,,,.
又,,O为与的公共点.
又,,a,b,c三线共点.
(2)解:,,原因如下:
,,,.
,,,.同理可证.
21.答案:(1)见解析
(2)
解析:(1)在正方形ABCD中,,
又侧面底面ABCD,侧面底面.
平面PAD.平面PAD,.
是正三角形,M是PD的中点,.
又,平面PCD.
(2)解:取AD,BC的中点分别为E,F,连接EF,PE,PF.
则,.
又在正中,.
,平面PEF.
正方形ABCD中,,平面PEF.
是侧面PBC与底面ABCD所成二面角的平面角.
由平面PAD,,平面PAD.平面PAD,
.设正方形ABCD的边长,则,.
,,
即侧面PBC与底面ABCD所成二面角的余弦值为.
22.答案:
解析:由题意,需贴瓷砖的部分为四棱柱与四棱台的侧面积.
,
四棱台的斜高,
,
故需要瓷砖的面积为.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.已知正方体的外接球表面积为,点E为棱的中点,且平面,点平面,则平面截正方体所得的截面图形的面积为( )
A. B. C. D.
2.如图所示,已知正方形的边长为1,它是水平放置的一个平面图形的直观图,则其原图形的面积为( )
A.1 B. C. D.8
3.已知正方形OABC的边长为2,它的水平放置的一个平面图形的直观图为(在轴上),则图形的面积是( )
A.4 B.2 C. D.1
4.在底面半径为1的圆锥中,若该圆锥侧面展开图的面积是,则该圆锥的体积为( )
A. B. C. D.
5.水平放置的的直观图如图所示,是中边的中点,且平行于轴,则,,对应于原中的线段AB,AD,AC,对于这三条线段,正确的判断是( )
A.最短的是AD B.最短的是AC C. D.
6.我们知道立体图形上的最短路径问题通常是把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.请根据此方法求函数的最小值( )
A. B. C. D.
7.已知在直三棱柱中,E,F分别为,的中点,,,,,如图所示,若过A,E,F三点的平面作该直三棱柱的截面,则所得截面的面积为( )
A. B. C. D.
8.已知某圆台的高为,上底面半径为1,下底面半径为2,则其侧面展开图的面积为( )
A.9π B. C. D.
二、多项选择题
9.已知AC为圆锥SO底面圆O的直径(S为顶点,O为圆心),点B为圆O上异于A,C的动点,,则下列结论正确的为( )
A. 圆锥SO的侧面积为
B.的取值范围为
C.若,E为线段AB上的动点,则
D. 过该圆锥顶点S的平面截此圆锥所得截面面积的最大值为
10.如图所示的是水平放置的三角形直观图,是中边上的一点,且,又轴,那么原的AB、AD、AC三条线段中( )
A.最长的是AB B.最长的是AC
C.最短的是AC D.最短的是AD
11.如图,正方体中,O为底面ABCD的中心,M为棱的中点,则下列结论中正确的是( )
A.平面
B.平面MAC
C.异面直线与AC所成的角为60°
D.平面ABCD
12.已知的三边长分别为,,,M是AB边上的点,P是平面ABC外一点.给出下列四个命题,其中是真命题的有( )
A.若平面ABC,则三棱锥的四个面都是直角三角形
B.若平面ABC,且M是AB边的中点,则
C.若,平面ABC,则面积的最小值为
D.若,P在平面ABC内的射影是内切圆的圆心,则点P到平面ABC的距离为
三、填空题
13.在棱长为1的正方体中,E为的中点,则点到直线CE的距离为______.
14.如图,E是正方体的棱上一点,直线平面,则异面直线与CE所成的角的余弦值为__________.
四、双空题
15.如图,在正方体中,M是的中点,则直线DM与平面的位置关系是____________,直线DM与平面的位置关系是_______________.
16.如图,平面四边形中,,,,,将沿着折起,则三棱锥的体积最大值为________,三棱锥体积最大时其外接球的表面积为_________.
五、解答题
17.如图,四棱锥中,为正三角形,为正方形,平面平面,E、F分别为、中点.
(1)证明:平面;
(2)求直线与平面所成角的正弦值.
18.如图所示,已知ABCD为梯形,,,M为线段PC上一点.
(1)设平面平面,证明:.
(2)在棱PC上是否存在点M,使得平面MBD?若存在,请确定点M的位置;若不存在,请说明理由.
19.如图,在底面半径为2,母线长为4的圆锥中内接一个高为的圆柱,求圆柱的表面积.
20.已知是三个平面,且,,.
(1)若,求证:a,b,c三线共点.
(2),则a与c,b与c有什么关系 为什么
21.如图,在四棱锥中,底面ABCD为正方形,侧面PAD是正三角形,侧面底面ABCD,M是PD的中点.
(1)求证:平面PCD;
(2)求侧面PBC与底面ABCD所成二面角的余弦值.
22.如图是一个烟筒的直观图(图中数据的单位为厘米),它的下部是一个正四棱台形物体,上部是一个正四棱柱形物体(底面与四棱台形物体的上底面重合).为防止雨水的侵蚀,同时使烟筒更美观,现要在烟筒外部粘贴瓷砖,请你计算需要多少平方厘米的瓷砖?(结果精确到,可用计算工具)
参考答案
1.答案:D
解析:设该正方体外接球的半径为R,依题意,,解得,故,则,解得.
分别取棱AB,BC的中点F,G,连接,,,,
根据正方体的性质可知:四边形为等腰梯形,建立如图所示空间直角坐标系,,,,.
,,,
则,,
所以,,又,
所以平面,即截面为等腰梯形.
由题可知,,所以等腰梯形的高为,
故截面图形的面积为.故选D.
2.答案:C
解析:根据斜二测画法还原得下图,
因为,所以
所以原图形的面积
故选:C.
3.答案:C
解析:根据斜二测画法的知识可知,
,,
所以图形的面积是.
故选:C.
4.答案:B
解析:如图底面半径为的圆锥中,侧面积为,
所以,由勾股定理得,
所以该圆锥的体积.
故选:B.
5.答案:A
解析:因为平行于轴,所以在中,,
又因为是中边的中点,所以D是BC的中点,
所以.
故选:A
6.答案:A
解析:根据函数的表达式可知,构造三棱锥,其中,,,且,,,
由余弦定理可得,,,,
的最小值即为的最小值,
将三棱锥按照展开可得展开图,且,,
故的最小值为.
故选:A.
7.答案:B
解析:延长AF,且AF与相交于G,连接EG,并与相交于D,连接FD,则四边形AEDF为所求的截面.
在中,由,,得.
在中,由,,得.
因为F为的中点,所以由平面几何知识可知,.
所以,,即G为AG的中点,所以.
又由,可得,
又,,所以.
在中,由,,得,所以.
所以在中,有,,,
即,所以.又注意到,
,
则四边形AEDF的面积为.
故选:B.
8.答案:A
解析:圆台的母线长为,
其侧面展开图的面积.
故选:A.
9.答案:AC
解析:对选项A:母线长,侧面积为,正确;
对选项B:中,,,则当时,
,错误;
对选项C:为等腰直角三角形,,
将放平得到,如图2所示,当,E,C三点共线时最小,F为AB中点,
连接,则,,
,正确;
对选项D:如图3,设截面为SMN,Q为MN中点,
连接OQ,SQ,设,,
则,
当,即时等号成立,D错误.
故选:AC.
10.答案:AD
解析:由题意得到原的平面图为:
其中,,,
,
的AB、AD、AC三条线段中最长的是AB,最短的是AD,故选AD.
11.答案:ABC
解析:
12.答案:ABD
解析:由题意知.对于A,若平面ABC,则.又,平面PAC,,三棱锥的四个面均为直角三角形,A为真命题.对于B,由已知得M为的外心,.平面ABC,则,,,由三角形全等可知,故B为真命题.对于C,要使的面积最小,只需CM最短,在中,,,故C为假命题.对于D,设点P在平面ABC内的射影为O,且O为内切圆的圆心,由平面几何知识得的内切圆的半径,且.在中,,点P到平面ABC的距离为,故D为真命题.
13.答案:
解析:正方体中,平面ABCD,,
又,,则到直线CE的距离为.
故答案为:
14.答案:
解析:连接交于点O,连接OE,平面,平面平面,,是异面直线与CE所成的角.设该正方体的棱长为1,则.又O为的中点,是的中位线,,.在中,由余弦定理的推论得.
15.答案:相交;平行
解析:是的中点,直线DM与直线相交,与平面有一个公共点,与平面相交.取的中点,连接,.,,.,,.四边形为平行四边形,,平面.
16.答案:,
解析:①由题意作出平面图及翻折后的图形.三棱锥的底面三角形BCD面积为定值.当点A离平面BCD的距离最大,即当平面平面BCD时,最大.
又平面平面且()
平面BCD,
.
②.侧棱垂直于底面且底面是由普通三角形的三棱锥外接球球心满足,O是球心,是底面外接圆圆心.
在中,由余弦定理,.
由正弦定理,,在中,外接圆半径R满足,.
17、
(1)答案:见解析
解析:连接,
是正方形,E是的中点,
E是的中点,F是的中点,
,平面,平面,
平面.
(2)答案:
解析:建立如图所示空间直角坐标系,设,
则,,,,
,,,
设平面的法向量,则,
取得,设与平面所成角为,
则.
18、
(1)答案:见解析
解析:因为,平面PDC,平面PDC,
所以平面PDC.又因为平面平面,且平面PAB,所以.
(2)答案:存在点M,使得平面MBD,此时,理由见解析
解析:存在点M,使得PA∥平面MBD,此时.证明如下:连接AC交BD于点O,连接MO.
因为,且,所以,又因为,,
所以,因为平面,平面,所以平面.
19.答案:
解析:如图,设圆锥的底面半径为R,圆柱的底面半径为r.
则,,,.
易知,,即,
,
则圆柱的底面积,
圆柱的侧面积.
.
20.答案:(1)见解析
(2),.原因见解析
解析:(1),,,,.
又,,O为与的公共点.
又,,a,b,c三线共点.
(2)解:,,原因如下:
,,,.
,,,.同理可证.
21.答案:(1)见解析
(2)
解析:(1)在正方形ABCD中,,
又侧面底面ABCD,侧面底面.
平面PAD.平面PAD,.
是正三角形,M是PD的中点,.
又,平面PCD.
(2)解:取AD,BC的中点分别为E,F,连接EF,PE,PF.
则,.
又在正中,.
,平面PEF.
正方形ABCD中,,平面PEF.
是侧面PBC与底面ABCD所成二面角的平面角.
由平面PAD,,平面PAD.平面PAD,
.设正方形ABCD的边长,则,.
,,
即侧面PBC与底面ABCD所成二面角的余弦值为.
22.答案:
解析:由题意,需贴瓷砖的部分为四棱柱与四棱台的侧面积.
,
四棱台的斜高,
,
故需要瓷砖的面积为.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
