1.2.2直角三角形全等的判定课件 18张PPT 2023-2024学年度北师大版数学八年级下册
文档属性
| 名称 | 1.2.2直角三角形全等的判定课件 18张PPT 2023-2024学年度北师大版数学八年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 161.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-27 16:47:09 | ||
图片预览



文档简介
(共18张PPT)
1.2.2 直角三角形全等的判定
1. 探索并理解直角三角形全等的判定方法“HL”.
2. 会用直角三角形全等的判定方法“HL”判定两个直角三角形全等.
学习目标
难点
重点
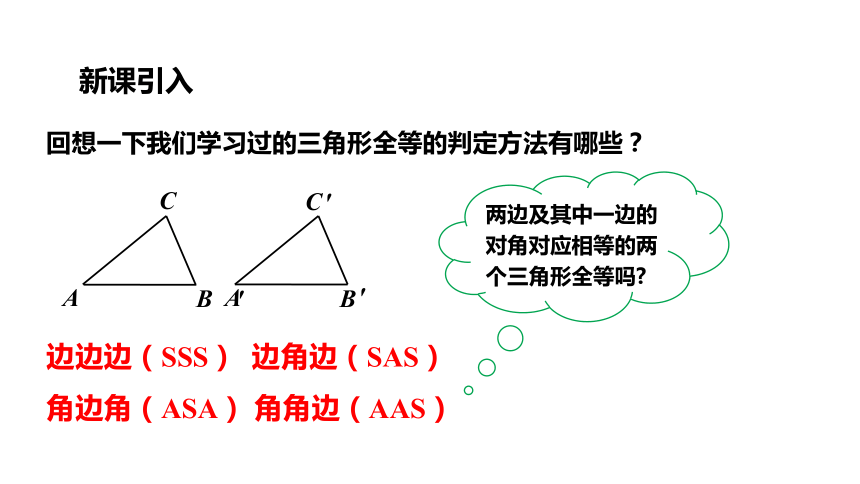
回想一下我们学习过的三角形全等的判定方法有哪些?
两边及其中一边的对角对应相等的两个三角形全等吗
'
C
C
A
B
'
'
B
A
边边边(SSS) 边角边(SAS)
角边角(ASA) 角角边(AAS)
新课引入
C
B
A
F
E
D
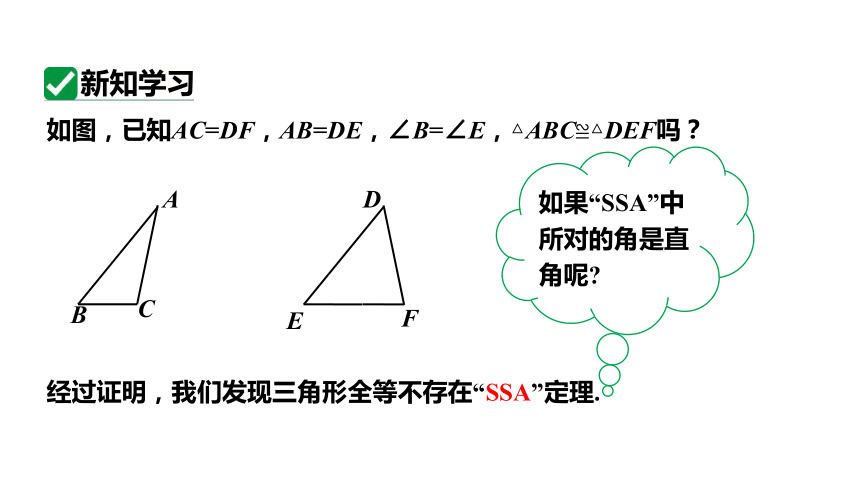
经过证明,我们发现三角形全等不存在“SSA”定理.
如图,已知AC=DF,AB=DE,∠B=∠E,△ABC≌△DEF吗?
如果“SSA”中所对的角是直角呢
新知学习
探究
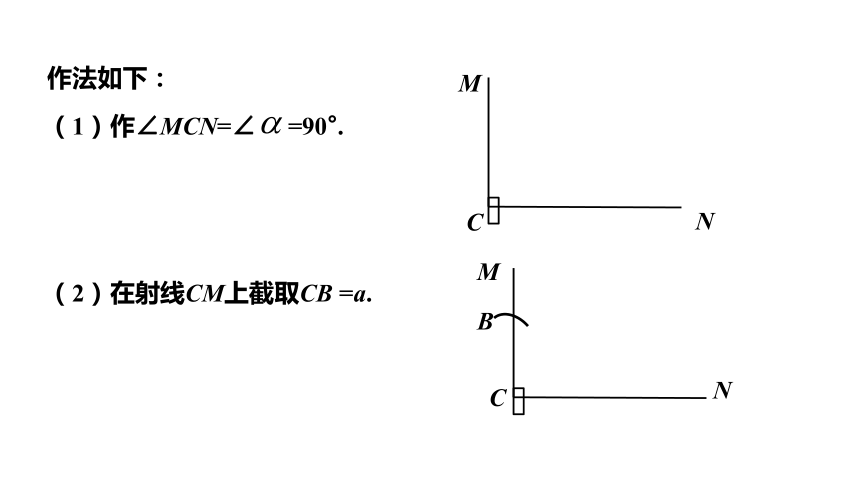
已知一条直角边和斜边,求作一个直角三角形.
如图,已知线段a,c( a < c ),直角α.
求作:Rt△ABC,使∠C=∠α,BC=a,AB=c.
作法如下:
(2)在射线CM上截取CB =a.
(1)作∠MCN=∠ =90°.
M
C
N
M
C
N
B
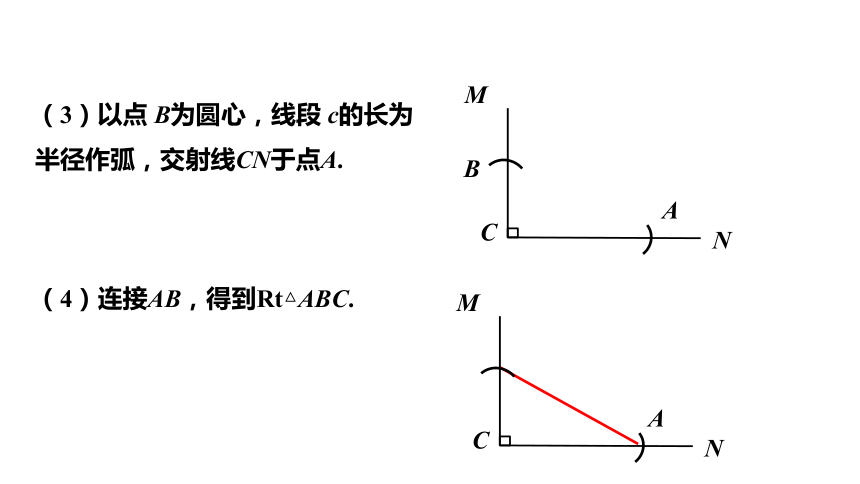
(3)以点 B为圆心,线段 c的长为半径作弧,交射线CN于点A.
(4)连接AB,得到Rt△ABC.
M
C
N
M
C
N
B
A
A
思考
比较小明作的直角三角形和已知三角形,发现它们全等.
猜想:斜边和一条直角边对应相等的两个直角三角形全等;
你能证明吗
证明
已知:如图,在△ABC和△A′B′C′中, ∠C=∠C′=90°,AB=A′B′ ,
AC=A′C ′.
求证:△ABC≌△A′B′C′
A
B
C
A′
B′
C′
证明:在△ABC中,∵∠C=90°
∴BC2=AB2-AC2
同理,B′C′2=A′B′2-A′C′2
∵AB=A′B′,AC=A′C′,
∴BC=B′C′ ∴ △ABC≌ △A′B′C′(SSS)
归纳
直角三角形全等的判定定理:
定理:斜边和一条直角边分别相等的两个直角三角形全等.
简述为:“斜边、直角边”或“HL”
符号语言:
在Rt△ABC和Rt△ A′B′C′ 中,
AB=A′B′
BC=B′C′
∴Rt△ABC ≌Rt△ A′B′C′ (HL).
A
B
C
A′
B′
C′
归纳
直角三角形全等的判定除了可以用“SAS”,“ASA”,“SSS”,“AAS”定理外,“HL”是直角三角形所独有的判定全等的定理.
例 如图,有两个长度相等的滑梯,左边滑梯的高度 AC 与右边滑梯水平方向的长度 DF 相等,两个滑梯的倾斜角∠B 和∠F 的大小有什么关系?
解:根据题意可知∠BAC =∠EDF = 90°,
BC =EF,AC =DF.
∴Rt△BAC≌Rt△EDF(HL).
∴∠B =∠DEF
∵∠DEF +∠F =90° ∴∠B +∠F =90°.
课堂练习
1. 如图所示,P是∠BAC内一点,且点P到AB,AC的距离PF=PE,则能直接得到△PEA≌△PFA的理由是( )
A.HL B.AAS C.SSS D.SAS
A
2.如图,若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充条件( )
A.∠BAC=∠BAD B.AC=AD或BC=BD C.AC=AD且BC=BD D.以上都不正确
B
3.下列可使两个直角三角形全等的条件是( )
A.一条边对应相等 B.两条直角边对应相等
C.一个锐角对应相等 D.两个锐角对应相等
B
4.如图所示,H是△ABC的高AD,BE的交点,且DH=DC,则下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD中正确的有( )
A.1个 B.2个 C.3个 D.4个
B
A
B
C
E
D
H
5.如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.
求证:Rt△ABF≌Rt△DCE.
证明:∵BE=CF,
∴BE+EF=CF+EF,即BF=CE,
∵∠A=∠D=90°,
∴△ABF与△DCE都为直角三角形,
∴Rt△ABF≌Rt△DCE(HL).
BF=CE
AB=CD
在Rt△ABF和Rt△DCE中,
板书设计
“斜边、直角边”
内容
斜边和一条直角边对应相等的两个直角三角形全等
前提条件
在直角三角形中
使用方法
在判定直角三角形全等时,只需找除直角外的两个条件即可(其中至少有一个条件是一组对应边相等)
1.2.2 直角三角形全等的判定
1. 探索并理解直角三角形全等的判定方法“HL”.
2. 会用直角三角形全等的判定方法“HL”判定两个直角三角形全等.
学习目标
难点
重点
回想一下我们学习过的三角形全等的判定方法有哪些?
两边及其中一边的对角对应相等的两个三角形全等吗
'
C
C
A
B
'
'
B
A
边边边(SSS) 边角边(SAS)
角边角(ASA) 角角边(AAS)
新课引入
C
B
A
F
E
D
经过证明,我们发现三角形全等不存在“SSA”定理.
如图,已知AC=DF,AB=DE,∠B=∠E,△ABC≌△DEF吗?
如果“SSA”中所对的角是直角呢
新知学习
探究
已知一条直角边和斜边,求作一个直角三角形.
如图,已知线段a,c( a < c ),直角α.
求作:Rt△ABC,使∠C=∠α,BC=a,AB=c.
作法如下:
(2)在射线CM上截取CB =a.
(1)作∠MCN=∠ =90°.
M
C
N
M
C
N
B
(3)以点 B为圆心,线段 c的长为半径作弧,交射线CN于点A.
(4)连接AB,得到Rt△ABC.
M
C
N
M
C
N
B
A
A
思考
比较小明作的直角三角形和已知三角形,发现它们全等.
猜想:斜边和一条直角边对应相等的两个直角三角形全等;
你能证明吗
证明
已知:如图,在△ABC和△A′B′C′中, ∠C=∠C′=90°,AB=A′B′ ,
AC=A′C ′.
求证:△ABC≌△A′B′C′
A
B
C
A′
B′
C′
证明:在△ABC中,∵∠C=90°
∴BC2=AB2-AC2
同理,B′C′2=A′B′2-A′C′2
∵AB=A′B′,AC=A′C′,
∴BC=B′C′ ∴ △ABC≌ △A′B′C′(SSS)
归纳
直角三角形全等的判定定理:
定理:斜边和一条直角边分别相等的两个直角三角形全等.
简述为:“斜边、直角边”或“HL”
符号语言:
在Rt△ABC和Rt△ A′B′C′ 中,
AB=A′B′
BC=B′C′
∴Rt△ABC ≌Rt△ A′B′C′ (HL).
A
B
C
A′
B′
C′
归纳
直角三角形全等的判定除了可以用“SAS”,“ASA”,“SSS”,“AAS”定理外,“HL”是直角三角形所独有的判定全等的定理.
例 如图,有两个长度相等的滑梯,左边滑梯的高度 AC 与右边滑梯水平方向的长度 DF 相等,两个滑梯的倾斜角∠B 和∠F 的大小有什么关系?
解:根据题意可知∠BAC =∠EDF = 90°,
BC =EF,AC =DF.
∴Rt△BAC≌Rt△EDF(HL).
∴∠B =∠DEF
∵∠DEF +∠F =90° ∴∠B +∠F =90°.
课堂练习
1. 如图所示,P是∠BAC内一点,且点P到AB,AC的距离PF=PE,则能直接得到△PEA≌△PFA的理由是( )
A.HL B.AAS C.SSS D.SAS
A
2.如图,若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充条件( )
A.∠BAC=∠BAD B.AC=AD或BC=BD C.AC=AD且BC=BD D.以上都不正确
B
3.下列可使两个直角三角形全等的条件是( )
A.一条边对应相等 B.两条直角边对应相等
C.一个锐角对应相等 D.两个锐角对应相等
B
4.如图所示,H是△ABC的高AD,BE的交点,且DH=DC,则下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD中正确的有( )
A.1个 B.2个 C.3个 D.4个
B
A
B
C
E
D
H
5.如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.
求证:Rt△ABF≌Rt△DCE.
证明:∵BE=CF,
∴BE+EF=CF+EF,即BF=CE,
∵∠A=∠D=90°,
∴△ABF与△DCE都为直角三角形,
∴Rt△ABF≌Rt△DCE(HL).
BF=CE
AB=CD
在Rt△ABF和Rt△DCE中,
板书设计
“斜边、直角边”
内容
斜边和一条直角边对应相等的两个直角三角形全等
前提条件
在直角三角形中
使用方法
在判定直角三角形全等时,只需找除直角外的两个条件即可(其中至少有一个条件是一组对应边相等)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
