六年级上册数学人教版数学广角——数与形(课件)(共32张PPT)
文档属性
| 名称 | 六年级上册数学人教版数学广角——数与形(课件)(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-26 12:42:02 | ||
图片预览




文档简介
(共32张PPT)
数与形(一)
数形结合
?
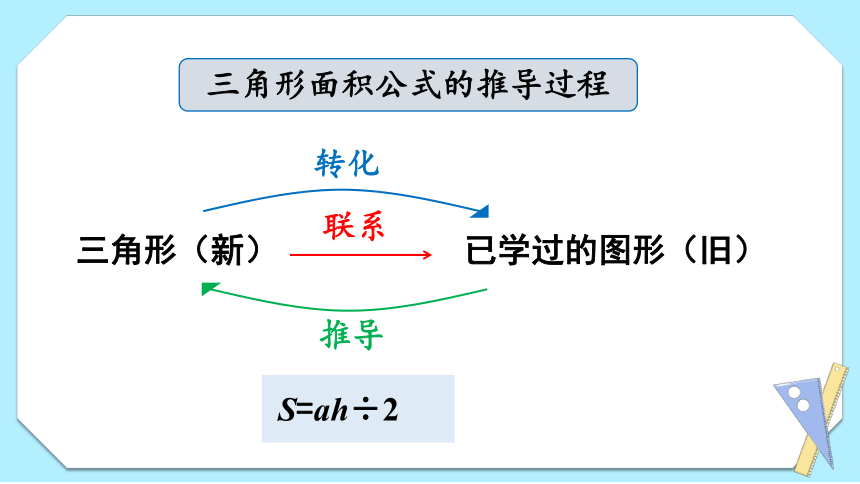
三角形面积公式的推导过程
三角形(新) 已学过的图形(旧)
转化
推导
联系
S=ah÷2
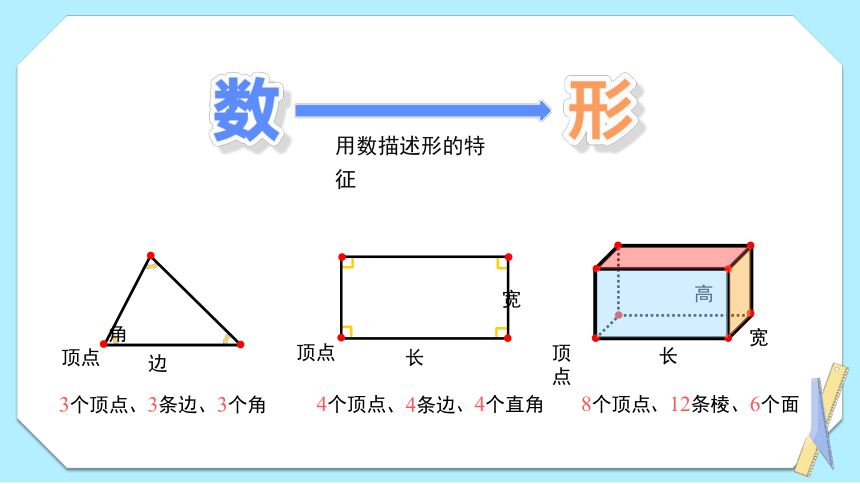
用数描述形的特征
3个顶点
、6个面
长
宽
顶点
边
角
长
宽
高
顶点
顶点
、3条边
、3个角
4个顶点
、4条边
、4个直角
8个顶点
、12条棱
用形表示数的多少
用数描述形的特征
十位
1
个位
1
十位
1
个位
7
十位
2
个位
0
……
3
×
1 8
3
0
4 8
1 6
3
×
6
……
×
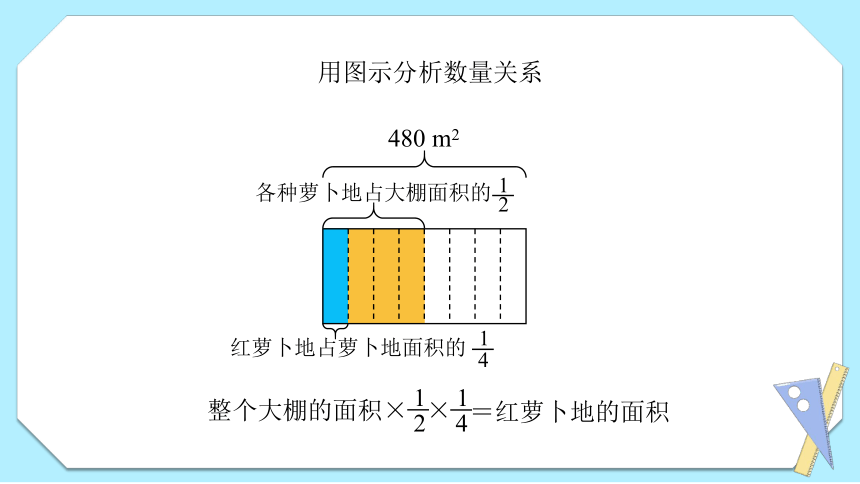
用图示分析数量关系
480 m2
各种萝卜地占大棚面积的
2
1
红萝卜地占萝卜地面积的
4
1
整个大棚的面积× ×
2
1
4
1
=红萝卜地的面积
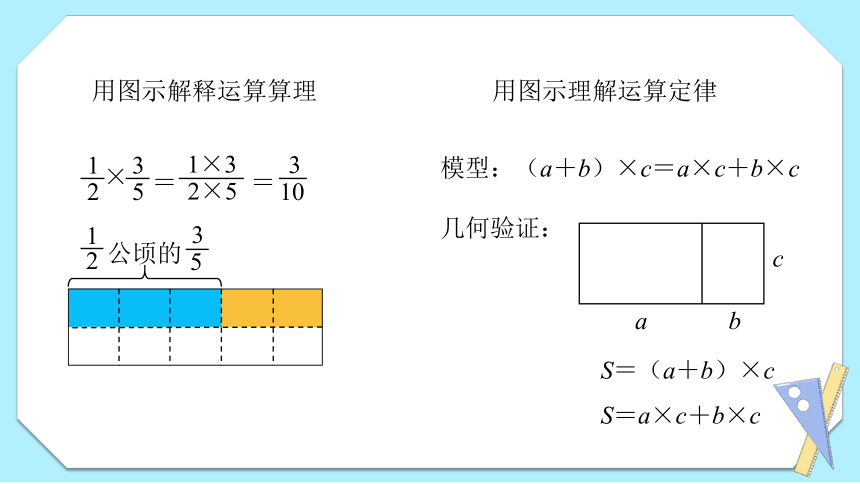
用图示解释运算算理
用图示理解运算定律
模型:(a+b)×c=a×c+b×c
几何验证:
a
b
c
S=(a+b)×c
S=a×c+b×c
公顷的
2
1
5
3
5
3
2
1
×
=
1×3
2×5
=
3
10
观察这组图形,它们之间有什么规律?
1
4
9
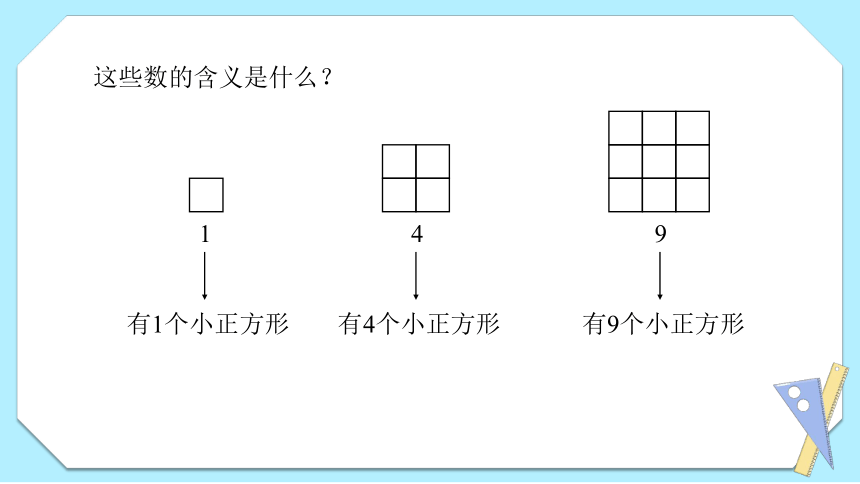
这些数的含义是什么?
有1个小正方形
有4个小正方形
有9个小正方形
1×1
2×2
3×3
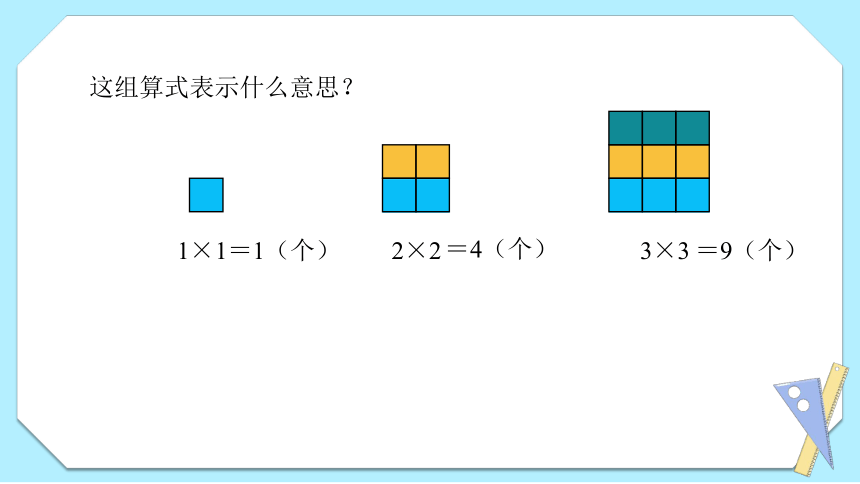
这组算式表示什么意思?
=1(个)
=4(个)
=9(个)
=32(cm2)
=4(cm2)
=22(cm2)
=1(cm2)
=12(cm2)
1×1
2×2
3×3
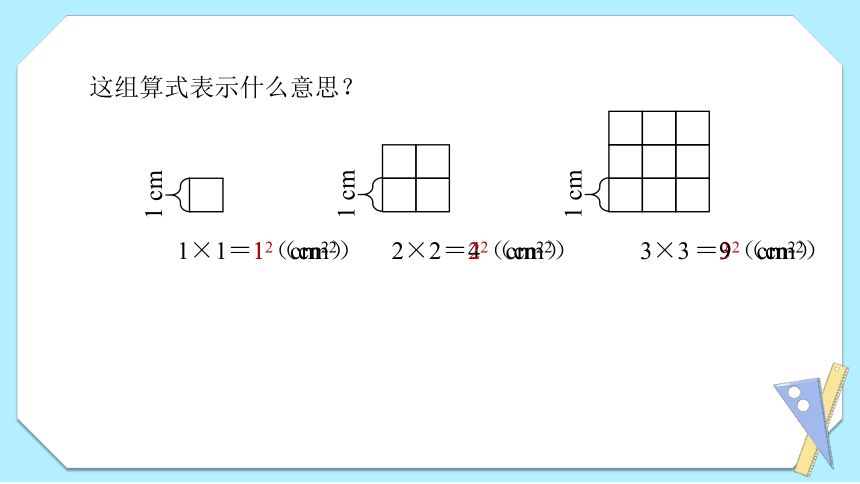
这组算式表示什么意思?
1 cm
1 cm
1 cm
=9(cm2)
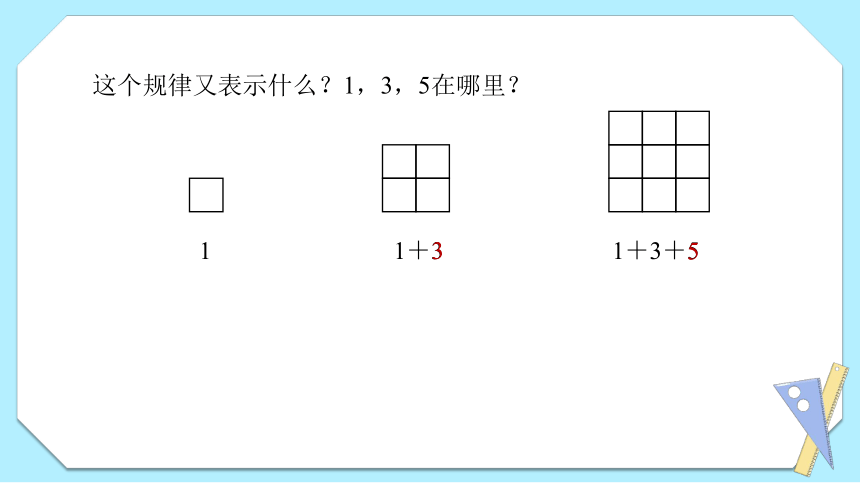
1
1+3
1+3+5
这个规律又表示什么?1,3,5在哪里?
3
5
1
4
9
1×1
2×2
3×3
1
1+3
1+3+5
把这些数或式子用等号连接起来。
=12
=22
=32
=
=
=
=
=
=
1
=1×1
=12
按照这样的规律第四幅图会是什么样子?你能写出算式吗?
=2×2
=4
=22
1+3
=3×3
=9
=32
1+3+5
1
=1×1
=12
=3×3
=9
=32
1+3+5
=2×2
=4
=22
1+3
=4×4
=16
=42
1+3+5+7
观察图形与算式,你发现了什么?
1
=1×1
=12
=3×3
=9
=32
1 +3+5
=2×2
=4
=22
1 +3
=4×4
=16
=42
1 +3+5+7
和是每行或每列小正方形个数的平方
加数与“ ”形小正方形个数对应
加数都是奇数
第几个图形就有几个奇数相加,和就是几的平方
3+5+7=32,对吗?
×
1
3
3
1
5
3
1
5
7
+
+
+
+
+
+
2×2
3×3
4×4
=
=
=
1+3+5+7+9+11+13+15+17+19=
10个连续的奇数相加
= 100
= 9
= 4
= 16
= 32
= 22
= 42
102
从1开始,n个连续奇数的和等于n2。
2.从1开始,几个连续的奇数相加,和就是几的平方。
1.从1开始,几个连续的奇数相加,就可以用
边长是几的大正方形来表示。
1+3+5+7=( )
1+3+5+7+9+11+13 =( )
你能利用规律直接写一写吗?
4
7
1+3+5+7+9+11+13+15+17
=9
2
2
2
1
3
5
7
42
9
11
13
52
62
72
15
82
17
92
易错点:只有从1开始的连续奇数相加的和才是平方数。
3个奇数
1. 请你根据例1的结论算一算。
1+3+5+7+5+3+1 =( )
25
1+3+5+7+9+11+13+11+9+7+5+3+1=( )
85
4个奇数
42
32
+
7个奇数
6个奇数
72
62
+
【教科书P106 做一做 第1题】
照这样接着画下去,第6个图形有多少个绿色小正
方形和多少个蓝色小正方形?第10个图形呢?你能解释这其中的道理吗?
(教材P106 做一做T2)
2.下面每个图中各有多少个绿色小正方形和多少个
蓝色小正方形
绿色:
蓝色:
8
10
12
14
( )
( )
( )
( )
( )
( )
( )
( )
1
2
3
4
第6个图形:6个绿色18个蓝色。
第10个图形:10个绿色26个蓝色。
道理:任意两张相邻的图中,绿色相差1个,蓝色相差2个。
2.下面每个图中各有多少个绿色小正方形和多少个蓝色小正方形
【教科书P106 做一做 第2题】
绿色:
蓝色:
1
8
2
10
3
12
4
14
第6个图形: 绿色:6个 蓝色:2×6+6=18(个)
第10个图形: 绿色:10个 蓝色:2×10+6=26(个)
绿色:
蓝色:
(1)
(8)
(2)
(10)
(3)
(12)
(4)
(14)
解释:从图中可以看出,第n(n>0)个图形一共有
(3n+6)个小正方形,其中有n个绿色小正方
形和(2n+6)个蓝色小正方形。
3. 下面每个图中最外圈有多少个小正方形?
照这样的规律接着画下去,第5个图形最外圈有多少个小正方形?你能解释其中的道理吗?
32-12
52- 32
72- 52
=8
总个数:3行3列
内圈个数:1行1列
【教科书P107 练习二十二 第1题】
照这样的规律接着画下去,第5个图形最外圈有多少个小正方形?你能解释其中的道理吗?
32-12
52- 32
72- 52
=8
总个数:5行5列
内圈个数:3行3列
=16
3. 下面每个图中最外圈有多少个小正方形?
【教科书P107 练习二十二 第1题】
照这样的规律接着画下去,第5个图形最外圈有多少个小正方形?你能解释其中的道理吗?
32-12
52- 32
72- 52
=8
总个数:7行7列
内圈个数:5行5列
=16
=24
3. 下面每个图中最外圈有多少个小正方形?
【教科书P107 练习二十二 第1题】
32-12
=8
52- 32
=16
72- 52
=24
92- 72
=32
112- 92
=40
总个数:11行11列
内圈个数:9行9列
总个数:9行9列
内圈个数:7行7列
照这样的规律接着画下去,第5个图形最外圈有多少个小正方形?你能解释其中的道理吗?
3. 下面每个图中最外圈有多少个小正方形?
【教科书P107 练习二十二 第1题】
1.下面每个图中最外圈各有多少个小正方形?
照这样的规律接着画下去,第5个图形最外圈有多少个小正方形?你能解释这其中的道理吗?
32-1=8
52-32=16
72-52=24
112 -92 =40(个)
解释:因为第n(n>0)个图形最外圈有【(2n+1)2-(2n-1)2】个小正方形,所以第5个图形最外圈有112-92=40(个)小正方形。
(教材P107 练习二十二T1)
4.
请你根据上面图形与数的规律接着画一画,填一填。
15
21
28
【教科书P107 练习二十二 第2题】
1
1+2
1+2+3
1+2+3+4
4.
如果不画,这样排列下去,第10个数是多少
第10个图形中的最后一行是第10行,一共含有55个小圆。
【教科书P107 练习二十二 第2题】
1
1+2
1+2+3
1+2+3+4
第10个数是55。
5.下面每个三角形图各是由多少个小三角形组成的 如果小三角形的边长为1,每个三角形图的周长分别是多少 每个三角形图包含小三角形的个数与这个三角形图的周长之间有什么样的关系
你还能提出什么数学问题
1
3
4
6
9
9
16
12
【教科书P108 练习二十二 第3题】
关系:每个三角形图包含小三角形的个数等于这个三角形图的周长除以3后所得商的平方。
这节课你们都学会了哪些知识?
1.把图形与算式结合起来,是发现规律的关键。
2.从1开始的连续几个奇数的和与正方形数的关系,即有几个连续奇数相加,每边小正方形个数就是几的平方。
从1开始的连续奇数的和正好是这列数个数的平方。
数与形(一)
数形结合
?
三角形面积公式的推导过程
三角形(新) 已学过的图形(旧)
转化
推导
联系
S=ah÷2
用数描述形的特征
3个顶点
、6个面
长
宽
顶点
边
角
长
宽
高
顶点
顶点
、3条边
、3个角
4个顶点
、4条边
、4个直角
8个顶点
、12条棱
用形表示数的多少
用数描述形的特征
十位
1
个位
1
十位
1
个位
7
十位
2
个位
0
……
3
×
1 8
3
0
4 8
1 6
3
×
6
……
×
用图示分析数量关系
480 m2
各种萝卜地占大棚面积的
2
1
红萝卜地占萝卜地面积的
4
1
整个大棚的面积× ×
2
1
4
1
=红萝卜地的面积
用图示解释运算算理
用图示理解运算定律
模型:(a+b)×c=a×c+b×c
几何验证:
a
b
c
S=(a+b)×c
S=a×c+b×c
公顷的
2
1
5
3
5
3
2
1
×
=
1×3
2×5
=
3
10
观察这组图形,它们之间有什么规律?
1
4
9
这些数的含义是什么?
有1个小正方形
有4个小正方形
有9个小正方形
1×1
2×2
3×3
这组算式表示什么意思?
=1(个)
=4(个)
=9(个)
=32(cm2)
=4(cm2)
=22(cm2)
=1(cm2)
=12(cm2)
1×1
2×2
3×3
这组算式表示什么意思?
1 cm
1 cm
1 cm
=9(cm2)
1
1+3
1+3+5
这个规律又表示什么?1,3,5在哪里?
3
5
1
4
9
1×1
2×2
3×3
1
1+3
1+3+5
把这些数或式子用等号连接起来。
=12
=22
=32
=
=
=
=
=
=
1
=1×1
=12
按照这样的规律第四幅图会是什么样子?你能写出算式吗?
=2×2
=4
=22
1+3
=3×3
=9
=32
1+3+5
1
=1×1
=12
=3×3
=9
=32
1+3+5
=2×2
=4
=22
1+3
=4×4
=16
=42
1+3+5+7
观察图形与算式,你发现了什么?
1
=1×1
=12
=3×3
=9
=32
1 +3+5
=2×2
=4
=22
1 +3
=4×4
=16
=42
1 +3+5+7
和是每行或每列小正方形个数的平方
加数与“ ”形小正方形个数对应
加数都是奇数
第几个图形就有几个奇数相加,和就是几的平方
3+5+7=32,对吗?
×
1
3
3
1
5
3
1
5
7
+
+
+
+
+
+
2×2
3×3
4×4
=
=
=
1+3+5+7+9+11+13+15+17+19=
10个连续的奇数相加
= 100
= 9
= 4
= 16
= 32
= 22
= 42
102
从1开始,n个连续奇数的和等于n2。
2.从1开始,几个连续的奇数相加,和就是几的平方。
1.从1开始,几个连续的奇数相加,就可以用
边长是几的大正方形来表示。
1+3+5+7=( )
1+3+5+7+9+11+13 =( )
你能利用规律直接写一写吗?
4
7
1+3+5+7+9+11+13+15+17
=9
2
2
2
1
3
5
7
42
9
11
13
52
62
72
15
82
17
92
易错点:只有从1开始的连续奇数相加的和才是平方数。
3个奇数
1. 请你根据例1的结论算一算。
1+3+5+7+5+3+1 =( )
25
1+3+5+7+9+11+13+11+9+7+5+3+1=( )
85
4个奇数
42
32
+
7个奇数
6个奇数
72
62
+
【教科书P106 做一做 第1题】
照这样接着画下去,第6个图形有多少个绿色小正
方形和多少个蓝色小正方形?第10个图形呢?你能解释这其中的道理吗?
(教材P106 做一做T2)
2.下面每个图中各有多少个绿色小正方形和多少个
蓝色小正方形
绿色:
蓝色:
8
10
12
14
( )
( )
( )
( )
( )
( )
( )
( )
1
2
3
4
第6个图形:6个绿色18个蓝色。
第10个图形:10个绿色26个蓝色。
道理:任意两张相邻的图中,绿色相差1个,蓝色相差2个。
2.下面每个图中各有多少个绿色小正方形和多少个蓝色小正方形
【教科书P106 做一做 第2题】
绿色:
蓝色:
1
8
2
10
3
12
4
14
第6个图形: 绿色:6个 蓝色:2×6+6=18(个)
第10个图形: 绿色:10个 蓝色:2×10+6=26(个)
绿色:
蓝色:
(1)
(8)
(2)
(10)
(3)
(12)
(4)
(14)
解释:从图中可以看出,第n(n>0)个图形一共有
(3n+6)个小正方形,其中有n个绿色小正方
形和(2n+6)个蓝色小正方形。
3. 下面每个图中最外圈有多少个小正方形?
照这样的规律接着画下去,第5个图形最外圈有多少个小正方形?你能解释其中的道理吗?
32-12
52- 32
72- 52
=8
总个数:3行3列
内圈个数:1行1列
【教科书P107 练习二十二 第1题】
照这样的规律接着画下去,第5个图形最外圈有多少个小正方形?你能解释其中的道理吗?
32-12
52- 32
72- 52
=8
总个数:5行5列
内圈个数:3行3列
=16
3. 下面每个图中最外圈有多少个小正方形?
【教科书P107 练习二十二 第1题】
照这样的规律接着画下去,第5个图形最外圈有多少个小正方形?你能解释其中的道理吗?
32-12
52- 32
72- 52
=8
总个数:7行7列
内圈个数:5行5列
=16
=24
3. 下面每个图中最外圈有多少个小正方形?
【教科书P107 练习二十二 第1题】
32-12
=8
52- 32
=16
72- 52
=24
92- 72
=32
112- 92
=40
总个数:11行11列
内圈个数:9行9列
总个数:9行9列
内圈个数:7行7列
照这样的规律接着画下去,第5个图形最外圈有多少个小正方形?你能解释其中的道理吗?
3. 下面每个图中最外圈有多少个小正方形?
【教科书P107 练习二十二 第1题】
1.下面每个图中最外圈各有多少个小正方形?
照这样的规律接着画下去,第5个图形最外圈有多少个小正方形?你能解释这其中的道理吗?
32-1=8
52-32=16
72-52=24
112 -92 =40(个)
解释:因为第n(n>0)个图形最外圈有【(2n+1)2-(2n-1)2】个小正方形,所以第5个图形最外圈有112-92=40(个)小正方形。
(教材P107 练习二十二T1)
4.
请你根据上面图形与数的规律接着画一画,填一填。
15
21
28
【教科书P107 练习二十二 第2题】
1
1+2
1+2+3
1+2+3+4
4.
如果不画,这样排列下去,第10个数是多少
第10个图形中的最后一行是第10行,一共含有55个小圆。
【教科书P107 练习二十二 第2题】
1
1+2
1+2+3
1+2+3+4
第10个数是55。
5.下面每个三角形图各是由多少个小三角形组成的 如果小三角形的边长为1,每个三角形图的周长分别是多少 每个三角形图包含小三角形的个数与这个三角形图的周长之间有什么样的关系
你还能提出什么数学问题
1
3
4
6
9
9
16
12
【教科书P108 练习二十二 第3题】
关系:每个三角形图包含小三角形的个数等于这个三角形图的周长除以3后所得商的平方。
这节课你们都学会了哪些知识?
1.把图形与算式结合起来,是发现规律的关键。
2.从1开始的连续几个奇数的和与正方形数的关系,即有几个连续奇数相加,每边小正方形个数就是几的平方。
从1开始的连续奇数的和正好是这列数个数的平方。
