解直角三角形3
图片预览




文档简介
课件20张PPT。28.2 解直角三角形(3) 一个人就好象一个分数,他的实际才干就好比分子,而他对自己的估计就好比分母,分母越大,则分数的值就越小.
——托尔斯泰1、我校准备在田径场旁建①②两幢学生公寓,已知每幢公寓的高为15米,太阳光线AC的入射角∠ACD=550,为使②公寓的第一层能照到阳光,现请你设计一下,两幢公寓间距BC至少是( ) 米。
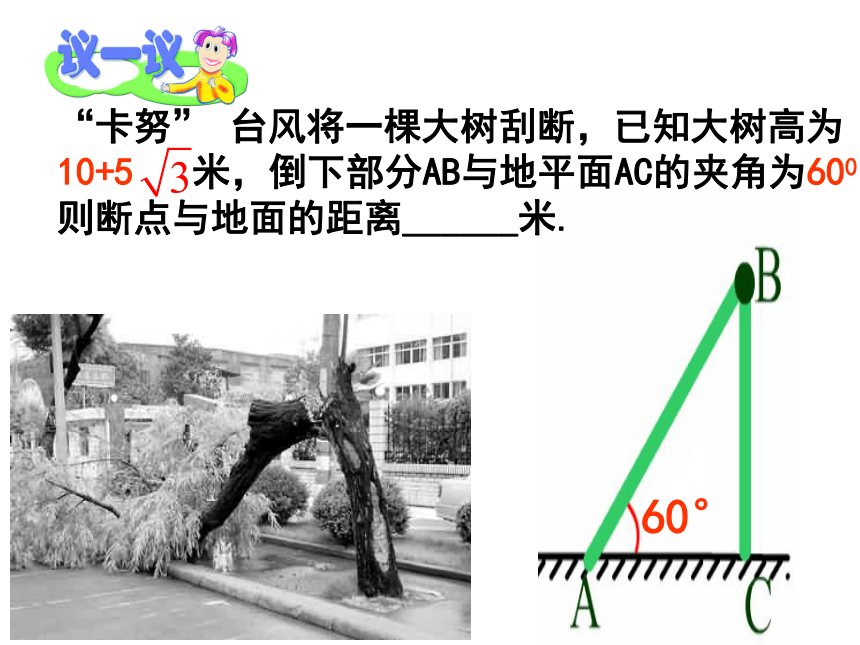
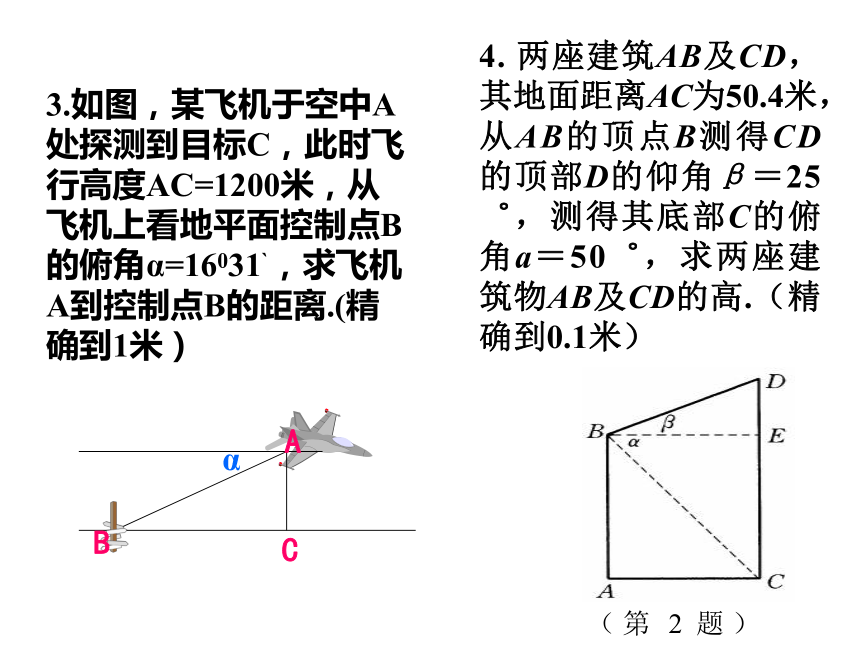
A、15sin550 B、15cos550 C、15tan550 D、15cot550C “卡努” 台风将一棵大树刮断,经测量,大树刮断一端的着地点A到树根部C的距离为4米,倒下部分AB与地平面AC的夹角为450,则这棵大树高是___ __米.45°4米 如果在大树的断点B上方2米处(D),用一根支柱进行加固,地面上的加固点为A,则支柱AD长至少为 米。60°3.如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角α=16031`,求飞机A到控制点B的距离.(精确到1米)αABC4. 两座建筑AB及CD,其地面距离AC为50.4米,从AB的顶点B测得CD的顶部D的仰角β=25゜,测得其底部C的俯角a=50゜,求两座建筑物AB及CD的高.(精确到0.1米)指南或北的方向线与目标方向线构成小于900的角,叫做方向角.
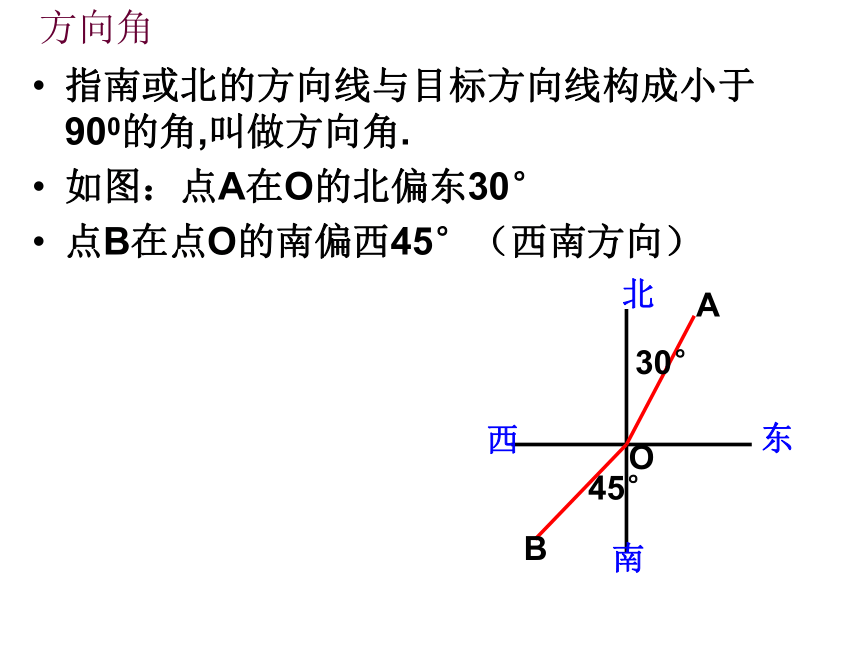
如图:点A在O的北偏东30°
点B在点O的南偏西45°(西南方向)
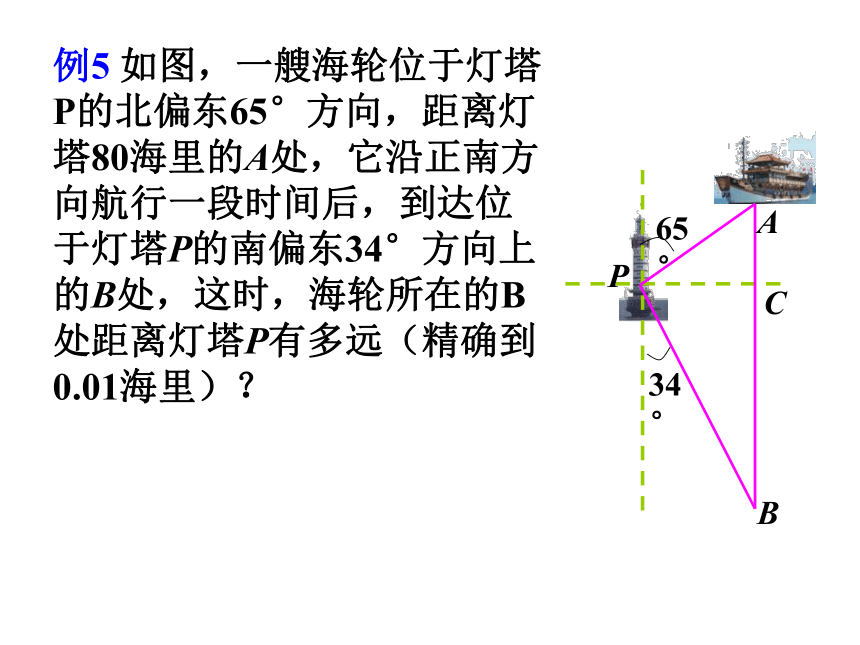
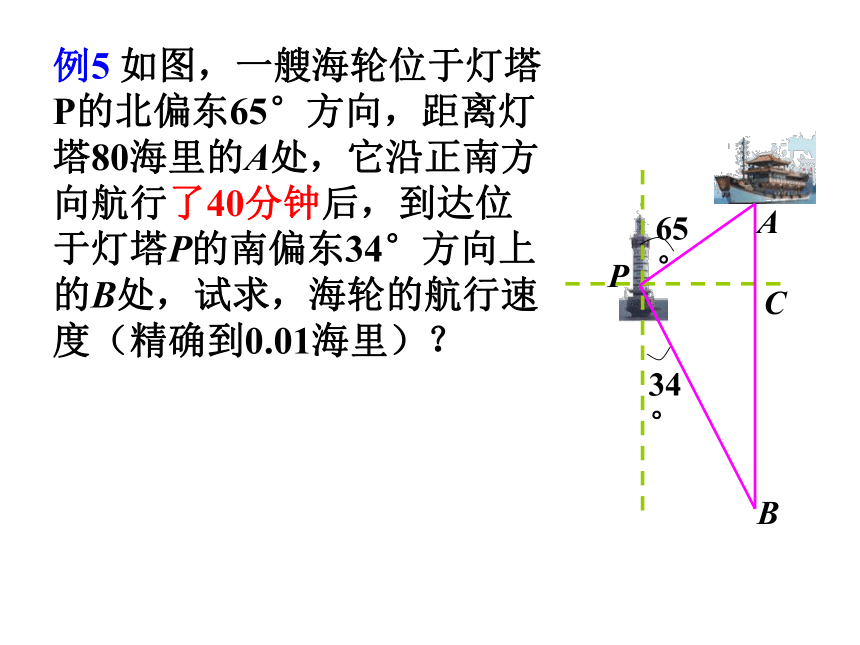
方向角例5 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(精确到0.01海里)?65°34°PBCA65°34°PBCA例5 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行了40分钟后,到达位于灯塔P的南偏东34°方向上的B处,试求,海轮的航行速度(精确到0.01海里)?D练习二: 2、海中有一个小岛A,它的周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏到30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?BADF60°30°30°12 3、前年“云娜”台风中心从我市(看成一个点A)的正东方向300km的B岛以每时25km的速度正面袭击我市,距台风中心250km的范围内均受台风的影响.我市遭到了严重的影响,那么影响时间有多长? 去年“卡努” 台风中心从我市的正东方向300km处向北偏西60度方向移动,其他数据不变,请问此时,我市会受到台风影响吗?若受影响,则影响的时间又多长?4、如图,某轮船沿正北方向航行,在A点处测得灯塔B在北偏西300,船以每小时25海里的速度航行2小时到达C点后,测得灯塔B在北偏西750,问当此船到达灯塔B的正东方向时,船距灯塔B有多远?(结果保留两个有效数字)5. 外国船只,除特许外,不得进入我国海洋100海里以内的区域,如图,设A、B是我们的观察站,A和B 之间的距离为157.73海里,海岸线是过A、B的一条直线,一外国船只在P点,在A点测得∠BAP=450,同时在B点测得∠ABP=600,问此时是否要向外国船只发出警告,令其退出我国海域.D5、 一艘船向东航行,上午8时到达B处,看到有一灯塔在它的北偏东59°,距离为72海里的A处,上午10时到达C处,看到灯塔在它的正北方向.求这艘船航行的速度.(精确到1海里/时)答案:这艘船航行的速度约31 海里/时CBA东北南www.czsx.com.cn6、如图,MN表示某引水工程的一段设计路线,从M到N的走向为南偏东30°,在M的南偏东60°方向上有一点A,以A为圆心、500m为半径的圆形区域为居民区。取MN上的另一点B,测得BA的方向为南偏东75°。已知MB=400m,通过计算回答,如果不改变方向,输水管道是否会穿过居民区。 7、由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。
1)A城是否受到这次沙尘暴的影响,为什么?
(2)若A城受这次沙尘暴的影响,
那么遭受影响的时间有多长?
www.czsx.com.cn 实践活动:明天数学活动课,年级段将组织各班同学去校外测量一铁塔的高度,为了安全起见,不能爬上铁塔测量,只能在地面上进行,那么你需要准备哪些测量工具?(如卷尺、测角仪)小结:1.在解直角三角形及应用时经常接触到的一些概念
2.实际问题向数学模型的转化
3.解直角三角形的边角关系
成功就是99%的汗水,加上1%的灵感。
------爱迪生www.czsx.com.cn如图,我校九(4)班的一个学习小组进行测量孤山高度的实践活动。部分同学在山脚点A测得山腰上一点D的仰角为30°,并测得AD的长度为180米;另一部分同学在山顶点B测得山脚点A的俯角为45°,山腰点D的俯角为60°。请你帮助他们计算出小山的高度BC(计算过程和结果都不取近似值)。
——托尔斯泰1、我校准备在田径场旁建①②两幢学生公寓,已知每幢公寓的高为15米,太阳光线AC的入射角∠ACD=550,为使②公寓的第一层能照到阳光,现请你设计一下,两幢公寓间距BC至少是( ) 米。
A、15sin550 B、15cos550 C、15tan550 D、15cot550C “卡努” 台风将一棵大树刮断,经测量,大树刮断一端的着地点A到树根部C的距离为4米,倒下部分AB与地平面AC的夹角为450,则这棵大树高是___ __米.45°4米 如果在大树的断点B上方2米处(D),用一根支柱进行加固,地面上的加固点为A,则支柱AD长至少为 米。60°3.如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角α=16031`,求飞机A到控制点B的距离.(精确到1米)αABC4. 两座建筑AB及CD,其地面距离AC为50.4米,从AB的顶点B测得CD的顶部D的仰角β=25゜,测得其底部C的俯角a=50゜,求两座建筑物AB及CD的高.(精确到0.1米)指南或北的方向线与目标方向线构成小于900的角,叫做方向角.
如图:点A在O的北偏东30°
点B在点O的南偏西45°(西南方向)
方向角例5 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(精确到0.01海里)?65°34°PBCA65°34°PBCA例5 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行了40分钟后,到达位于灯塔P的南偏东34°方向上的B处,试求,海轮的航行速度(精确到0.01海里)?D练习二: 2、海中有一个小岛A,它的周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏到30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?BADF60°30°30°12 3、前年“云娜”台风中心从我市(看成一个点A)的正东方向300km的B岛以每时25km的速度正面袭击我市,距台风中心250km的范围内均受台风的影响.我市遭到了严重的影响,那么影响时间有多长? 去年“卡努” 台风中心从我市的正东方向300km处向北偏西60度方向移动,其他数据不变,请问此时,我市会受到台风影响吗?若受影响,则影响的时间又多长?4、如图,某轮船沿正北方向航行,在A点处测得灯塔B在北偏西300,船以每小时25海里的速度航行2小时到达C点后,测得灯塔B在北偏西750,问当此船到达灯塔B的正东方向时,船距灯塔B有多远?(结果保留两个有效数字)5. 外国船只,除特许外,不得进入我国海洋100海里以内的区域,如图,设A、B是我们的观察站,A和B 之间的距离为157.73海里,海岸线是过A、B的一条直线,一外国船只在P点,在A点测得∠BAP=450,同时在B点测得∠ABP=600,问此时是否要向外国船只发出警告,令其退出我国海域.D5、 一艘船向东航行,上午8时到达B处,看到有一灯塔在它的北偏东59°,距离为72海里的A处,上午10时到达C处,看到灯塔在它的正北方向.求这艘船航行的速度.(精确到1海里/时)答案:这艘船航行的速度约31 海里/时CBA东北南www.czsx.com.cn6、如图,MN表示某引水工程的一段设计路线,从M到N的走向为南偏东30°,在M的南偏东60°方向上有一点A,以A为圆心、500m为半径的圆形区域为居民区。取MN上的另一点B,测得BA的方向为南偏东75°。已知MB=400m,通过计算回答,如果不改变方向,输水管道是否会穿过居民区。 7、由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。
1)A城是否受到这次沙尘暴的影响,为什么?
(2)若A城受这次沙尘暴的影响,
那么遭受影响的时间有多长?
www.czsx.com.cn 实践活动:明天数学活动课,年级段将组织各班同学去校外测量一铁塔的高度,为了安全起见,不能爬上铁塔测量,只能在地面上进行,那么你需要准备哪些测量工具?(如卷尺、测角仪)小结:1.在解直角三角形及应用时经常接触到的一些概念
2.实际问题向数学模型的转化
3.解直角三角形的边角关系
成功就是99%的汗水,加上1%的灵感。
------爱迪生www.czsx.com.cn如图,我校九(4)班的一个学习小组进行测量孤山高度的实践活动。部分同学在山脚点A测得山腰上一点D的仰角为30°,并测得AD的长度为180米;另一部分同学在山顶点B测得山脚点A的俯角为45°,山腰点D的俯角为60°。请你帮助他们计算出小山的高度BC(计算过程和结果都不取近似值)。
