华师大版数学九年级下册 27.1.3 圆周角 课件(共15张PPT)
文档属性
| 名称 | 华师大版数学九年级下册 27.1.3 圆周角 课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-28 10:36:11 | ||
图片预览




文档简介
(共15张PPT)
华师大版数学
九年级下册
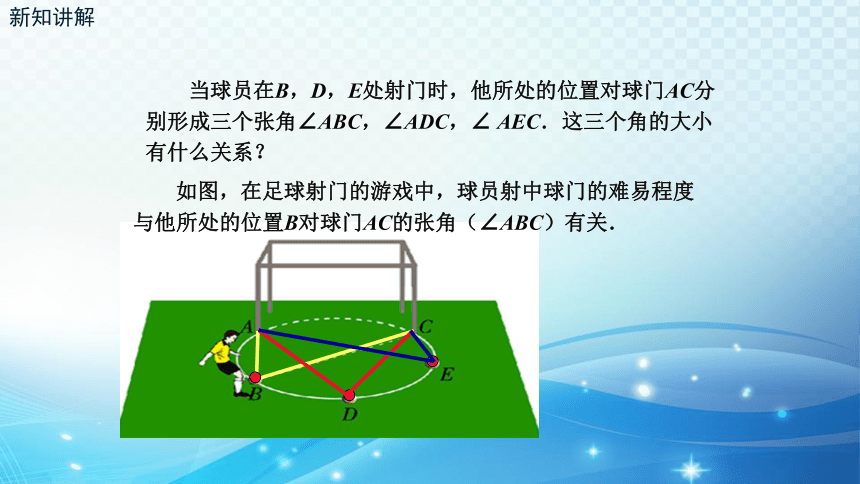
当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,∠ADC,∠ AEC.这三个角的大小有什么关系?
如图,在足球射门的游戏中,球员射中球门的难易程度与他所处的位置B对球门AC的张角(∠ABC)有关.
新知讲解
它们与圆心角有什么区别?
圆周角的定义
思考: ∠ABC,∠ADC,∠ AEC是圆心角吗?
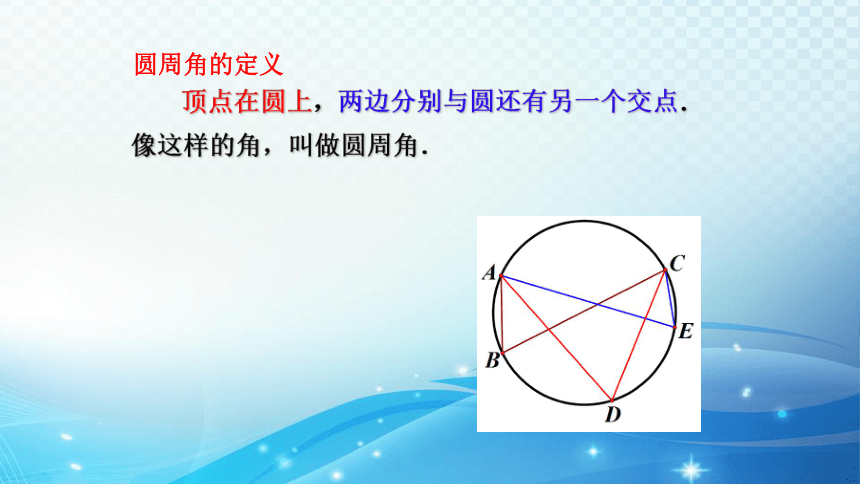
顶点在圆上,两边分别与圆还有另一个交点.
像这样的角,叫做圆周角.
圆周角的定义
∠D = ∠E = ∠F = 40°
如图,∠AOB=80°.
(1)请画出几个 所对的圆周角,这几个圆周角有什么关系?
(2)这些圆周角与圆心角∠AOB的大小有什么关系?
D
E
F
∠D = ∠E = ∠F
圆周角和圆心角的关系
AB
D
E
F
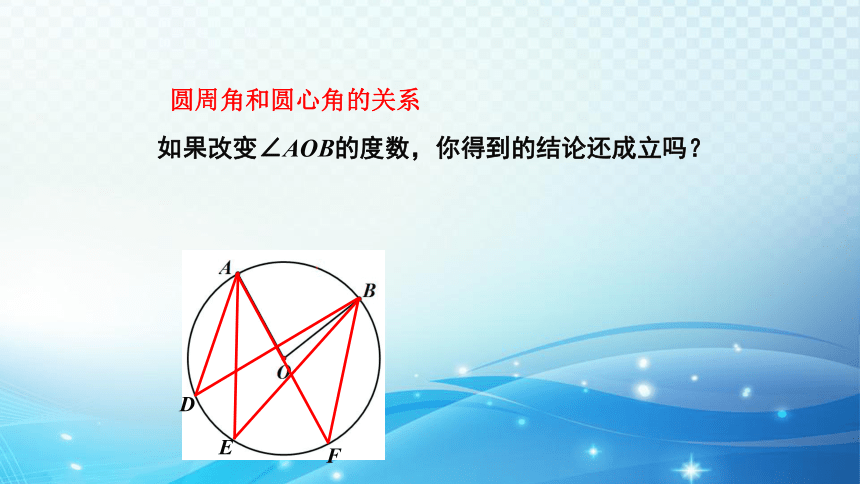
如果改变∠AOB的度数,你得到的结论还成立吗?
圆周角和圆心角的关系
D
E
F
猜想:圆周角的度数等于它所对弧上的圆心角度数的一半.
∠D = ∠E = ∠F
∠D = ∠E = ∠F
圆周角和圆心角的关系
圆周角定理
学以致用
当球员在B,D,E三点射门时,他所处的位置对球门AC形成的三个张角∠ABC,∠ADC,∠ AEC的大小有什么关系?为什么?
O
推论:同弧或等弧所对的圆周角相等.
圆周角定理的推论
根据圆周角和圆心的位置关系,分三种情况讨论:
(1)圆心O在圆周角∠C的一边上,如图(1);
(2)圆心O在圆周角∠C的内部,如图(2);
(3)圆心O在圆周角∠C的外部,如图(3).
数学思想方法---分类讨论
D
D
一般
特殊
数学思想方法---化归思想
转化
1.如图,在直径为AB的半圆中,O为圆心,C,D为半
圆上的两点,∠CAD=25 °,则∠COD = .
2.如图,点B,C在⊙O上,且BO =BC,则圆周
角∠BAC = .
50°
30 °
第1题图
第2题图
巩固练习
3 . AB,AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=35°,求∠BOC的度数.
课堂总结
通过本节课你学到了什么?
华师大版数学
九年级下册
当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,∠ADC,∠ AEC.这三个角的大小有什么关系?
如图,在足球射门的游戏中,球员射中球门的难易程度与他所处的位置B对球门AC的张角(∠ABC)有关.
新知讲解
它们与圆心角有什么区别?
圆周角的定义
思考: ∠ABC,∠ADC,∠ AEC是圆心角吗?
顶点在圆上,两边分别与圆还有另一个交点.
像这样的角,叫做圆周角.
圆周角的定义
∠D = ∠E = ∠F = 40°
如图,∠AOB=80°.
(1)请画出几个 所对的圆周角,这几个圆周角有什么关系?
(2)这些圆周角与圆心角∠AOB的大小有什么关系?
D
E
F
∠D = ∠E = ∠F
圆周角和圆心角的关系
AB
D
E
F
如果改变∠AOB的度数,你得到的结论还成立吗?
圆周角和圆心角的关系
D
E
F
猜想:圆周角的度数等于它所对弧上的圆心角度数的一半.
∠D = ∠E = ∠F
∠D = ∠E = ∠F
圆周角和圆心角的关系
圆周角定理
学以致用
当球员在B,D,E三点射门时,他所处的位置对球门AC形成的三个张角∠ABC,∠ADC,∠ AEC的大小有什么关系?为什么?
O
推论:同弧或等弧所对的圆周角相等.
圆周角定理的推论
根据圆周角和圆心的位置关系,分三种情况讨论:
(1)圆心O在圆周角∠C的一边上,如图(1);
(2)圆心O在圆周角∠C的内部,如图(2);
(3)圆心O在圆周角∠C的外部,如图(3).
数学思想方法---分类讨论
D
D
一般
特殊
数学思想方法---化归思想
转化
1.如图,在直径为AB的半圆中,O为圆心,C,D为半
圆上的两点,∠CAD=25 °,则∠COD = .
2.如图,点B,C在⊙O上,且BO =BC,则圆周
角∠BAC = .
50°
30 °
第1题图
第2题图
巩固练习
3 . AB,AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=35°,求∠BOC的度数.
课堂总结
通过本节课你学到了什么?
