新课标A版选修1-1第三章导数及其应用3.3.2函数的极值与导数
文档属性
| 名称 | 新课标A版选修1-1第三章导数及其应用3.3.2函数的极值与导数 |  | |
| 格式 | rar | ||
| 文件大小 | 112.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-02-20 21:29:00 | ||
图片预览


文档简介
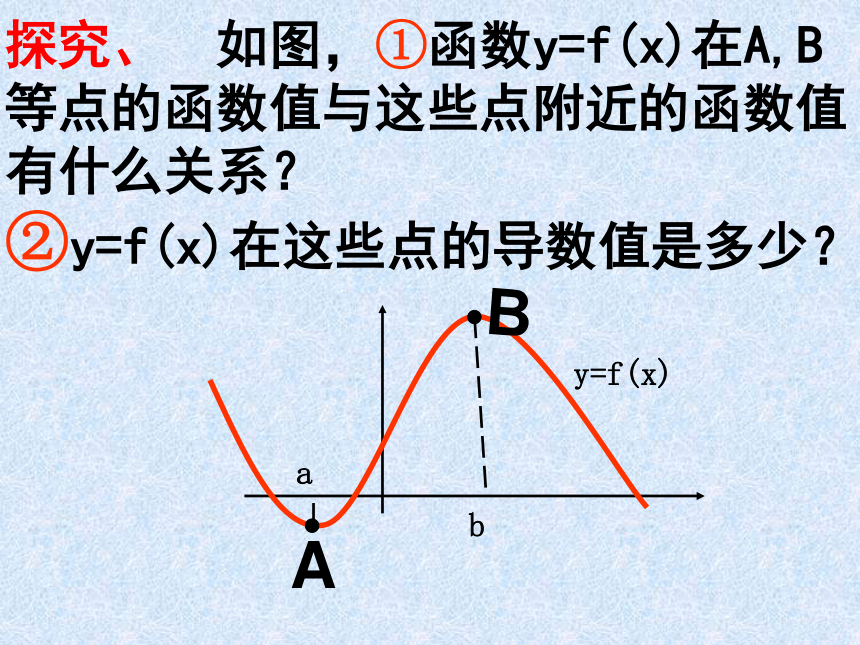
课件16张PPT。注、单调区间不能以“并集”出现。 利用导数讨论函数单调的步骤:(1)求导数(3)下结论 3.3.2 函数的极值与导数探究、 如图,①函数y=f(x)在A,B
等点的函数值与这些点附近的函数值
有什么关系?
②y=f(x)在这些点的导数值是多少?AB探究、 如图,①函数y=g(x)在横坐标
为c,d,e,f,g,h等点的函数值与这些点
附近的函数值有什么关系?
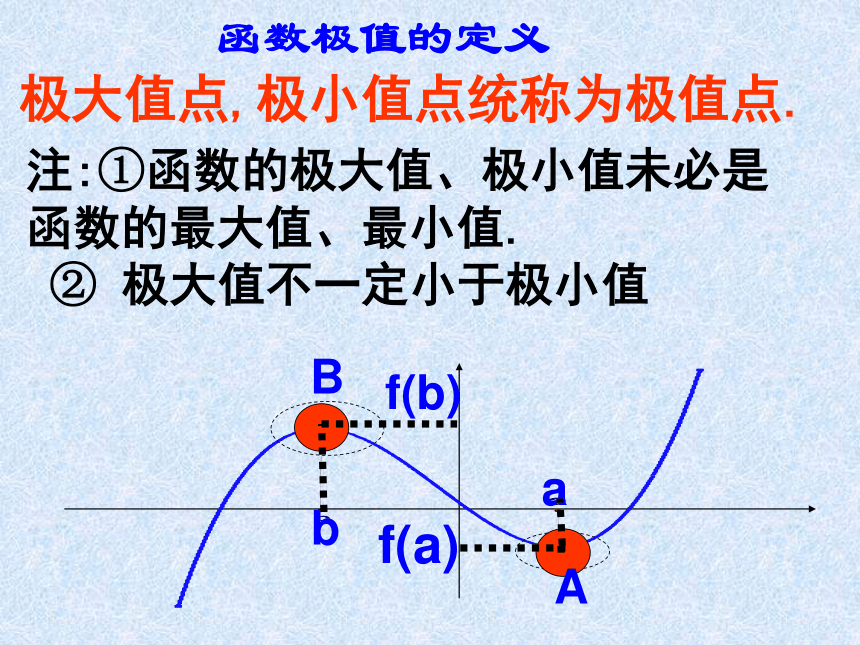
②y=g(x)在这些点的导数值是多少?函数极值的定义极大值点,极小值点统称为极值点.注:①函数的极大值、极小值未必是函数的最大值、最小值.
② 极大值不一定小于极小值f(a)f(b)baBA 一般地,设函数f(x)在点x0附近有定义,如果对x0附近的所有的点,都有f (x0)>f(x),我们就说f (x0)是函数f(x)的一个极大值,记作
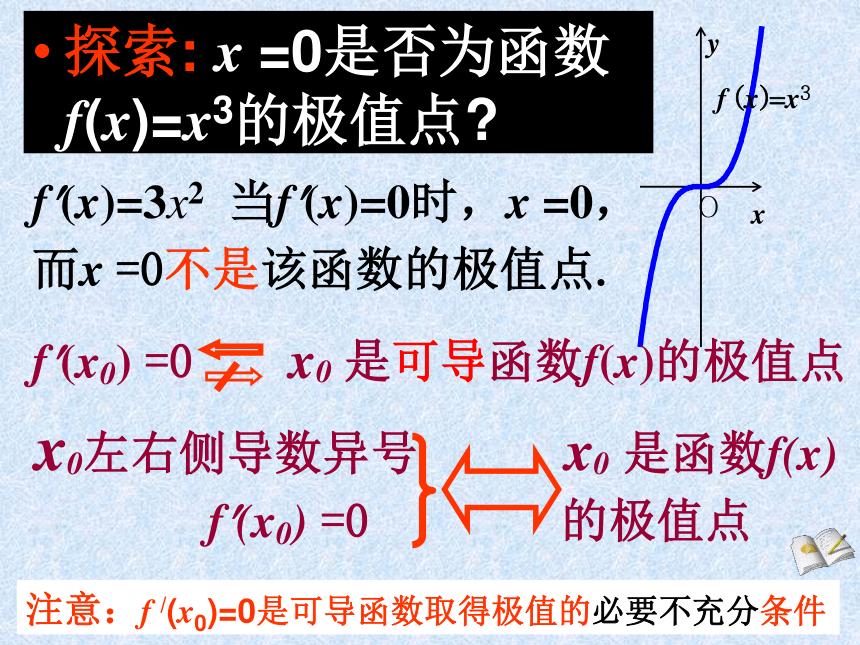
y极大值= f (x0);如果对x0附近的所有的点,都有f (x0) 极大值与极小值同称为极值.函数极值的定义 观察图像并类比函数的单调性与导数关系的研究方法,看极值与导数之间有什么关系?o a x0 b x yo a x0 b x yf?(x) >0f?(x) =0f?(x) <0极大值f?(x) <0f?(x) =0极小值f?(x) >0请问如何判断f (x0)是极大值或是极小值?左正右负为极大,右正左负为极小探索: x =0是否为函数f(x)=x3的极值点?而x =0不是该函数的极值点.f?(x0) =0 x0 是可导函数f(x)的极值点 x0左右侧导数异号 x0 是函数f(x)
的极值点注意:f /(x0)=0是可导函数取得极值的必要不充分条件f?(x)=3x2 当f?(x)=0时,x =0, f?(x0) =0请思考求可导函数的极值的步骤: 强调:要想知道 x0是极大值点还是极小值点就必须判断 f?(x0)=0左右侧导数的符号.注:导数等于零的点不一定是极值点.求下列函数的极值 案例分析函数
在 时有极值10,则a,b的值为( )
A、 或
B、 或
C、C 案例分析函数
在 时有极值10,则a,b的值为( )通过验证,a=3,b=-3不合要求注意代入检验 可导函数y=f(x)的导数y/与函数值和极值之间的关系为( )
A、导数y/由负变正,则函数y由减变为增,且有极大值
B、导数y/由负变正,则函数y由增变为减,且有极大值
C、导数y/由正变负,则函数y由增变为减,且有极小值
D、导数y/由正变负,则函数y由增变为减,且有极大值D练习本节课主要学习了哪些内容?1、极值的判定方法 2、极值的求法注
意
点:2、f /(x0)=0是可导函数取得极值的必要不充分条件3、数形结合以及函数与方程思想的应用1、要想知道 x0是极大值点还是极小值点就必须判断 f?(x0)=0左右侧导数的正负..略解:(1)由图像可知:(2)注意:数形结合以及函数与方程思想的应用
等点的函数值与这些点附近的函数值
有什么关系?
②y=f(x)在这些点的导数值是多少?AB探究、 如图,①函数y=g(x)在横坐标
为c,d,e,f,g,h等点的函数值与这些点
附近的函数值有什么关系?
②y=g(x)在这些点的导数值是多少?函数极值的定义极大值点,极小值点统称为极值点.注:①函数的极大值、极小值未必是函数的最大值、最小值.
② 极大值不一定小于极小值f(a)f(b)baBA 一般地,设函数f(x)在点x0附近有定义,如果对x0附近的所有的点,都有f (x0)>f(x),我们就说f (x0)是函数f(x)的一个极大值,记作
y极大值= f (x0);如果对x0附近的所有的点,都有f (x0)
的极值点注意:f /(x0)=0是可导函数取得极值的必要不充分条件f?(x)=3x2 当f?(x)=0时,x =0, f?(x0) =0请思考求可导函数的极值的步骤: 强调:要想知道 x0是极大值点还是极小值点就必须判断 f?(x0)=0左右侧导数的符号.注:导数等于零的点不一定是极值点.求下列函数的极值 案例分析函数
在 时有极值10,则a,b的值为( )
A、 或
B、 或
C、C 案例分析函数
在 时有极值10,则a,b的值为( )通过验证,a=3,b=-3不合要求注意代入检验 可导函数y=f(x)的导数y/与函数值和极值之间的关系为( )
A、导数y/由负变正,则函数y由减变为增,且有极大值
B、导数y/由负变正,则函数y由增变为减,且有极大值
C、导数y/由正变负,则函数y由增变为减,且有极小值
D、导数y/由正变负,则函数y由增变为减,且有极大值D练习本节课主要学习了哪些内容?1、极值的判定方法 2、极值的求法注
意
点:2、f /(x0)=0是可导函数取得极值的必要不充分条件3、数形结合以及函数与方程思想的应用1、要想知道 x0是极大值点还是极小值点就必须判断 f?(x0)=0左右侧导数的正负..略解:(1)由图像可知:(2)注意:数形结合以及函数与方程思想的应用
