江西省赣州市2023-2024学年高二上学期期末考试数学试题(含答案)
文档属性
| 名称 | 江西省赣州市2023-2024学年高二上学期期末考试数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 655.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-26 17:13:12 | ||
图片预览




文档简介
赣州市2023~2024学年度第一学期期末考试
高二数学试卷
2024年1月
第Ⅰ卷(选择题共60分)
一、单选题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.直线的倾斜角为
A.30° B.60° C.120° D.150°
2.“”是“方程表示的曲线是椭圆”的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
3.已知直线:和:.若,则m的值为
A. B.3 C.1或3 D.或3
4.阅读课上,5名同学分别从3种不同的书中选择一种进行阅读,不同的选法种数是
A.50 B.60 C.125 D.243
5.设F为抛物线C:的焦点,A为平面内定点,若抛物线C上存在点P使得的最小值为5,则点A可以为
A. B. C. D.
6.已知,为双曲线C:(,)的两个焦点,以为直径的圆与C在第一象限的交点为P.若,则C的离心率为
A. B. C. D.
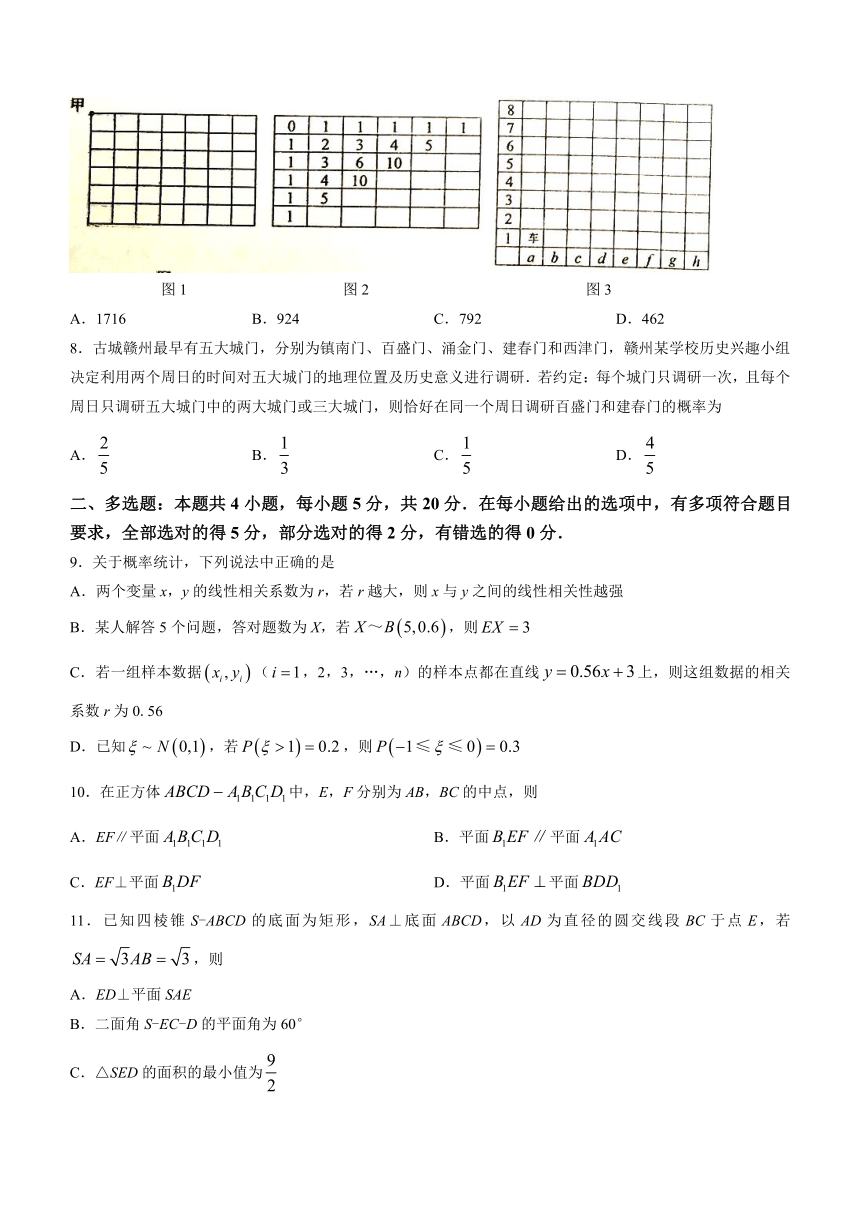
7.“杨辉三角”出自我国数学家杨辉1261年著的《详解九章算法》一书,393年后欧洲帕斯卡也发现这个三角图形,所以“杨辉三角”也叫做“帕斯卡三角形”,它结构优美、性质奇特,生活中很多问题都与杨辉三角有着或多或少的联系.例如生活中的最短路径问题:如图1所示,从甲到每一个交叉点的走法最短路径的条数(图2)与杨辉三角中对应的数性质相同.已知图3是国际象棋简易棋盘,现有一棋子“车”的起始位置是“a1”,则它要到“g7”位置的最短路径的条数为
图1 图2 图3
A.1716 B.924 C.792 D.462
8.古城赣州最早有五大城门,分别为镇南门、百盛门、涌金门、建春门和西津门,赣州某学校历史兴趣小组决定利用两个周日的时间对五大城门的地理位置及历史意义进行调研.若约定:每个城门只调研一次,且每个周日只调研五大城门中的两大城门或三大城门,则恰好在同一个周日调研百盛门和建春门的概率为
A. B. C. D.
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有错选的得0分.
9.关于概率统计,下列说法中正确的是
A.两个变量x,y的线性相关系数为r,若r越大,则x与y之间的线性相关性越强
B.某人解答5个问题,答对题数为X,若,则
C.若一组样本数据(,2,3,…,n)的样本点都在直线上,则这组数据的相关系数r为0.56
D.已知,若,则
10.在正方体中,E,F分别为AB,BC的中点,则
A.EF∥平面 B.平面平面
C.EF⊥平面 D.平面平面
11.已知四棱锥S-ABCD的底面为矩形,SA⊥底面ABCD,以AD为直径的圆交线段BC于点E,若,则
A.ED⊥平面SAE
B.二面角S-EC-D的平面角为60°
C.△SED的面积的最小值为
D.存在某个位置E,使得点A到平面SED的距离为
12.已知圆:(),这些圆的全体构成集合,则
A.x轴截圆所得的弦长为2
B.对任意正整数k,圆内含于圆
C.任意正实数m,存在,使得圆与直线有交点
D.存在正实数m,使得A中与直线相交的圆有且仅有2024个
第Ⅱ卷(非选择题共90分)
三、填空题:本大题共4小题,每小题5分,共20分.
13.展开式中的常数项为 .
14.在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,,E为PC的中点,则直线PC与平面BDE所成角的正弦值为 .
15.某学校物理兴趣小组有6个男生,4个女生,历史兴趣小组有5个男生,7个女生,先从两个兴趣小组中随机选取一个兴趣小组,再从所取的兴趣小组中随机抽取一个学生,则该学生是男生的概率是 .
16.已知,为椭圆C:的焦点,过的直线l与C交A,B两点,则的内切圆面积最大值为 .
四、解答题:共70分,解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
大气污染物(直径不大于2.5的颗粒物)的浓度超过一定限度会影响人的身体健康.为研究浓度y(单位:)与汽车流量x(单位:千辆)的线性关系,研究人员选定了10个城市,在每个城市建立交通监测点,统计了24h内过往的汽车流量以及同时段空气中的浓度,得到如下数据:
城市编号 1 2 3 4 5 6 7 8 9 10 总和
x 1.300 1.444 0.786 1.652 1.756 1.754 1.200 1.500 1.200 0.908 13.5
y 66 76 21 170 156 120 72 120 100 129 1030
并计算得,,.
(1)求变量y关于x的线性回归方程;
(2)根据24h内浓度确定空气质量等级,浓度在0~35为优,35~75为良,75~115为轻度污染,115~150为中度污染,150~250为重度污染,已知某城市24h内过往的汽车流量为1360辆,判断该城市的空气质量等级.
参考公式:线性回归方程为,其中以.
18.(本小题满分12分)
已知圆C:,点.
(1)若,过P的直线l与C相切,求l的方程;
(2)若C上存在到P的距离为1的点,求m的取值范围.
19.(本小题满分12分)
甲、乙、丙三位同学进行乒乓球比赛,每局比赛两人对战,另一人轮空,没有平局.每局胜者与此局轮空者进行下一局的比赛.约定先赢两局者获胜,比赛随即结束.已知每局比赛甲胜乙的概率为,甲胜丙的概率为,乙胜丙的概率为.
(1)若第一局由乙丙对战,求甲获胜的概率;
(2)判断并说明由哪两位同学进行首场对战才能使甲获胜的概率最大.
20.(本小题满分12分)
现有一种趣味答题比赛,其比赛规则如下:①每位参赛者最多参加5轮比赛;②每一轮比赛中,参赛选手从10道题中随机抽取4道回答,每答对一道题积2分,答错或放弃均积0分;③每一轮比赛中,获得积分至少6分的选手将获得“挑战达人”勋章一枚;④结束所有轮比赛后,参赛选手还可以凭总积分获得相对应的礼品.据主办方透露:这10道题中有7道题是大家都会做的,有3道题是大家都不会做的.
(1)求某参赛选手在一轮比赛中所获得积分X的分布列和期望;
(2)若参赛选手每轮获得勋章的概率稳定且每轮是否获得勋章相互独立.问:某参赛选手在5轮参赛中,获得多少枚“挑战达人”勋章的概率最大?
21.(本小题满分12分)
如图,在多面体ABCDEF中,四边形CDEF为正方形,,AB∥EF,.
(1)设平面平面,证明:l∥CF;
(2)直线DE上是否存在点G,使得DE⊥平面ABG?若存在,确定G的位置并说明理由;
(3)若,,求平面BFG与平面DEA夹角的余弦的取值范围.
22.(本小题满分12分)
已知椭圆C:()的离心率为,直线l:是椭圆C与圆:的一条公切线.
(1)求椭圆C的方程;
(2)若点为椭圆C的一点,直线:交圆于M,N两点,以M,N为切点分别作圆的切线,两条切线交于点Q,证明:为定值.
赣州市2023~2024学年度第一学期期末考试
高二数学试卷参考答案
2024年1月
一、单选题:(本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
题号 1 2 3 4 5 6 7 8
选项 C B B D C A B A
二、多选题:(本题共4小题,每小题5分,共20分,在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有错选的得0分)
题号 9 10 11 12
选项 BD AD ABD ACD
三、填空题:(本大题共4小题,每小题5分,共20分)
13.15 14. 15. 16.
17.解:
(1)由题意得,
又因为,
所以
所以
所以变量y关于x的线性回归方程为.
(2)当辆千辆时,可得
因为
所以该城市的空气质量等级为轻度污染.
18.解:
(1)因为,所以圆C的方程为
①当l的斜率不存在时,l的方程为,与圆C相切,符合题意
②当l的斜率存在时,设l的方程为,即
圆心C到l的距离,解得
则l的方程为,即
综上可得,l的方程为或.
(2)由题意可得圆C:,圆心,半径
则圆心C到的距离
要使C上存在到P的距离为1的点
则,即,
解得
所以m的取值范围为.
19.解:
(1)第一局由乙丙对战,甲获胜有两种情况:
①乙丙对战乙胜,乙甲对战甲胜,甲丙对战甲胜,则概率为
②乙丙对战丙胜,丙甲对战甲胜,甲乙对战甲胜,则概率为
综上,甲获胜的概率为
(2)若第一局乙丙对战,由(1)知甲获胜的概率为
若第一局甲乙对战,则甲获胜有三种情况:
①甲乙对战甲胜,甲丙对战甲胜,概率为
②甲乙对战甲胜,甲丙对战丙胜,丙乙对战乙胜,乙甲对战甲胜的概率为
③甲乙对战乙胜,乙丙对战丙胜,丙甲对战甲胜,乙甲对战甲胜的概率为
所以最终甲获胜的概率为;
若第一局甲丙对战,则甲获胜也有三种情况:
①甲丙对战甲胜,甲乙对战甲胜的概率为
②甲丙对战甲胜,甲乙对战乙胜,乙丙对战丙胜,丙甲对战甲胜的概率为
③甲丙对战丙胜,丙乙对战乙胜,乙甲对战甲胜,甲丙对战甲胜的概率为
所以最终甲获胜的概率为
因为
所以第一局甲乙对战才能使甲获胜的概率最大.
20.解:
(1)由题知:X可取2,4,6,8,则
故X的分布列为
X 2 4 6 8
P
则X的期望
(2)由(1)知参赛选手在一轮比赛中获得“挑战达人”勋章的概率为
则某参赛选手在5轮挑战比赛中,记获得“挑战达人”勋章的枚数为Y,则
故(,1,…,5)
∴假设当时,概率最大,则
解得,而
故某参赛选手在5轮挑战比赛中,获得3枚或4枚“挑战达人”勋章的概率最大.
另法:由(1)知参赛选手在一轮获得“挑战达人”勋章的概率为
某参赛选手在5轮挑战比赛中,获得“挑战达人”勋章的枚数为Y,则
故(,1,…,5)
所以Y的分布列为
Y 0 1 2 3 4 5
P
从分布列中可以看出,概率最大为
所以参赛选手在5轮挑战比赛中,获得3枚或4枚“挑战达人”勋章的概率最大.
21.
(1)证明:因为四边形CDEF为矩形,所以CF∥DE
平面ADE,平面ADE,所以CF∥平面ADE
又平面平面,平面BCF,所以CF∥l
(2)解:存在G为DE中点,使得DE⊥平面ABG
因为,则AG⊥DE
又EF∥AB且EF⊥DE,所以AB⊥DE,故DE⊥平面ABG
(3)解:设点H为DE中点,取EF和FC和AB中点为P,Q,S
由(2)知,E,F,H,Q共面且DE⊥平面ABH,取DF与CE连线交于O点,连OS
则DE⊥OS,易知ABQH为等腰梯形,所以
建立如图示的空间直角坐标系O-xyz,则,,,
又,所以
设AB到平面DCFE的距离为h,因为四边形ABFE和四边形CDAB为两个全等的等腰梯形
所以EF∥AB,设,,又
所以,解得
所以,,又,,,
令,
所以
设平面BFG的法向量为,由和,
即,取,得
设平面DEA的法向量为由和
即,取,得
所以
令,则,
则
令,则,
所以在上单调递增,
又当时,;当时,
所以,
所以,
所以平面BFG和平面DEA的夹角的余弦值的取值范围为.
22.解:
(1)因为离心率
所以
因为
是圆:的一条切线,所以
所以
由,可得
因为是椭圆的一条切线
所以
结合,解得
所以椭圆C的方程为.
(2)设点,,,则,
因为M,N为直线QM,QN与圆的切点
所以,
所以直线QM的方程为:,即,即
直线QN的方程为:,即,即
所以点Q满足,即.
所以直线MN的方程为
又因为M,N为直线与圆的交点
所以MN的方程为,即
所以恒成立
所以,即
所以
又因为点为椭圆C上一点,所以
所以为定值.
高二数学试卷
2024年1月
第Ⅰ卷(选择题共60分)
一、单选题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.直线的倾斜角为
A.30° B.60° C.120° D.150°
2.“”是“方程表示的曲线是椭圆”的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
3.已知直线:和:.若,则m的值为
A. B.3 C.1或3 D.或3
4.阅读课上,5名同学分别从3种不同的书中选择一种进行阅读,不同的选法种数是
A.50 B.60 C.125 D.243
5.设F为抛物线C:的焦点,A为平面内定点,若抛物线C上存在点P使得的最小值为5,则点A可以为
A. B. C. D.
6.已知,为双曲线C:(,)的两个焦点,以为直径的圆与C在第一象限的交点为P.若,则C的离心率为
A. B. C. D.
7.“杨辉三角”出自我国数学家杨辉1261年著的《详解九章算法》一书,393年后欧洲帕斯卡也发现这个三角图形,所以“杨辉三角”也叫做“帕斯卡三角形”,它结构优美、性质奇特,生活中很多问题都与杨辉三角有着或多或少的联系.例如生活中的最短路径问题:如图1所示,从甲到每一个交叉点的走法最短路径的条数(图2)与杨辉三角中对应的数性质相同.已知图3是国际象棋简易棋盘,现有一棋子“车”的起始位置是“a1”,则它要到“g7”位置的最短路径的条数为
图1 图2 图3
A.1716 B.924 C.792 D.462
8.古城赣州最早有五大城门,分别为镇南门、百盛门、涌金门、建春门和西津门,赣州某学校历史兴趣小组决定利用两个周日的时间对五大城门的地理位置及历史意义进行调研.若约定:每个城门只调研一次,且每个周日只调研五大城门中的两大城门或三大城门,则恰好在同一个周日调研百盛门和建春门的概率为
A. B. C. D.
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有错选的得0分.
9.关于概率统计,下列说法中正确的是
A.两个变量x,y的线性相关系数为r,若r越大,则x与y之间的线性相关性越强
B.某人解答5个问题,答对题数为X,若,则
C.若一组样本数据(,2,3,…,n)的样本点都在直线上,则这组数据的相关系数r为0.56
D.已知,若,则
10.在正方体中,E,F分别为AB,BC的中点,则
A.EF∥平面 B.平面平面
C.EF⊥平面 D.平面平面
11.已知四棱锥S-ABCD的底面为矩形,SA⊥底面ABCD,以AD为直径的圆交线段BC于点E,若,则
A.ED⊥平面SAE
B.二面角S-EC-D的平面角为60°
C.△SED的面积的最小值为
D.存在某个位置E,使得点A到平面SED的距离为
12.已知圆:(),这些圆的全体构成集合,则
A.x轴截圆所得的弦长为2
B.对任意正整数k,圆内含于圆
C.任意正实数m,存在,使得圆与直线有交点
D.存在正实数m,使得A中与直线相交的圆有且仅有2024个
第Ⅱ卷(非选择题共90分)
三、填空题:本大题共4小题,每小题5分,共20分.
13.展开式中的常数项为 .
14.在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,,E为PC的中点,则直线PC与平面BDE所成角的正弦值为 .
15.某学校物理兴趣小组有6个男生,4个女生,历史兴趣小组有5个男生,7个女生,先从两个兴趣小组中随机选取一个兴趣小组,再从所取的兴趣小组中随机抽取一个学生,则该学生是男生的概率是 .
16.已知,为椭圆C:的焦点,过的直线l与C交A,B两点,则的内切圆面积最大值为 .
四、解答题:共70分,解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
大气污染物(直径不大于2.5的颗粒物)的浓度超过一定限度会影响人的身体健康.为研究浓度y(单位:)与汽车流量x(单位:千辆)的线性关系,研究人员选定了10个城市,在每个城市建立交通监测点,统计了24h内过往的汽车流量以及同时段空气中的浓度,得到如下数据:
城市编号 1 2 3 4 5 6 7 8 9 10 总和
x 1.300 1.444 0.786 1.652 1.756 1.754 1.200 1.500 1.200 0.908 13.5
y 66 76 21 170 156 120 72 120 100 129 1030
并计算得,,.
(1)求变量y关于x的线性回归方程;
(2)根据24h内浓度确定空气质量等级,浓度在0~35为优,35~75为良,75~115为轻度污染,115~150为中度污染,150~250为重度污染,已知某城市24h内过往的汽车流量为1360辆,判断该城市的空气质量等级.
参考公式:线性回归方程为,其中以.
18.(本小题满分12分)
已知圆C:,点.
(1)若,过P的直线l与C相切,求l的方程;
(2)若C上存在到P的距离为1的点,求m的取值范围.
19.(本小题满分12分)
甲、乙、丙三位同学进行乒乓球比赛,每局比赛两人对战,另一人轮空,没有平局.每局胜者与此局轮空者进行下一局的比赛.约定先赢两局者获胜,比赛随即结束.已知每局比赛甲胜乙的概率为,甲胜丙的概率为,乙胜丙的概率为.
(1)若第一局由乙丙对战,求甲获胜的概率;
(2)判断并说明由哪两位同学进行首场对战才能使甲获胜的概率最大.
20.(本小题满分12分)
现有一种趣味答题比赛,其比赛规则如下:①每位参赛者最多参加5轮比赛;②每一轮比赛中,参赛选手从10道题中随机抽取4道回答,每答对一道题积2分,答错或放弃均积0分;③每一轮比赛中,获得积分至少6分的选手将获得“挑战达人”勋章一枚;④结束所有轮比赛后,参赛选手还可以凭总积分获得相对应的礼品.据主办方透露:这10道题中有7道题是大家都会做的,有3道题是大家都不会做的.
(1)求某参赛选手在一轮比赛中所获得积分X的分布列和期望;
(2)若参赛选手每轮获得勋章的概率稳定且每轮是否获得勋章相互独立.问:某参赛选手在5轮参赛中,获得多少枚“挑战达人”勋章的概率最大?
21.(本小题满分12分)
如图,在多面体ABCDEF中,四边形CDEF为正方形,,AB∥EF,.
(1)设平面平面,证明:l∥CF;
(2)直线DE上是否存在点G,使得DE⊥平面ABG?若存在,确定G的位置并说明理由;
(3)若,,求平面BFG与平面DEA夹角的余弦的取值范围.
22.(本小题满分12分)
已知椭圆C:()的离心率为,直线l:是椭圆C与圆:的一条公切线.
(1)求椭圆C的方程;
(2)若点为椭圆C的一点,直线:交圆于M,N两点,以M,N为切点分别作圆的切线,两条切线交于点Q,证明:为定值.
赣州市2023~2024学年度第一学期期末考试
高二数学试卷参考答案
2024年1月
一、单选题:(本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
题号 1 2 3 4 5 6 7 8
选项 C B B D C A B A
二、多选题:(本题共4小题,每小题5分,共20分,在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有错选的得0分)
题号 9 10 11 12
选项 BD AD ABD ACD
三、填空题:(本大题共4小题,每小题5分,共20分)
13.15 14. 15. 16.
17.解:
(1)由题意得,
又因为,
所以
所以
所以变量y关于x的线性回归方程为.
(2)当辆千辆时,可得
因为
所以该城市的空气质量等级为轻度污染.
18.解:
(1)因为,所以圆C的方程为
①当l的斜率不存在时,l的方程为,与圆C相切,符合题意
②当l的斜率存在时,设l的方程为,即
圆心C到l的距离,解得
则l的方程为,即
综上可得,l的方程为或.
(2)由题意可得圆C:,圆心,半径
则圆心C到的距离
要使C上存在到P的距离为1的点
则,即,
解得
所以m的取值范围为.
19.解:
(1)第一局由乙丙对战,甲获胜有两种情况:
①乙丙对战乙胜,乙甲对战甲胜,甲丙对战甲胜,则概率为
②乙丙对战丙胜,丙甲对战甲胜,甲乙对战甲胜,则概率为
综上,甲获胜的概率为
(2)若第一局乙丙对战,由(1)知甲获胜的概率为
若第一局甲乙对战,则甲获胜有三种情况:
①甲乙对战甲胜,甲丙对战甲胜,概率为
②甲乙对战甲胜,甲丙对战丙胜,丙乙对战乙胜,乙甲对战甲胜的概率为
③甲乙对战乙胜,乙丙对战丙胜,丙甲对战甲胜,乙甲对战甲胜的概率为
所以最终甲获胜的概率为;
若第一局甲丙对战,则甲获胜也有三种情况:
①甲丙对战甲胜,甲乙对战甲胜的概率为
②甲丙对战甲胜,甲乙对战乙胜,乙丙对战丙胜,丙甲对战甲胜的概率为
③甲丙对战丙胜,丙乙对战乙胜,乙甲对战甲胜,甲丙对战甲胜的概率为
所以最终甲获胜的概率为
因为
所以第一局甲乙对战才能使甲获胜的概率最大.
20.解:
(1)由题知:X可取2,4,6,8,则
故X的分布列为
X 2 4 6 8
P
则X的期望
(2)由(1)知参赛选手在一轮比赛中获得“挑战达人”勋章的概率为
则某参赛选手在5轮挑战比赛中,记获得“挑战达人”勋章的枚数为Y,则
故(,1,…,5)
∴假设当时,概率最大,则
解得,而
故某参赛选手在5轮挑战比赛中,获得3枚或4枚“挑战达人”勋章的概率最大.
另法:由(1)知参赛选手在一轮获得“挑战达人”勋章的概率为
某参赛选手在5轮挑战比赛中,获得“挑战达人”勋章的枚数为Y,则
故(,1,…,5)
所以Y的分布列为
Y 0 1 2 3 4 5
P
从分布列中可以看出,概率最大为
所以参赛选手在5轮挑战比赛中,获得3枚或4枚“挑战达人”勋章的概率最大.
21.
(1)证明:因为四边形CDEF为矩形,所以CF∥DE
平面ADE,平面ADE,所以CF∥平面ADE
又平面平面,平面BCF,所以CF∥l
(2)解:存在G为DE中点,使得DE⊥平面ABG
因为,则AG⊥DE
又EF∥AB且EF⊥DE,所以AB⊥DE,故DE⊥平面ABG
(3)解:设点H为DE中点,取EF和FC和AB中点为P,Q,S
由(2)知,E,F,H,Q共面且DE⊥平面ABH,取DF与CE连线交于O点,连OS
则DE⊥OS,易知ABQH为等腰梯形,所以
建立如图示的空间直角坐标系O-xyz,则,,,
又,所以
设AB到平面DCFE的距离为h,因为四边形ABFE和四边形CDAB为两个全等的等腰梯形
所以EF∥AB,设,,又
所以,解得
所以,,又,,,
令,
所以
设平面BFG的法向量为,由和,
即,取,得
设平面DEA的法向量为由和
即,取,得
所以
令,则,
则
令,则,
所以在上单调递增,
又当时,;当时,
所以,
所以,
所以平面BFG和平面DEA的夹角的余弦值的取值范围为.
22.解:
(1)因为离心率
所以
因为
是圆:的一条切线,所以
所以
由,可得
因为是椭圆的一条切线
所以
结合,解得
所以椭圆C的方程为.
(2)设点,,,则,
因为M,N为直线QM,QN与圆的切点
所以,
所以直线QM的方程为:,即,即
直线QN的方程为:,即,即
所以点Q满足,即.
所以直线MN的方程为
又因为M,N为直线与圆的交点
所以MN的方程为,即
所以恒成立
所以,即
所以
又因为点为椭圆C上一点,所以
所以为定值.
同课章节目录
