2015年快乐暑假初三升初四衔接复习部分——正方形(含答案)
文档属性
| 名称 | 2015年快乐暑假初三升初四衔接复习部分——正方形(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 109.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-07-15 00:00:00 | ||
图片预览

文档简介
2015年快乐暑假初三升初四衔接复习——正方形(含答案)
一、知识梳理
知识点1:正方形的性质和判定
1、正方形的 , ;
2、正方形的对角线 。
3、 的菱形是正方形。4、 的菱形是正方形。
5、 的矩形是正方形。6、 的矩形是正方形。
二、典例解析
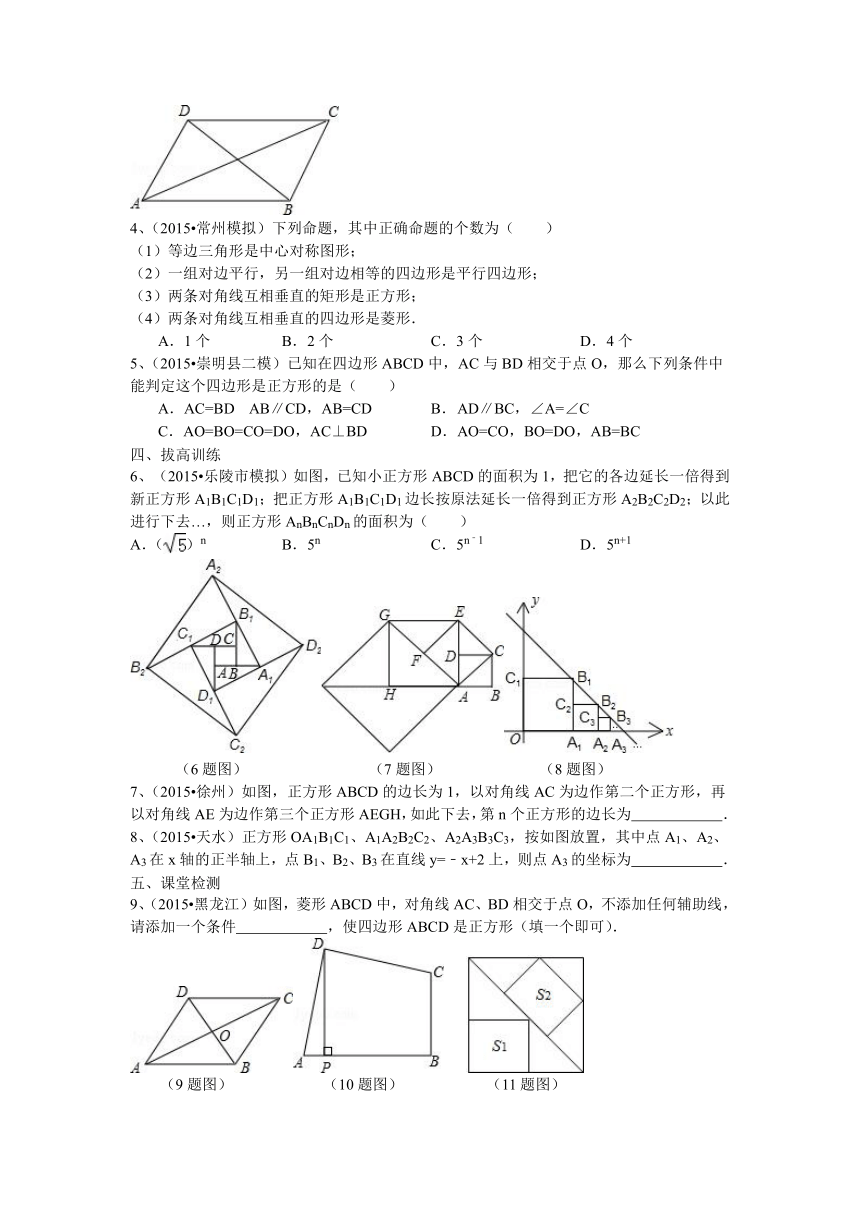
1、(2015 荆州)如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
2、(2015 北塘区二模)如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
(1)求证:AB⊥AE.
(2)若点D为AB中点,求证:四边形ADCE是正方形.
巩固提升
3、(2015 日照)小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使 ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
A.①② B. ②③ C. ①③ D. ②④
4、(2015 常州模拟)下列命题,其中正确命题的个数为( )
(1)等边三角形是中心对称图形;
(2)一组对边平行,另一组对边相等的四边形是平行四边形;
(3)两条对角线互相垂直的矩形是正方形;
(4)两条对角线互相垂直的四边形是菱形.
A.1个 B. 2个 C. 3个 D. 4个
5、(2015 崇明县二模)已知在四边形ABCD中,AC与BD相交于点O,那么下列条件中能判定这个四边形是正方形的是( )
A.AC=BD AB∥CD,AB=CD B. AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD D. AO=CO,BO=DO,AB=BC
拔高训练
(2015 乐陵市模拟)如图,已知小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1;把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2;以此进行下去…,则正方形AnBnCnDn的面积为( )
A.()n B. 5n C. 5n﹣1 D. 5n+1
(6题图) (7题图) (8题图)
7、(2015 徐州)如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第n个正方形的边长为 .
8、(2015 天水)正方形OA1B1C1、A1A2B2C2、A2A3B3C3,按如图放置,其中点A1、A2、A3在x轴的正半轴上,点B1、B2、B3在直线y=﹣x+2上,则点A3的坐标为 .
五、课堂检测
9、(2015 黑龙江)如图,菱形ABCD中,对角线AC、BD相交于点O,不添加任何辅助线,请添加一个条件 ,使四边形ABCD是正方形(填一个即可).
(9题图) (10题图) (11题图)
(2015春 启东市模拟)如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是 .
11、(2013 菏泽)如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为( )
A.16 B.17 C.18 D.19
(12) (13)
12、(2014 宜宾)如图,将n个边长都为2的正方形按如图所示摆放,点A1,A2,…An分别是正方形的中心,则这n个正方形重叠部分的面积之和是( )
A.n B.n﹣1 C.()n﹣1 D.n
13、(2014 苏州模拟)如图,四边形ABCD中,E,F,G,H分别是边AB、BC、CD、DA的中点.若四边形EFGH为菱形,则对角线AC、BD应满足条件 _________ .
14、(2015 鄂州)如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE,CE.
(1)求证:BE=CE.
(2)求∠BEC的度数.
15、(2013 湘潭)在数学活动课中,小辉将边长为和3的两个正方形放置在直线l上,如图1,他连结AD、CF,经测量发现AD=CF.
(1)他将正方形ODEF绕O点逆时针旋转一定的角度,如图2,试判断AD与CF还相等吗?说明你的理由;
(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图3,请你求出CF的长.
2015年快乐暑假初三升初四衔接复习——正方形参考答案
1、(1)证明:在正方形ABCD中,AB=BC,∠ABP=∠CBP=45°,
在△ABP和△CBP中,,∴△ABP≌△CBP(SAS),∴PA=PC,
∵PA=PE,∴PC=PE;
(2)由(1)知,△ABP≌△CBP,∴∠BAP=∠BCP,∴∠DAP=∠DCP,
∵PA=PC,∴∠DAP=∠E,∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,即∠CPF=∠EDF=90°;
(3)在正方形ABCD中,AB=BC,∠ABP=∠CBP=45°,∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP,
∵PA=PE,∴PC=PE,∴∠DAP=∠DCP,
∵PA=PC,∴∠DAP=∠E,∴∠DCP=∠E
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPF=∠EDF=180°﹣∠ADC=180°﹣120°=60°,
∴△EPC是等边三角形,∴PC=CE,∴AP=CE;
2、(1)解:∵∠ACB=90°,∴∠BCD+∠ACD=90°,
∵∠DCE=90°,∴∠ACD+∠ACE=90°,∴∠BCD=∠ACE,
在△CBD与△CAE中,∵,∴△CBD≌△CAE(SAS),∴∠B=∠CAE,
∵∠B+∠BAC=90°,∴∠BAC+∠EAC=90°,∴AB⊥AE;
(2)证明:∵点D为AB中点,∴∠ADC=90°,
∵∠DCE=90°,∠BAE=90°,∴四边形ADCE是矩形,
∴CD=CE,∴四边形ADCE是正方形.
B 4、A 5、C 6、B 7、()n﹣1 8、(,0)
∠BAD=90° 10、 3 11.B.12.B.13. AC=BD
14、(1)证明:∵四边形ABCD为正方形∴AB=AD=CD,∠BAD=∠ADC=90°
∵三角形ADE为正三角形∴AE=AD=DE,∠EAD=∠EDA=60°
∴∠BAE=∠CDE=150°
在△BAE和△CDE中,∴△BAE≌△CDE∴BE=CE;
(2)∵AB=AD,AD=AE,∴AB=AE,∴∠ABE=∠AEB,
又∵∠BAE=150°,∴∠ABE=∠AEB=15°,
同理:∠CED=15°
∴∠BEC=60°﹣15°×2=30°.
15、解:(1)AD=CF.
理由如下:在正方形ABCO和正方形ODEF中,AO=CO,OD=OF,∠AOC=∠DOF=90°,
∴∠AOC+∠COD=∠DOF+∠COD,
即∠AOD=∠COF,
在△AOD和△COF中,,∴△AOD≌△COF(SAS),∴AD=CF;
(2)与(1)同理求出CF=AD,
如图,连接DF交OE于G,则DF⊥OE,DG=OG=OE,
∵正方形ODEF的边长为,
∴OE=OD=×=2,∴DG=OG=OE=×2=1,∴AG=AO+OG=3+1=4,
在Rt△ADG中,AD===,∴CF=AD=.
一、知识梳理
知识点1:正方形的性质和判定
1、正方形的 , ;
2、正方形的对角线 。
3、 的菱形是正方形。4、 的菱形是正方形。
5、 的矩形是正方形。6、 的矩形是正方形。
二、典例解析
1、(2015 荆州)如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
2、(2015 北塘区二模)如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
(1)求证:AB⊥AE.
(2)若点D为AB中点,求证:四边形ADCE是正方形.
巩固提升
3、(2015 日照)小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使 ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
A.①② B. ②③ C. ①③ D. ②④
4、(2015 常州模拟)下列命题,其中正确命题的个数为( )
(1)等边三角形是中心对称图形;
(2)一组对边平行,另一组对边相等的四边形是平行四边形;
(3)两条对角线互相垂直的矩形是正方形;
(4)两条对角线互相垂直的四边形是菱形.
A.1个 B. 2个 C. 3个 D. 4个
5、(2015 崇明县二模)已知在四边形ABCD中,AC与BD相交于点O,那么下列条件中能判定这个四边形是正方形的是( )
A.AC=BD AB∥CD,AB=CD B. AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD D. AO=CO,BO=DO,AB=BC
拔高训练
(2015 乐陵市模拟)如图,已知小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1;把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2;以此进行下去…,则正方形AnBnCnDn的面积为( )
A.()n B. 5n C. 5n﹣1 D. 5n+1
(6题图) (7题图) (8题图)
7、(2015 徐州)如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第n个正方形的边长为 .
8、(2015 天水)正方形OA1B1C1、A1A2B2C2、A2A3B3C3,按如图放置,其中点A1、A2、A3在x轴的正半轴上,点B1、B2、B3在直线y=﹣x+2上,则点A3的坐标为 .
五、课堂检测
9、(2015 黑龙江)如图,菱形ABCD中,对角线AC、BD相交于点O,不添加任何辅助线,请添加一个条件 ,使四边形ABCD是正方形(填一个即可).
(9题图) (10题图) (11题图)
(2015春 启东市模拟)如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是 .
11、(2013 菏泽)如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为( )
A.16 B.17 C.18 D.19
(12) (13)
12、(2014 宜宾)如图,将n个边长都为2的正方形按如图所示摆放,点A1,A2,…An分别是正方形的中心,则这n个正方形重叠部分的面积之和是( )
A.n B.n﹣1 C.()n﹣1 D.n
13、(2014 苏州模拟)如图,四边形ABCD中,E,F,G,H分别是边AB、BC、CD、DA的中点.若四边形EFGH为菱形,则对角线AC、BD应满足条件 _________ .
14、(2015 鄂州)如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE,CE.
(1)求证:BE=CE.
(2)求∠BEC的度数.
15、(2013 湘潭)在数学活动课中,小辉将边长为和3的两个正方形放置在直线l上,如图1,他连结AD、CF,经测量发现AD=CF.
(1)他将正方形ODEF绕O点逆时针旋转一定的角度,如图2,试判断AD与CF还相等吗?说明你的理由;
(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图3,请你求出CF的长.
2015年快乐暑假初三升初四衔接复习——正方形参考答案
1、(1)证明:在正方形ABCD中,AB=BC,∠ABP=∠CBP=45°,
在△ABP和△CBP中,,∴△ABP≌△CBP(SAS),∴PA=PC,
∵PA=PE,∴PC=PE;
(2)由(1)知,△ABP≌△CBP,∴∠BAP=∠BCP,∴∠DAP=∠DCP,
∵PA=PC,∴∠DAP=∠E,∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,即∠CPF=∠EDF=90°;
(3)在正方形ABCD中,AB=BC,∠ABP=∠CBP=45°,∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP,
∵PA=PE,∴PC=PE,∴∠DAP=∠DCP,
∵PA=PC,∴∠DAP=∠E,∴∠DCP=∠E
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPF=∠EDF=180°﹣∠ADC=180°﹣120°=60°,
∴△EPC是等边三角形,∴PC=CE,∴AP=CE;
2、(1)解:∵∠ACB=90°,∴∠BCD+∠ACD=90°,
∵∠DCE=90°,∴∠ACD+∠ACE=90°,∴∠BCD=∠ACE,
在△CBD与△CAE中,∵,∴△CBD≌△CAE(SAS),∴∠B=∠CAE,
∵∠B+∠BAC=90°,∴∠BAC+∠EAC=90°,∴AB⊥AE;
(2)证明:∵点D为AB中点,∴∠ADC=90°,
∵∠DCE=90°,∠BAE=90°,∴四边形ADCE是矩形,
∴CD=CE,∴四边形ADCE是正方形.
B 4、A 5、C 6、B 7、()n﹣1 8、(,0)
∠BAD=90° 10、 3 11.B.12.B.13. AC=BD
14、(1)证明:∵四边形ABCD为正方形∴AB=AD=CD,∠BAD=∠ADC=90°
∵三角形ADE为正三角形∴AE=AD=DE,∠EAD=∠EDA=60°
∴∠BAE=∠CDE=150°
在△BAE和△CDE中,∴△BAE≌△CDE∴BE=CE;
(2)∵AB=AD,AD=AE,∴AB=AE,∴∠ABE=∠AEB,
又∵∠BAE=150°,∴∠ABE=∠AEB=15°,
同理:∠CED=15°
∴∠BEC=60°﹣15°×2=30°.
15、解:(1)AD=CF.
理由如下:在正方形ABCO和正方形ODEF中,AO=CO,OD=OF,∠AOC=∠DOF=90°,
∴∠AOC+∠COD=∠DOF+∠COD,
即∠AOD=∠COF,
在△AOD和△COF中,,∴△AOD≌△COF(SAS),∴AD=CF;
(2)与(1)同理求出CF=AD,
如图,连接DF交OE于G,则DF⊥OE,DG=OG=OE,
∵正方形ODEF的边长为,
∴OE=OD=×=2,∴DG=OG=OE=×2=1,∴AG=AO+OG=3+1=4,
在Rt△ADG中,AD===,∴CF=AD=.
