2023-2024学年度人教版数学七年级下册5.2.2平行线的判定 课件(共28张PPT)
文档属性
| 名称 | 2023-2024学年度人教版数学七年级下册5.2.2平行线的判定 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 661.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-28 12:27:48 | ||
图片预览




文档简介
(共28张PPT)
5.2.2 平行线的判定
1. 掌握平行线的三种判定方法;
2. 会用判定方法来判断两条直线是否平行.
学习目标
重点
难点
新课引入
根据平行线的定义,如果平面内的两条直线不相交,就可以判断这两条直线平行.但是,由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据定义来判断两条直线是否平行,那么,有没有其他判定方法呢?
新知学习
思考
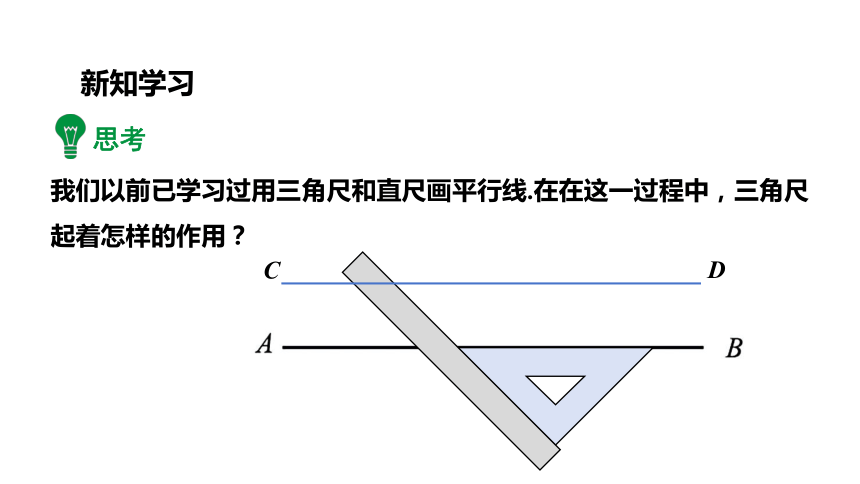
我们以前已学习过用三角尺和直尺画平行线.在在这一过程中,三角尺起着怎样的作用?
C
D
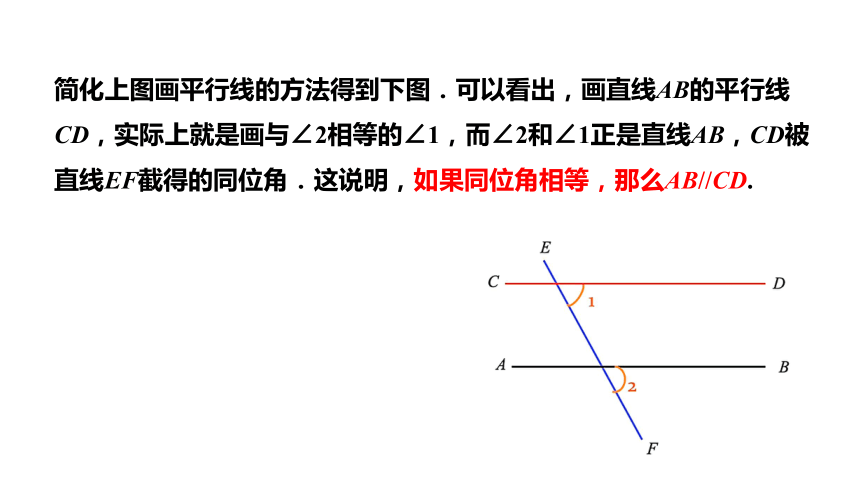
简化上图画平行线的方法得到下图.可以看出,画直线AB的平行线CD,实际上就是画与∠2相等的∠1,而∠2和∠1正是直线AB,CD被直线EF截得的同位角.这说明,如果同位角相等,那么AB//CD.
归纳
一般地,有如下利用同位角判定两条直线平行的方法:
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
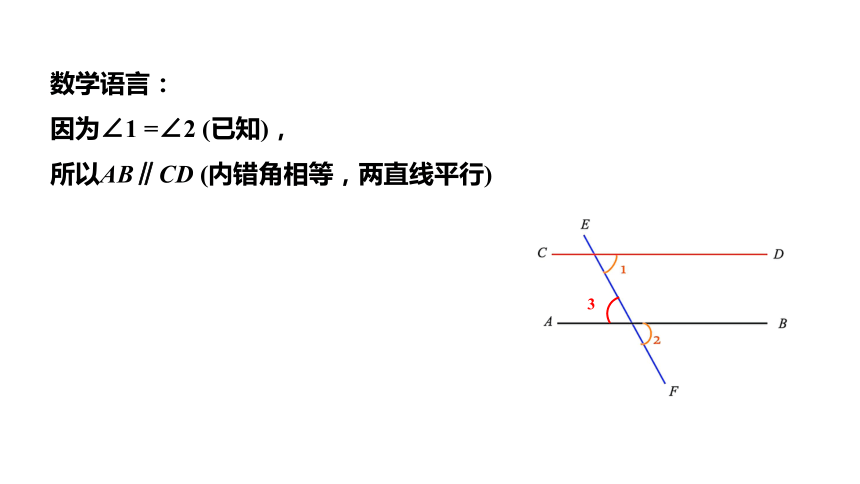
数学语言:
因为∠1 =∠2 (已知),
所以AB∥CD (内错角相等,两直线平行)
3
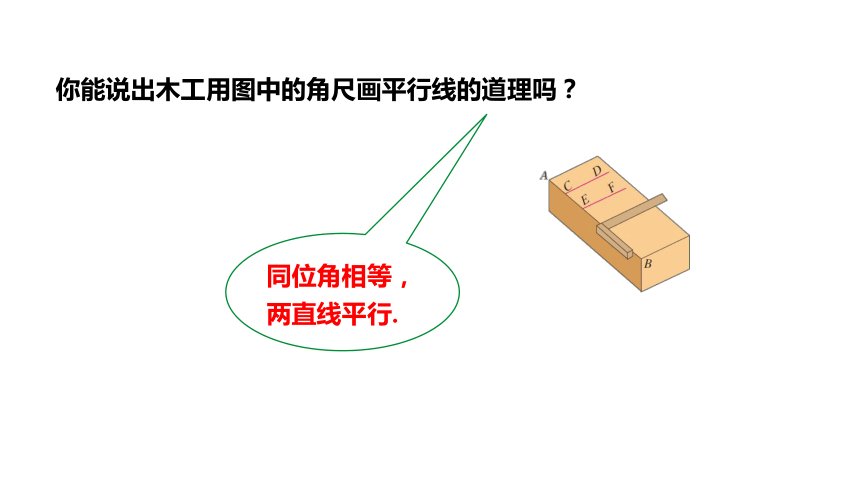
你能说出木工用图中的角尺画平行线的道理吗?
同位角相等,
两直线平行.
思考
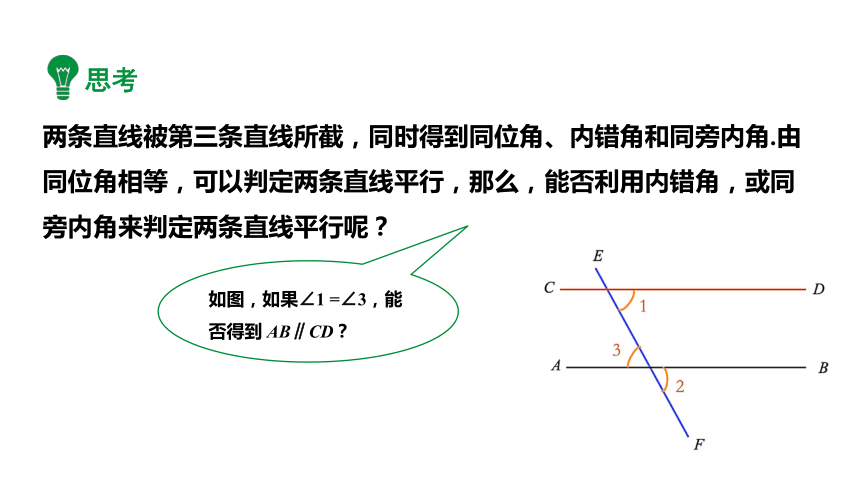
如图,如果∠1 =∠3,能否得到 AB∥CD?
两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角.由同位角相等,可以判定两条直线平行,那么,能否利用内错角,或同旁内角来判定两条直线平行呢?
猜想:直线 AB,CD 被直线 EF 所截,如果∠1 =∠3,那么 AB∥CD.
推理:因为∠1 =∠3
而∠2 =∠3 (对顶角相等),
所以∠1 =∠2
所以AB∥CD (同位角相等,两直线平行).
归纳
由判定方法1,可以得出利用内错角判定两条直线平行的方法:
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
数学语言:
∵∠1 =∠3 (已知),
∴AB∥CD (内错角相等,两直线平行)
3
如图,∠1 和∠4 满足什么关系时,能得到 AB∥CD?
思考
猜想:直线 AB,CD 被直线 EF 所截,如果∠1 +∠4 = 180°,那么AB∥CD.
分析:
∠1 +∠4 = 180°
∠1 =∠2
∠1 =∠3
AB∥CD
思路1
思路2
思路1
推理:因为∠1 +∠4 = 180° (已知)
而∠2 +∠4 = 180 ° (邻补角的定义)
所以∠1 =∠2 (同角的补角相等)
所以AB∥CD
(同位角相等,两直线平行).
思路2
推理:因为∠1 +∠4 = 180° (已知)
而∠3 +∠4 = 180 °(邻补角的定义)
所以∠1 =∠3 (同角的补角相等)
所以AB∥CD
(内错角相等,两直线平行)
未知的新世界
已知的 (或已解决的) 问题
归纳
利用同旁内角,有判定两条直线平行的第三种方法:
判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
数学语言:
因为∠1 +∠4 = 180° (已知),
所以AB∥CD (同旁内角互补,两直线平行)
归纳
判定两条直线平行的三种方法:
判定方法1:同位角相等,两直线平行
判定方法2:内错角相等,两直线平行
判定方法3:同旁内角互补,两直线平行
角度的关系
直线的位置关系
例1 已知,如图,请分别依据所给出的条件,判定相应的哪两条直线平行?并写出推理的根据.
(1) 如果∠2 =∠5,那么 __________.
( __________ , __________ )
(2) 如果∠2 =∠3,那么 __________.
( __________ , __________ )
(3) 如果∠2 +∠1 = 180°,那么 __________.
( ______________ , __________ )
(4) 如果∠5 =∠3,那么 __________. ( __________ , __________ )
AB∥EF
同位角相等
两直线平行
EF∥DG
内错角相等
两直线平行
AD∥BC
同旁内角互补
两直线平行
AB∥CD
内错角相等
两直线平行
例2 在同一平面内,如果两条直线垂直于同一条直线,那么这两条直线平行吗?为什么?
a
b
c
分析:垂直总与直角联系在一起,进而用判断两条直线平行的方法进行判定.
答:这两条直线平行.理由如下:
如图,∵b⊥a,
∴∠1= 90°
同理∠2 = 90°
∴∠1= ∠2
∵∠1和 ∠2是同位角
∴b//c.(同位角相等,两直线平行)
符号“∵”表示“因为”,
符号“∴”表示“所以”.
你还能利用其他方法说明b//c吗?
1
2
a
b
c
1
2
a
b
c
答:这两条直线平行.理由如下:
如图,∵b⊥a,
∴∠1= 90°
同理∠2 = 90°
∴∠1= ∠2
∵∠1和 ∠2是内错角
∴b//c.(内错角相等,两直线平行)
1
2
a
b
c
答:这两条直线平行.理由如下:
如图,∵b⊥a,
∴∠1= 90°
同理∠2 = 90°
∴∠1= ∠2
∵∠1和 ∠2是同旁内角
∴b//c.(同旁内角互补,两直线平行)
1.如图所示,下列条件中,能判断 AB∥CD 的是 ( )
A. ∠BAD =∠BCD
B. ∠1 =∠2
C. ∠3 =∠4
D. ∠BAC =∠ACD
D
随堂练习
2.如图,已知∠2=110°,要使a∥b,则须具备的另一个条件是( )
A.∠3=70° B.∠3=110°
C.∠4=70° D.∠1=70°
A
3.如图,∠DAB+∠CDA=180°,∠ABC=∠1,直线AB与CD平行吗?直线AD与BC呢?为什么?
解:AB∥CD,AD∥BC.理由如下:
∵∠DAB+∠CDA=180°,
∴AB∥CD(同旁内角互补,两直线平行)
∵∠ABC=∠1,
∴AD∥BC(同位角相等,两直线平行).
判定方法1
平行线的
判定
同位角相等,两直线平行
判定方法2
同旁内角互补,两直线平行
内错角相等,两直线平行
板书设计
判定方法3
5.2.2 平行线的判定
1. 掌握平行线的三种判定方法;
2. 会用判定方法来判断两条直线是否平行.
学习目标
重点
难点
新课引入
根据平行线的定义,如果平面内的两条直线不相交,就可以判断这两条直线平行.但是,由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据定义来判断两条直线是否平行,那么,有没有其他判定方法呢?
新知学习
思考
我们以前已学习过用三角尺和直尺画平行线.在在这一过程中,三角尺起着怎样的作用?
C
D
简化上图画平行线的方法得到下图.可以看出,画直线AB的平行线CD,实际上就是画与∠2相等的∠1,而∠2和∠1正是直线AB,CD被直线EF截得的同位角.这说明,如果同位角相等,那么AB//CD.
归纳
一般地,有如下利用同位角判定两条直线平行的方法:
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
数学语言:
因为∠1 =∠2 (已知),
所以AB∥CD (内错角相等,两直线平行)
3
你能说出木工用图中的角尺画平行线的道理吗?
同位角相等,
两直线平行.
思考
如图,如果∠1 =∠3,能否得到 AB∥CD?
两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角.由同位角相等,可以判定两条直线平行,那么,能否利用内错角,或同旁内角来判定两条直线平行呢?
猜想:直线 AB,CD 被直线 EF 所截,如果∠1 =∠3,那么 AB∥CD.
推理:因为∠1 =∠3
而∠2 =∠3 (对顶角相等),
所以∠1 =∠2
所以AB∥CD (同位角相等,两直线平行).
归纳
由判定方法1,可以得出利用内错角判定两条直线平行的方法:
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
数学语言:
∵∠1 =∠3 (已知),
∴AB∥CD (内错角相等,两直线平行)
3
如图,∠1 和∠4 满足什么关系时,能得到 AB∥CD?
思考
猜想:直线 AB,CD 被直线 EF 所截,如果∠1 +∠4 = 180°,那么AB∥CD.
分析:
∠1 +∠4 = 180°
∠1 =∠2
∠1 =∠3
AB∥CD
思路1
思路2
思路1
推理:因为∠1 +∠4 = 180° (已知)
而∠2 +∠4 = 180 ° (邻补角的定义)
所以∠1 =∠2 (同角的补角相等)
所以AB∥CD
(同位角相等,两直线平行).
思路2
推理:因为∠1 +∠4 = 180° (已知)
而∠3 +∠4 = 180 °(邻补角的定义)
所以∠1 =∠3 (同角的补角相等)
所以AB∥CD
(内错角相等,两直线平行)
未知的新世界
已知的 (或已解决的) 问题
归纳
利用同旁内角,有判定两条直线平行的第三种方法:
判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
数学语言:
因为∠1 +∠4 = 180° (已知),
所以AB∥CD (同旁内角互补,两直线平行)
归纳
判定两条直线平行的三种方法:
判定方法1:同位角相等,两直线平行
判定方法2:内错角相等,两直线平行
判定方法3:同旁内角互补,两直线平行
角度的关系
直线的位置关系
例1 已知,如图,请分别依据所给出的条件,判定相应的哪两条直线平行?并写出推理的根据.
(1) 如果∠2 =∠5,那么 __________.
( __________ , __________ )
(2) 如果∠2 =∠3,那么 __________.
( __________ , __________ )
(3) 如果∠2 +∠1 = 180°,那么 __________.
( ______________ , __________ )
(4) 如果∠5 =∠3,那么 __________. ( __________ , __________ )
AB∥EF
同位角相等
两直线平行
EF∥DG
内错角相等
两直线平行
AD∥BC
同旁内角互补
两直线平行
AB∥CD
内错角相等
两直线平行
例2 在同一平面内,如果两条直线垂直于同一条直线,那么这两条直线平行吗?为什么?
a
b
c
分析:垂直总与直角联系在一起,进而用判断两条直线平行的方法进行判定.
答:这两条直线平行.理由如下:
如图,∵b⊥a,
∴∠1= 90°
同理∠2 = 90°
∴∠1= ∠2
∵∠1和 ∠2是同位角
∴b//c.(同位角相等,两直线平行)
符号“∵”表示“因为”,
符号“∴”表示“所以”.
你还能利用其他方法说明b//c吗?
1
2
a
b
c
1
2
a
b
c
答:这两条直线平行.理由如下:
如图,∵b⊥a,
∴∠1= 90°
同理∠2 = 90°
∴∠1= ∠2
∵∠1和 ∠2是内错角
∴b//c.(内错角相等,两直线平行)
1
2
a
b
c
答:这两条直线平行.理由如下:
如图,∵b⊥a,
∴∠1= 90°
同理∠2 = 90°
∴∠1= ∠2
∵∠1和 ∠2是同旁内角
∴b//c.(同旁内角互补,两直线平行)
1.如图所示,下列条件中,能判断 AB∥CD 的是 ( )
A. ∠BAD =∠BCD
B. ∠1 =∠2
C. ∠3 =∠4
D. ∠BAC =∠ACD
D
随堂练习
2.如图,已知∠2=110°,要使a∥b,则须具备的另一个条件是( )
A.∠3=70° B.∠3=110°
C.∠4=70° D.∠1=70°
A
3.如图,∠DAB+∠CDA=180°,∠ABC=∠1,直线AB与CD平行吗?直线AD与BC呢?为什么?
解:AB∥CD,AD∥BC.理由如下:
∵∠DAB+∠CDA=180°,
∴AB∥CD(同旁内角互补,两直线平行)
∵∠ABC=∠1,
∴AD∥BC(同位角相等,两直线平行).
判定方法1
平行线的
判定
同位角相等,两直线平行
判定方法2
同旁内角互补,两直线平行
内错角相等,两直线平行
板书设计
判定方法3
