人教版九年级数学下册第二十九章投影与视图检测题(含答案)
文档属性
| 名称 | 人教版九年级数学下册第二十九章投影与视图检测题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-28 14:14:20 | ||
图片预览

文档简介
第二十九章检测题
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.正方形在太阳光的投影下得到的几何图形一定是( )
A.正方形 B.平行四边形或一条线段
C.矩形 D.菱形
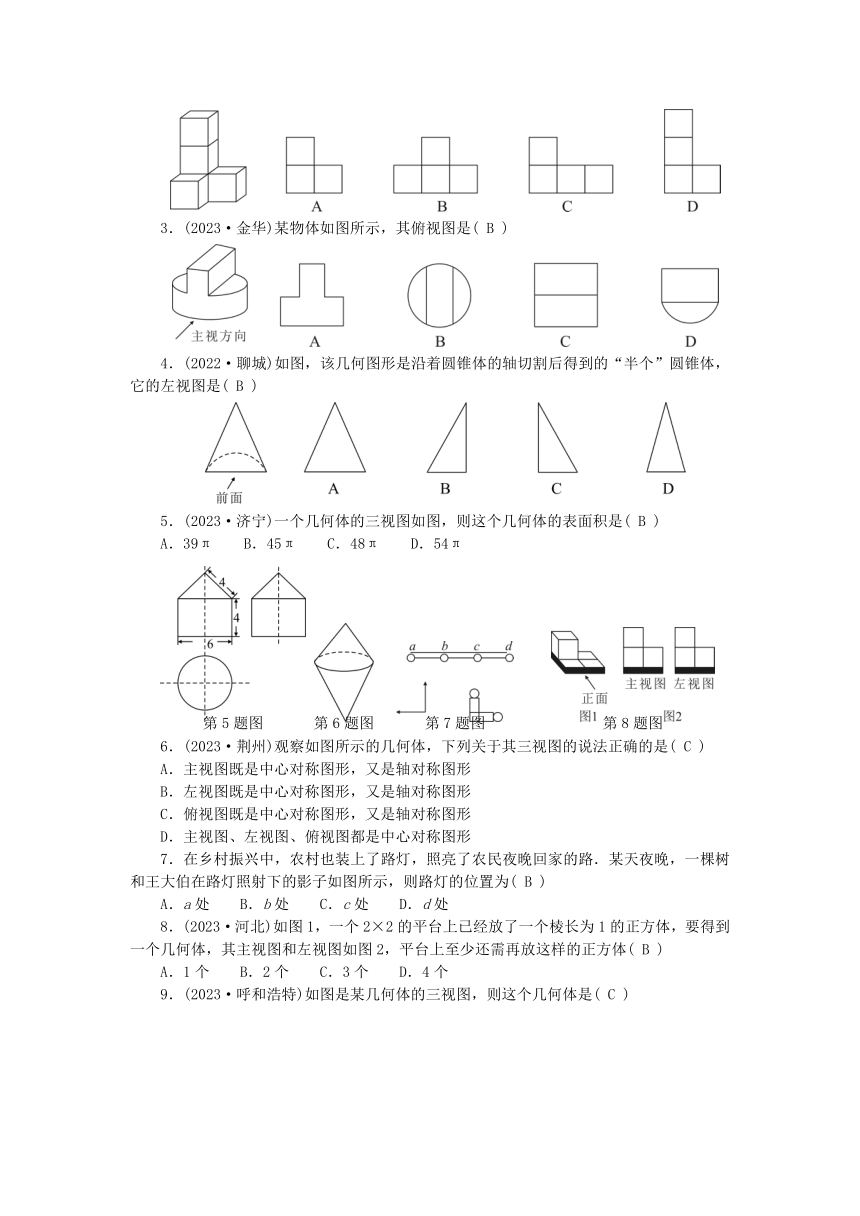
2.(2023·张家界)如图是由5个完全相同的小正方体组成的立体图形,其主视图是( )
3.(2023·金华)某物体如图所示,其俯视图是( )
4.(2022·聊城)如图,该几何图形是沿着圆锥体的轴切割后得到的“半个”圆锥体,它的左视图是( )
5.(2023·济宁)一个几何体的三视图如图,则这个几何体的表面积是( )
A.39π B.45π C.48π D.54π
6.(2023·荆州)观察如图所示的几何体,下列关于其三视图的说法正确的是( )
A.主视图既是中心对称图形,又是轴对称图形
B.左视图既是中心对称图形,又是轴对称图形
C.俯视图既是中心对称图形,又是轴对称图形
D.主视图、左视图、俯视图都是中心对称图形
7.在乡村振兴中,农村也装上了路灯,照亮了农民夜晚回家的路.某天夜晚,一棵树和王大伯在路灯照射下的影子如图所示,则路灯的位置为( )
A.a处 B.b处 C.c处 D.d处
8.(2023·河北)如图1,一个2×2的平台上已经放了一个棱长为1的正方体,要得到一个几何体,其主视图和左视图如图2,平台上至少还需再放这样的正方体( )
A.1个 B.2个 C.3个 D.4个
9.(2023·呼和浩特)如图是某几何体的三视图,则这个几何体是( )
10.如图,是一个由铁铸灌成的几何体的三视图,根据图中所标数据,铸灌这个几何体需要的铁的体积为( )
A.12π B.18π C.24π D.78π
二、填空题(每小题3分,共15分)
11.日晷是我国古代的一种计时仪器,它由晷面和晷针组成.当太阳光照在日晷上时,晷针的影子会随着时间的推移慢慢移动,以此来显示时刻,则晷针在晷面上形成的投影是__ __投影.(填“平行”或“中心”)
12.一个长方体的主视图和左视图如图所示(单位:cm),则其俯视图的面积是__ __.
13.小颖将几盒粉笔整齐地摞在讲台桌上,同学们发现从正面,左面,上面三个方向看到的粉笔形状相同(如图所示),那么这摞粉笔一共有__ __盒.
14.如图是一个正六棱柱的主视图和左视图,则图中a的值为__ __.
15.如图,一根直立于水平地面的木杆AB在灯光下形成影子AC(AC>AB),当木杆绕点A按逆时针方向旋转,直至到达地面时,影子的长度发生变化.已知AE=5 m,在旋转过程中,影长的最大值为5 m,最小值3 m,且影长最大时,木杆与光线垂直,则路灯EF的高度为__ __m.
三、解答题(共75分)
16.(8分)如图,若从正上方往下看第一排的四个物体,看到的是对应的四个平面图形,请分别用线把物体和平面图形对应连接起来.
17.(8分)画出如图所示几何体的三种视图.
18.(8分)已知:如图,AB和DE是直立在地面上的两根立柱,AB=5 m,某一时刻,AB在阳光下的投影BC=4 m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影长时,同时测出DE在阳光下的投影长为6 m,请你计算DE的长.
19.(9分)如图是一个几何体的三视图,根据所示数据,求该几何体的表面积和体积.
20.(10分)如图,一路灯距地面5.6米,身高1.6米的小方从距离灯的底部(点O)5米的A处,沿OA所在的直线行走到点C时,人影长度增长3米,求小方行走的路程.
21.(10分)如图是某几何体的三视图(俯视图是直角三角形).
(1)这个几何体是__ __;
(2)画出它的表面展开图;
(3)若主视图的宽为4 cm,长为8 cm,左视图的宽为3 cm,俯视图中斜边长为5 cm,求这个几何体中所有棱长的和、表面积.
22.(10分)根据要求完成下列题目:
(1)如图中有__8__块小正方体;
(2)请在下面方格纸中分别画出它的左视图和俯视图;
(3)用小正方体搭一个与(1)中不同的几何体,使得它的俯视图和左视图与你在方格中所画的图一致,则这样的几何体最少要__8__个小正方体,最多要__13__个小正方体.
23.(12分)如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.(取1.73)
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否晒到太阳?请说明理由.
第二十九章检测题
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.正方形在太阳光的投影下得到的几何图形一定是( B )
A.正方形 B.平行四边形或一条线段
C.矩形 D.菱形
2.(2023·张家界)如图是由5个完全相同的小正方体组成的立体图形,其主视图是( D )
3.(2023·金华)某物体如图所示,其俯视图是( B )
4.(2022·聊城)如图,该几何图形是沿着圆锥体的轴切割后得到的“半个”圆锥体,它的左视图是( B )
5.(2023·济宁)一个几何体的三视图如图,则这个几何体的表面积是( B )
A.39π B.45π C.48π D.54π
6.(2023·荆州)观察如图所示的几何体,下列关于其三视图的说法正确的是( C )
A.主视图既是中心对称图形,又是轴对称图形
B.左视图既是中心对称图形,又是轴对称图形
C.俯视图既是中心对称图形,又是轴对称图形
D.主视图、左视图、俯视图都是中心对称图形
7.在乡村振兴中,农村也装上了路灯,照亮了农民夜晚回家的路.某天夜晚,一棵树和王大伯在路灯照射下的影子如图所示,则路灯的位置为( B )
A.a处 B.b处 C.c处 D.d处
8.(2023·河北)如图1,一个2×2的平台上已经放了一个棱长为1的正方体,要得到一个几何体,其主视图和左视图如图2,平台上至少还需再放这样的正方体( B )
A.1个 B.2个 C.3个 D.4个
9.(2023·呼和浩特)如图是某几何体的三视图,则这个几何体是( C )
10.如图,是一个由铁铸灌成的几何体的三视图,根据图中所标数据,铸灌这个几何体需要的铁的体积为( B )
A.12π B.18π C.24π D.78π
二、填空题(每小题3分,共15分)
11.日晷是我国古代的一种计时仪器,它由晷面和晷针组成.当太阳光照在日晷上时,晷针的影子会随着时间的推移慢慢移动,以此来显示时刻,则晷针在晷面上形成的投影是__平行__投影.(填“平行”或“中心”)
12.一个长方体的主视图和左视图如图所示(单位:cm),则其俯视图的面积是__12_cm2__.
13.小颖将几盒粉笔整齐地摞在讲台桌上,同学们发现从正面,左面,上面三个方向看到的粉笔形状相同(如图所示),那么这摞粉笔一共有__4__盒.
14.如图是一个正六棱柱的主视图和左视图,则图中a的值为____.
15.如图,一根直立于水平地面的木杆AB在灯光下形成影子AC(AC>AB),当木杆绕点A按逆时针方向旋转,直至到达地面时,影子的长度发生变化.已知AE=5 m,在旋转过程中,影长的最大值为5 m,最小值3 m,且影长最大时,木杆与光线垂直,则路灯EF的高度为__7.5__m.
三、解答题(共75分)
16.(8分)如图,若从正上方往下看第一排的四个物体,看到的是对应的四个平面图形,请分别用线把物体和平面图形对应连接起来.
解:略
17.(8分)画出如图所示几何体的三种视图.
解:图形如图所示:
18.(8分)已知:如图,AB和DE是直立在地面上的两根立柱,AB=5 m,某一时刻,AB在阳光下的投影BC=4 m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影长时,同时测出DE在阳光下的投影长为6 m,请你计算DE的长.
解:(1)作法:连接AC,过点D作DF∥AC,交直线BE于F,如图所示,EF就是DE的投影 (2)∵太阳光线是平行的,∴AC∥DF.∴∠ACB=∠DFE.又∵∠ABC=∠DEF=90°,∴△ABC∽△DEF.∴=,∵AB=5 m,BC=4 m,EF=6 m,∴=,∴DE=7.5 m
19.(9分)如图是一个几何体的三视图,根据所示数据,求该几何体的表面积和体积.
解:该几何体的上面是底面直径为20 cm,高为32 cm的圆柱,下面是长为30 cm,宽为25 cm,高为40 cm的长方体,表面积为:30×25×2+30×40×2+25×40×2+π×20×32=(5900+640π) cm2,体积为:30×25×40+π×(20÷2)2×32=(30000+3200π) cm3
20.(10分)如图,一路灯距地面5.6米,身高1.6米的小方从距离灯的底部(点O)5米的A处,沿OA所在的直线行走到点C时,人影长度增长3米,求小方行走的路程.
解:∵AE⊥OD,GO⊥OD,∴EA∥GO,∴△AEB∽△OGB,∴=,∴=,解得AB=2米;∵OA所在的直线行走到点C时,人影长度增长3米,∴DC=5米,同理可得△DFC∽△DGO,∴=,即=,解得AC=7.5米.答:小方行走的路程AC为7.5米
21.(10分)如图是某几何体的三视图(俯视图是直角三角形).
(1)这个几何体是__三棱柱__;
(2)画出它的表面展开图;
(3)若主视图的宽为4 cm,长为8 cm,左视图的宽为3 cm,俯视图中斜边长为5 cm,求这个几何体中所有棱长的和、表面积.
解:(1)三棱柱
(2)它的表面展开图如图所示:
(3)这个几何体的所有棱长之和为:(3+4+5)×2+8×3=48(cm);它的表面积为:2××3×4+(3+4+5)×8=108(cm2).故这个几何体中所有棱长的和是48 cm,表面积是108 cm2
22.(10分)根据要求完成下列题目:
(1)如图中有__8__块小正方体;
(2)请在下面方格纸中分别画出它的左视图和俯视图;
(3)用小正方体搭一个与(1)中不同的几何体,使得它的俯视图和左视图与你在方格中所画的图一致,则这样的几何体最少要__8__个小正方体,最多要__13__个小正方体.
解:(1)由图可知,该几何体最下面一层有5个小正方体,第2层有2个小正方体,最上面一层有1个小正方体,∴共有5+2+1=8(块)小正方体.故答案为:8
(2)如图所示:
(3)这样的几何体所需正方体最少分布情况如图所示,共需要8个正方体;这样的几何体所需正方体最多分布情况如图所示,共需要正方体13个.故答案为:8;13
23.(12分)如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.(取1.73)
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否晒到太阳?请说明理由.
解:(1)当α=60°时,在Rt△ABE中,∵tan60°==,∴AB=10·tan60°=10≈10×1.73=17.3(米).即楼房的高度约为17.3米
(2)当α=45°时,小猫仍可以晒到太阳.理由如下:
假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为点F,与MC的交点为点H.∵∠BFA=45°,∴tan45°==1,此时的影长AF=AB=17.3米,∴CF=AF-AC=17.3-17.2=0.1米,∴CH=CF=0.1米,∴大楼的影子落在台阶MC这个侧面上,∴小猫能晒到太阳
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.正方形在太阳光的投影下得到的几何图形一定是( )
A.正方形 B.平行四边形或一条线段
C.矩形 D.菱形
2.(2023·张家界)如图是由5个完全相同的小正方体组成的立体图形,其主视图是( )
3.(2023·金华)某物体如图所示,其俯视图是( )
4.(2022·聊城)如图,该几何图形是沿着圆锥体的轴切割后得到的“半个”圆锥体,它的左视图是( )
5.(2023·济宁)一个几何体的三视图如图,则这个几何体的表面积是( )
A.39π B.45π C.48π D.54π
6.(2023·荆州)观察如图所示的几何体,下列关于其三视图的说法正确的是( )
A.主视图既是中心对称图形,又是轴对称图形
B.左视图既是中心对称图形,又是轴对称图形
C.俯视图既是中心对称图形,又是轴对称图形
D.主视图、左视图、俯视图都是中心对称图形
7.在乡村振兴中,农村也装上了路灯,照亮了农民夜晚回家的路.某天夜晚,一棵树和王大伯在路灯照射下的影子如图所示,则路灯的位置为( )
A.a处 B.b处 C.c处 D.d处
8.(2023·河北)如图1,一个2×2的平台上已经放了一个棱长为1的正方体,要得到一个几何体,其主视图和左视图如图2,平台上至少还需再放这样的正方体( )
A.1个 B.2个 C.3个 D.4个
9.(2023·呼和浩特)如图是某几何体的三视图,则这个几何体是( )
10.如图,是一个由铁铸灌成的几何体的三视图,根据图中所标数据,铸灌这个几何体需要的铁的体积为( )
A.12π B.18π C.24π D.78π
二、填空题(每小题3分,共15分)
11.日晷是我国古代的一种计时仪器,它由晷面和晷针组成.当太阳光照在日晷上时,晷针的影子会随着时间的推移慢慢移动,以此来显示时刻,则晷针在晷面上形成的投影是__ __投影.(填“平行”或“中心”)
12.一个长方体的主视图和左视图如图所示(单位:cm),则其俯视图的面积是__ __.
13.小颖将几盒粉笔整齐地摞在讲台桌上,同学们发现从正面,左面,上面三个方向看到的粉笔形状相同(如图所示),那么这摞粉笔一共有__ __盒.
14.如图是一个正六棱柱的主视图和左视图,则图中a的值为__ __.
15.如图,一根直立于水平地面的木杆AB在灯光下形成影子AC(AC>AB),当木杆绕点A按逆时针方向旋转,直至到达地面时,影子的长度发生变化.已知AE=5 m,在旋转过程中,影长的最大值为5 m,最小值3 m,且影长最大时,木杆与光线垂直,则路灯EF的高度为__ __m.
三、解答题(共75分)
16.(8分)如图,若从正上方往下看第一排的四个物体,看到的是对应的四个平面图形,请分别用线把物体和平面图形对应连接起来.
17.(8分)画出如图所示几何体的三种视图.
18.(8分)已知:如图,AB和DE是直立在地面上的两根立柱,AB=5 m,某一时刻,AB在阳光下的投影BC=4 m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影长时,同时测出DE在阳光下的投影长为6 m,请你计算DE的长.
19.(9分)如图是一个几何体的三视图,根据所示数据,求该几何体的表面积和体积.
20.(10分)如图,一路灯距地面5.6米,身高1.6米的小方从距离灯的底部(点O)5米的A处,沿OA所在的直线行走到点C时,人影长度增长3米,求小方行走的路程.
21.(10分)如图是某几何体的三视图(俯视图是直角三角形).
(1)这个几何体是__ __;
(2)画出它的表面展开图;
(3)若主视图的宽为4 cm,长为8 cm,左视图的宽为3 cm,俯视图中斜边长为5 cm,求这个几何体中所有棱长的和、表面积.
22.(10分)根据要求完成下列题目:
(1)如图中有__8__块小正方体;
(2)请在下面方格纸中分别画出它的左视图和俯视图;
(3)用小正方体搭一个与(1)中不同的几何体,使得它的俯视图和左视图与你在方格中所画的图一致,则这样的几何体最少要__8__个小正方体,最多要__13__个小正方体.
23.(12分)如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.(取1.73)
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否晒到太阳?请说明理由.
第二十九章检测题
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.正方形在太阳光的投影下得到的几何图形一定是( B )
A.正方形 B.平行四边形或一条线段
C.矩形 D.菱形
2.(2023·张家界)如图是由5个完全相同的小正方体组成的立体图形,其主视图是( D )
3.(2023·金华)某物体如图所示,其俯视图是( B )
4.(2022·聊城)如图,该几何图形是沿着圆锥体的轴切割后得到的“半个”圆锥体,它的左视图是( B )
5.(2023·济宁)一个几何体的三视图如图,则这个几何体的表面积是( B )
A.39π B.45π C.48π D.54π
6.(2023·荆州)观察如图所示的几何体,下列关于其三视图的说法正确的是( C )
A.主视图既是中心对称图形,又是轴对称图形
B.左视图既是中心对称图形,又是轴对称图形
C.俯视图既是中心对称图形,又是轴对称图形
D.主视图、左视图、俯视图都是中心对称图形
7.在乡村振兴中,农村也装上了路灯,照亮了农民夜晚回家的路.某天夜晚,一棵树和王大伯在路灯照射下的影子如图所示,则路灯的位置为( B )
A.a处 B.b处 C.c处 D.d处
8.(2023·河北)如图1,一个2×2的平台上已经放了一个棱长为1的正方体,要得到一个几何体,其主视图和左视图如图2,平台上至少还需再放这样的正方体( B )
A.1个 B.2个 C.3个 D.4个
9.(2023·呼和浩特)如图是某几何体的三视图,则这个几何体是( C )
10.如图,是一个由铁铸灌成的几何体的三视图,根据图中所标数据,铸灌这个几何体需要的铁的体积为( B )
A.12π B.18π C.24π D.78π
二、填空题(每小题3分,共15分)
11.日晷是我国古代的一种计时仪器,它由晷面和晷针组成.当太阳光照在日晷上时,晷针的影子会随着时间的推移慢慢移动,以此来显示时刻,则晷针在晷面上形成的投影是__平行__投影.(填“平行”或“中心”)
12.一个长方体的主视图和左视图如图所示(单位:cm),则其俯视图的面积是__12_cm2__.
13.小颖将几盒粉笔整齐地摞在讲台桌上,同学们发现从正面,左面,上面三个方向看到的粉笔形状相同(如图所示),那么这摞粉笔一共有__4__盒.
14.如图是一个正六棱柱的主视图和左视图,则图中a的值为____.
15.如图,一根直立于水平地面的木杆AB在灯光下形成影子AC(AC>AB),当木杆绕点A按逆时针方向旋转,直至到达地面时,影子的长度发生变化.已知AE=5 m,在旋转过程中,影长的最大值为5 m,最小值3 m,且影长最大时,木杆与光线垂直,则路灯EF的高度为__7.5__m.
三、解答题(共75分)
16.(8分)如图,若从正上方往下看第一排的四个物体,看到的是对应的四个平面图形,请分别用线把物体和平面图形对应连接起来.
解:略
17.(8分)画出如图所示几何体的三种视图.
解:图形如图所示:
18.(8分)已知:如图,AB和DE是直立在地面上的两根立柱,AB=5 m,某一时刻,AB在阳光下的投影BC=4 m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影长时,同时测出DE在阳光下的投影长为6 m,请你计算DE的长.
解:(1)作法:连接AC,过点D作DF∥AC,交直线BE于F,如图所示,EF就是DE的投影 (2)∵太阳光线是平行的,∴AC∥DF.∴∠ACB=∠DFE.又∵∠ABC=∠DEF=90°,∴△ABC∽△DEF.∴=,∵AB=5 m,BC=4 m,EF=6 m,∴=,∴DE=7.5 m
19.(9分)如图是一个几何体的三视图,根据所示数据,求该几何体的表面积和体积.
解:该几何体的上面是底面直径为20 cm,高为32 cm的圆柱,下面是长为30 cm,宽为25 cm,高为40 cm的长方体,表面积为:30×25×2+30×40×2+25×40×2+π×20×32=(5900+640π) cm2,体积为:30×25×40+π×(20÷2)2×32=(30000+3200π) cm3
20.(10分)如图,一路灯距地面5.6米,身高1.6米的小方从距离灯的底部(点O)5米的A处,沿OA所在的直线行走到点C时,人影长度增长3米,求小方行走的路程.
解:∵AE⊥OD,GO⊥OD,∴EA∥GO,∴△AEB∽△OGB,∴=,∴=,解得AB=2米;∵OA所在的直线行走到点C时,人影长度增长3米,∴DC=5米,同理可得△DFC∽△DGO,∴=,即=,解得AC=7.5米.答:小方行走的路程AC为7.5米
21.(10分)如图是某几何体的三视图(俯视图是直角三角形).
(1)这个几何体是__三棱柱__;
(2)画出它的表面展开图;
(3)若主视图的宽为4 cm,长为8 cm,左视图的宽为3 cm,俯视图中斜边长为5 cm,求这个几何体中所有棱长的和、表面积.
解:(1)三棱柱
(2)它的表面展开图如图所示:
(3)这个几何体的所有棱长之和为:(3+4+5)×2+8×3=48(cm);它的表面积为:2××3×4+(3+4+5)×8=108(cm2).故这个几何体中所有棱长的和是48 cm,表面积是108 cm2
22.(10分)根据要求完成下列题目:
(1)如图中有__8__块小正方体;
(2)请在下面方格纸中分别画出它的左视图和俯视图;
(3)用小正方体搭一个与(1)中不同的几何体,使得它的俯视图和左视图与你在方格中所画的图一致,则这样的几何体最少要__8__个小正方体,最多要__13__个小正方体.
解:(1)由图可知,该几何体最下面一层有5个小正方体,第2层有2个小正方体,最上面一层有1个小正方体,∴共有5+2+1=8(块)小正方体.故答案为:8
(2)如图所示:
(3)这样的几何体所需正方体最少分布情况如图所示,共需要8个正方体;这样的几何体所需正方体最多分布情况如图所示,共需要正方体13个.故答案为:8;13
23.(12分)如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.(取1.73)
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否晒到太阳?请说明理由.
解:(1)当α=60°时,在Rt△ABE中,∵tan60°==,∴AB=10·tan60°=10≈10×1.73=17.3(米).即楼房的高度约为17.3米
(2)当α=45°时,小猫仍可以晒到太阳.理由如下:
假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为点F,与MC的交点为点H.∵∠BFA=45°,∴tan45°==1,此时的影长AF=AB=17.3米,∴CF=AF-AC=17.3-17.2=0.1米,∴CH=CF=0.1米,∴大楼的影子落在台阶MC这个侧面上,∴小猫能晒到太阳
