球的外接、内切问题 -2024届高三数学二轮专题复习 课件(共30张PPT)
文档属性
| 名称 | 球的外接、内切问题 -2024届高三数学二轮专题复习 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-26 18:27:06 | ||
图片预览




文档简介
(共30张PPT)
专题:与球有关的内切与外接问题二、球与多面体的接、切
定义1:若一个多面体的各顶点都在一个球的球面上,
则称这个多面体是这个球的内接多面体,
这个球是这个 。
定义2:若一个多面体的各面都与一个球的球面相切,
则称这个多面体是这个球的外切多面体,
这个球是这个 。
一、
球体的体积与表面积
①
②
多面体的外接球
多面体的内切球
棱切:
一个几何体各个面分别与另一个几何体各条棱相切。
图3
图4
图5
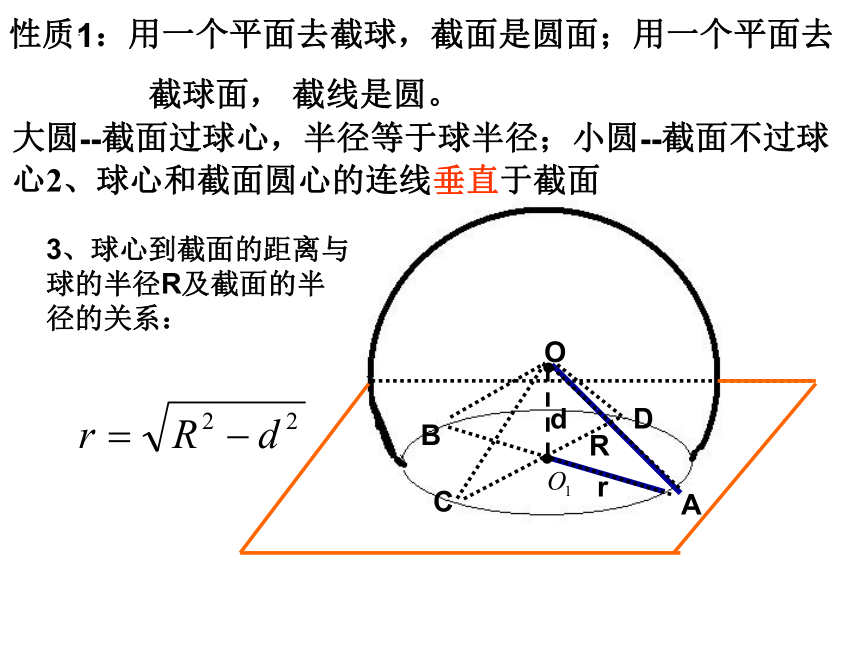
2、球心和截面圆心的连线垂直于截面
O
A
B
C
D
d
r
R
3、球心到截面的距离与球的半径R及截面的半径的关系:
性质1:用一个平面去截球,截面是圆面;用一个平面去
截球面, 截线是圆。
大圆--截面过球心,半径等于球半径;小圆--截面不过球心
有关多面体外接球的问题,是立体几何的一个重点,也是高考考查的一个热点.研究多面体的外接球问题,既要运用多面体的知识,又要运用球的知识,并且还要特别注意多面体的有关几何元素与球的半径之间的关系,而多面体外接球半径的求法在解题中往往会起到至关重要的作用.
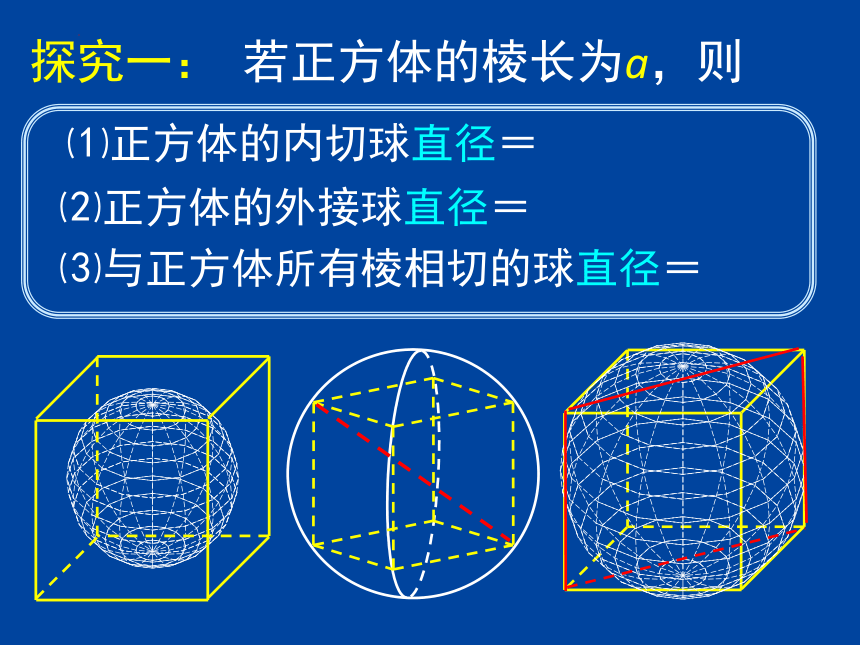
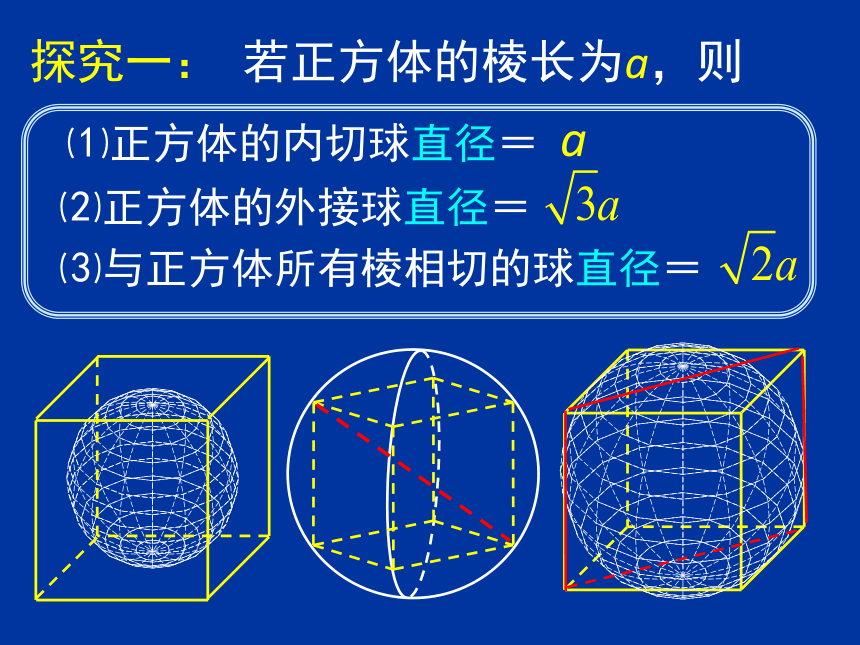
⑴正方体的内切球直径=
⑵正方体的外接球直径=
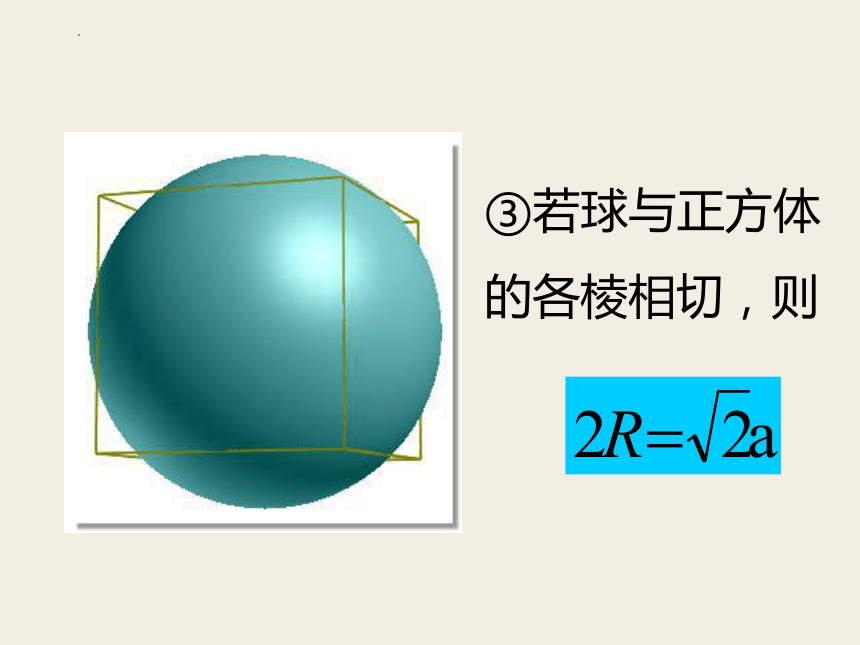
⑶与正方体所有棱相切的球直径=
探究一: 若正方体的棱长为a,则
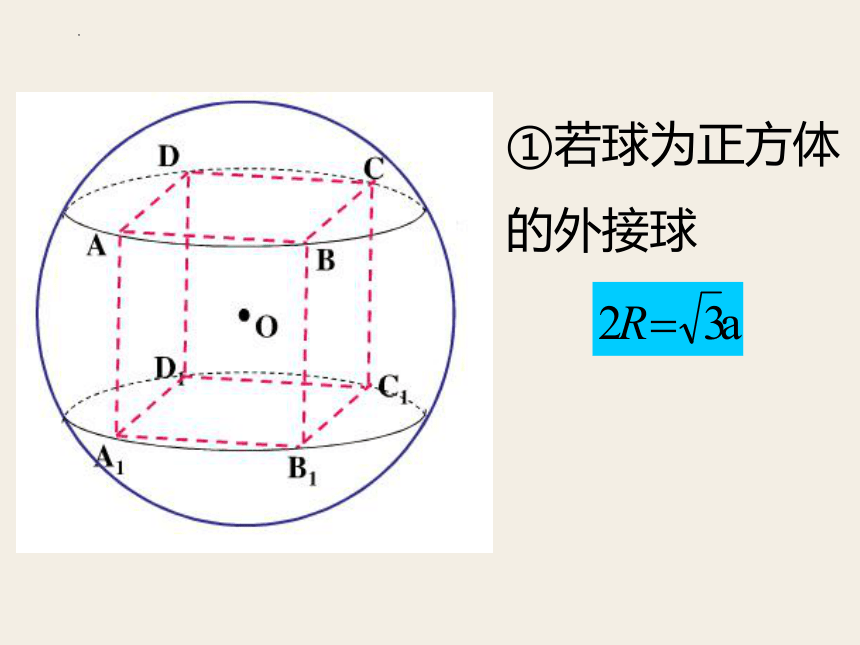
①若球为正方体
的外接球
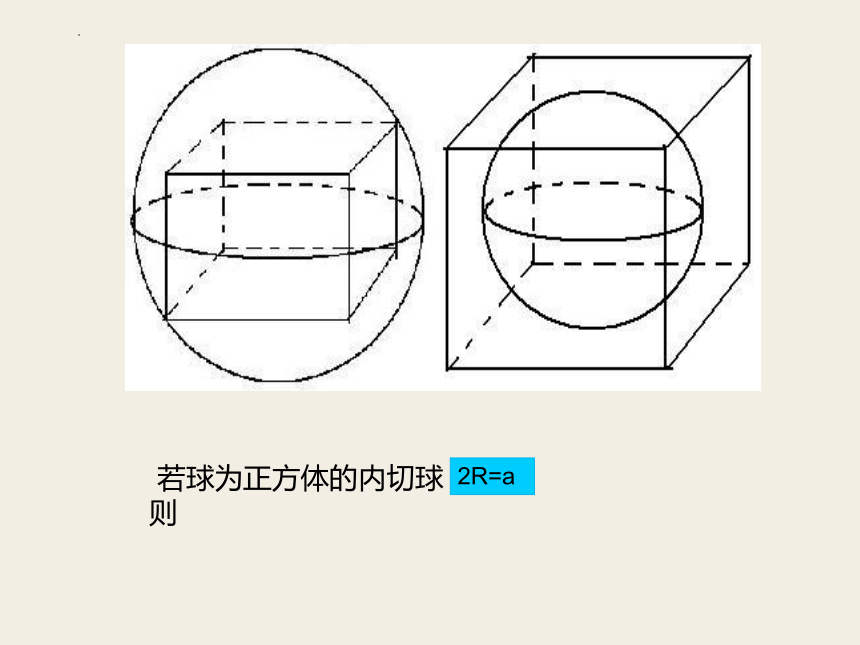
若球为正方体的内切球,则
2R=a
③若球与正方体的各棱相切,则
⑴正方体的内切球直径=
⑵正方体的外接球直径=
⑶与正方体所有棱相切的球直径=
探究一: 若正方体的棱长为a,则
a
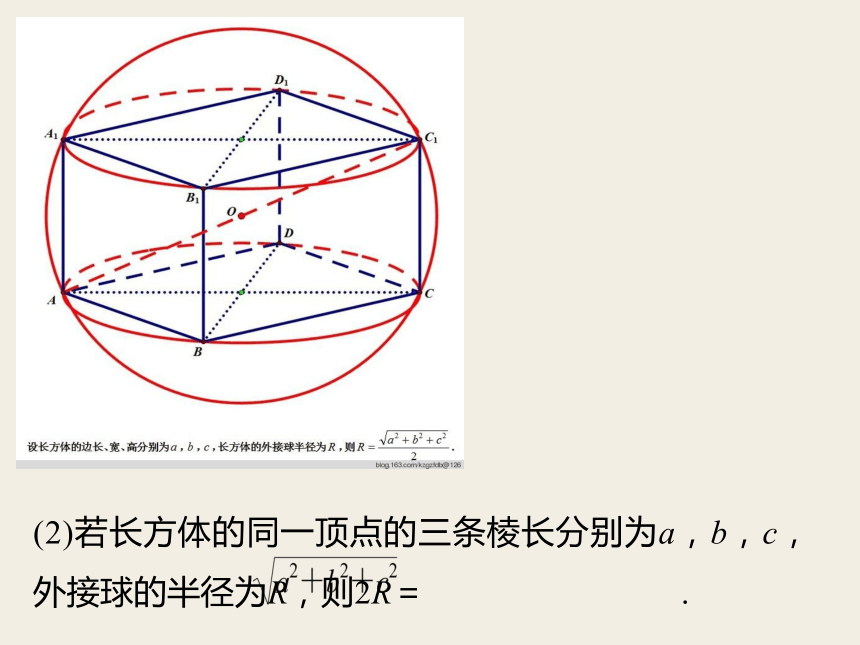
(2)若长方体的同一顶点的三条棱长分别为a,b,c,外接球的半径为R,则2R= .
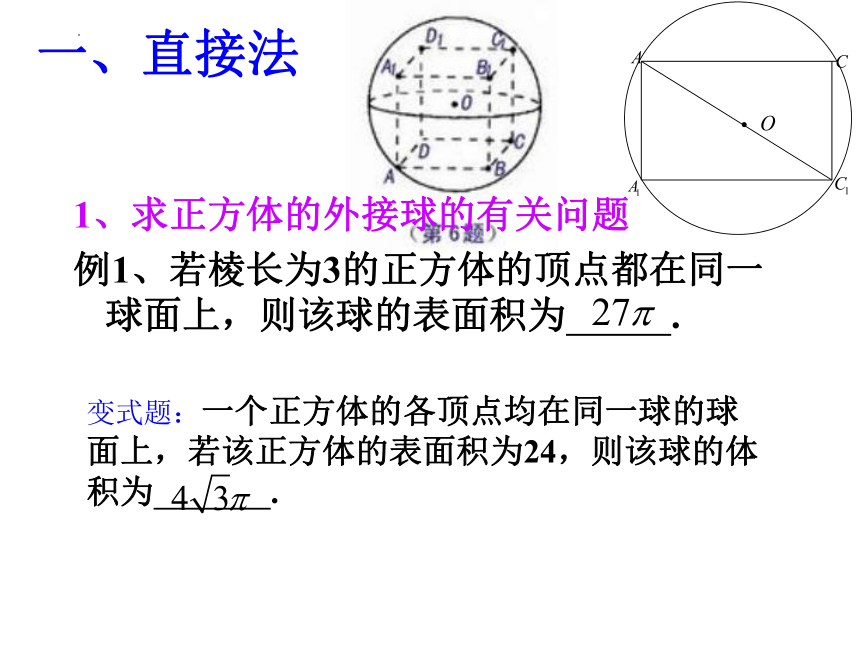
一、直接法
变式题:一个正方体的各顶点均在同一球的球面上,若该正方体的表面积为24,则该球的体积为 .
1、求正方体的外接球的有关问题
例1、若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为 .
2、求长方体的外接球的有关问题
例2、一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱长分别为1,2,3 ,则此球的表面积为 .
解析:关键是求出球的半径,因为长方体内接于球,所以它的体对角线正好为球的直径。长方体体对角线长为 ,故球的表面积为 .
变式题:已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积为( )
A. B. C. D.
C
中截面
设棱长为1
球的外切正方体的棱长等于球直径。
A
B
C
D
D1
C1
B1
A1
O
例1 甲球内切于正方体的各面,乙球内切于该正方体的各条棱,
丙球外接于该正方体,则三球表面面积之比为( )
A. 1:2:3 B. C. D.
球与棱柱的组合体问题
A
B
C
D
D1
C1
B1
A1
O
中截面
正方形的对角线等于球的直径。
.
球内切于正方体的棱
设棱长为1
A
B
C
D
D1
C1
A1
O
B1
对角面
球的内接正方体的对角线等于球直径。
球外接于正方体
设棱长为1
1. 已知长方体的长、宽、高分别是 、 、1 ,求长方体的外接球的体积。变题:2. 已知球O的表面上有P、A、B、C四点,且PA、PB、PC两两互相垂直,若PA=3,PB=4,PC=5,求这个球的表面积和体积。沿对角面截得:ACBPO半球的半径为R,一正方体的四个顶点在半球的底面上,另四个顶点在球面上,求正方体的棱长球与正四面体的切与接
⑴正四面体的内切球直径=
⑵正四面体的外接球直径=
⑶与正四面体所有棱相切的球直=
探究二: 若正四面体的棱长为a,则
求棱长为a的正四面体外接球、内切球及棱切球的半径.
[解] 设正四面体A—BCD的高为AO1,外接
球球心为O,半径为R,如图所示.
A
B
C
D
O
A
B
C
D
O
求正四面体外接球的半径
求正方体外接球的半径
解法2:
典型:正四面体ABCD的棱长为a,求其内切球半径r与外接球半径R.
思考:若正四面体变成正三棱锥,方法是否有变化?
1、内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等
2、正多面体的内切球和外接球的球心重合
3、正棱锥的内切球和外接球球心都在高线上,但不重合
4、基本方法:构造三角形利用相似比和勾股定理
5、体积分割是求内切球半径的通用做法
1.正方体的内切球、棱切球、外接球
设正方体的棱长为a,则: 正方体的内切球、外接球、棱切球直径
径分别为:
2.正四面体的内切球、棱切球、外接球
设正四面体的棱长为a,则: 正四面体的内切球、棱切球、外接球
半径分别为:
圆锥的内切球
圆锥的外接球
圆锥内接正四棱柱
结论:
1.正方体的外接球的球心是体对角线的交点,半径是体对角线的一半
2.正方体的内切球的球心是体对角线的交点,半径是棱长的一半
3.与正方体的棱都相切的球的球心是体对角线的交点,半径是面对角线长的一半
A
B
C
D
D1
C1
B1
A1
O
球内接正方体
球外切正方体(切面)
球外切正方体(切棱)
思维升华
空间几何体与球接、切问题的求解方法
(1)求解球与棱柱、棱锥的接、切问题时,一般过球心及接、切点作截面,把空间问题转化为平面图形与圆的接、切问题,再利用平面几何知识寻找几何中元素间的关系求解.
(2)若球面上四点P,A,B,C构成的三条线段PA,PB,PC两两互相垂直,且PA=a,PB=b,PC=c,一般把有关元素“补形”成为一个球内接长方体,利用4R2=a2+b2+c2求解.
课时小结:解决与球有关的内切与外接问题的关键是:通过寻找恰当的过球心的截面,把立体问题转化为平面问题,通过解三角形求出球的半径R.
专题:与球有关的内切与外接问题二、球与多面体的接、切
定义1:若一个多面体的各顶点都在一个球的球面上,
则称这个多面体是这个球的内接多面体,
这个球是这个 。
定义2:若一个多面体的各面都与一个球的球面相切,
则称这个多面体是这个球的外切多面体,
这个球是这个 。
一、
球体的体积与表面积
①
②
多面体的外接球
多面体的内切球
棱切:
一个几何体各个面分别与另一个几何体各条棱相切。
图3
图4
图5
2、球心和截面圆心的连线垂直于截面
O
A
B
C
D
d
r
R
3、球心到截面的距离与球的半径R及截面的半径的关系:
性质1:用一个平面去截球,截面是圆面;用一个平面去
截球面, 截线是圆。
大圆--截面过球心,半径等于球半径;小圆--截面不过球心
有关多面体外接球的问题,是立体几何的一个重点,也是高考考查的一个热点.研究多面体的外接球问题,既要运用多面体的知识,又要运用球的知识,并且还要特别注意多面体的有关几何元素与球的半径之间的关系,而多面体外接球半径的求法在解题中往往会起到至关重要的作用.
⑴正方体的内切球直径=
⑵正方体的外接球直径=
⑶与正方体所有棱相切的球直径=
探究一: 若正方体的棱长为a,则
①若球为正方体
的外接球
若球为正方体的内切球,则
2R=a
③若球与正方体的各棱相切,则
⑴正方体的内切球直径=
⑵正方体的外接球直径=
⑶与正方体所有棱相切的球直径=
探究一: 若正方体的棱长为a,则
a
(2)若长方体的同一顶点的三条棱长分别为a,b,c,外接球的半径为R,则2R= .
一、直接法
变式题:一个正方体的各顶点均在同一球的球面上,若该正方体的表面积为24,则该球的体积为 .
1、求正方体的外接球的有关问题
例1、若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为 .
2、求长方体的外接球的有关问题
例2、一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱长分别为1,2,3 ,则此球的表面积为 .
解析:关键是求出球的半径,因为长方体内接于球,所以它的体对角线正好为球的直径。长方体体对角线长为 ,故球的表面积为 .
变式题:已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积为( )
A. B. C. D.
C
中截面
设棱长为1
球的外切正方体的棱长等于球直径。
A
B
C
D
D1
C1
B1
A1
O
例1 甲球内切于正方体的各面,乙球内切于该正方体的各条棱,
丙球外接于该正方体,则三球表面面积之比为( )
A. 1:2:3 B. C. D.
球与棱柱的组合体问题
A
B
C
D
D1
C1
B1
A1
O
中截面
正方形的对角线等于球的直径。
.
球内切于正方体的棱
设棱长为1
A
B
C
D
D1
C1
A1
O
B1
对角面
球的内接正方体的对角线等于球直径。
球外接于正方体
设棱长为1
1. 已知长方体的长、宽、高分别是 、 、1 ,求长方体的外接球的体积。变题:2. 已知球O的表面上有P、A、B、C四点,且PA、PB、PC两两互相垂直,若PA=3,PB=4,PC=5,求这个球的表面积和体积。沿对角面截得:ACBPO半球的半径为R,一正方体的四个顶点在半球的底面上,另四个顶点在球面上,求正方体的棱长球与正四面体的切与接
⑴正四面体的内切球直径=
⑵正四面体的外接球直径=
⑶与正四面体所有棱相切的球直=
探究二: 若正四面体的棱长为a,则
求棱长为a的正四面体外接球、内切球及棱切球的半径.
[解] 设正四面体A—BCD的高为AO1,外接
球球心为O,半径为R,如图所示.
A
B
C
D
O
A
B
C
D
O
求正四面体外接球的半径
求正方体外接球的半径
解法2:
典型:正四面体ABCD的棱长为a,求其内切球半径r与外接球半径R.
思考:若正四面体变成正三棱锥,方法是否有变化?
1、内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等
2、正多面体的内切球和外接球的球心重合
3、正棱锥的内切球和外接球球心都在高线上,但不重合
4、基本方法:构造三角形利用相似比和勾股定理
5、体积分割是求内切球半径的通用做法
1.正方体的内切球、棱切球、外接球
设正方体的棱长为a,则: 正方体的内切球、外接球、棱切球直径
径分别为:
2.正四面体的内切球、棱切球、外接球
设正四面体的棱长为a,则: 正四面体的内切球、棱切球、外接球
半径分别为:
圆锥的内切球
圆锥的外接球
圆锥内接正四棱柱
结论:
1.正方体的外接球的球心是体对角线的交点,半径是体对角线的一半
2.正方体的内切球的球心是体对角线的交点,半径是棱长的一半
3.与正方体的棱都相切的球的球心是体对角线的交点,半径是面对角线长的一半
A
B
C
D
D1
C1
B1
A1
O
球内接正方体
球外切正方体(切面)
球外切正方体(切棱)
思维升华
空间几何体与球接、切问题的求解方法
(1)求解球与棱柱、棱锥的接、切问题时,一般过球心及接、切点作截面,把空间问题转化为平面图形与圆的接、切问题,再利用平面几何知识寻找几何中元素间的关系求解.
(2)若球面上四点P,A,B,C构成的三条线段PA,PB,PC两两互相垂直,且PA=a,PB=b,PC=c,一般把有关元素“补形”成为一个球内接长方体,利用4R2=a2+b2+c2求解.
课时小结:解决与球有关的内切与外接问题的关键是:通过寻找恰当的过球心的截面,把立体问题转化为平面问题,通过解三角形求出球的半径R.
同课章节目录
