河南省南阳市部分中学2023-2024学年高一上学期期末联考数学试题(含答案)
文档属性
| 名称 | 河南省南阳市部分中学2023-2024学年高一上学期期末联考数学试题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 786.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-26 00:00:00 | ||
图片预览





文档简介
南阳市部分中学2023-2024学年高一上学期期末联考
数学试题
一、单选题
1.已知,,若集合,则的值为( )
A. B. C.1 D.2
2.已知点在幂函数的图象上,设,,,则a,b,c的大小关系为( )
A. B. C. D.
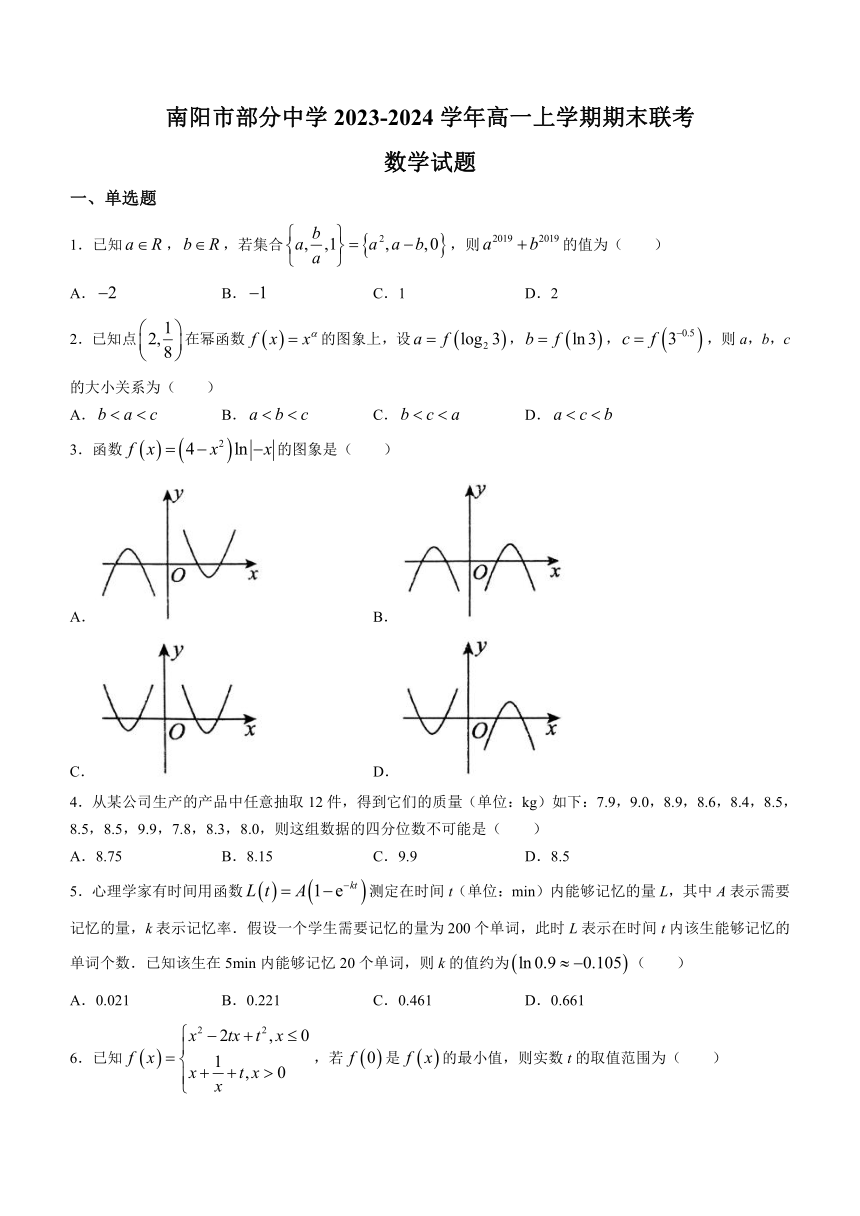
3.函数的图象是( )
A. B.
C. D.
4.从某公司生产的产品中任意抽取12件,得到它们的质量(单位:kg)如下:7.9,9.0,8.9,8.6,8.4,8.5,8.5,8.5,9.9,7.8,8.3,8.0,则这组数据的四分位数不可能是( )
A.8.75 B.8.15 C.9.9 D.8.5
5.心理学家有时间用函数测定在时间t(单位:min)内能够记忆的量L,其中A表示需要记忆的量,k表示记忆率.假设一个学生需要记忆的量为200个单词,此时L表示在时间t内该生能够记忆的单词个数.已知该生在5min内能够记忆20个单词,则k的值约为( )
A.0.021 B.0.221 C.0.461 D.0.661
6.已知,若是的最小值,则实数t的取值范围为( )
A. B. C. D.
7.已知函数,正实数a,b满足,则的最大值为( )
A. B. C. D.
8.已知函数既是二次函数又是幂函数,若函数,则( )
A.2023 B.2024 C.4046 D.4047
二、多选题
9.下列说法中正确的有( )
A.命题,,则命题p的否定是,
B.“”是“”的必要条件
C.若命题“,”是真命题,则a的取值范围为
D.“”是“关于x的方程有一正一负根”的充要条件
10.已知一组样本数据,现有一组新的,则与原样本数据相比,新的样本数据( )
A.平均数不变 B.中位数不变 C.极差变小 D.方差变小
11.若函数在上满足:对任意的,当时,恒有,则称函数为“理想函数”.下列函数能被称为“理想函数”的有( )
A. B.
C. D.
12.数学上,高斯符号(Gauss mark)是指对取整符号和取小符号的统称,用于数论等领域.定义在数学特别是数论领域中,有时需要略去一个实数的小数部分只研究它的整数部分,或需要略去整数部分研究小数部分,因而引入高斯符号.设,用表示不超过x的最大整数.比如:,,,,…,已知函数,则下列说法不正确的是( )
A.的值域为 B.在为减函数
C.方程无实根 D.方程仅有一个实根
三、填空题
13.某校教师男女人数之比为,该校所有教师进行1分钟限时投篮比赛.现记录了每个教师1分钟命中次数,已知男教师命中次数的平均数为17,方差为16,女教师命中次数的平均数为8,方差为16,那么全体教师1分钟限时投篮次数的方差为______.
14.已知函数在上有一个零点,用二分法求零点的近似值(精确度为0.1)时,至少需要进行______次中点函数值的计算.
15.已知函数在上单调递增,则实数a的取值范围是______.
16设函数,给出下列四个结论:
①对,方程都有3个实数根;
②,使得;
③若互不相等的实数满足,则的取值范围是.
其中所有正确结论的序号是______.
四、解答题
17.(1)计算
(2)计算.
18,函数的定义域为集合A,集合,.
(1)求集合A,B;
(2)设,,且p是q的必要不充分条件,求实数m的取值范围.
19.抛掷一枚均匀的骰子2次,将第1次掷出的点数记为a,第2次掷出的点数记为b.
(1)求的概率;
(2)记事件A为“”,事件B为“”,若且事件A和事件B为相互独立事件,求m的值.
20.设D是函数定义域的一个子集,若存在,使得成立,则称是的一个“准不动点”,也称在区间D上存在准不动点.已知.
(1)若,求函数的准不动点;
(2)若函数在区间上存在准不动点,求实数a的取值范围.
21.第19届亚运会将于2023年9月23日至10月8日在杭州举行,而亚运会志愿者的服务工作是举办一届成功的亚运会的重要保障.为配合亚运会志愿者选拔,某高校举行了志愿者选拔面试,面试成绩满分100分,现随机抽取了80名候选者的面试成绩,绘制成如下频率分布直方图.
(1)求a的值,并估计这80名候选者面试成绩平均值,众数,中位数;(同一组中的数据用该组区间的中点值作代表,中位数精确到0.1)
(2)乒乓球项目场地志愿服务需要3名志愿者,有3名男生和2名女生通过该项志愿服务选拔,需要通过抽签的方式决定最终的人选,现将3张写有“中签”和2张写有“未中签”字样的字条随机分配给每一位候选人,求中签者中男生比女生多的概率.
22.设,函数.
(1)若,求证:函数为奇函数;
(2)若,判断并证明函数的单调性;
(3)若,函数在区间上的取值范围是,求的范围.
南阳市部分中学2023-2024学年高一上学期期末联考
数学答案
1.B 2.B 3.B 4.C 5.A 6.C 7.B
8.D 【详解】函数既是二次函数又是幂函数,∴,∴为偶函数;
因为函数是R上的奇函数,
所以为定义域R上的奇函数;
,
.故选:D.
9.ACD
10.ACD 【详解】对于A,新数据的总和为:,与原数据总和相等,且数据个数都是n,因此平均数不变,A正确;
对于B,不妨设原数据为:1,2.5,3,中位数为2.5,则新数据为:1.75,2.75,2,中位数为2,B错误;
对于C,原数据极差为:,新数据极差为:,
而,即极差变小了,C正确;
对于D,由于两组数据的平均数不变,而极差变小,说明新数据相对原数据更集中于平均数,因此方差变小,D正确.故选:ACD.
11.ABD 【详解】不妨设,则由题意可得,即,由单调性定义可知,函数在上单调递增,即若在上单调递增,则称函数为“理想函数”.
A选项中,该函数在上单调递增,符合“理想函数”的定义;
B选项中,该函数在上单调递增,符合“理想函数”的定义;
C选项中,该函数在上单调递减,不符合“理想函数”的定义;
D选项中.该函数在上单调递增,符合“理想函数”的定义.
故选:ABD.
12.AB 【详解】由高斯函数的定义可得:当时,,则,
当时,,则,当时,,则,
当时,,则,当时,,则,
绘制函数图象如图所示,
对于A,由图可知,在上的值域为,不正确;
对于B,当时,的每段函数都是单调递减,但是在不是减函数,不正确;
对于C,由选项A知,在上的值域为,
所以方程无实根,正确:
对于D,当时,即,解得,
当时,即,解得,
结合函数图象知,方程仅有一个实根,正确.
故选:AB.
13.36 14.4 15.
16.②③
【详解】当时,的图象是开口向上、对称轴为直线的抛物线在y轴及左侧部分,
当时,的图象是对数函数的图象向上平移1个单位而得,如图,
对于①,观察图象知,当时,方程只有2个实数根,①错误;
对于②,当时,使得有成立,即与有交点,
而的图象与函数的图象关于y轴对称,
显然的图象与函数的图象有公共点,②正确;
对于③,不妨设互不相等的实数且,当满足时,
由图可知,即,当,,即时,,
当,,即时,,因此,
所以,③正确,
所以所有正确结论的序号是②③.
故答案为:②③
17.(1)0;(2)3
【详解】(1)
.
(2)
.
18.(1),;
(2)
【分析】(1)根据定义域列一元二次不等式求解集合A,由二次函数的性质求解值域,可得集合B;
(2)根据题意,可知集合C是A的真子集,分类讨论集合与两种情况,列不等式组求解.
【详解】(1)因为函数的定义域为集合A,
所以,解得,
函数,,对称轴为,
所以函数最大值为,又时,;
时,,所以最小值,
所以集合,集合
(2)∵,,且p是q的必要不充分条件,
∴集合C是A的真子集,
当时,,满足题意;
当时,得,
综上,实数m的取值范围为.
19.(1);(2)7.
【分析】(1)列举出两次掷出的点数的所有结果,再利用古典概率概率公式结合对立事件概率公式计算即得.
(2)求出,并确定事件的结果数,利用相互独立事件的概率公式求出,再逐一验证即得.
【详解】(1)将2次掷出的点数记为,则所有的样本点为:
,,,,,,,,,,,,
,,,,,,,,,,,,
,,,,,,,,,,,,
共36个,且每个样本点出现的可能性相同,
使得的样本点有,,,,,,,,,共10个,
因此,显然与为对立事件,
所以.
(2)由(1)知,,由A和B相互独立,即知,
此时等价于事件“且”,因此中仅有一个样本点,即,则,
而,,,,,
因此当且仅当时,且,所以所求m的值为7.
20.(1)(2)
【详解】(1)若时,则,
因为,在R内均单调递增,则在R内单调递增,
且,则的解集为,
即的定义域为,
令,
即,解得,
故当,函数的准不动点为.
(2)因为在内恒成立,则在内恒成立,
因为,在内均单调递增,可知在内单调递增,
且,则,解得;
令,则,
整理得,可知与在内有交点,
且,,结合的单调性可得,解得;
综上所述:实数a的取值范围为.
21.(1),,众数为70,中位数为69.4.(2)
【详解】(1)由频率分布直方图可知,解得,
,
众数为70,
因为前2组的频率和为,前3组的频率和为,
所以中位数在第3组,设中位数为m,则
,解得,
所以中位数为69.4.
(2)记3名男生分别为A,B,C,记2名女生分别为a,b,则所有抽签的情况有:
未中签AB,中签Cab;未中签AC,中签Bab;未中签Aa,中签BCb;
未中签Ab,中签BCa;未中签BC,中签Aab;未中签Ba,中签ACb;
未中签Bb,中签ACa;未中签Ca,中签ABb;未中签Cb,中签ABa;
未中签ab,中签ABC,共有10种情况,
其中中签者中男生比女生多的有:未中签Aa,中签BCb;未中签Ab,中签BCa;未中签Ba,中签ACb;未中签Bb,中签ACa;未中签Ca,中签ABb;未中签Cb,中签ABa;未中签ab,中签ABC,共7种,
所以中签者中男生比女生多的概率为.
22.【详解】(1)当时,有且定义域为,∴,
综上有:的定义域关于原点对称且,即为奇函数;
(2)时,有,即定义域为R,结论为:在R上单调递增.
设对任意两个实数:,则
,
而,,,
,∴,即得证.
(3)当时,由(2)知在R上单调递增,结合题意有,
,得,即m,n是的两个不同的实根,
令,则,在上有两个不同实根,
故,可得,
所以的范围为.
数学试题
一、单选题
1.已知,,若集合,则的值为( )
A. B. C.1 D.2
2.已知点在幂函数的图象上,设,,,则a,b,c的大小关系为( )
A. B. C. D.
3.函数的图象是( )
A. B.
C. D.
4.从某公司生产的产品中任意抽取12件,得到它们的质量(单位:kg)如下:7.9,9.0,8.9,8.6,8.4,8.5,8.5,8.5,9.9,7.8,8.3,8.0,则这组数据的四分位数不可能是( )
A.8.75 B.8.15 C.9.9 D.8.5
5.心理学家有时间用函数测定在时间t(单位:min)内能够记忆的量L,其中A表示需要记忆的量,k表示记忆率.假设一个学生需要记忆的量为200个单词,此时L表示在时间t内该生能够记忆的单词个数.已知该生在5min内能够记忆20个单词,则k的值约为( )
A.0.021 B.0.221 C.0.461 D.0.661
6.已知,若是的最小值,则实数t的取值范围为( )
A. B. C. D.
7.已知函数,正实数a,b满足,则的最大值为( )
A. B. C. D.
8.已知函数既是二次函数又是幂函数,若函数,则( )
A.2023 B.2024 C.4046 D.4047
二、多选题
9.下列说法中正确的有( )
A.命题,,则命题p的否定是,
B.“”是“”的必要条件
C.若命题“,”是真命题,则a的取值范围为
D.“”是“关于x的方程有一正一负根”的充要条件
10.已知一组样本数据,现有一组新的,则与原样本数据相比,新的样本数据( )
A.平均数不变 B.中位数不变 C.极差变小 D.方差变小
11.若函数在上满足:对任意的,当时,恒有,则称函数为“理想函数”.下列函数能被称为“理想函数”的有( )
A. B.
C. D.
12.数学上,高斯符号(Gauss mark)是指对取整符号和取小符号的统称,用于数论等领域.定义在数学特别是数论领域中,有时需要略去一个实数的小数部分只研究它的整数部分,或需要略去整数部分研究小数部分,因而引入高斯符号.设,用表示不超过x的最大整数.比如:,,,,…,已知函数,则下列说法不正确的是( )
A.的值域为 B.在为减函数
C.方程无实根 D.方程仅有一个实根
三、填空题
13.某校教师男女人数之比为,该校所有教师进行1分钟限时投篮比赛.现记录了每个教师1分钟命中次数,已知男教师命中次数的平均数为17,方差为16,女教师命中次数的平均数为8,方差为16,那么全体教师1分钟限时投篮次数的方差为______.
14.已知函数在上有一个零点,用二分法求零点的近似值(精确度为0.1)时,至少需要进行______次中点函数值的计算.
15.已知函数在上单调递增,则实数a的取值范围是______.
16设函数,给出下列四个结论:
①对,方程都有3个实数根;
②,使得;
③若互不相等的实数满足,则的取值范围是.
其中所有正确结论的序号是______.
四、解答题
17.(1)计算
(2)计算.
18,函数的定义域为集合A,集合,.
(1)求集合A,B;
(2)设,,且p是q的必要不充分条件,求实数m的取值范围.
19.抛掷一枚均匀的骰子2次,将第1次掷出的点数记为a,第2次掷出的点数记为b.
(1)求的概率;
(2)记事件A为“”,事件B为“”,若且事件A和事件B为相互独立事件,求m的值.
20.设D是函数定义域的一个子集,若存在,使得成立,则称是的一个“准不动点”,也称在区间D上存在准不动点.已知.
(1)若,求函数的准不动点;
(2)若函数在区间上存在准不动点,求实数a的取值范围.
21.第19届亚运会将于2023年9月23日至10月8日在杭州举行,而亚运会志愿者的服务工作是举办一届成功的亚运会的重要保障.为配合亚运会志愿者选拔,某高校举行了志愿者选拔面试,面试成绩满分100分,现随机抽取了80名候选者的面试成绩,绘制成如下频率分布直方图.
(1)求a的值,并估计这80名候选者面试成绩平均值,众数,中位数;(同一组中的数据用该组区间的中点值作代表,中位数精确到0.1)
(2)乒乓球项目场地志愿服务需要3名志愿者,有3名男生和2名女生通过该项志愿服务选拔,需要通过抽签的方式决定最终的人选,现将3张写有“中签”和2张写有“未中签”字样的字条随机分配给每一位候选人,求中签者中男生比女生多的概率.
22.设,函数.
(1)若,求证:函数为奇函数;
(2)若,判断并证明函数的单调性;
(3)若,函数在区间上的取值范围是,求的范围.
南阳市部分中学2023-2024学年高一上学期期末联考
数学答案
1.B 2.B 3.B 4.C 5.A 6.C 7.B
8.D 【详解】函数既是二次函数又是幂函数,∴,∴为偶函数;
因为函数是R上的奇函数,
所以为定义域R上的奇函数;
,
.故选:D.
9.ACD
10.ACD 【详解】对于A,新数据的总和为:,与原数据总和相等,且数据个数都是n,因此平均数不变,A正确;
对于B,不妨设原数据为:1,2.5,3,中位数为2.5,则新数据为:1.75,2.75,2,中位数为2,B错误;
对于C,原数据极差为:,新数据极差为:,
而,即极差变小了,C正确;
对于D,由于两组数据的平均数不变,而极差变小,说明新数据相对原数据更集中于平均数,因此方差变小,D正确.故选:ACD.
11.ABD 【详解】不妨设,则由题意可得,即,由单调性定义可知,函数在上单调递增,即若在上单调递增,则称函数为“理想函数”.
A选项中,该函数在上单调递增,符合“理想函数”的定义;
B选项中,该函数在上单调递增,符合“理想函数”的定义;
C选项中,该函数在上单调递减,不符合“理想函数”的定义;
D选项中.该函数在上单调递增,符合“理想函数”的定义.
故选:ABD.
12.AB 【详解】由高斯函数的定义可得:当时,,则,
当时,,则,当时,,则,
当时,,则,当时,,则,
绘制函数图象如图所示,
对于A,由图可知,在上的值域为,不正确;
对于B,当时,的每段函数都是单调递减,但是在不是减函数,不正确;
对于C,由选项A知,在上的值域为,
所以方程无实根,正确:
对于D,当时,即,解得,
当时,即,解得,
结合函数图象知,方程仅有一个实根,正确.
故选:AB.
13.36 14.4 15.
16.②③
【详解】当时,的图象是开口向上、对称轴为直线的抛物线在y轴及左侧部分,
当时,的图象是对数函数的图象向上平移1个单位而得,如图,
对于①,观察图象知,当时,方程只有2个实数根,①错误;
对于②,当时,使得有成立,即与有交点,
而的图象与函数的图象关于y轴对称,
显然的图象与函数的图象有公共点,②正确;
对于③,不妨设互不相等的实数且,当满足时,
由图可知,即,当,,即时,,
当,,即时,,因此,
所以,③正确,
所以所有正确结论的序号是②③.
故答案为:②③
17.(1)0;(2)3
【详解】(1)
.
(2)
.
18.(1),;
(2)
【分析】(1)根据定义域列一元二次不等式求解集合A,由二次函数的性质求解值域,可得集合B;
(2)根据题意,可知集合C是A的真子集,分类讨论集合与两种情况,列不等式组求解.
【详解】(1)因为函数的定义域为集合A,
所以,解得,
函数,,对称轴为,
所以函数最大值为,又时,;
时,,所以最小值,
所以集合,集合
(2)∵,,且p是q的必要不充分条件,
∴集合C是A的真子集,
当时,,满足题意;
当时,得,
综上,实数m的取值范围为.
19.(1);(2)7.
【分析】(1)列举出两次掷出的点数的所有结果,再利用古典概率概率公式结合对立事件概率公式计算即得.
(2)求出,并确定事件的结果数,利用相互独立事件的概率公式求出,再逐一验证即得.
【详解】(1)将2次掷出的点数记为,则所有的样本点为:
,,,,,,,,,,,,
,,,,,,,,,,,,
,,,,,,,,,,,,
共36个,且每个样本点出现的可能性相同,
使得的样本点有,,,,,,,,,共10个,
因此,显然与为对立事件,
所以.
(2)由(1)知,,由A和B相互独立,即知,
此时等价于事件“且”,因此中仅有一个样本点,即,则,
而,,,,,
因此当且仅当时,且,所以所求m的值为7.
20.(1)(2)
【详解】(1)若时,则,
因为,在R内均单调递增,则在R内单调递增,
且,则的解集为,
即的定义域为,
令,
即,解得,
故当,函数的准不动点为.
(2)因为在内恒成立,则在内恒成立,
因为,在内均单调递增,可知在内单调递增,
且,则,解得;
令,则,
整理得,可知与在内有交点,
且,,结合的单调性可得,解得;
综上所述:实数a的取值范围为.
21.(1),,众数为70,中位数为69.4.(2)
【详解】(1)由频率分布直方图可知,解得,
,
众数为70,
因为前2组的频率和为,前3组的频率和为,
所以中位数在第3组,设中位数为m,则
,解得,
所以中位数为69.4.
(2)记3名男生分别为A,B,C,记2名女生分别为a,b,则所有抽签的情况有:
未中签AB,中签Cab;未中签AC,中签Bab;未中签Aa,中签BCb;
未中签Ab,中签BCa;未中签BC,中签Aab;未中签Ba,中签ACb;
未中签Bb,中签ACa;未中签Ca,中签ABb;未中签Cb,中签ABa;
未中签ab,中签ABC,共有10种情况,
其中中签者中男生比女生多的有:未中签Aa,中签BCb;未中签Ab,中签BCa;未中签Ba,中签ACb;未中签Bb,中签ACa;未中签Ca,中签ABb;未中签Cb,中签ABa;未中签ab,中签ABC,共7种,
所以中签者中男生比女生多的概率为.
22.【详解】(1)当时,有且定义域为,∴,
综上有:的定义域关于原点对称且,即为奇函数;
(2)时,有,即定义域为R,结论为:在R上单调递增.
设对任意两个实数:,则
,
而,,,
,∴,即得证.
(3)当时,由(2)知在R上单调递增,结合题意有,
,得,即m,n是的两个不同的实根,
令,则,在上有两个不同实根,
故,可得,
所以的范围为.
同课章节目录
