7.4 二元一次方程与一次函数-鲁教版(五四制)七年级数学下册课时训练(含答案)
文档属性
| 名称 | 7.4 二元一次方程与一次函数-鲁教版(五四制)七年级数学下册课时训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 142.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-28 17:08:12 | ||
图片预览



文档简介
7.4 二元一次方程与一次函数(第1课时)
1.用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象(如图所示),则所解的二元一次方程组是( )
A. B. C. D.
2.下面四条直线,其中直线上的每一个点的坐标都是二元一次方程2x﹣3y=6的解的是( )
A.B. C.D.
3.若二元一次方程组无解,则一次函数y=3x﹣5与y=3x+1的位置关系为( )
A.平行 B.垂直 C.相交 D.重合
4.一般地,在平面直角坐标系中,任何一个二元一次方程的解可以看成是一个点的坐标,那么,以二元一次方程的解为坐标的点的全体叫做这个二元一次方程的图象.根据作图我们发现:任何一个二元一次方程的图象都是一条直线.根据这个结论,如图,如果一个点的坐标可以用来表示关于x、y的二元一次方程组的解,那么这个点是( )
M B.N C.E D.F
5.若已知方程组的解是,则直线y=kx﹣b与直线y=﹣x+a的交点坐标是 .
6.如图,一次函数y=kx+b与y=x+2的图象相交于点P(m,4),则方程组的解是 .
7.(1)请在所给的平面直角坐标系中画出一次函数y1=x﹣1和y2=﹣2x+5画出函数的图象;
(2)根据图象直接写出的解为 ;
(3)利用图象求两条直线与x轴所围成图形的面积.
8.如图,直线y=2x+6与直线L:y=kx+b交于点P(﹣1,m)
(1)求m的值.
(2)方程组的解是 .
(3)若直线y=ax+n与直线y=2x+6平行,且经过点(0,﹣2),直接写出直线y=ax+n的表达式.
7.4 二元一次方程与一次函数(第2课时)
一、选择
1.如图,直线l1、l2的交点坐标可以看作方程组( )的解.
A. B.
C. D.
2.若以二元一次方程x+2y﹣b=0的解为坐标的点(x,y)都在直线y=﹣x+b﹣1上,则常数b=( )
A. B.2 C.﹣1 D.1
二、填空
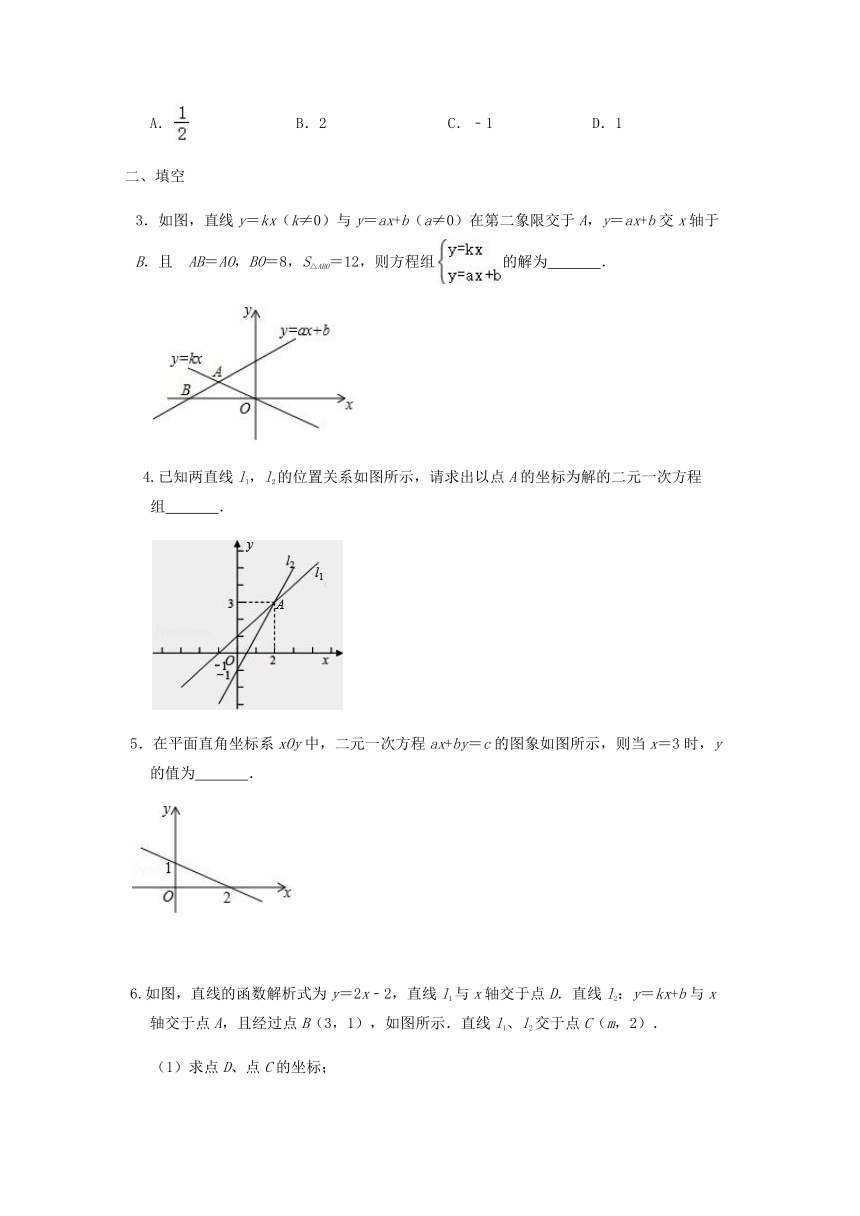
3.如图,直线y=kx(k≠0)与y=ax+b(a≠0)在第二象限交于A,y=ax+b交x轴于B.且 AB=AO,BO=8,S△ABO=12,则方程组的解为 .
4.已知两直线l1,l2的位置关系如图所示,请求出以点A的坐标为解的二元一次方程组 .
5.在平面直角坐标系xOy中,二元一次方程ax+by=c的图象如图所示,则当x=3时,y的值为 .
6.如图,直线的函数解析式为y=2x﹣2,直线l1与x轴交于点D.直线l2:y=kx+b与x轴交于点A,且经过点B(3,1),如图所示.直线l1、l2交于点C(m,2).
(1)求点D、点C的坐标;
(2)求直线l2的函数解析式;
(3)利用函数图象写出关于x、y的二元一次方程组的解.
7.4 二元一次方程与一次函数(第2课时)
A 2.B
3. 4.
5.解:从图象可以得到,
和是二元一次方程ax+by=c的两组解,
∴2a=c,b=c, ∴x+2y=2,
当x=3时,y=﹣,
故答案为﹣.
6.解:(1)∵点D为直线l1:y=2x﹣2与x轴的交点,
∴y=0,0=2x﹣2,解得x=1,∴D(1,0);
∵点C在直线l1:y=2x﹣2上,
∴2=2m﹣2,解得m=2,∴点C的坐标为(2,2);
(2)∵点C(2,2)、B(3,1)在直线l2上,
∴,解得,
∴直线l2的解析式为y=﹣x+4;
(3)由图可知二元一次方程组的解为.
7.4 二元一次方程与一次函数(第1课时)
1.B 2.D 3.A 4.C 5. (﹣1,3 )
6.
7.解:(1)如图,
(2)的解为;
(3)解方程﹣2x+5=0得x=,则直线
y=﹣2x+5与x轴的交点坐标为(,0),
解方程x﹣1=0得x=1,则直线y=x﹣1与x轴的交点坐标为(1,0),
所以两条直线与x轴所围成图形的面积=×(﹣1)×1=.
8.解:(1)∵直线y=2x+6与直线L:y=kx+b交于点P(﹣1,m),
∴把P点的坐标代入y=2x+6得:m=2×(﹣1)+6=4,即m=4;
(2)∵直线y=2x+6与直线L:y=kx+b交于点P的坐标为(﹣1,4),
∴方程组的解是,
(3)∵直线y=ax+n与直线y=2x+6平行,∴a=2,
即y=2x+n,
∵直线y=ax+n经过点(0,﹣2),
∴代入得:﹣2=0+n,
解得:n=﹣2,
即直线y=ax+n的表达式是y=2x﹣2.
1.用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象(如图所示),则所解的二元一次方程组是( )
A. B. C. D.
2.下面四条直线,其中直线上的每一个点的坐标都是二元一次方程2x﹣3y=6的解的是( )
A.B. C.D.
3.若二元一次方程组无解,则一次函数y=3x﹣5与y=3x+1的位置关系为( )
A.平行 B.垂直 C.相交 D.重合
4.一般地,在平面直角坐标系中,任何一个二元一次方程的解可以看成是一个点的坐标,那么,以二元一次方程的解为坐标的点的全体叫做这个二元一次方程的图象.根据作图我们发现:任何一个二元一次方程的图象都是一条直线.根据这个结论,如图,如果一个点的坐标可以用来表示关于x、y的二元一次方程组的解,那么这个点是( )
M B.N C.E D.F
5.若已知方程组的解是,则直线y=kx﹣b与直线y=﹣x+a的交点坐标是 .
6.如图,一次函数y=kx+b与y=x+2的图象相交于点P(m,4),则方程组的解是 .
7.(1)请在所给的平面直角坐标系中画出一次函数y1=x﹣1和y2=﹣2x+5画出函数的图象;
(2)根据图象直接写出的解为 ;
(3)利用图象求两条直线与x轴所围成图形的面积.
8.如图,直线y=2x+6与直线L:y=kx+b交于点P(﹣1,m)
(1)求m的值.
(2)方程组的解是 .
(3)若直线y=ax+n与直线y=2x+6平行,且经过点(0,﹣2),直接写出直线y=ax+n的表达式.
7.4 二元一次方程与一次函数(第2课时)
一、选择
1.如图,直线l1、l2的交点坐标可以看作方程组( )的解.
A. B.
C. D.
2.若以二元一次方程x+2y﹣b=0的解为坐标的点(x,y)都在直线y=﹣x+b﹣1上,则常数b=( )
A. B.2 C.﹣1 D.1
二、填空
3.如图,直线y=kx(k≠0)与y=ax+b(a≠0)在第二象限交于A,y=ax+b交x轴于B.且 AB=AO,BO=8,S△ABO=12,则方程组的解为 .
4.已知两直线l1,l2的位置关系如图所示,请求出以点A的坐标为解的二元一次方程组 .
5.在平面直角坐标系xOy中,二元一次方程ax+by=c的图象如图所示,则当x=3时,y的值为 .
6.如图,直线的函数解析式为y=2x﹣2,直线l1与x轴交于点D.直线l2:y=kx+b与x轴交于点A,且经过点B(3,1),如图所示.直线l1、l2交于点C(m,2).
(1)求点D、点C的坐标;
(2)求直线l2的函数解析式;
(3)利用函数图象写出关于x、y的二元一次方程组的解.
7.4 二元一次方程与一次函数(第2课时)
A 2.B
3. 4.
5.解:从图象可以得到,
和是二元一次方程ax+by=c的两组解,
∴2a=c,b=c, ∴x+2y=2,
当x=3时,y=﹣,
故答案为﹣.
6.解:(1)∵点D为直线l1:y=2x﹣2与x轴的交点,
∴y=0,0=2x﹣2,解得x=1,∴D(1,0);
∵点C在直线l1:y=2x﹣2上,
∴2=2m﹣2,解得m=2,∴点C的坐标为(2,2);
(2)∵点C(2,2)、B(3,1)在直线l2上,
∴,解得,
∴直线l2的解析式为y=﹣x+4;
(3)由图可知二元一次方程组的解为.
7.4 二元一次方程与一次函数(第1课时)
1.B 2.D 3.A 4.C 5. (﹣1,3 )
6.
7.解:(1)如图,
(2)的解为;
(3)解方程﹣2x+5=0得x=,则直线
y=﹣2x+5与x轴的交点坐标为(,0),
解方程x﹣1=0得x=1,则直线y=x﹣1与x轴的交点坐标为(1,0),
所以两条直线与x轴所围成图形的面积=×(﹣1)×1=.
8.解:(1)∵直线y=2x+6与直线L:y=kx+b交于点P(﹣1,m),
∴把P点的坐标代入y=2x+6得:m=2×(﹣1)+6=4,即m=4;
(2)∵直线y=2x+6与直线L:y=kx+b交于点P的坐标为(﹣1,4),
∴方程组的解是,
(3)∵直线y=ax+n与直线y=2x+6平行,∴a=2,
即y=2x+n,
∵直线y=ax+n经过点(0,﹣2),
∴代入得:﹣2=0+n,
解得:n=﹣2,
即直线y=ax+n的表达式是y=2x﹣2.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
