北师大版(2019)必修一 第六章 统计 章节测试题(含解析)
文档属性
| 名称 | 北师大版(2019)必修一 第六章 统计 章节测试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 782.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-27 19:00:38 | ||
图片预览



文档简介
北师大版(2019)必修一 第六章 统计 章节测试题
学校:___________姓名:___________班级:___________考号:___________
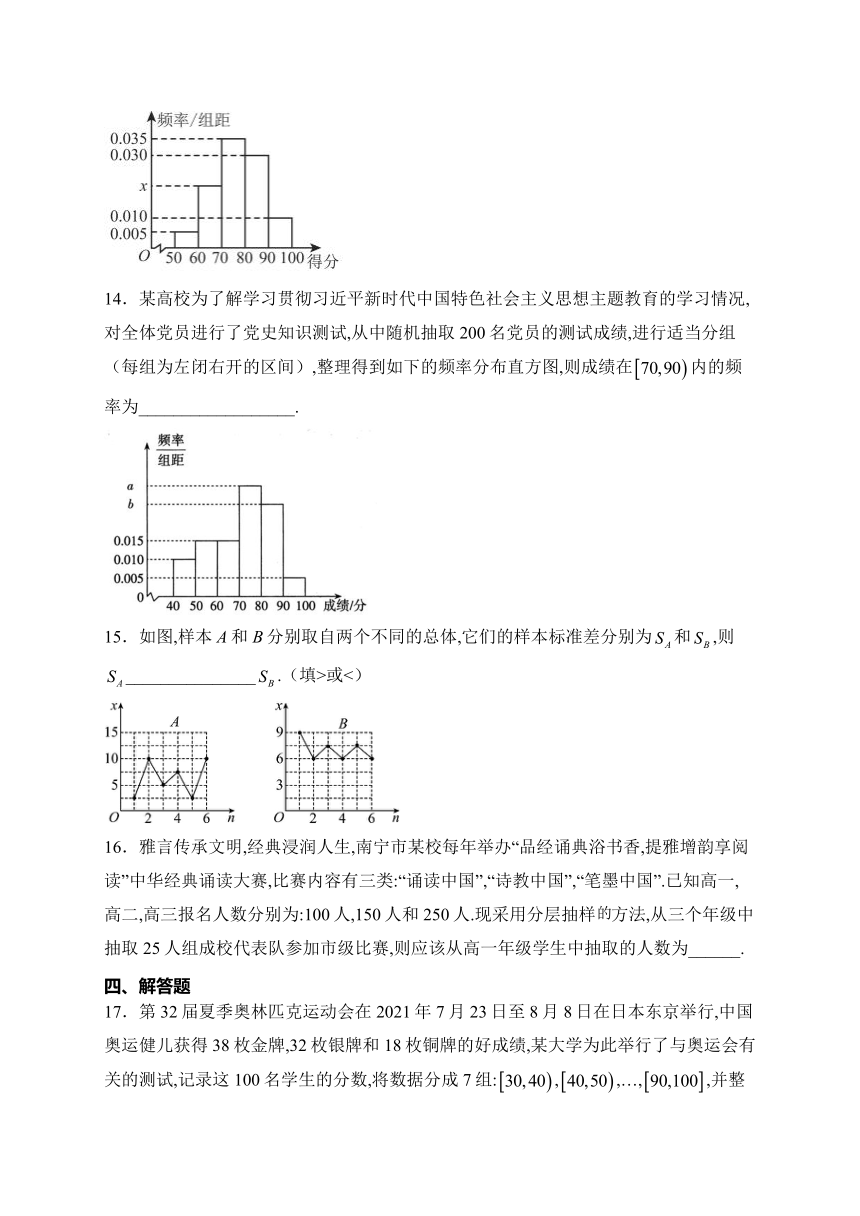
一、选择题
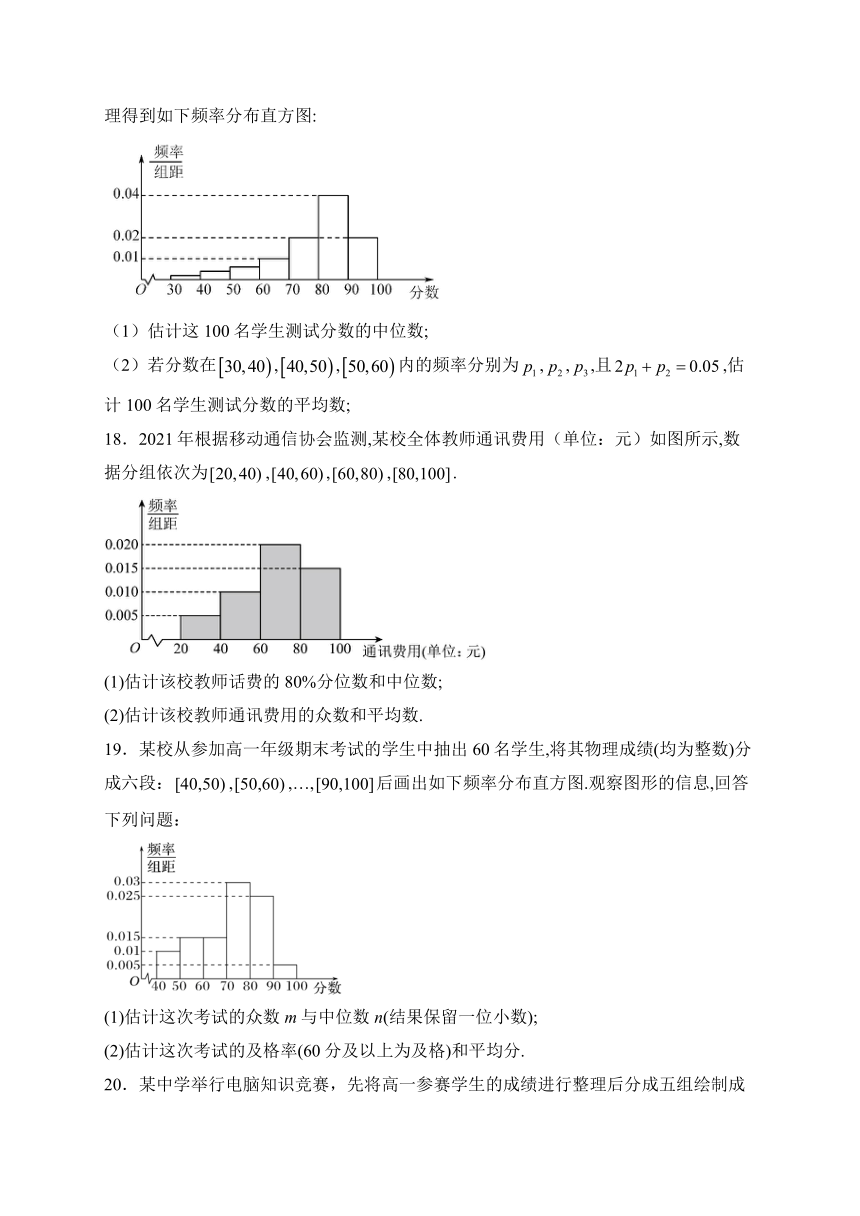
1.设一组样本数据,,…,的方差为0.01,则数据,,…,的方差为( )
A.0.01 B.0.1 C.1 D.10
2.某班全体学生参加一次测试,将所得分数依次分组:,,,,绘制出如图所示的成绩频率分布直方图.若低于60分的人数是18,则该班的学生人数是( )
A.50 B.54 C.60 D.64
3.为庆祝中国共产党成立100周年,某市举办“红歌大传唱”主题活动,以传承红色革命精神,践行社会主义路线,某高中分别有高一、高二、高三学生600人、500人、700人,欲采用分层抽样法组建一个18人的高一、高二、高三的红歌传唱队,则应抽取高三学生( )
A.5人 B.6人 C.7人 D.8人
4.已知甲,乙两名运动员进行射击比赛,每名运动员射击10次,得分情况如下图所示.则根据本次比赛结果,以下说法正确的是( )
乙射击环数 6 7 8 9 10
频数 1 2 2 2 3
A.甲比乙的射击水平更高
B.甲的射击水平更稳定
C.甲射击成绩的中位数大于乙射击成绩的中位数
D.甲射击成绩的众数大于乙射击成绩的众数
5.已知数据,,···,的平均数为,设为该组数据的“阶方差”,若,则与的大小关系为( )
A. B. C. D.与奇偶性有关
6.某大学共有教师1000人,其中教授、副教授、讲师、助教的人数比为,现用分层抽样的方法从全校所有教师中抽取一个容量为40的样本,如果样本按比例分配,那么讲师应抽取的人数为( )
A.16 B.12 C.8 D.4
7.某学习小组用计算机软件对一组数据进行回归分析,甲同学首先求出回归直线方程,样本点的中心为.乙同学对甲的计算过程进行检查,发现甲将数据误输成,数据误输成,将这两个数据修正后得到回归直线方程,则实数( )
A. B. C. D.
8.2021年某省高考体育百米测试中,成绩全部介于12秒与18秒之间,抽取其中100个样本,将测试结果按如下方式分成六组:第一组,第二组,…,第六组,得到如下频率分布直方图,则该100名考生的成绩的平均数和中位数(保留一位小数)分别是( )
A.15.2,15.4 B.15.1,15.4 C.15.1,15.3 D.15.2,15.3
二、多项选择题
9.某单位为了解职工健康情况,采用分层随机抽样的方法从5000名职工中抽取了一个容量为100的样本.其中,男性平均体重为64千克,方差为151;女性平均体重为56千克,方差为159,男女人数之比为,下列说法正确的是( )
A.样本为该单位的职工 B.每一位职工被抽中的可能性为
C.该单位职工平均体重 D.单位职工的方差
10.气象意义上从春季进入夏季的标志为连续5天的日平均温度均不低于℃,现有甲,乙,丙,丁四地连续5天的日平均温度的记录数据的部分信息(记录数据都是正整数).依据以下信息,能确定进入夏季地区的选项有( )
A.甲地5个数据的中位数为24,众数为22
B.乙地5个数据的中位数为25,平均数为24
C.丙地5个数据的平均数为22,众数为22
D.丁地5个数据中有一个数据是28,平均数为24,方差为4.8
11.一组样本数据,,…,的平均数为,标准差为s.另一组样本数据,,…,,的平均数为,标准差为s.两组数据合成一组新数据,,…,,,…,,新数据的平均数为,标准差为,则( )
A. B. C. D.
12.统计学是源自对国家的资料进行分析,也就是“研究国家的科学”.一般认为其学理研究始于希腊的亚里士多德时代,迄今已有两千三百多年的历史.在两千多年的发展过程中,将社会经济现象量化的方法是近代统计学的重要特征.为此,统计学有了自己研究问题的参数,比如:均值,中位数,众数,标准差.一组数据:,,…,()记其均值为m,中位数为k,方差为,则( )
A.
B.
C.新数据:,,,…,的均值为
D.新数据:,,,…,的方差为
三、填空题
13.2022年12月4日是第九个国家宪法日,主题为“学习宣传贯彻党的二十大精神,推动全面贯彻实施宪法”,某校由学生会同学制作了宪法学习问卷,收获了有效答卷2000份,先对其得分情况进行了统计,按照、、…、分成5组,并绘制了如图所示的频率分布直方图,则图中_________.
14.某高校为了解学习贯彻习近平新时代中国特色社会主义思想主题教育的学习情况,对全体党员进行了党史知识测试,从中随机抽取200名党员的测试成绩,进行适当分组(每组为左闭右开的区间),整理得到如下的频率分布直方图,则成绩在内的频率为__________________.
15.如图,样本A和B分别取自两个不同的总体,它们的样本标准差分别为和,则_______________.(填>或<)
16.雅言传承文明,经典浸润人生,南宁市某校每年举办“品经诵典浴书香,提雅增韵享阅读”中华经典诵读大赛,比赛内容有三类:“诵读中国”,“诗教中国”,“笔墨中国”.已知高一,高二,高三报名人数分别为:100人,150人和250人.现采用分层抽样方法,从三个年级中抽取25人组成校代表队参加市级比赛,则应该从高一年级学生中抽取的人数为______.
四、解答题
17.第32届夏季奥林匹克运动会在2021年7月23日至8月8日在日本东京举行,中国奥运健儿获得38枚金牌,32枚银牌和18枚铜牌的好成绩,某大学为此举行了与奥运会有关的测试,记录这100名学生的分数,将数据分成7组:,,…,,并整理得到如下频率分布直方图:
(1)估计这100名学生测试分数的中位数;
(2)若分数在,,内的频率分别为,,,且,估计100名学生测试分数的平均数;
18.2021年根据移动通信协会监测,某校全体教师通讯费用(单位:元)如图所示,数据分组依次为,,,.
(1)估计该校教师话费的80%分位数和中位数;
(2)估计该校教师通讯费用的众数和平均数.
19.某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段:,,…,后画出如下频率分布直方图.观察图形的信息,回答下列问题:
(1)估计这次考试的众数m与中位数n(结果保留一位小数);
(2)估计这次考试的及格率(60分及以上为及格)和平均分.
20.某中学举行电脑知识竞赛,先将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图.
(1)求参赛学生成绩的众数、中位数;
(2)高一参赛学生的平均成绩;
(3)按分层抽样的方法从中抽取6名学生,再从这6人中,抽取2人,则求这两人都是在的概率.
21.为了解学生的周末学习时间(单位:小时),高一年级某班班主任对本班名学生某周末的学习时间进行了调查,将所得数据整理绘制出如图所示的频率分布直方图,根据直方图所提供的信息:
(1)求该班学生周末的学习时间不少于20小时的人数;
(2)估计这40名同学周末学习时间的分位数;
(3)如果用该班学生周末的学习时间作为样本去推断该校高一年级全体学生周末的学习时间,这样推断是否合理?说明理由.
22.1995年,联合国教科文组织宣布4月23日为世界读书日,向全世界发出了走向阅读社会的号召,4月也因此成为“读书月”。定这个日期是因为,1616年4月23日是西班牙著名作家塞万提斯和英国著名作家莎士比亚的辞世纪念日。某校为了解高一学生在“读书月”课外阅读时间的情况,抽样调查了其中的100名学生,统计他们阅读的时间(单位:小时),并将统计数据绘制成如图的频率分布直方图.
(1)估计这100名学生在“读书月”课外阅读时间的众数,中位数,平均数;
(2)估计这100名学生在这个“读书月”内课外阅读时间的第75百分位数(结果保留两位小数).
参考答案
1.答案:C
解析:因为数据的方差是数据的方差的倍,
所以所求数据方差为
故选:C
2.答案:C
解析:由题中频率分布直方图可知,得分低于60分的频率为.低于60分的人数是18,该班的学生人数是.故选C.
3.答案:C
解析:依题意知应抽取的高三学生的人数为.故选C.
4.答案:B
解析:甲的平均数
乙的平均数
,乙的射击水平更高,故A错误;
甲的方差
乙的方差
,甲的射击水平更稳定,故B正确;
甲的射击成绩由小到大排列为:5,7,8,8,8,9,9,9,9,10,位于第5、第6位的数分别是8,9,
所以甲的中位数是;乙的射击成绩由小到大排列为:6,7,7,8,8,9,9,10,10,10,
位于第5、第6位的数分别是8,9,所以乙的中位数是,
故甲射击成绩的中位数与乙射击成绩的中位数相等,故C错误;
甲的众数为9,乙的众数为10,故D错误.
故选:B.
5.答案:A
解析:因为,所以,
因为,且,
所以当为偶数时,为偶数,所以,
当时,;
当时,则,所以,
综上,,
所以,
当为奇数时,为奇数,所以,
当时,;
当时,则,
所以,
综上,,
所以,
综上所述:.
故选:A.
6.答案:B
解析:根据分层抽样的方法,样本按比例分配,讲师应抽取的人数为,
故选:B.
7.答案:D
解析:由题可知,假设甲输入的为,为,
所以,,所以,,
改为正确数据时得,,
所以样本点的中心为,将其代入回归直线方程,得.
故选:D.
8.答案:C
解析:100名考生成绩的平均数,
因为前三组面积和为,
前四组面积和为,
所以中位数位于第四组内,设中位数为a,
则有,
解得,
故选:C.
9.答案:BCD
解析:
10.答案:AD
解析:对于A:因为众数为22,中位数为24,所以22出现了两次,
若有一天低于22,则中位数不可能为24,
所以另两个数据均大于24(且不相等),故甲地一定进入夏季,故A正确;
对于B:若乙地区的数据从小到大依次为18,23,25,26,28,
满足中位数为25,平均数为24,但是乙地不一定进入夏季,故B错误;
对于C:若丙地区的数据从小到大依次为,,,,,
满足平均数为22,众数为22,但是丙地不一定进入夏季,故C错误;
对于D:设其余4个数据分别为a,b,c,d(正整数),则,
所以,
若a,b,c,d(正整数)中有一个数据小于,则,不符合题意,
故a,b,c,d(正整数)均不小于,故丁地区进入夏季,故D正确;
故选:AD
11.答案:BC
解析:由题意,
,
同理
两式相加得,
,
所以,.
故选:BC.
12.答案:CD
解析:对于A选项,因
样本数据最中间的项为和,
由中位数的定义可知,,A错;
对于B,不妨令,
故不成立,故B错误;对于C,数据,,,的均值为:
,C正确;
对于D,数据,,,…,的均值为:
其方差为,D对.
故选:CD.
13.答案:0.020
解析:由频率分布直方图的性质可得,
解得,故答案为0.020.
14.答案:0.55
解析:由频率分布直方图知:,,
则成绩在内的频率为
故答案为:0.55.
15.答案:>
解析:从图中可以看出图A的波动比较大,图B波动比较小,所以.具体计算如下:
样本A提取数据:2.5,10,5,7.5,2.5,10.
样本A的平均数为,
样本标准差,
样本B提取数据:15,10,12.5,10,12.5,10.
样本B的平均数为;
样本标准差
..
故答案为:>.
16.答案:5
解析:根据题意可得:高一,高二,高三报名人数之比为,
故从高一年级学生中抽取的人数为.
故答案为:5.
17.答案:(1)82.5分
(2)79.5分
解析:(1)设这100名学生测试分数的中位数为,由前5组频率之和为0.4,前6组频率之和为0.8,
可得,所以,解得.
故这100名学生测试分数的中位数约为82.5分.
(2)因为,且,所以这100名学生测试分数的平均数为
.
故100名学生测试分数的平均数约为79.5分.
18.答案:(1)80%分位数为,中位数为70
(2)众数为70,平均数为
解析:(1)该校教师话费在80元以下的频率为:,
该校教师话费在的频率为0.3,因此,该校教师话费的80%分位数在内.
由.可以估计该校教师话费的80%分位数为.
设中位数为,所以.
(2)该校教师通讯费用的众数为70;平均数为:.
19.答案:(1)73.3
(2)合格率是75% 平均分是71分
解析:(1)众数是最高小矩形底边中点的横坐标,
众数为.
前三个小矩形面积为.
中位数平分直方图的面积,
.
(2)依题意60分及以上的分数所在的第三、四、五、六组的频率和为
,
抽样学生成绩的合格率是75%.
利用组中值估算抽样学生的平均分为
.
估计这次考试的平均分是71分.
20.答案:(1)众数为65,中位数为
(2)67
(3)
解析:(1)
由题图可知众数为65,
因为的频率为;的频率为;
的频率为;的频率为;
的频率为;
所以设中位数为,则,解得,所以中位数为;
(2)由(1)可得,平均成绩为,
所以平均成绩为67;
(3)按分层抽样的方法从中抽取6名学生,则分别抽取了3人,2人,1人.
设这6人分别为.
再从其中抽取2人,这一共有,总共15种情况.
两人都在有三种情况,
则求这两人都是在的概率为.
21.答案:(1)9;
(2)8.75;
(3)不合理,样本的选取只选在高一某班,不具有代表性.
解析:(1)由图可知,该班学生周末的学习时间不少于20小时的频率为
则40名学生中周末的学习时间不少于20小时的人数为.
(2)学习时间在小时以下的频率为,
学习时间在小时以下的频率为,
所以分位数在,,则这40名同学周末学习时间的分位数为8.75.
(3)不合理,样本的选取只选在高一某班,不具有代表性.
22.答案:(1)20.32
(2)23.86
解析:(1)由频率分布直方图可看出最高矩形底边上的中点值为20,故众数是20;
由,解得,
,且,
中位数位于之间,设中位数为x,
,解得,故中位数是20.4;
平均数为;
(2)75百分位数即为上四分位数,
又,,
上四分位数位于之间,设上四分位数为y,
则,解得.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.设一组样本数据,,…,的方差为0.01,则数据,,…,的方差为( )
A.0.01 B.0.1 C.1 D.10
2.某班全体学生参加一次测试,将所得分数依次分组:,,,,绘制出如图所示的成绩频率分布直方图.若低于60分的人数是18,则该班的学生人数是( )
A.50 B.54 C.60 D.64
3.为庆祝中国共产党成立100周年,某市举办“红歌大传唱”主题活动,以传承红色革命精神,践行社会主义路线,某高中分别有高一、高二、高三学生600人、500人、700人,欲采用分层抽样法组建一个18人的高一、高二、高三的红歌传唱队,则应抽取高三学生( )
A.5人 B.6人 C.7人 D.8人
4.已知甲,乙两名运动员进行射击比赛,每名运动员射击10次,得分情况如下图所示.则根据本次比赛结果,以下说法正确的是( )
乙射击环数 6 7 8 9 10
频数 1 2 2 2 3
A.甲比乙的射击水平更高
B.甲的射击水平更稳定
C.甲射击成绩的中位数大于乙射击成绩的中位数
D.甲射击成绩的众数大于乙射击成绩的众数
5.已知数据,,···,的平均数为,设为该组数据的“阶方差”,若,则与的大小关系为( )
A. B. C. D.与奇偶性有关
6.某大学共有教师1000人,其中教授、副教授、讲师、助教的人数比为,现用分层抽样的方法从全校所有教师中抽取一个容量为40的样本,如果样本按比例分配,那么讲师应抽取的人数为( )
A.16 B.12 C.8 D.4
7.某学习小组用计算机软件对一组数据进行回归分析,甲同学首先求出回归直线方程,样本点的中心为.乙同学对甲的计算过程进行检查,发现甲将数据误输成,数据误输成,将这两个数据修正后得到回归直线方程,则实数( )
A. B. C. D.
8.2021年某省高考体育百米测试中,成绩全部介于12秒与18秒之间,抽取其中100个样本,将测试结果按如下方式分成六组:第一组,第二组,…,第六组,得到如下频率分布直方图,则该100名考生的成绩的平均数和中位数(保留一位小数)分别是( )
A.15.2,15.4 B.15.1,15.4 C.15.1,15.3 D.15.2,15.3
二、多项选择题
9.某单位为了解职工健康情况,采用分层随机抽样的方法从5000名职工中抽取了一个容量为100的样本.其中,男性平均体重为64千克,方差为151;女性平均体重为56千克,方差为159,男女人数之比为,下列说法正确的是( )
A.样本为该单位的职工 B.每一位职工被抽中的可能性为
C.该单位职工平均体重 D.单位职工的方差
10.气象意义上从春季进入夏季的标志为连续5天的日平均温度均不低于℃,现有甲,乙,丙,丁四地连续5天的日平均温度的记录数据的部分信息(记录数据都是正整数).依据以下信息,能确定进入夏季地区的选项有( )
A.甲地5个数据的中位数为24,众数为22
B.乙地5个数据的中位数为25,平均数为24
C.丙地5个数据的平均数为22,众数为22
D.丁地5个数据中有一个数据是28,平均数为24,方差为4.8
11.一组样本数据,,…,的平均数为,标准差为s.另一组样本数据,,…,,的平均数为,标准差为s.两组数据合成一组新数据,,…,,,…,,新数据的平均数为,标准差为,则( )
A. B. C. D.
12.统计学是源自对国家的资料进行分析,也就是“研究国家的科学”.一般认为其学理研究始于希腊的亚里士多德时代,迄今已有两千三百多年的历史.在两千多年的发展过程中,将社会经济现象量化的方法是近代统计学的重要特征.为此,统计学有了自己研究问题的参数,比如:均值,中位数,众数,标准差.一组数据:,,…,()记其均值为m,中位数为k,方差为,则( )
A.
B.
C.新数据:,,,…,的均值为
D.新数据:,,,…,的方差为
三、填空题
13.2022年12月4日是第九个国家宪法日,主题为“学习宣传贯彻党的二十大精神,推动全面贯彻实施宪法”,某校由学生会同学制作了宪法学习问卷,收获了有效答卷2000份,先对其得分情况进行了统计,按照、、…、分成5组,并绘制了如图所示的频率分布直方图,则图中_________.
14.某高校为了解学习贯彻习近平新时代中国特色社会主义思想主题教育的学习情况,对全体党员进行了党史知识测试,从中随机抽取200名党员的测试成绩,进行适当分组(每组为左闭右开的区间),整理得到如下的频率分布直方图,则成绩在内的频率为__________________.
15.如图,样本A和B分别取自两个不同的总体,它们的样本标准差分别为和,则_______________.(填>或<)
16.雅言传承文明,经典浸润人生,南宁市某校每年举办“品经诵典浴书香,提雅增韵享阅读”中华经典诵读大赛,比赛内容有三类:“诵读中国”,“诗教中国”,“笔墨中国”.已知高一,高二,高三报名人数分别为:100人,150人和250人.现采用分层抽样方法,从三个年级中抽取25人组成校代表队参加市级比赛,则应该从高一年级学生中抽取的人数为______.
四、解答题
17.第32届夏季奥林匹克运动会在2021年7月23日至8月8日在日本东京举行,中国奥运健儿获得38枚金牌,32枚银牌和18枚铜牌的好成绩,某大学为此举行了与奥运会有关的测试,记录这100名学生的分数,将数据分成7组:,,…,,并整理得到如下频率分布直方图:
(1)估计这100名学生测试分数的中位数;
(2)若分数在,,内的频率分别为,,,且,估计100名学生测试分数的平均数;
18.2021年根据移动通信协会监测,某校全体教师通讯费用(单位:元)如图所示,数据分组依次为,,,.
(1)估计该校教师话费的80%分位数和中位数;
(2)估计该校教师通讯费用的众数和平均数.
19.某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段:,,…,后画出如下频率分布直方图.观察图形的信息,回答下列问题:
(1)估计这次考试的众数m与中位数n(结果保留一位小数);
(2)估计这次考试的及格率(60分及以上为及格)和平均分.
20.某中学举行电脑知识竞赛,先将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图.
(1)求参赛学生成绩的众数、中位数;
(2)高一参赛学生的平均成绩;
(3)按分层抽样的方法从中抽取6名学生,再从这6人中,抽取2人,则求这两人都是在的概率.
21.为了解学生的周末学习时间(单位:小时),高一年级某班班主任对本班名学生某周末的学习时间进行了调查,将所得数据整理绘制出如图所示的频率分布直方图,根据直方图所提供的信息:
(1)求该班学生周末的学习时间不少于20小时的人数;
(2)估计这40名同学周末学习时间的分位数;
(3)如果用该班学生周末的学习时间作为样本去推断该校高一年级全体学生周末的学习时间,这样推断是否合理?说明理由.
22.1995年,联合国教科文组织宣布4月23日为世界读书日,向全世界发出了走向阅读社会的号召,4月也因此成为“读书月”。定这个日期是因为,1616年4月23日是西班牙著名作家塞万提斯和英国著名作家莎士比亚的辞世纪念日。某校为了解高一学生在“读书月”课外阅读时间的情况,抽样调查了其中的100名学生,统计他们阅读的时间(单位:小时),并将统计数据绘制成如图的频率分布直方图.
(1)估计这100名学生在“读书月”课外阅读时间的众数,中位数,平均数;
(2)估计这100名学生在这个“读书月”内课外阅读时间的第75百分位数(结果保留两位小数).
参考答案
1.答案:C
解析:因为数据的方差是数据的方差的倍,
所以所求数据方差为
故选:C
2.答案:C
解析:由题中频率分布直方图可知,得分低于60分的频率为.低于60分的人数是18,该班的学生人数是.故选C.
3.答案:C
解析:依题意知应抽取的高三学生的人数为.故选C.
4.答案:B
解析:甲的平均数
乙的平均数
,乙的射击水平更高,故A错误;
甲的方差
乙的方差
,甲的射击水平更稳定,故B正确;
甲的射击成绩由小到大排列为:5,7,8,8,8,9,9,9,9,10,位于第5、第6位的数分别是8,9,
所以甲的中位数是;乙的射击成绩由小到大排列为:6,7,7,8,8,9,9,10,10,10,
位于第5、第6位的数分别是8,9,所以乙的中位数是,
故甲射击成绩的中位数与乙射击成绩的中位数相等,故C错误;
甲的众数为9,乙的众数为10,故D错误.
故选:B.
5.答案:A
解析:因为,所以,
因为,且,
所以当为偶数时,为偶数,所以,
当时,;
当时,则,所以,
综上,,
所以,
当为奇数时,为奇数,所以,
当时,;
当时,则,
所以,
综上,,
所以,
综上所述:.
故选:A.
6.答案:B
解析:根据分层抽样的方法,样本按比例分配,讲师应抽取的人数为,
故选:B.
7.答案:D
解析:由题可知,假设甲输入的为,为,
所以,,所以,,
改为正确数据时得,,
所以样本点的中心为,将其代入回归直线方程,得.
故选:D.
8.答案:C
解析:100名考生成绩的平均数,
因为前三组面积和为,
前四组面积和为,
所以中位数位于第四组内,设中位数为a,
则有,
解得,
故选:C.
9.答案:BCD
解析:
10.答案:AD
解析:对于A:因为众数为22,中位数为24,所以22出现了两次,
若有一天低于22,则中位数不可能为24,
所以另两个数据均大于24(且不相等),故甲地一定进入夏季,故A正确;
对于B:若乙地区的数据从小到大依次为18,23,25,26,28,
满足中位数为25,平均数为24,但是乙地不一定进入夏季,故B错误;
对于C:若丙地区的数据从小到大依次为,,,,,
满足平均数为22,众数为22,但是丙地不一定进入夏季,故C错误;
对于D:设其余4个数据分别为a,b,c,d(正整数),则,
所以,
若a,b,c,d(正整数)中有一个数据小于,则,不符合题意,
故a,b,c,d(正整数)均不小于,故丁地区进入夏季,故D正确;
故选:AD
11.答案:BC
解析:由题意,
,
同理
两式相加得,
,
所以,.
故选:BC.
12.答案:CD
解析:对于A选项,因
样本数据最中间的项为和,
由中位数的定义可知,,A错;
对于B,不妨令,
故不成立,故B错误;对于C,数据,,,的均值为:
,C正确;
对于D,数据,,,…,的均值为:
其方差为,D对.
故选:CD.
13.答案:0.020
解析:由频率分布直方图的性质可得,
解得,故答案为0.020.
14.答案:0.55
解析:由频率分布直方图知:,,
则成绩在内的频率为
故答案为:0.55.
15.答案:>
解析:从图中可以看出图A的波动比较大,图B波动比较小,所以.具体计算如下:
样本A提取数据:2.5,10,5,7.5,2.5,10.
样本A的平均数为,
样本标准差,
样本B提取数据:15,10,12.5,10,12.5,10.
样本B的平均数为;
样本标准差
..
故答案为:>.
16.答案:5
解析:根据题意可得:高一,高二,高三报名人数之比为,
故从高一年级学生中抽取的人数为.
故答案为:5.
17.答案:(1)82.5分
(2)79.5分
解析:(1)设这100名学生测试分数的中位数为,由前5组频率之和为0.4,前6组频率之和为0.8,
可得,所以,解得.
故这100名学生测试分数的中位数约为82.5分.
(2)因为,且,所以这100名学生测试分数的平均数为
.
故100名学生测试分数的平均数约为79.5分.
18.答案:(1)80%分位数为,中位数为70
(2)众数为70,平均数为
解析:(1)该校教师话费在80元以下的频率为:,
该校教师话费在的频率为0.3,因此,该校教师话费的80%分位数在内.
由.可以估计该校教师话费的80%分位数为.
设中位数为,所以.
(2)该校教师通讯费用的众数为70;平均数为:.
19.答案:(1)73.3
(2)合格率是75% 平均分是71分
解析:(1)众数是最高小矩形底边中点的横坐标,
众数为.
前三个小矩形面积为.
中位数平分直方图的面积,
.
(2)依题意60分及以上的分数所在的第三、四、五、六组的频率和为
,
抽样学生成绩的合格率是75%.
利用组中值估算抽样学生的平均分为
.
估计这次考试的平均分是71分.
20.答案:(1)众数为65,中位数为
(2)67
(3)
解析:(1)
由题图可知众数为65,
因为的频率为;的频率为;
的频率为;的频率为;
的频率为;
所以设中位数为,则,解得,所以中位数为;
(2)由(1)可得,平均成绩为,
所以平均成绩为67;
(3)按分层抽样的方法从中抽取6名学生,则分别抽取了3人,2人,1人.
设这6人分别为.
再从其中抽取2人,这一共有,总共15种情况.
两人都在有三种情况,
则求这两人都是在的概率为.
21.答案:(1)9;
(2)8.75;
(3)不合理,样本的选取只选在高一某班,不具有代表性.
解析:(1)由图可知,该班学生周末的学习时间不少于20小时的频率为
则40名学生中周末的学习时间不少于20小时的人数为.
(2)学习时间在小时以下的频率为,
学习时间在小时以下的频率为,
所以分位数在,,则这40名同学周末学习时间的分位数为8.75.
(3)不合理,样本的选取只选在高一某班,不具有代表性.
22.答案:(1)20.32
(2)23.86
解析:(1)由频率分布直方图可看出最高矩形底边上的中点值为20,故众数是20;
由,解得,
,且,
中位数位于之间,设中位数为x,
,解得,故中位数是20.4;
平均数为;
(2)75百分位数即为上四分位数,
又,,
上四分位数位于之间,设上四分位数为y,
则,解得.
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
