数学人教A版(2019)选择性必修第三册8.2一元线性回归模型 课件(共31张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册8.2一元线性回归模型 课件(共31张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-27 21:14:45 | ||
图片预览










文档简介
(共31张PPT)
第八章
成对数据的统计分析
8.2一元线性回归模型及应用
通过前面的学习我们已经了解到,根据成对样本数据的散点图和样本相关系数,可以推断两个变量是否存在相关关系、是正相关还是负相关,以及线性相关程度的强弱等.
思考:是否能像建立函数模型刻画两个变量之间的确定性关系那样,通过建立适当的统计模型来刻画两变量之间的相关关系呢?
新课引入
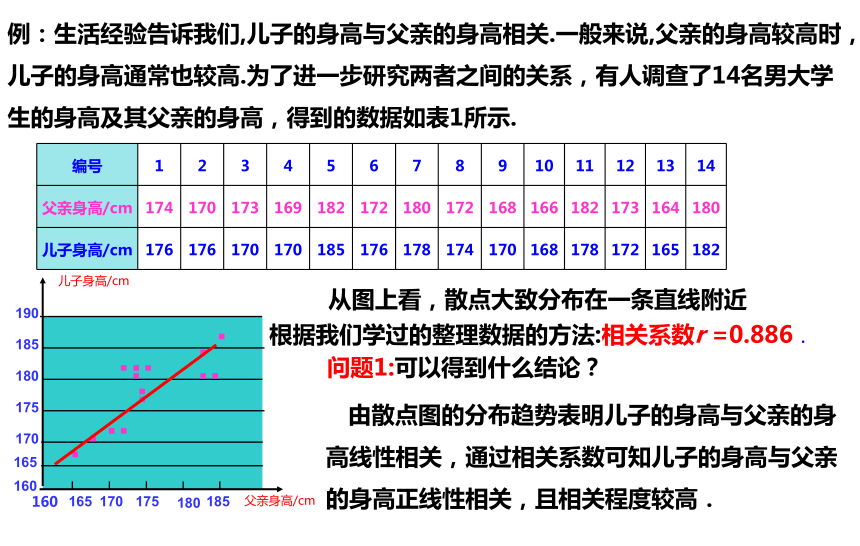
例:生活经验告诉我们,儿子的身高与父亲的身高相关.一般来说,父亲的身高较高时,儿子的身高通常也较高.为了进一步研究两者之间的关系,有人调查了14名男大学生的身高及其父亲的身高,得到的数据如表1所示.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
从图上看,散点大致分布在一条直线附近
根据我们学过的整理数据的方法:相关系数r =0.886.
父亲身高/cm
180
175
170
165
160
160
165
170
175
180
185
190
·
·
·
·
·
·
·
儿子身高/cm
·
·
·
·
·
·
·
185
问题1:可以得到什么结论?
由散点图的分布趋势表明儿子的身高与父亲的身高线性相关,通过相关系数可知儿子的身高与父亲的身高正线性相关,且相关程度较高.
问题3:那么影响儿子身高的其他因素是什么?
影响儿子身高的因素除父亲的身外,还有 母亲的身高、生活的环境、饮食习惯、营养水平、体育锻炼等随机的因素,儿子身高是父亲身高的函数的原因是存在这些随机的因素.
问题4: 各种随机因素都是独立的,有些因素又无法量化. 你能否考虑到这些随机因素的作用, 用类似于函数的表达式,表示儿子身高与父亲身高的关系吗
问题2:是否可以用函数模型来刻画?
不能,因为不符合函数的定义.这其中还受其它因素的影响.
如果用x表示父亲身高,Y表示儿子的身高,用e表示各种其它随机因素影响之和,称e为随机误差, 由于儿子身高与父亲身高线性相关,所以Y=bx+a.
考虑随机误差后,儿子的身高可以表示为:Y=bx+a+e
我们称①式为Y关于x的一元线性回归模型,其中,Y称为因变量或响应变量,x称为自变量或解释变量 . a称为截距参数,b称为斜率参数;e是Y与bx+a之间的随机误差.
①
一元线性回归模型
如果用x表示父亲身高,Y表示儿子的身高,e表示随机误差.假定随机误差e的均值为0,方差为与父亲身高无关的定值 ,则它们之间的关系可以表示为
由于随机误差表示大量已知和未知的各种影响之和,它们会相互抵消,为使问题简洁,可以假设随机误差e的均值为0,方差为与父亲身高无关的定值
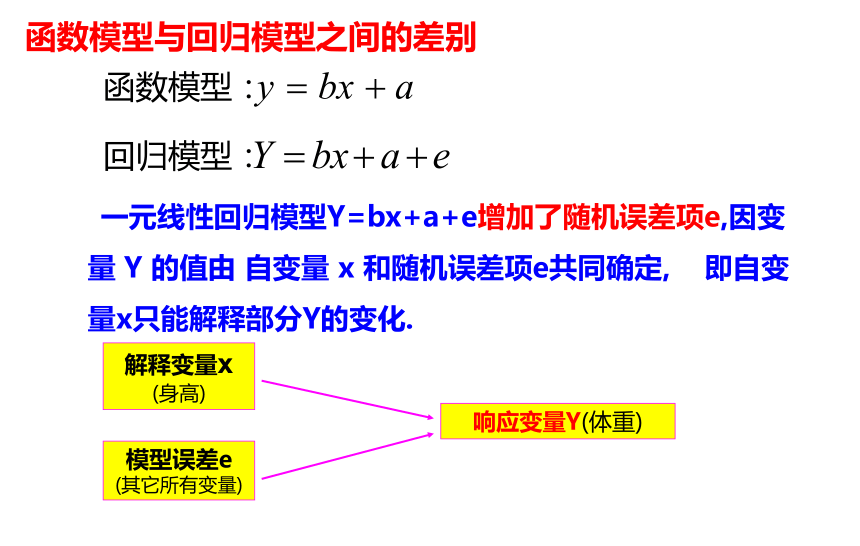
函数模型与回归模型之间的差别
函数模型:
回归模型:
一元线性回归模型Y=bx+a+e增加了随机误差项e,因变量 Y 的值由 自变量 x 和随机误差项e共同确定, 即自变量x只能解释部分Y的变化.
解释变量x (身高)
模型误差e (其它所有变量)
响应变量Y(体重)
问题5:你能结合父亲与儿子身高的实例,说明回归模型①的意义
①
可以解释为父亲身高为 的所有男大学生身高组成一个子总体,该子总体的均值为 ,即该子总体的均值与父亲的身高是线性函数关系.
而对于父亲身高为 的某一名男大学生,他的身高 并不一定为 ,它不仅是该子总体的一个观测值,这个观测值与均值有一个误差项 .
(1)除父亲身高外,其他可能影响儿子身高的因素,比如母亲身高、生活环境、饮食习惯和锻炼时间等.
(2)在测量儿子身高时,由于测量工具、测量精度所产生的测量误差.
(3)实际问题中,我们不知道儿子身高和父亲身高的相关 关系是什么,可以利用一元线性回归模型来近似这种关系,这种近似关系也是产生随机误差e的原因.
产生随机误差e的原因有:
问题6:你能结合具体实例解释产生模型①中随机误差项的原因吗
解: (1),(2),(3),(4),(5)回归模型(6),(7)函数模型.
巩固提升
判断下列变量间哪些能用函数模型刻画,哪些能用回归模型刻画 为什么?函数模型与回归模型有什么区别?
(1)某公司的销售收入和广告支出;
(2)某城市写字楼的出租率和每平米月租金;
(3)航空公司的顾客投诉次数和航班正点率;
(4)某地区的人均消费水平和人均国内生产总值(GDP);
(5)学生期末考试成绩和考前用于复习的时间;
(6)一辆汽车在某段路程中的行驶速度和行驶时间;
(7)正方形的面积与周长.
一元线性回归模型参数的最小二乘估计
在一元线性回归模型中,表达式 Y=bx+a+e刻画了变量Y与x之间的线性相关关系,其中参数a和b未知,那么我们如何来确定参数a和b的值呢?
问题:确定参数a和b的原则是什么?
与函数不同,回归模型的参数一般是无法精确求出的,只能通过成对样本数据估计这两个参数.
相当于寻找一条适当的直线,使表示成对样本数据的这些散点在整体上与这条直线最接近.
我们将 称为Y关于x的经验回归方程,也称经验回归函数或经验回归公式,其图形称为经验回归直线,这种求经验回归方程的方法叫最小二乘法.
1.对于一组具有线性相关关系的数据(x1 ,y1 ) ,(x2 , y2),···, (xn ,yn),
称为样本点的中心.经验回归直线必过点 .
练习:如果记录了x,y的几组数据分别为(0,1),(1,3),(2,5),(3,7),
那么y关于x的经验回归直线必过点( )
A.(2,2)
B.(1.5,2)
C.(1,2)
D.(1.5,4)
例2.某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:
x 6 8 10 12
y 2 3 5 6
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,建立y关于x的经验回归方程;
(3)预测记忆力为9的同学的判断力.
问题:当x=9时, ,记忆力为9的同学,他的判断力一定是4吗?为什么?
判断力不一定会是4,这是因为还有其他影响的因素判断力的因素,回归模型中的随机误差清楚地表达了这种影响, 不过,我们可以作出推测,当记忆力为9时,判断力一般在4左右.
参数b的含义:解释变量x对响应变量Y的均值的影响,变量x每增加一个单位,变量Y的均值将增加b个单位。
在使用经验回归方程进行预测时,需注意以下问题
1.回归方程只适用于我们所研究的样本的总体;
2.我们所建立的回归方程一般都有时间性;
3.样本采集的范围会影响回归方程的适用范围;
4.不能期望回归方程得到的预报值就是预报
变量的精确值.事实上,它是预报变量的可取
值的平均值.
建立经验回归方程后,通常需要对模型刻画数据的效果进行分析---残差分析
对于响应变量Y,通过观测得到的数据称为观测值,通过经验回归方程得到的数值称为预测值.观测值减去预测值称为残差.残差是随机误差的估计结果,通过对残差的分析可以判断模型刻画数据的效果,以及判断原始数据中是否存在可疑数据等,这方面的工作称为残差分析.
1.残差等于观测值减预测值;
2.残差的平方和越小越好;
3.原始数据中的可疑数据往往是残差绝对值过大的数据;
4.对数据刻画效果比较好的残差图特征:残差点比较均匀的集中在水平带状区域内.
【例】已知某成对样本数据的残差图如下,则样本点数据中可能不准确的是从左到右第( )个.
6
决定系数
(1)R2是用来刻画回归效果的,由R 2 =1- 可知R2越大,意味着残差平方和越小,也就是说模型的拟合效果越好.
(2)残差图也是用来刻画回归效果的,判断依据是:残差比较均匀地分布在横轴的两边,说明残差比较符合一元线性回归模型的假定.
判断模型拟合效果好坏的方法:
例:某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:
x 6 8 10 12
y 2 3 5 6
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,建立y关于x的经验回归方程;
(3)试根据求出的经验回归方程,预测记忆力为9的同学的判断力.
(4)列出残差表,做残差图
(5)求决定指数,说明拟合效果
(1)确定研究对象,明确哪个变量是解释变量,哪个变量是响应变量.
(2)画出解释变量与响应变量的散点图,观察它们之间的关系
(如是否存在线性关系等).
(3)由经验确定回归方程的类型.
(4)按一定规则(如最小二乘法)估计经验回归方程中的参数.
(5)得出结果后需进行线性回归分析.
①残差平方和越小,模型的拟合效果越好.
②决定系数R2取值越大,说明模型的拟合效果越好.
注意:若题中给出了检验回归方程是否理想的条件,
则根据题意进行分析检验即可.
建立线性回归模型的基本步骤
非线性经验回归方程
当经验回归方程并非形如y=bx+a(a,b∈R)时,称之为非线性经验回归方程,当两个变量不呈线性相关关系时,依据样本点的分布选择合适的曲线方程来模拟
x 1 2 3 4
y e e2 e3 e4
140 28 56 283
参考数据:
对于非线性经验回归问题,可以画出已知数据的散点图,把它与学过的各种函数(幂函数、对数函数、指数函数等)的图像作比较,挑选一种跟这些散点拟合得最好的函数,然后采用适当的变量变换,把非线性相关转化为线性相关,通过求经验回归方程来解决.
第八章
成对数据的统计分析
8.2一元线性回归模型及应用
通过前面的学习我们已经了解到,根据成对样本数据的散点图和样本相关系数,可以推断两个变量是否存在相关关系、是正相关还是负相关,以及线性相关程度的强弱等.
思考:是否能像建立函数模型刻画两个变量之间的确定性关系那样,通过建立适当的统计模型来刻画两变量之间的相关关系呢?
新课引入
例:生活经验告诉我们,儿子的身高与父亲的身高相关.一般来说,父亲的身高较高时,儿子的身高通常也较高.为了进一步研究两者之间的关系,有人调查了14名男大学生的身高及其父亲的身高,得到的数据如表1所示.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
从图上看,散点大致分布在一条直线附近
根据我们学过的整理数据的方法:相关系数r =0.886.
父亲身高/cm
180
175
170
165
160
160
165
170
175
180
185
190
·
·
·
·
·
·
·
儿子身高/cm
·
·
·
·
·
·
·
185
问题1:可以得到什么结论?
由散点图的分布趋势表明儿子的身高与父亲的身高线性相关,通过相关系数可知儿子的身高与父亲的身高正线性相关,且相关程度较高.
问题3:那么影响儿子身高的其他因素是什么?
影响儿子身高的因素除父亲的身外,还有 母亲的身高、生活的环境、饮食习惯、营养水平、体育锻炼等随机的因素,儿子身高是父亲身高的函数的原因是存在这些随机的因素.
问题4: 各种随机因素都是独立的,有些因素又无法量化. 你能否考虑到这些随机因素的作用, 用类似于函数的表达式,表示儿子身高与父亲身高的关系吗
问题2:是否可以用函数模型来刻画?
不能,因为不符合函数的定义.这其中还受其它因素的影响.
如果用x表示父亲身高,Y表示儿子的身高,用e表示各种其它随机因素影响之和,称e为随机误差, 由于儿子身高与父亲身高线性相关,所以Y=bx+a.
考虑随机误差后,儿子的身高可以表示为:Y=bx+a+e
我们称①式为Y关于x的一元线性回归模型,其中,Y称为因变量或响应变量,x称为自变量或解释变量 . a称为截距参数,b称为斜率参数;e是Y与bx+a之间的随机误差.
①
一元线性回归模型
如果用x表示父亲身高,Y表示儿子的身高,e表示随机误差.假定随机误差e的均值为0,方差为与父亲身高无关的定值 ,则它们之间的关系可以表示为
由于随机误差表示大量已知和未知的各种影响之和,它们会相互抵消,为使问题简洁,可以假设随机误差e的均值为0,方差为与父亲身高无关的定值
函数模型与回归模型之间的差别
函数模型:
回归模型:
一元线性回归模型Y=bx+a+e增加了随机误差项e,因变量 Y 的值由 自变量 x 和随机误差项e共同确定, 即自变量x只能解释部分Y的变化.
解释变量x (身高)
模型误差e (其它所有变量)
响应变量Y(体重)
问题5:你能结合父亲与儿子身高的实例,说明回归模型①的意义
①
可以解释为父亲身高为 的所有男大学生身高组成一个子总体,该子总体的均值为 ,即该子总体的均值与父亲的身高是线性函数关系.
而对于父亲身高为 的某一名男大学生,他的身高 并不一定为 ,它不仅是该子总体的一个观测值,这个观测值与均值有一个误差项 .
(1)除父亲身高外,其他可能影响儿子身高的因素,比如母亲身高、生活环境、饮食习惯和锻炼时间等.
(2)在测量儿子身高时,由于测量工具、测量精度所产生的测量误差.
(3)实际问题中,我们不知道儿子身高和父亲身高的相关 关系是什么,可以利用一元线性回归模型来近似这种关系,这种近似关系也是产生随机误差e的原因.
产生随机误差e的原因有:
问题6:你能结合具体实例解释产生模型①中随机误差项的原因吗
解: (1),(2),(3),(4),(5)回归模型(6),(7)函数模型.
巩固提升
判断下列变量间哪些能用函数模型刻画,哪些能用回归模型刻画 为什么?函数模型与回归模型有什么区别?
(1)某公司的销售收入和广告支出;
(2)某城市写字楼的出租率和每平米月租金;
(3)航空公司的顾客投诉次数和航班正点率;
(4)某地区的人均消费水平和人均国内生产总值(GDP);
(5)学生期末考试成绩和考前用于复习的时间;
(6)一辆汽车在某段路程中的行驶速度和行驶时间;
(7)正方形的面积与周长.
一元线性回归模型参数的最小二乘估计
在一元线性回归模型中,表达式 Y=bx+a+e刻画了变量Y与x之间的线性相关关系,其中参数a和b未知,那么我们如何来确定参数a和b的值呢?
问题:确定参数a和b的原则是什么?
与函数不同,回归模型的参数一般是无法精确求出的,只能通过成对样本数据估计这两个参数.
相当于寻找一条适当的直线,使表示成对样本数据的这些散点在整体上与这条直线最接近.
我们将 称为Y关于x的经验回归方程,也称经验回归函数或经验回归公式,其图形称为经验回归直线,这种求经验回归方程的方法叫最小二乘法.
1.对于一组具有线性相关关系的数据(x1 ,y1 ) ,(x2 , y2),···, (xn ,yn),
称为样本点的中心.经验回归直线必过点 .
练习:如果记录了x,y的几组数据分别为(0,1),(1,3),(2,5),(3,7),
那么y关于x的经验回归直线必过点( )
A.(2,2)
B.(1.5,2)
C.(1,2)
D.(1.5,4)
例2.某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:
x 6 8 10 12
y 2 3 5 6
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,建立y关于x的经验回归方程;
(3)预测记忆力为9的同学的判断力.
问题:当x=9时, ,记忆力为9的同学,他的判断力一定是4吗?为什么?
判断力不一定会是4,这是因为还有其他影响的因素判断力的因素,回归模型中的随机误差清楚地表达了这种影响, 不过,我们可以作出推测,当记忆力为9时,判断力一般在4左右.
参数b的含义:解释变量x对响应变量Y的均值的影响,变量x每增加一个单位,变量Y的均值将增加b个单位。
在使用经验回归方程进行预测时,需注意以下问题
1.回归方程只适用于我们所研究的样本的总体;
2.我们所建立的回归方程一般都有时间性;
3.样本采集的范围会影响回归方程的适用范围;
4.不能期望回归方程得到的预报值就是预报
变量的精确值.事实上,它是预报变量的可取
值的平均值.
建立经验回归方程后,通常需要对模型刻画数据的效果进行分析---残差分析
对于响应变量Y,通过观测得到的数据称为观测值,通过经验回归方程得到的数值称为预测值.观测值减去预测值称为残差.残差是随机误差的估计结果,通过对残差的分析可以判断模型刻画数据的效果,以及判断原始数据中是否存在可疑数据等,这方面的工作称为残差分析.
1.残差等于观测值减预测值;
2.残差的平方和越小越好;
3.原始数据中的可疑数据往往是残差绝对值过大的数据;
4.对数据刻画效果比较好的残差图特征:残差点比较均匀的集中在水平带状区域内.
【例】已知某成对样本数据的残差图如下,则样本点数据中可能不准确的是从左到右第( )个.
6
决定系数
(1)R2是用来刻画回归效果的,由R 2 =1- 可知R2越大,意味着残差平方和越小,也就是说模型的拟合效果越好.
(2)残差图也是用来刻画回归效果的,判断依据是:残差比较均匀地分布在横轴的两边,说明残差比较符合一元线性回归模型的假定.
判断模型拟合效果好坏的方法:
例:某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:
x 6 8 10 12
y 2 3 5 6
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,建立y关于x的经验回归方程;
(3)试根据求出的经验回归方程,预测记忆力为9的同学的判断力.
(4)列出残差表,做残差图
(5)求决定指数,说明拟合效果
(1)确定研究对象,明确哪个变量是解释变量,哪个变量是响应变量.
(2)画出解释变量与响应变量的散点图,观察它们之间的关系
(如是否存在线性关系等).
(3)由经验确定回归方程的类型.
(4)按一定规则(如最小二乘法)估计经验回归方程中的参数.
(5)得出结果后需进行线性回归分析.
①残差平方和越小,模型的拟合效果越好.
②决定系数R2取值越大,说明模型的拟合效果越好.
注意:若题中给出了检验回归方程是否理想的条件,
则根据题意进行分析检验即可.
建立线性回归模型的基本步骤
非线性经验回归方程
当经验回归方程并非形如y=bx+a(a,b∈R)时,称之为非线性经验回归方程,当两个变量不呈线性相关关系时,依据样本点的分布选择合适的曲线方程来模拟
x 1 2 3 4
y e e2 e3 e4
140 28 56 283
参考数据:
对于非线性经验回归问题,可以画出已知数据的散点图,把它与学过的各种函数(幂函数、对数函数、指数函数等)的图像作比较,挑选一种跟这些散点拟合得最好的函数,然后采用适当的变量变换,把非线性相关转化为线性相关,通过求经验回归方程来解决.
