第30章二次函数单元复习题2023-2024学年冀教版九年级数学下册(含解析)
文档属性
| 名称 | 第30章二次函数单元复习题2023-2024学年冀教版九年级数学下册(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 518.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-29 00:00:00 | ||
图片预览



文档简介
冀教版九年级数学下册第30章二次函数单元复习题
一、单选题
1.二次函数的最小值是( )
A. B. C. D.
2.将二次函数的图象向上平移3个单位长度,得到新的二次函数的表达式为( )
A. B.
C. D.
3.如果将抛物线y=x2+4x+1平移,使它与抛物线y=x2+1重合,那么平移的方式可以是( )
A.向左平移2个单位,向上平移4个单位
B.向左平移2个单位,向下平移4个单位
C.向右平移2个单位,向上平移4个单位
D.向右平移2个单位,向下平移4个单位
4.二次函数y=﹣(x﹣3)2+1的最大值为( )
A.1 B.﹣1 C.3 D.﹣3
5.已知烟花弹爆炸后某个残片的空中飞行轨迹可以看成为二次函数图象的一部分,其中x为爆炸后经过的时间(秒),y为残片离地面的高度(米),请问在爆炸后1秒到6秒之间,残片距离地面的高度范围为( )
A.0米到3米 B.5米到8米 C.到8米 D.5米到米
6.已知二次函数 的图像如图所示,那么 、 、 的符号为( )
A. B.
C. D.
7.抛物线y=ax2+bx+c的顶点坐标是(-1,3),且过点(0,5),那么二次函数y=ax2+bx+c的解析式为( )
A.y=-2x2+4x+5 B.y=2x2+4x+5
C.y=-2x2+4x-1 D.y=2x2+4x+3
8.关于x的一元二次方程x2﹣x﹣n=0没有实数根,则抛物线y=x2﹣x﹣n的顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落到点C’处;作∠BPC’的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A. B.
C. D.
10.如图,二次函数 图象的一部分与x轴的一个交点坐标为 ,对称轴为 ,结合图象给出下列结论:
① ;
② ;
③关于x的一元二次方程 的两根分别为-3和1;
④若点 , , 均在二次函数图象上,则 ;
⑤ (m为任意实数).
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.已知y=2x2﹣3x+1,当x=1时,函数值为 .
12.利用二次函数的图象求一元二次方程x2+2x﹣10=0的根:
(1)
x ﹣4.1 ﹣4.2 ﹣4.3 ﹣4.4
y ﹣1.39 ﹣0.76 ﹣0.11 0.56
是方程的一个近似根.
(2)
x 2.1 2.2 2.3 2.4
y ﹣1.39 ﹣0.76 ﹣0.11 0.56
是方程的另一个近似根.
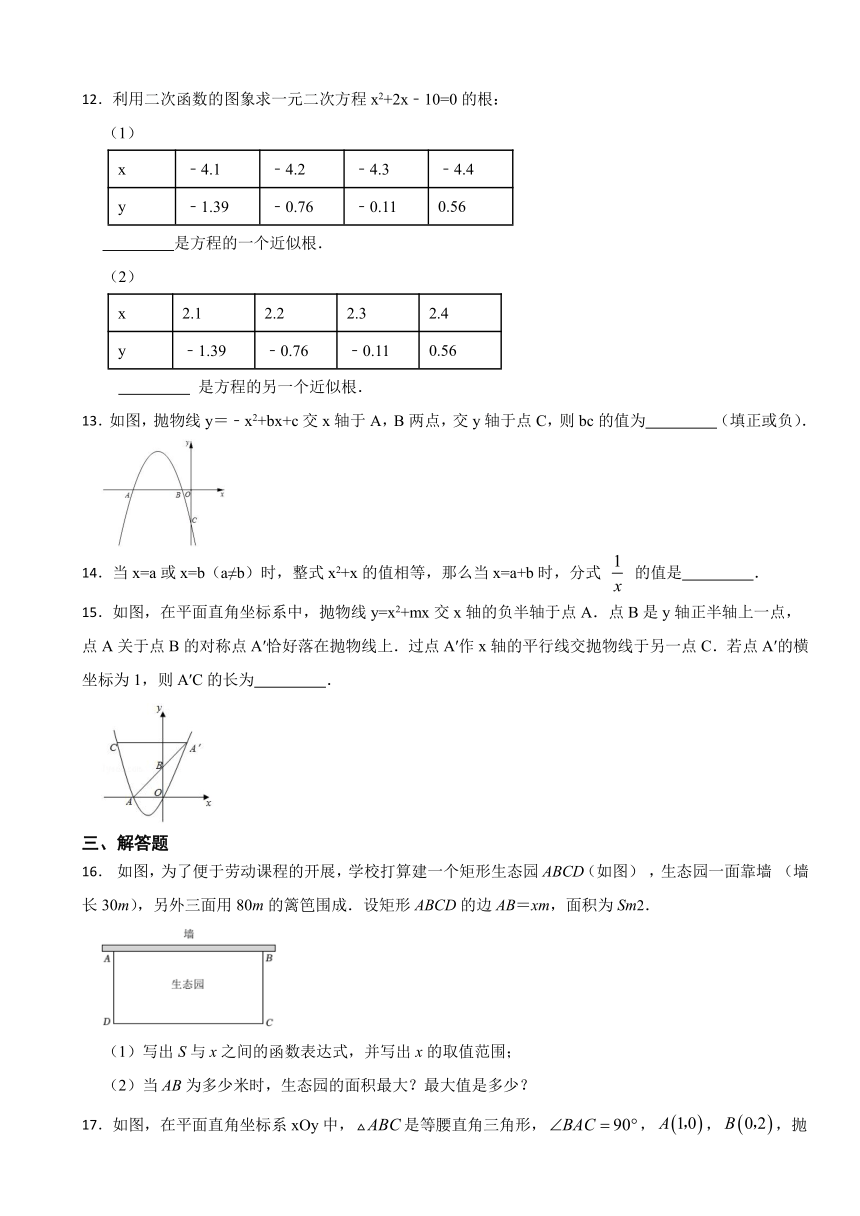
13.如图,抛物线y=﹣x2+bx+c交x轴于A,B两点,交y轴于点C,则bc的值为 (填正或负).
14.当x=a或x=b(a≠b)时,整式x2+x的值相等,那么当x=a+b时,分式 的值是 .
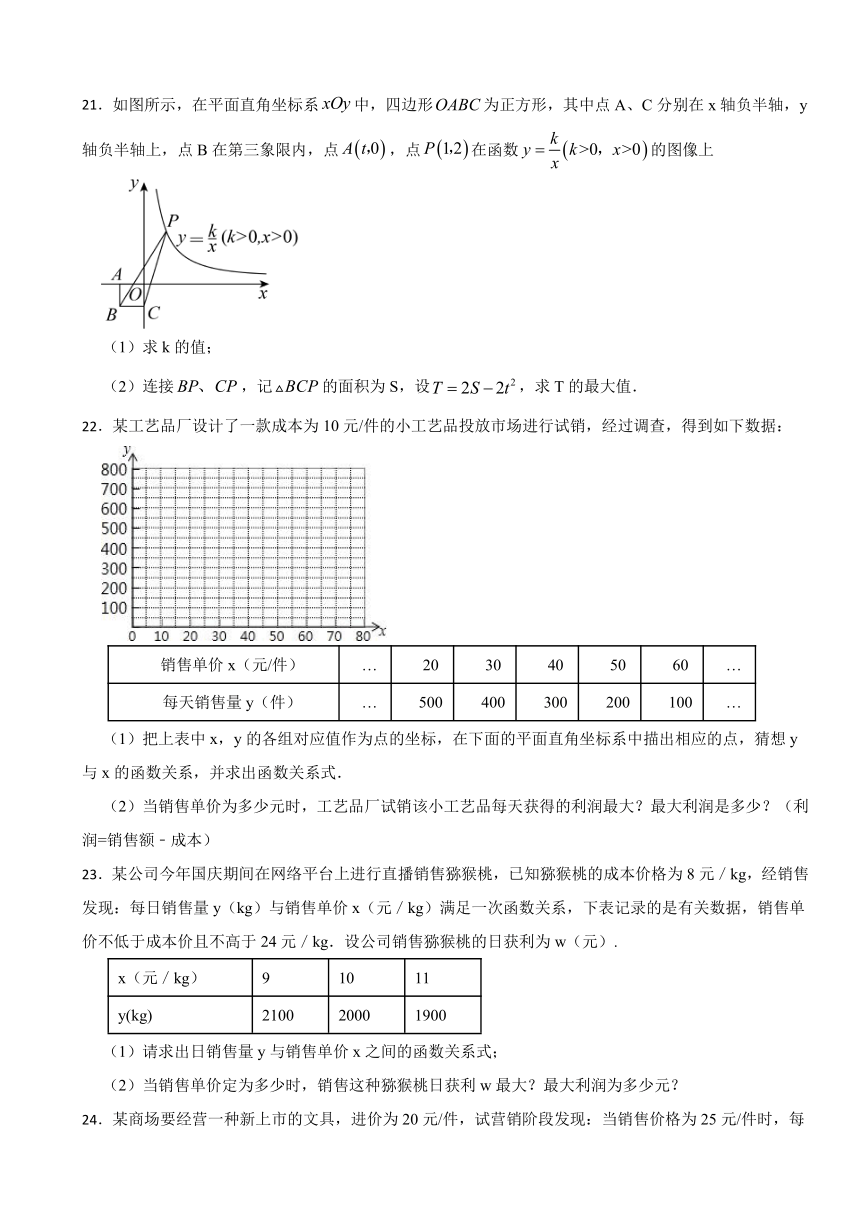
15.如图,在平面直角坐标系中,抛物线y=x2+mx交x轴的负半轴于点A.点B是y轴正半轴上一点,点A关于点B的对称点A′恰好落在抛物线上.过点A′作x轴的平行线交抛物线于另一点C.若点A′的横坐标为1,则A′C的长为 .
三、解答题
16. 如图,为了便于劳动课程的开展,学校打算建一个矩形生态园ABCD(如图) ,生态园一面靠墙 (墙长30m),另外三面用80m的篱笆围成.设矩形ABCD的边AB=xm,面积为Sm2.
(1)写出S与x之间的函数表达式,并写出x的取值范围;
(2)当AB为多少米时,生态园的面积最大?最大值是多少?
17.如图,在平面直角坐标系xOy中,是等腰直角三角形,,,,抛物线过点C.求抛物线的表达式.
18.已知二次函数y=x2+bx+c的图象经过点A(-1,-10),B(2,8)两点.
(1)求b,c的值.
(2)求该函数图象与x轴的交点坐标.
19.如图,四边形ABCD是边长为2,一个锐角等于60°的菱形纸片,小芳同学将一个三角形纸片的一个顶点与该菱形顶点D重合,按顺时针方向旋转三角形纸片,使它的两边分别交CB、BA(或它们的延长线)于点E、F,∠EDF=60°,当CE=AF时,如图1小芳同学得出的结论是DE=DF.
(1)继续旋转三角形纸片,当CE≠AF时,如图2小芳的结论是否成立?若成立,加以证明;若不成立,请说明理由;
(2)再次旋转三角形纸片,当点E、F分别在CB、BA的延长线上时,如图3请直接写出DE与DF的数量关系;
(3)连EF,若△DEF的面积为y,CE=x,求y与x的关系式,并指出当x为何值时,y有最小值,最小值是多少?
20.已知:如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.过点C作CD∥x轴,交抛物线的对称轴于点D.
(1)求该抛物线的解析式;
(2)若将该抛物线向下平移m个单位,使其顶点落在D点,求m的值.
四、综合题
21.如图所示,在平面直角坐标系中,四边形为正方形,其中点A、C分别在x轴负半轴,y轴负半轴上,点B在第三象限内,点,点在函数的图像上
(1)求k的值;
(2)连接,记的面积为S,设,求T的最大值.
22.某工艺品厂设计了一款成本为10元/件的小工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价x(元/件) … 20 30 40 50 60 …
每天销售量y(件) … 500 400 300 200 100 …
(1)把上表中x,y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式.
(2)当销售单价为多少元时,工艺品厂试销该小工艺品每天获得的利润最大?最大利润是多少?(利润=销售额﹣成本)
23.某公司今年国庆期间在网络平台上进行直播销售猕猴桃,已知猕猴桃的成本价格为8元/kg,经销售发现:每日销售量y(kg)与销售单价x(元/kg)满足一次函数关系,下表记录的是有关数据,销售单价不低于成本价且不高于24元/kg.设公司销售猕猴桃的日获利为w(元).
x(元/kg) 9 10 11
y(kg) 2100 2000 1900
(1)请求出日销售量y与销售单价x之间的函数关系式;
(2)当销售单价定为多少时,销售这种猕猴桃日获利w最大?最大利润为多少元?
24.某商场要经营一种新上市的文具,进价为20元/件,试营销阶段发现:当销售价格为25元/件时,每天的销售量为250件,每件销售价格每上涨1元,每天的销售量就减少10件.
(1)当销售价格上涨时,请写出每天的销售量 (件)与销售价格(元/件)之间的函数关系式.
(2)如果要求每天的销售量不少于10件,且每件文具的利润至少为18元,间当销售价格定为多少时,该文具每天的销售利润最大,最大利润为多少?
25.某公司营销A、B两种产品,根据市场调研,发现如下信息:
信息1:销售A种产品所获利润y(万元)与销售产品x(吨)之间存在二次函数关系y=ax2+bx.在x=1时,y=1.4;当x=3时,y=3.6.
信息2:销售B种产品所获利润y(万元)与销售产品x(吨)之间存在正比例函数关系y=0.3x.
根据以上信息,解答下列问题;
(1)求二次函数解析式;
(2)该公司准备购进A、B两种产品共10吨,请设计一个营销方案,使销售A、B两种产品获得的利润之和最大,最大利润是多少?
26.如图,点 是边长为 的正方形 对角线上一个动点( 与 不重合),以 为圆心, 长为半径画圆弧,交线段 于点 ,联结 ,与 交于点 .设 的长为 , 的面积为 .
(1)判断 的形状,并说明理由;
(2)求 与 之间的函数关系式,并写出定义域;
(3)当四边形 是梯形时,求出 的值.
答案解析部分
1.【答案】B
【解析】【解答】解:二次函数y=(x-2)2+3,
当x=2时,最小值是3,
故答案为:B.
【分析】根据二次函数的性质解答即可.
2.【答案】A
【解析】【解答】解:二次函数的图象向上平移3个单位长度后得到的解析式为:.
故答案为:A.
【分析】根据函数解析式平移的特征:左加右减,上加下减求解即可。
3.【答案】C
【解析】【解答】解:由题知,抛物线y=x2+4x+1=(x+2)2-3,再根据“左加右减”,知图像向右平移2个单位,向上平移4个单位,可与抛物线y=x2+1重合.
所以答案选:C。
【分析】分别找出两抛物线的顶点坐标,然后根据点的坐标与平移的规律:“横坐标左减右加,纵坐标上加下减”即可得出平移的方向及距离,从而即可得出答案。
4.【答案】A
【解析】【解答】∵ ,∴此函数的顶点坐标是(3,1),即当x=3时,函数有最大值1.故答案为:A.
【分析】由题意a=-1<0,抛物线的开口向下,则图像有最高点,即函数有最大值,根据二次函数的性质可得,当x=3时,函数有最大值1。
5.【答案】B
【解析】【解答】解:∵,
∴当 时, ,即此时残片离地面的高度最大,最大为8米,
∵ ,
∴在直线 的左侧,y随x的增大而增大;在直线 的右侧,y随x的增大而减小,
∵当 时, ,当 时, ,且 ,
∴在爆炸后1秒到6秒之间,残片距离地面的高度范围为5米到8米.
故答案为:B.
【分析】先把抛物线解析式化为顶点式,根据顶点坐标得出此时残片离地面的最大高度,再讨论二次函数的增减趋势,结合始末点的高度,即可求解.
6.【答案】B
【解析】【解答】∵抛物线开口向下,
∴a<0,
∵抛物线与y轴的正半轴相交,
∴c>0,
∵ ,
∴b<0,
故答案为:B.
【分析】根据开口方向可判断a,根据与y轴的交点可判断c,根据对称轴可判断B.
7.【答案】B
【解析】【分析】由顶点坐标是(-1,3)可设函数关系式为y=a(x+1)2+3,再把(0,5)代入即可求得函数关系式,最后化为一般式即可。
【解答】由题意函数关系式为y=a(x+1)2+3
∵图象过点(0,5)
∴a+3=5,则a=2
∴函数关系式为y=2(x+1)2+3=2x2+4x=5
故选B.
【点评】本题属于基础应用题,只需学生熟练掌握待定系数法求函数关系式,即可完成。
8.【答案】A
【解析】【解答】解:∵抛物线y=x2﹣x﹣n的对称轴x=﹣=,
∴可知抛物线的顶点在y轴的右侧,
又∵关于x的一元二次方程x2﹣x﹣n=0没有实数根,
∴开口向上的y=x2﹣x﹣n与x轴没有交点,
∴抛物线y=x2﹣x﹣n的顶点在第一象限.
故选A.
【分析】求出抛物线y=x2﹣x﹣n的对称轴x=,可知顶点在y轴的右侧,根据x2﹣x﹣n=0在实数范围内没有实数根,可知开口向上的y=x2﹣x﹣n与x轴没有交点,据此即可判断抛物线在第一象限.
9.【答案】D
【解析】【解答】解:∵△PC′D是△PCD沿PD折叠得到,
∴∠CPD=∠C′PD,
∵PE平分∠BPC′,
∴∠BPE=∠C′PE,
∴∠BPE+∠CPD=×180°=90°,
又∵∠BPE+∠BEP=90°,
∴∠CPD=∠BEP,
又∵∠B=∠C,
∴△BEP~△CPD,
∴,
∵BP=x,BE=y,CD=AB=3,BC=5,
∴CP=BC-BP=5-x,
∴
所以y=x2+x(0<x<5),
纵观各选项,只有D选项符合.
故选:D.
【分析】判定△BEP~△CPD,则代入相应的值,即可求出x,y之间的关系.
10.【答案】C
【解析】【解答】解:∵二次函数 图象的一部分与x轴的一个交点坐标为 ,
∴当x=1时, ,
故结论①符合题意;
根据函数图象可知,
当 ,即 ,
对称轴为 ,即 ,
根据抛物线开口向上,得 ,
∴ ,
∴ ,
即 ,
故结论②符合题意;
根据抛物线与x轴的一个交点为 ,
对称轴为 可知:抛物线与x轴的另一个交点为(-3,0),
∴关于x的一元二次方程 的两根分别为-3和1,
故结论③符合题意;
根据函数图象可知: ,
故结论④不符合题意;
当 时, ,
∴当 时, ,
即 ,
故结论⑤不符合题意,
综上:①②③符合题意,
故答案为:C.
【分析】根据二次函数 图象的一部分与x轴的一个交点坐标为 ,对称轴为 ,再结合函数图象对每个结论一一判断求解即可。
11.【答案】0
【解析】【解答】解:y=2x2-3x+1,
当x=1时,y=2×12-3×1+1=0.
故答案为:0.
【分析】将x=1代入函数解析式,进行计算,可求出对应的y的值.
12.【答案】﹣4.32;2.32
【解析】【解答】解:如图:
x=﹣4.3,y=﹣0.11;x=﹣4.4,y=0.56,x2+2x﹣10=0的一个近似根是﹣4.32;
x=2.3,y=﹣0.11,x=2.4,y=0.56x2+2x﹣10=0的一个近似根是2.32.
故答案为:﹣4.32,2.32.
【分析】根据函数图象,及函数值,可得一元二次方程的近似根.
13.【答案】正
【解析】【解答】解:由图可知,抛物线的开口方向向下,则a<0,
抛物线的对称轴位于y轴的左侧,则a、b同号,即b<0,
抛物线与y轴交于负半轴,则c<0,
所以bc>0,即bc的值为正,
故答案为:正.
【分析】根据抛物线的开口方向判定a<0,根据对称轴位于y轴左侧判定a、b同号,根据抛物线与y轴交点位置判定c的符号,最后即可求解。
14.【答案】-1
【解析】【解答】解:∵当x=a或x=b(a≠b)时,整式x2+x的值相等,
∴a2+a=b2+b,
∴(a﹣b)(a+b+1)=0,
∵a﹣b≠0,
∴a+b+1=0,
∴a+b=﹣1,
∴x=a+b时, = =﹣1,
故答案为﹣1.
【分析】根据题意得a2+a=b2+b,整理得出a+b=1,再代入即可.
15.【答案】3
【解析】【解答】解: 当y=0时,x2+mx=0,解得x1=0,x2=﹣m,则A(﹣m,0),
∵点A关于点B的对称点为A′,点A′的横坐标为1,
∴点A的坐标为(﹣1,0),
∴抛物线解析式为y=x2+x,
当x=1时,y=x2+x=2,则A′(1,2),
当y=2时,x2+x=2,解得x1=﹣2,x2=1,则C(﹣2,2),
∴A′C的长为1﹣(﹣2)=3.
故答案为:3.
【分析】因为 抛物线y=x2+mx交x轴的负半轴于点A ,所以可得方程x2+mx=0,解方程可得x1=0,x2=﹣m,则A(﹣m,0);而点A关于点B的对称点为A′,点A′的横坐标为1,所以可得点A的坐标为(﹣1,0),把点A的坐标(﹣1,0)代入解析式可求得m的值;则点 A′的纵坐标可求解;由题意可知点A′和点C是抛物线上的一对对称点,由轴对称的性质即可求得点C的横坐标,则 A′C的长=这两点的横坐标之差的绝对值。
16.【答案】(1)解:∵AB=xm,
∴AD=(80﹣x)m,
∴S=x(80﹣x),
∴S=﹣x2+40x,
∵墙长30m,
∴0<x≤30,
∴S与x之间的函数关系式为S=﹣x2+40x,自变量x的取值范围为0<x≤30;
(2)解:由(1)知,S=﹣x2+40x=﹣(x﹣40)2+800,
∵﹣<8,0<x≤30,
∴当x=30时,y有最大值.
答:当AB为30米时,生态园的面积最大,最大值为750平方米.
【解析】【分析】(1) 设矩形ABCD的边AB=xm ,根据 生态园一面靠墙 (墙长30m),另外三面用80m的篱笆围成,面积为Sm2,,利用矩形的面积公式代入数据即可求解;
(2)根据(1)可得面积与自变量x的二次函数关系式,利用二次函数的性质即可求出最大面积与此时的AB的长.
17.【答案】解:过点C作轴于点D,则,即,
∵是等腰直角三角形,
∴,,
∴,
∴, 又,
∴,
∴,,
∵,,
∴,,
∴,,
∴点C的坐标为,
∵点在抛物线上,
∴,解得,
∴抛物线的表达式为.
【解析】【分析】过点C作轴于点D,则,先证明求出,,再求出点C的坐标,最后将点C的坐标代入求出b的值即可。
18.【答案】(1)解:点A(-1,-10),B(2,8)代入抛物线 y=x2+bx+c ,得
∴;
(2)解:∵b=5,c=-6,
∴y=x2+5x-6,
令y=0,解得:x1=1,x2=-6,
∴二次函数与x轴的交点坐标为(1,0),(-6,0).
【解析】【分析】(1)依据题意,将A、B代入解析式y=x2+bx+c,可得关于字母b、c的方程组,求解可得b、c的值;
(2)由(1)再令y=0,从而计算可以得解.
19.【答案】(1)解:DF=DE.理由如下:
如图1,连接BD.
∵四边形ABCD是菱形,
∴AD=AB.
又∵∠A=60°,
∴△ABD是等边三角形,
∴AD=BD,∠ADB=60°,
∴∠DBE=∠A=60°
∵∠EDF=60°,
∴∠ADF=∠BDE.∵在△ADF与△BDE中,
,
∴△ADF≌△BDE(ASA),
∴DF=DE;
(2)解:DF=DE.理由如下:
如图2,连接BD.
∵四边形ABCD是菱形,
∴AD=AB.
又∵∠A=60°,
∴△ABD是等边三角形,
∴AD=BD,∠ADB=60°,
∴∠DBE=∠A=60°
∵∠EDF=60°,
∴∠ADF=∠BDE.
∵在△ADF与△BDE中,
,
∴△ADF≌△BDE(ASA),
∴DF=DE;
(3)解:由(2)知,△ADF≌△BDE.则S△ADF=S△BDE,AF=BE=x.
依题意得:y=S△BEF+S△ABD= (2+x)xsin60°+ ×2×2sin60°= (x+1)2+ .
即y= (x+1)2+ .
∵ >0,
∴该抛物线的开口方向向上,
∴当x=0即点E、B重合时,y最小值=
【解析】【分析】(1)连接BD,根据菱形的性质可以判断三角形ABD为等边三角形,根据三角形全等判定定理,两个角及其夹边相等的三角形全等,可以证明△ADF≌△BDE(ASA),继而得出DF=DE。
(2)根据菱形的性质可以判断三角形ABD为等边三角形,根据三角形全等判定定理,两个角及其夹边相等的三角形全等,可以证明△ADF≌△BDE(ASA),继而得出DF=DE。
(3)根据三角形面积的计算公式,将△BEF和△ABD的面积表示出来,根据二次函数求出面积的最小值即可。
20.【答案】解:(1)将A(﹣1,0),B(3,0)代入y=﹣x2+bx+c中,
得:,
解得:.
则抛物线解析式为y=﹣x2+2x+3;
(2)当x=0,y=3,即OC=3,
∵抛物线解析式为y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点坐标为(1,4),
∵对称轴为直线,
∴CD=1,
∵CD∥x轴,
∴D(1,3),
∴m=4﹣3=1.
【解析】【分析】(1)利用待定系数法即可求得解析式;
(2)根据抛物线的解析式先求得C的坐标,然后把抛物线的解析式转化成顶点式,求得抛物线的顶点,即可求得D的坐标,从而求得m的值.
21.【答案】(1)解:∵点在函数的图像上,
∴,
∴,
即k的值为2;
(2)解:∵点在x轴负半轴,
∴,
∵四边形为正方形,
∴,轴,
∴的面积为,
∴,
∵,
∴抛物线开口向下,
∴当时,有最大值,T的最大值是1.
【解析】【分析】(1)运用待定系数法求反比例函数将点P代入即可求解;
(2)先根据题意得到,再根据正方形的性质结合三角形的面积公式即可得到,进而得到T,再根据二次函数的最值即可求解。
22.【答案】(1)解:画出图形,如右图所示.
由图可猜想y与x是一次函数关系,设这个一次函数为y=kx+b(k≠0),
∵这个一次函数的图象经过(20,500),(30,400)两点,
∴ ,解得: ,
∴函数关系式是y=﹣10x+700.
经验证,其他各点也在y=﹣10x+700上
(2)解:设工艺品试销每天获得利润为W元,
由已知得:W=(x﹣10)(﹣10x+700)=﹣10x2+800x﹣7000=﹣10(x﹣40)2+9000,
∵﹣10<0,
∴当x=40时,W取最大值,最大值为9000.
故:当销售单价为40元时,工艺品厂试销该小工艺品每天获得的利润最大,最大利润是9000元.
【解析】【分析】(1)将表中各点描在坐标系中,根据点的分别可猜想y与x是一次函数关系,设这个一次函数为y=kx+b(k≠0),根据点的坐标利用待定系数法即可求出该函数关系式式,再验证其余各点是否在该函数关系式的图象上,由此即可得出结论;(2)设工艺品试销每天获得利润为W元,根据“利用=单件利润×销售数量”即可得出W关于x的函数关系式,利用配方法结合二次函数的性质即可解决最值问题.
23.【答案】(1)解:设y=kx+b
则
∴
∴
(2)解:由题意得:
∴对称轴为x=19
∵,a=-100<0
∴当x=19,即 销售单价定为19时,销售这种猕猴桃日获利w最大,最大利润为12100元.
【解析】【分析】(1)由待定系数法,得出结果。
(2)由二次函数配方法,得出,从而得出结果。
24.【答案】(1)解:
∴每天的销售量 (件)与销售价格 (元/件)之间的函数关系式为:
(2)解:设销售利润为 元,由题意得:
∵ ,解得:
∵ ,抛物线的对称轴为直线
∴抛物线开口向下,在对称轴的右侧, 随 的增大而减小
∴当 时, 取最大值为2160.
答:当销售价格定为38元时,该文具每天的销售利润最大,最大利润为2160元.
【解析】【分析】(1)根据实际销售量等于250减去10(x 25),化简即可;
(2)设销售利润为w元,由题意得关于x的二次函数,利用二次函数的性质及题中对销售量及每件文具利润的约束条件,可求得答案.
25.【答案】(1)解:∵当x=1时,y=1.4;当x=3时,y=3.6,
∴ ,
解得 ,
所以,二次函数解析式为y=﹣0.1x2+1.5x
(2)解:设购进A产品m吨,购进B产品(10﹣m)吨,销售A、B两种产品获得的利润之和为W元,
则W=﹣0.1m2+1.5m+0.3(10﹣m)=﹣0.1m2+1.2m+3=﹣0.1(m﹣6)2+6.6,
∵﹣0.1<0,
∴当m=6时,W有最大值6.6,
∴购进A产品6吨,购进B产品4吨,销售A、B两种产品获得的利润之和最大,最大利润是6.6万元
【解析】【分析】(1)把两组数据代入二次函数解析式,然后利用待定系数法求解即可;(2)设购进A产品m吨,购进B产品(10﹣m)吨,销售A、B两种产品获得的利润之和为W元,根据总利润等于两种产品的利润的和列式整理得到W与m的函数关系式,再根据二次函数的最值问题解答.
26.【答案】(1)解: 为等腰直角三角形,理由如下:
在正方形 中, ,
又 ,
由题意可得, ,
过点 作 ,与 分别交于点 ,
在正方形 中,
四边形 是矩形,
在 中,
又
为等腰直角三角形
(2)解: 在 中, ,
在 中,
为等腰直角三角形,
(3)解:在等腰直角三角形 中,
,
当四边形 是梯形时,只有可能 ,
【解析】【分析】(1)先证明 ,再证明四边形 是矩形,再证明 ,可得 , 即可得 为等腰直角三角形.(2)由 , ,即可求得 与 之间的函数关系式.(3)因为四边形 是梯形时,得 .求PF的长,需利用已知条件求AC,AP,CE的长,则 即可得出答案.
一、单选题
1.二次函数的最小值是( )
A. B. C. D.
2.将二次函数的图象向上平移3个单位长度,得到新的二次函数的表达式为( )
A. B.
C. D.
3.如果将抛物线y=x2+4x+1平移,使它与抛物线y=x2+1重合,那么平移的方式可以是( )
A.向左平移2个单位,向上平移4个单位
B.向左平移2个单位,向下平移4个单位
C.向右平移2个单位,向上平移4个单位
D.向右平移2个单位,向下平移4个单位
4.二次函数y=﹣(x﹣3)2+1的最大值为( )
A.1 B.﹣1 C.3 D.﹣3
5.已知烟花弹爆炸后某个残片的空中飞行轨迹可以看成为二次函数图象的一部分,其中x为爆炸后经过的时间(秒),y为残片离地面的高度(米),请问在爆炸后1秒到6秒之间,残片距离地面的高度范围为( )
A.0米到3米 B.5米到8米 C.到8米 D.5米到米
6.已知二次函数 的图像如图所示,那么 、 、 的符号为( )
A. B.
C. D.
7.抛物线y=ax2+bx+c的顶点坐标是(-1,3),且过点(0,5),那么二次函数y=ax2+bx+c的解析式为( )
A.y=-2x2+4x+5 B.y=2x2+4x+5
C.y=-2x2+4x-1 D.y=2x2+4x+3
8.关于x的一元二次方程x2﹣x﹣n=0没有实数根,则抛物线y=x2﹣x﹣n的顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落到点C’处;作∠BPC’的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A. B.
C. D.
10.如图,二次函数 图象的一部分与x轴的一个交点坐标为 ,对称轴为 ,结合图象给出下列结论:
① ;
② ;
③关于x的一元二次方程 的两根分别为-3和1;
④若点 , , 均在二次函数图象上,则 ;
⑤ (m为任意实数).
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.已知y=2x2﹣3x+1,当x=1时,函数值为 .
12.利用二次函数的图象求一元二次方程x2+2x﹣10=0的根:
(1)
x ﹣4.1 ﹣4.2 ﹣4.3 ﹣4.4
y ﹣1.39 ﹣0.76 ﹣0.11 0.56
是方程的一个近似根.
(2)
x 2.1 2.2 2.3 2.4
y ﹣1.39 ﹣0.76 ﹣0.11 0.56
是方程的另一个近似根.
13.如图,抛物线y=﹣x2+bx+c交x轴于A,B两点,交y轴于点C,则bc的值为 (填正或负).
14.当x=a或x=b(a≠b)时,整式x2+x的值相等,那么当x=a+b时,分式 的值是 .
15.如图,在平面直角坐标系中,抛物线y=x2+mx交x轴的负半轴于点A.点B是y轴正半轴上一点,点A关于点B的对称点A′恰好落在抛物线上.过点A′作x轴的平行线交抛物线于另一点C.若点A′的横坐标为1,则A′C的长为 .
三、解答题
16. 如图,为了便于劳动课程的开展,学校打算建一个矩形生态园ABCD(如图) ,生态园一面靠墙 (墙长30m),另外三面用80m的篱笆围成.设矩形ABCD的边AB=xm,面积为Sm2.
(1)写出S与x之间的函数表达式,并写出x的取值范围;
(2)当AB为多少米时,生态园的面积最大?最大值是多少?
17.如图,在平面直角坐标系xOy中,是等腰直角三角形,,,,抛物线过点C.求抛物线的表达式.
18.已知二次函数y=x2+bx+c的图象经过点A(-1,-10),B(2,8)两点.
(1)求b,c的值.
(2)求该函数图象与x轴的交点坐标.
19.如图,四边形ABCD是边长为2,一个锐角等于60°的菱形纸片,小芳同学将一个三角形纸片的一个顶点与该菱形顶点D重合,按顺时针方向旋转三角形纸片,使它的两边分别交CB、BA(或它们的延长线)于点E、F,∠EDF=60°,当CE=AF时,如图1小芳同学得出的结论是DE=DF.
(1)继续旋转三角形纸片,当CE≠AF时,如图2小芳的结论是否成立?若成立,加以证明;若不成立,请说明理由;
(2)再次旋转三角形纸片,当点E、F分别在CB、BA的延长线上时,如图3请直接写出DE与DF的数量关系;
(3)连EF,若△DEF的面积为y,CE=x,求y与x的关系式,并指出当x为何值时,y有最小值,最小值是多少?
20.已知:如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.过点C作CD∥x轴,交抛物线的对称轴于点D.
(1)求该抛物线的解析式;
(2)若将该抛物线向下平移m个单位,使其顶点落在D点,求m的值.
四、综合题
21.如图所示,在平面直角坐标系中,四边形为正方形,其中点A、C分别在x轴负半轴,y轴负半轴上,点B在第三象限内,点,点在函数的图像上
(1)求k的值;
(2)连接,记的面积为S,设,求T的最大值.
22.某工艺品厂设计了一款成本为10元/件的小工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价x(元/件) … 20 30 40 50 60 …
每天销售量y(件) … 500 400 300 200 100 …
(1)把上表中x,y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式.
(2)当销售单价为多少元时,工艺品厂试销该小工艺品每天获得的利润最大?最大利润是多少?(利润=销售额﹣成本)
23.某公司今年国庆期间在网络平台上进行直播销售猕猴桃,已知猕猴桃的成本价格为8元/kg,经销售发现:每日销售量y(kg)与销售单价x(元/kg)满足一次函数关系,下表记录的是有关数据,销售单价不低于成本价且不高于24元/kg.设公司销售猕猴桃的日获利为w(元).
x(元/kg) 9 10 11
y(kg) 2100 2000 1900
(1)请求出日销售量y与销售单价x之间的函数关系式;
(2)当销售单价定为多少时,销售这种猕猴桃日获利w最大?最大利润为多少元?
24.某商场要经营一种新上市的文具,进价为20元/件,试营销阶段发现:当销售价格为25元/件时,每天的销售量为250件,每件销售价格每上涨1元,每天的销售量就减少10件.
(1)当销售价格上涨时,请写出每天的销售量 (件)与销售价格(元/件)之间的函数关系式.
(2)如果要求每天的销售量不少于10件,且每件文具的利润至少为18元,间当销售价格定为多少时,该文具每天的销售利润最大,最大利润为多少?
25.某公司营销A、B两种产品,根据市场调研,发现如下信息:
信息1:销售A种产品所获利润y(万元)与销售产品x(吨)之间存在二次函数关系y=ax2+bx.在x=1时,y=1.4;当x=3时,y=3.6.
信息2:销售B种产品所获利润y(万元)与销售产品x(吨)之间存在正比例函数关系y=0.3x.
根据以上信息,解答下列问题;
(1)求二次函数解析式;
(2)该公司准备购进A、B两种产品共10吨,请设计一个营销方案,使销售A、B两种产品获得的利润之和最大,最大利润是多少?
26.如图,点 是边长为 的正方形 对角线上一个动点( 与 不重合),以 为圆心, 长为半径画圆弧,交线段 于点 ,联结 ,与 交于点 .设 的长为 , 的面积为 .
(1)判断 的形状,并说明理由;
(2)求 与 之间的函数关系式,并写出定义域;
(3)当四边形 是梯形时,求出 的值.
答案解析部分
1.【答案】B
【解析】【解答】解:二次函数y=(x-2)2+3,
当x=2时,最小值是3,
故答案为:B.
【分析】根据二次函数的性质解答即可.
2.【答案】A
【解析】【解答】解:二次函数的图象向上平移3个单位长度后得到的解析式为:.
故答案为:A.
【分析】根据函数解析式平移的特征:左加右减,上加下减求解即可。
3.【答案】C
【解析】【解答】解:由题知,抛物线y=x2+4x+1=(x+2)2-3,再根据“左加右减”,知图像向右平移2个单位,向上平移4个单位,可与抛物线y=x2+1重合.
所以答案选:C。
【分析】分别找出两抛物线的顶点坐标,然后根据点的坐标与平移的规律:“横坐标左减右加,纵坐标上加下减”即可得出平移的方向及距离,从而即可得出答案。
4.【答案】A
【解析】【解答】∵ ,∴此函数的顶点坐标是(3,1),即当x=3时,函数有最大值1.故答案为:A.
【分析】由题意a=-1<0,抛物线的开口向下,则图像有最高点,即函数有最大值,根据二次函数的性质可得,当x=3时,函数有最大值1。
5.【答案】B
【解析】【解答】解:∵,
∴当 时, ,即此时残片离地面的高度最大,最大为8米,
∵ ,
∴在直线 的左侧,y随x的增大而增大;在直线 的右侧,y随x的增大而减小,
∵当 时, ,当 时, ,且 ,
∴在爆炸后1秒到6秒之间,残片距离地面的高度范围为5米到8米.
故答案为:B.
【分析】先把抛物线解析式化为顶点式,根据顶点坐标得出此时残片离地面的最大高度,再讨论二次函数的增减趋势,结合始末点的高度,即可求解.
6.【答案】B
【解析】【解答】∵抛物线开口向下,
∴a<0,
∵抛物线与y轴的正半轴相交,
∴c>0,
∵ ,
∴b<0,
故答案为:B.
【分析】根据开口方向可判断a,根据与y轴的交点可判断c,根据对称轴可判断B.
7.【答案】B
【解析】【分析】由顶点坐标是(-1,3)可设函数关系式为y=a(x+1)2+3,再把(0,5)代入即可求得函数关系式,最后化为一般式即可。
【解答】由题意函数关系式为y=a(x+1)2+3
∵图象过点(0,5)
∴a+3=5,则a=2
∴函数关系式为y=2(x+1)2+3=2x2+4x=5
故选B.
【点评】本题属于基础应用题,只需学生熟练掌握待定系数法求函数关系式,即可完成。
8.【答案】A
【解析】【解答】解:∵抛物线y=x2﹣x﹣n的对称轴x=﹣=,
∴可知抛物线的顶点在y轴的右侧,
又∵关于x的一元二次方程x2﹣x﹣n=0没有实数根,
∴开口向上的y=x2﹣x﹣n与x轴没有交点,
∴抛物线y=x2﹣x﹣n的顶点在第一象限.
故选A.
【分析】求出抛物线y=x2﹣x﹣n的对称轴x=,可知顶点在y轴的右侧,根据x2﹣x﹣n=0在实数范围内没有实数根,可知开口向上的y=x2﹣x﹣n与x轴没有交点,据此即可判断抛物线在第一象限.
9.【答案】D
【解析】【解答】解:∵△PC′D是△PCD沿PD折叠得到,
∴∠CPD=∠C′PD,
∵PE平分∠BPC′,
∴∠BPE=∠C′PE,
∴∠BPE+∠CPD=×180°=90°,
又∵∠BPE+∠BEP=90°,
∴∠CPD=∠BEP,
又∵∠B=∠C,
∴△BEP~△CPD,
∴,
∵BP=x,BE=y,CD=AB=3,BC=5,
∴CP=BC-BP=5-x,
∴
所以y=x2+x(0<x<5),
纵观各选项,只有D选项符合.
故选:D.
【分析】判定△BEP~△CPD,则代入相应的值,即可求出x,y之间的关系.
10.【答案】C
【解析】【解答】解:∵二次函数 图象的一部分与x轴的一个交点坐标为 ,
∴当x=1时, ,
故结论①符合题意;
根据函数图象可知,
当 ,即 ,
对称轴为 ,即 ,
根据抛物线开口向上,得 ,
∴ ,
∴ ,
即 ,
故结论②符合题意;
根据抛物线与x轴的一个交点为 ,
对称轴为 可知:抛物线与x轴的另一个交点为(-3,0),
∴关于x的一元二次方程 的两根分别为-3和1,
故结论③符合题意;
根据函数图象可知: ,
故结论④不符合题意;
当 时, ,
∴当 时, ,
即 ,
故结论⑤不符合题意,
综上:①②③符合题意,
故答案为:C.
【分析】根据二次函数 图象的一部分与x轴的一个交点坐标为 ,对称轴为 ,再结合函数图象对每个结论一一判断求解即可。
11.【答案】0
【解析】【解答】解:y=2x2-3x+1,
当x=1时,y=2×12-3×1+1=0.
故答案为:0.
【分析】将x=1代入函数解析式,进行计算,可求出对应的y的值.
12.【答案】﹣4.32;2.32
【解析】【解答】解:如图:
x=﹣4.3,y=﹣0.11;x=﹣4.4,y=0.56,x2+2x﹣10=0的一个近似根是﹣4.32;
x=2.3,y=﹣0.11,x=2.4,y=0.56x2+2x﹣10=0的一个近似根是2.32.
故答案为:﹣4.32,2.32.
【分析】根据函数图象,及函数值,可得一元二次方程的近似根.
13.【答案】正
【解析】【解答】解:由图可知,抛物线的开口方向向下,则a<0,
抛物线的对称轴位于y轴的左侧,则a、b同号,即b<0,
抛物线与y轴交于负半轴,则c<0,
所以bc>0,即bc的值为正,
故答案为:正.
【分析】根据抛物线的开口方向判定a<0,根据对称轴位于y轴左侧判定a、b同号,根据抛物线与y轴交点位置判定c的符号,最后即可求解。
14.【答案】-1
【解析】【解答】解:∵当x=a或x=b(a≠b)时,整式x2+x的值相等,
∴a2+a=b2+b,
∴(a﹣b)(a+b+1)=0,
∵a﹣b≠0,
∴a+b+1=0,
∴a+b=﹣1,
∴x=a+b时, = =﹣1,
故答案为﹣1.
【分析】根据题意得a2+a=b2+b,整理得出a+b=1,再代入即可.
15.【答案】3
【解析】【解答】解: 当y=0时,x2+mx=0,解得x1=0,x2=﹣m,则A(﹣m,0),
∵点A关于点B的对称点为A′,点A′的横坐标为1,
∴点A的坐标为(﹣1,0),
∴抛物线解析式为y=x2+x,
当x=1时,y=x2+x=2,则A′(1,2),
当y=2时,x2+x=2,解得x1=﹣2,x2=1,则C(﹣2,2),
∴A′C的长为1﹣(﹣2)=3.
故答案为:3.
【分析】因为 抛物线y=x2+mx交x轴的负半轴于点A ,所以可得方程x2+mx=0,解方程可得x1=0,x2=﹣m,则A(﹣m,0);而点A关于点B的对称点为A′,点A′的横坐标为1,所以可得点A的坐标为(﹣1,0),把点A的坐标(﹣1,0)代入解析式可求得m的值;则点 A′的纵坐标可求解;由题意可知点A′和点C是抛物线上的一对对称点,由轴对称的性质即可求得点C的横坐标,则 A′C的长=这两点的横坐标之差的绝对值。
16.【答案】(1)解:∵AB=xm,
∴AD=(80﹣x)m,
∴S=x(80﹣x),
∴S=﹣x2+40x,
∵墙长30m,
∴0<x≤30,
∴S与x之间的函数关系式为S=﹣x2+40x,自变量x的取值范围为0<x≤30;
(2)解:由(1)知,S=﹣x2+40x=﹣(x﹣40)2+800,
∵﹣<8,0<x≤30,
∴当x=30时,y有最大值.
答:当AB为30米时,生态园的面积最大,最大值为750平方米.
【解析】【分析】(1) 设矩形ABCD的边AB=xm ,根据 生态园一面靠墙 (墙长30m),另外三面用80m的篱笆围成,面积为Sm2,,利用矩形的面积公式代入数据即可求解;
(2)根据(1)可得面积与自变量x的二次函数关系式,利用二次函数的性质即可求出最大面积与此时的AB的长.
17.【答案】解:过点C作轴于点D,则,即,
∵是等腰直角三角形,
∴,,
∴,
∴, 又,
∴,
∴,,
∵,,
∴,,
∴,,
∴点C的坐标为,
∵点在抛物线上,
∴,解得,
∴抛物线的表达式为.
【解析】【分析】过点C作轴于点D,则,先证明求出,,再求出点C的坐标,最后将点C的坐标代入求出b的值即可。
18.【答案】(1)解:点A(-1,-10),B(2,8)代入抛物线 y=x2+bx+c ,得
∴;
(2)解:∵b=5,c=-6,
∴y=x2+5x-6,
令y=0,解得:x1=1,x2=-6,
∴二次函数与x轴的交点坐标为(1,0),(-6,0).
【解析】【分析】(1)依据题意,将A、B代入解析式y=x2+bx+c,可得关于字母b、c的方程组,求解可得b、c的值;
(2)由(1)再令y=0,从而计算可以得解.
19.【答案】(1)解:DF=DE.理由如下:
如图1,连接BD.
∵四边形ABCD是菱形,
∴AD=AB.
又∵∠A=60°,
∴△ABD是等边三角形,
∴AD=BD,∠ADB=60°,
∴∠DBE=∠A=60°
∵∠EDF=60°,
∴∠ADF=∠BDE.∵在△ADF与△BDE中,
,
∴△ADF≌△BDE(ASA),
∴DF=DE;
(2)解:DF=DE.理由如下:
如图2,连接BD.
∵四边形ABCD是菱形,
∴AD=AB.
又∵∠A=60°,
∴△ABD是等边三角形,
∴AD=BD,∠ADB=60°,
∴∠DBE=∠A=60°
∵∠EDF=60°,
∴∠ADF=∠BDE.
∵在△ADF与△BDE中,
,
∴△ADF≌△BDE(ASA),
∴DF=DE;
(3)解:由(2)知,△ADF≌△BDE.则S△ADF=S△BDE,AF=BE=x.
依题意得:y=S△BEF+S△ABD= (2+x)xsin60°+ ×2×2sin60°= (x+1)2+ .
即y= (x+1)2+ .
∵ >0,
∴该抛物线的开口方向向上,
∴当x=0即点E、B重合时,y最小值=
【解析】【分析】(1)连接BD,根据菱形的性质可以判断三角形ABD为等边三角形,根据三角形全等判定定理,两个角及其夹边相等的三角形全等,可以证明△ADF≌△BDE(ASA),继而得出DF=DE。
(2)根据菱形的性质可以判断三角形ABD为等边三角形,根据三角形全等判定定理,两个角及其夹边相等的三角形全等,可以证明△ADF≌△BDE(ASA),继而得出DF=DE。
(3)根据三角形面积的计算公式,将△BEF和△ABD的面积表示出来,根据二次函数求出面积的最小值即可。
20.【答案】解:(1)将A(﹣1,0),B(3,0)代入y=﹣x2+bx+c中,
得:,
解得:.
则抛物线解析式为y=﹣x2+2x+3;
(2)当x=0,y=3,即OC=3,
∵抛物线解析式为y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点坐标为(1,4),
∵对称轴为直线,
∴CD=1,
∵CD∥x轴,
∴D(1,3),
∴m=4﹣3=1.
【解析】【分析】(1)利用待定系数法即可求得解析式;
(2)根据抛物线的解析式先求得C的坐标,然后把抛物线的解析式转化成顶点式,求得抛物线的顶点,即可求得D的坐标,从而求得m的值.
21.【答案】(1)解:∵点在函数的图像上,
∴,
∴,
即k的值为2;
(2)解:∵点在x轴负半轴,
∴,
∵四边形为正方形,
∴,轴,
∴的面积为,
∴,
∵,
∴抛物线开口向下,
∴当时,有最大值,T的最大值是1.
【解析】【分析】(1)运用待定系数法求反比例函数将点P代入即可求解;
(2)先根据题意得到,再根据正方形的性质结合三角形的面积公式即可得到,进而得到T,再根据二次函数的最值即可求解。
22.【答案】(1)解:画出图形,如右图所示.
由图可猜想y与x是一次函数关系,设这个一次函数为y=kx+b(k≠0),
∵这个一次函数的图象经过(20,500),(30,400)两点,
∴ ,解得: ,
∴函数关系式是y=﹣10x+700.
经验证,其他各点也在y=﹣10x+700上
(2)解:设工艺品试销每天获得利润为W元,
由已知得:W=(x﹣10)(﹣10x+700)=﹣10x2+800x﹣7000=﹣10(x﹣40)2+9000,
∵﹣10<0,
∴当x=40时,W取最大值,最大值为9000.
故:当销售单价为40元时,工艺品厂试销该小工艺品每天获得的利润最大,最大利润是9000元.
【解析】【分析】(1)将表中各点描在坐标系中,根据点的分别可猜想y与x是一次函数关系,设这个一次函数为y=kx+b(k≠0),根据点的坐标利用待定系数法即可求出该函数关系式式,再验证其余各点是否在该函数关系式的图象上,由此即可得出结论;(2)设工艺品试销每天获得利润为W元,根据“利用=单件利润×销售数量”即可得出W关于x的函数关系式,利用配方法结合二次函数的性质即可解决最值问题.
23.【答案】(1)解:设y=kx+b
则
∴
∴
(2)解:由题意得:
∴对称轴为x=19
∵,a=-100<0
∴当x=19,即 销售单价定为19时,销售这种猕猴桃日获利w最大,最大利润为12100元.
【解析】【分析】(1)由待定系数法,得出结果。
(2)由二次函数配方法,得出,从而得出结果。
24.【答案】(1)解:
∴每天的销售量 (件)与销售价格 (元/件)之间的函数关系式为:
(2)解:设销售利润为 元,由题意得:
∵ ,解得:
∵ ,抛物线的对称轴为直线
∴抛物线开口向下,在对称轴的右侧, 随 的增大而减小
∴当 时, 取最大值为2160.
答:当销售价格定为38元时,该文具每天的销售利润最大,最大利润为2160元.
【解析】【分析】(1)根据实际销售量等于250减去10(x 25),化简即可;
(2)设销售利润为w元,由题意得关于x的二次函数,利用二次函数的性质及题中对销售量及每件文具利润的约束条件,可求得答案.
25.【答案】(1)解:∵当x=1时,y=1.4;当x=3时,y=3.6,
∴ ,
解得 ,
所以,二次函数解析式为y=﹣0.1x2+1.5x
(2)解:设购进A产品m吨,购进B产品(10﹣m)吨,销售A、B两种产品获得的利润之和为W元,
则W=﹣0.1m2+1.5m+0.3(10﹣m)=﹣0.1m2+1.2m+3=﹣0.1(m﹣6)2+6.6,
∵﹣0.1<0,
∴当m=6时,W有最大值6.6,
∴购进A产品6吨,购进B产品4吨,销售A、B两种产品获得的利润之和最大,最大利润是6.6万元
【解析】【分析】(1)把两组数据代入二次函数解析式,然后利用待定系数法求解即可;(2)设购进A产品m吨,购进B产品(10﹣m)吨,销售A、B两种产品获得的利润之和为W元,根据总利润等于两种产品的利润的和列式整理得到W与m的函数关系式,再根据二次函数的最值问题解答.
26.【答案】(1)解: 为等腰直角三角形,理由如下:
在正方形 中, ,
又 ,
由题意可得, ,
过点 作 ,与 分别交于点 ,
在正方形 中,
四边形 是矩形,
在 中,
又
为等腰直角三角形
(2)解: 在 中, ,
在 中,
为等腰直角三角形,
(3)解:在等腰直角三角形 中,
,
当四边形 是梯形时,只有可能 ,
【解析】【分析】(1)先证明 ,再证明四边形 是矩形,再证明 ,可得 , 即可得 为等腰直角三角形.(2)由 , ,即可求得 与 之间的函数关系式.(3)因为四边形 是梯形时,得 .求PF的长,需利用已知条件求AC,AP,CE的长,则 即可得出答案.
