(预习衔接讲义)第四单元第11课时比例的应用(知识精讲+典题精练)-2023-2024学年六年级下册数学高频易错尖子生培优(人教版)(含解析)
文档属性
| 名称 | (预习衔接讲义)第四单元第11课时比例的应用(知识精讲+典题精练)-2023-2024学年六年级下册数学高频易错尖子生培优(人教版)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 187.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-27 16:52:23 | ||
图片预览




文档简介
第四单元第11课时比例的应用
1.比的意义
【知识点归纳】
两个数相除,也叫两个数的比.
2.比例的应用
【知识点归纳】
根据问题中的不变量找出两种相关联的量,并判断这两种相关联的量成什么比例关系,根据正、反比例关系式列出相应的方程并求解.
3.图形的放大与缩小
【知识点归纳】
1.图形的放大和缩小是生活中常见的现象,把一个图形放大或缩小后所得到的图形与元图形相比,形状相同,大小不同.
2.方法:一看、二算、三画.
4.比例尺
【知识点归纳】
1.比例尺:
表示图上距离比实地距离缩小的程度,因此也叫缩尺.图上距离和实际距离的比,叫做这幅图的比例尺.
即:图上距离:实际距离=图上距离÷比例尺
比例尺分类:
比例尺一般分为数值比例尺和线段比例尺:
(1)数值比例尺:例如一幅图的比例尺是1:20000或.为了方便,通常把比例尺写成前项(或后项)是1的比.
(2)线段比例尺是在图上附上一条标有数量的线段,用来表示实际相对应的距离.
2.比例尺表示方法:
用公式表示为:实际距离=图上距离÷比例尺.比例尺通常有三种表示方法.
(1)数字式,用数字的比例式或分数式表示比例尺的大小.例如地图上1厘米代表实地距离500千米,可写成:1:50000000或写成:.
(2)线段式,在地图上画一条线段,并注明地图上1厘米所代表的实际距离.
(3)文字式,在地图上用文字直接写出地图上1厘米代表实地距离多少千米,如:图上1厘米相当于地面距离500千米,或五千万分之一.
3.比例尺公式:
图上距离=实际距离×比例尺
实际距离=图上距离÷比例尺
比例尺=图上距离÷实际距离.
一.选择题(共8小题)
1.阳光小区新建一个长方形健身广场,长100m、宽60m。王叔叔把它画在规格是“30cm×21cm”的图纸上,他应选择哪个比例尺比较合适?( )
A.1:500 B.1:200 C.1000:1 D.1:5000
2.把线段比例尺改成数值比例尺是( )
A.1:30 B.1:90 C.1:3000000 D.1:9000000
3.漳平与华安两地相距48千米,在一幅地图上,量得漳平与华安的图上距离是6厘米,这幅地图的比例尺是( )
A.1:600000 B.1:80000 C.1:800000 D.1:8000000
4.将如图所示的线段比例尺,改写成数值比例尺是( )
A.1:2000000 B.1:4000000 C.1:600000
5.甲、乙两地相距20km,画在设计图纸上的长度是5cm,图纸的比例尺是( )
A.1:400000 B.400000:1 C.1:4 D.4:1
6.一块长方形的试验田,长180米,宽60米,如果把它画成平面示意图,画在一张作业纸上,选用( )比例尺比较合适。
A.1:200 B.1:2000 C.1:20000 D.1:200000
7.如图,把三角形ABC按2:1的比放大,三角形ABC放大前、后相对应的“三角形的面积”、“∠1的度数”、“AB与BC的比值”三个要素中,不变化的有( )个。
A.1 B.2 C.3
8.把一张长方形照片按6:1的比例放大,照片长与宽的比是( )
A.不变 B.变了 C.6;1 D.1:6
二.填空题(共7小题)
9.一个2mm长的精密零件画到图纸上长4cm,那么这幅图的比例尺是( )。如果这幅图纸上有一个零件长6cm,那么这个零件的实际长度是 mm。
10.把如图比例尺改写成数值比例尺是 ;如果实际距离是210km,那么图上距离是 cm。
11.小莉的身高是1.5m,妈妈的身高是160cm,旅游时她和妈妈拍了一张照片,照片上小莉的身高是3cm,这张照片的比例尺是 ,小莉和妈妈实际的身高之比是 。
12.在一幅地图上,用2.5厘米的长度表示实际距离20千米,这幅地图的比例尺是 .
13.如图,欢欢沿着直尺的方向拉橡皮筋。如果点A的位置固定不变,将橡皮筋继续拉长,使点C的位置在16厘米处,那么点B的位置在 厘米处;如果使点B的位置在15厘米处,那么点C的位置在 厘米处。
14.如图是一个线段比例尺,改成数值比例尺是 。测得图上宁波到杭州的
距离是3.1厘米,实际距离是 千米。
15.甲地到乙地的实际距离是500km,在比例尺是1:20000000的地图上,甲、乙两地之间的长度是 厘米.
三.判断题(共9小题)
16.一幅地图的比例尺是,把它改写成数值比例尺是1:2400000. (判断对错)
17.把长与宽的比是3:1的长方形按2:1放大后,新长方形的长和宽的比是6:1。 (判断对错)
18.在比例中,图上距离1cm表示实际距离160km (判断对错)
19.把一个长方形按边长1:3的比例缩小后,周长会比原来缩小3倍,面积会比原来缩小6倍。 (判断对错)
20.在比例尺是1:16000000的地图上,图上1cm表示实际的160km。 (判断对错)
21.在一幅平面图上,图上距离是3厘米,实际距离是6米,这幅图的比例尺是1:2. .(判断对错)
22.一幅地图中某两地的图上距离5cm表示实际距离15km,这幅图的比例尺是1:300000。 (判断对错)
23.图形按比放大时,要使放大前后图形对应线段的比相等。 (判断对错)
24.一个零件长3mm,画在图纸上长4.5cm,这幅图的比例尺是1:15。 (判断对错)
四.计算题(共2小题)
25.将图1的三角形按比例缩小后得到图2的三角形,求未知数x.
26.先计算再填表.
图上距离 实际距离 比例尺
3厘米 1:50000
2.5厘米 50千米
180千米 1:12000000
五.操作题(共1小题)
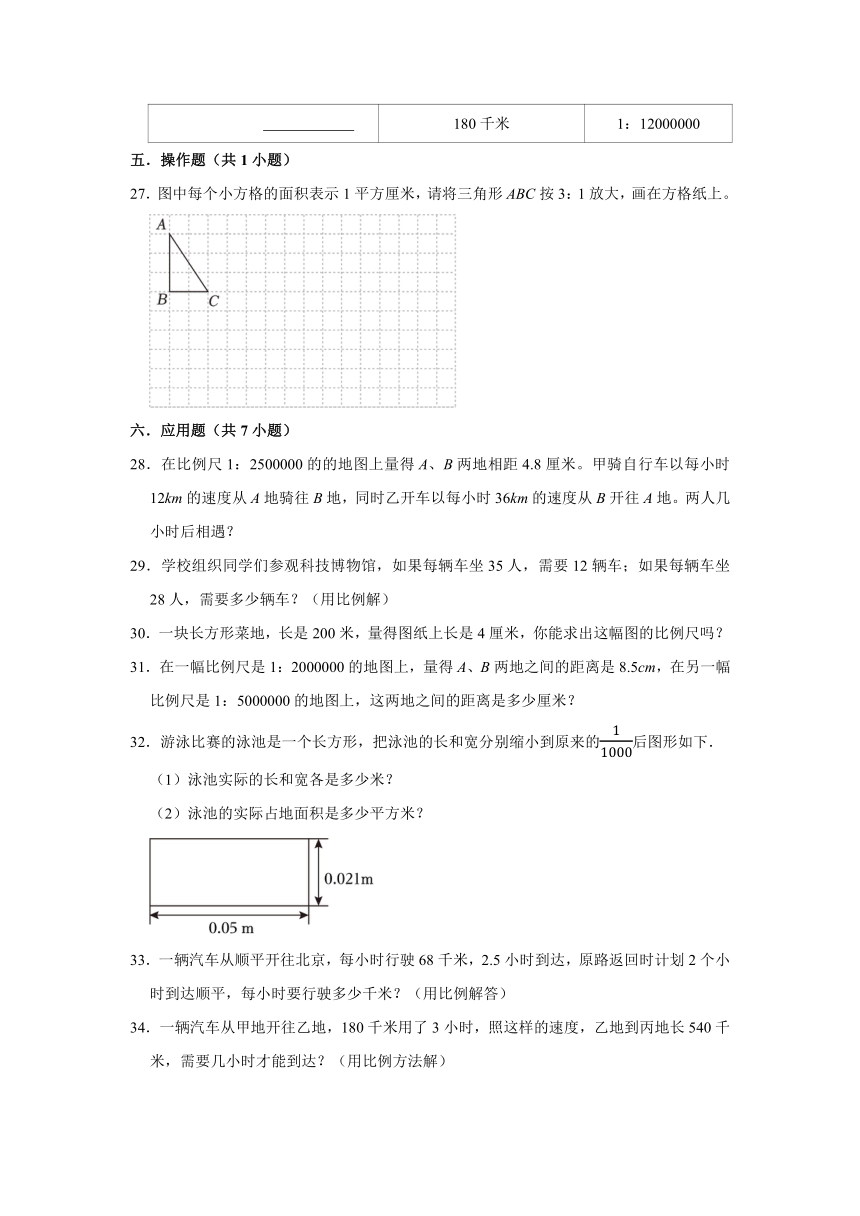
27.图中每个小方格的面积表示1平方厘米,请将三角形ABC按3:1放大,画在方格纸上。
六.应用题(共7小题)
28.在比例尺1:2500000的的地图上量得A、B两地相距4.8厘米。甲骑自行车以每小时12km的速度从A地骑往B地,同时乙开车以每小时36km的速度从B开往A地。两人几小时后相遇?
29.学校组织同学们参观科技博物馆,如果每辆车坐35人,需要12辆车;如果每辆车坐28人,需要多少辆车?(用比例解)
30.一块长方形菜地,长是200米,量得图纸上长是4厘米,你能求出这幅图的比例尺吗?
31.在一幅比例尺是1:2000000的地图上,量得A、B两地之间的距离是8.5cm,在另一幅比例尺是1:5000000的地图上,这两地之间的距离是多少厘米?
32.游泳比赛的泳池是一个长方形,把泳池的长和宽分别缩小到原来的后图形如下.
(1)泳池实际的长和宽各是多少米?
(2)泳池的实际占地面积是多少平方米?
33.一辆汽车从顺平开往北京,每小时行驶68千米,2.5小时到达,原路返回时计划2个小时到达顺平,每小时要行驶多少千米?(用比例解答)
34.一辆汽车从甲地开往乙地,180千米用了3小时,照这样的速度,乙地到丙地长540千米,需要几小时才能到达?(用比例方法解)
第四单元第11课时比例的应用
参考答案与试题解析
一.选择题(共8小题)
1.【答案】A
【分析】根据图上距离=实际距离×比例尺计算出各选项的图上距离,再结合规格是“30cm×21cm”的图纸解答即可。
【解答】解:100米=10000厘米,60米=6000厘米
A.1000020(厘米)
600012(厘米)
画在规格是“30cm×21cm”的图纸上合适;
B.1000050(厘米)
600030(厘米)
把它画在规格是“30cm×21cm”的图纸上偏大,不合适;
C.1000010000000(厘米)
60006000000(厘米)
把它画在规格是“30cm×21cm”的图纸上太大,不合适;
D.100002(厘米)
60001.2(厘米)
把它画在规格是“30cm×21cm”的图纸上偏小。
故选:A。
【点评】本题考查了实际距离、图上距离、比例尺三者间的关系。
2.【答案】C
【分析】线段比例尺表示图上距离1cm等于实际距离30km,根据比例尺=图上距离:实际距离,改写成数值比例尺即可。
【解答】解:1cm:30km
=1cm:3000000cm
=1:3000000
答:改成数值比例尺是1:3000000。
故选:C。
【点评】解答此题的关键是掌握比例尺=图上距离:实际距离这个公式。
3.【答案】C
【分析】根据比例尺的意义作答,即比例尺是图上距离与实际距离的比。
【解答】解:6厘米:48千米
=6厘米:4800000厘米
=6:4800000
=1:800000
答:这幅地图的比例尺是1:800000。
故选:C。
【点评】本题主要考查了比例尺的意义,注意图上距离与实际距离的单位要统一。
4.【答案】A
【分析】由线段比例尺可知,图上1厘米表示20千米,根据比例尺=图上距离:实际距离解答即可。
【解答】解:1厘米:20千米
=1厘米:2000000厘米
=1:2000000
答:改写成数值比例尺是1:2000000。
故选:A。
【点评】熟练掌握线段比例尺和数值比例尺的转化是解题的关键。
5.【答案】A
【分析】根据比例尺=图上距离:实际距离,可直接求得这幅图的比例尺。
【解答】解:20km=2000000cm
5:2000000=1:400000
答:图纸的比例尺是1:400000。
故选:A。
【点评】考查了比例尺的意义,表示比例尺的时候,注意统一单位长度。
6.【答案】B
【分析】实际距离和比例尺已知,依据“图上距离=实际距离×比例尺”即可求出试验田的长和宽的图上距离,再与练习本的实际长度比较即可选出合适的答案。
【解答】解:因为180米=18000厘米,60米=6000厘米,
选项A,1800090(厘米),600030(厘米),画在作业纸上,尺寸过大,不符合实际情况,故不合适;
选项B,180009(厘米),60003(厘米),画在作业纸上比较合适;
选项C,180000.9(厘米),60000.3(厘米),画在作业纸上太小,故不合适;
选项D,180000.09(厘米),60000.03(厘米),画在作业纸上太小,故不合适;
故选:B。
【点评】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意结合实际情况。
7.【答案】B
【分析】根据图形放大的意义,把三角形ABC按2:1的比放大,是指把三角形ABC的各边放大到原来的2倍,对应角大小不变,对应线段的比值变,进而推出放大前、后同一个三角形任意两边的比值不变。
【解答】解:如图:
把三角形ABC按2:1的比放大,三角形ABC放大前、后相对应的“三角形的面积”变大了、“∠1的度数”不变、“AB与BC的比值”不变,即三个要素中,不变化的有2个。
故选:B。
【点评】图形放大与缩小后,改变的是大小,形状不变。即放大前、后对应边成比例,对应角大小不变,改变的是面积。
8.【答案】A
【分析】图形放大或缩小后,改变的是大小,形状不变,即原图形长与宽的比和放大或缩小后图形长与宽的比不变。
【解答】解:把一张长方形照片按6:1的比例放大,照片长与宽的比是6:1,即照片长与它的比不变。
故选:A。
【点评】原图形某两条线段的比与放大或缩小后相对应的线段的比不变,改变是大小,即改变的是图形的面积。
二.填空题(共7小题)
9.【答案】20:1,3。
【分析】(1)图上距离和实际距离已知,依据比例尺的意义,即“比例尺=图上距离÷实际距离”即可求出这幅地图的比例尺。
(2)图上距离和比例尺已知,依据“实际距离=图上距离÷比例尺”即可求得这个零件的实际长度。
【解答】解:(1)4cm:2mm
=40mm:2mm
=20:1
答:这幅图的比例尺是20:1。
(2)60.3(厘米)
0.3厘米=3毫米
答:这个零件的实际长度是3毫米.
故答案为:20:1,3。
【点评】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意单位的换算。
10.【答案】1:6000000,3.5。
【分析】由线段比例尺可知,图上1厘米表示实际距离60千米,根据比例尺=图上距离:实际距离可以求出数值比例尺;根据图上距离=实际距离×比例尺求出图上距离。1千米=100000厘米,高级单位转化成低级单位乘进率,低级单位转化成高级单位除以进率。据此解答即可。
【解答】解:60km=6000000cm
则改写成数值比例尺是1:6000000
210km=21000000cm
210000003.5(cm)
答:如果实际距离是210km,那么图上距离是3.5cm。
故答案为:1:6000000,3.5。
【点评】熟练掌握比例尺、图上距离、实际距离的关系是解决此题的关键。
11.【答案】1:50;15:16。
【分析】先统一单位,再根据比例尺=图上距离:实际距离,写出比后再化简即可求得比例尺;再根据比的意义,求出小莉和妈妈实际的身高之比即可。
【解答】解:1.5米=150厘米
3厘米:150厘米=1:50
150厘米:160厘米=15:16
答:这张照片的比例尺是1:50,小莉和妈妈实际的身高之比是15:16。
故答案为:1:50;15:16。
【点评】此题主要考查图上距离、实际距离和比例尺的关系以及比的意义,解答时要注意单位的换算。
12.【答案】见试题解答内容
【分析】这道题是已知图上距离、实际距离,求比例尺,用比例尺=图上距离:实际距离,统一单位代入即可解决问题.
【解答】解:20千米=2000000厘米,
2.5:2000000=1:800000.
答:这幅地图的比例尺是1:800000.
故答案为:1:800000.
【点评】这道题主要考查比例尺的定义:比例尺是图上距离与实际距离的比.
13.【答案】12;20。
【分析】在一定的弹性范围内,橡皮筋相对位置(如点B和点C)的拉长距离成正比例关系。
设点B的位置在x厘米处,根据点B现在的位置:点B原来的位置=点C现在的位置:点C原来的位置,列出比例求出x的值是点B的位置。
设点C的位置在y厘米处,根据点C现在的位置:点C原来的位置=点B现在的位置:点B原来的位置,列出比例求出y的值是点C的位置。
【解答】解:设点B现在的位置在x厘米处。
x:9=16:12
12x=9×16
12x=144
12x÷12=144÷12
x=12
解:设点C现在的位置在y厘米处。
y:12=15:9
9x=12×15
9x=180
9x÷9=180÷9
x=20
如果点A的位置固定不变,将橡皮筋继续拉长,使点C的位置在16厘米处,那么点B的位置在12厘米处;如果使点B的位置在15厘米处,那么点C的位置在20厘米处。
故答案为:12;20。
【点评】解答本题的关键是根据图示确定比例关系,从而列出比例解决问题。
14.【答案】1:5000000,155。
【分析】线段比例尺表示图上1厘米代表实际距离50千米,比例尺=图上距离:实际距离,据此求出数值比例尺;因为图上1厘米代表实际距离50千米,所以宁波到杭州的实际距离是3.1个50千米。
【解答】解:1厘米:50千米
=1厘米:5000000厘米
=1:5000000
50×3.1=155(千米)
答:改成数值比例尺是1:5000000,实际距离是155千米。
故答案为:1:5000000,155。
【点评】明确线段比例尺与数值比例尺的互化的方法是解题的关键。
15.【答案】见试题解答内容
【分析】要求两地的图上距离是多少厘米,根据“实际距离×比例尺=图上距离”,代入数值,计算即可.
【解答】解:500千米=50000000厘米
500000002.5(厘米)
答:甲、乙两地之间的长度是2.5厘米.
故答案为:2.5.
【点评】解答此题应根据图上距离、比例尺和实际距离三者的关系,进行分析解答即可得出结论.
三.判断题(共9小题)
16.【答案】×
【分析】根据比例尺的意义作答,即比例尺是图上距离与实际距离的比.
【解答】解:由线段比例尺可知,图上1厘米表示实际距离240千米,
240千米=24000000厘米,
比例尺是1:24000000.
原题说法错误.
故答案为:×.
【点评】本题主要考查了比例尺的意义,注意图上距离与实际距离的单位要统一.
17.【答案】×
【分析】把长方形按2:1的比例放大,就是把长方形的长和宽都扩大到原来的2倍,根据比的基本性质,长与宽的比是不变的;据此解答即可。
【解答】解:分析可知,把长与宽的比是3:1的长方形按2:1放大后,新长方形的长和宽的比不变,还是3:1。所以原题说法错误。
故答案为:×。
【点评】本题是考查图形的放大与缩小。一个长方形,不论放大或缩小多少倍,长与宽的比不变。
18.【答案】×
【分析】由线段比例尺可知,图上1厘米表示实际距离80千米,据此判断。
【解答】解:在比例中,图上距离1cm表示实际距离80km。
所以原题说法错误。
故答案为:×。
【点评】明确线段比例尺表示的意义是解题的关键。
19.【答案】×
【分析】设原长方形的长为3a,宽为3b,按1:3缩小后长方形的长为a,宽为b。根据长方形的周长计算公式“C=2(a+b)”分别求出原长方形的周长、缩小后长方形的周长,用原长方形的周长除以缩小后长方形的周长;根据长方形的面积计算公式“S=ab”分别求出原长方形的面积,缩小后长方形的面积,用原长方形的面积除以缩小后长方形的面积。然后根据计算结果作出判断。
【解答】解:设原长方形的长为3a,宽为3b,按1:3缩小后长方形的长为a,宽为b。
2(3a+3b)÷2(a+b)
=6(a+b)÷2(a+b)
=3
(3a×3b)÷ab
=9ab÷ab
=9
把一个长方形按边长1:3的比例缩小后,周长会比原来缩小3倍,面积会比原来缩小9倍。
原题说法错误。
故答案为:×。
【点评】本题考查的知识点:图形放大与缩小的意义、长方形周长的计算、长方形面积的计算等。
20.【答案】√
【分析】根据“比例尺=图上距离:实际距离”可知,比例尺1:16000000表示图上1cm相当于16000000cm,然后根据进率:1km=100000cm,换算单位即可。
【解答】解:16000000cm=160km
在比例尺是1:16000000的地图上,图上1cm表示实际的160km。
原题说法正确。
故答案为:√。
【点评】本题考查比例尺的意义以及长度单位的换算。
21.【答案】见试题解答内容
【分析】根据比例尺的意义作答,即比例尺是图上距离与实际距离的比.
【解答】解:6米=600厘米
3:600=1:200
答:这幅图的比例尺是1:200.
故答案为:×.
【点评】本题主要考查了比例尺的意义,注意图上距离与实际距离的单位要统一.
22.【答案】√
【分析】根据比例尺的意义作答,即比例尺是图上距离与实际距离的比。
【解答】解:15千米=1500000厘米
5:1500000=1:300000
答:这幅地图的比例尺是1:300000。
原题说法正确。
故答案为:√。
【点评】本题主要考查了比例尺的意义,注意图上距离与实际距离的单位要统一。
23.【答案】√
【分析】根据图形放大与缩小的意义,图形按比放大(或缩小)时,要使放大(或缩小)前后的图形对应线段的长的比相等,即对称线段成比例。
【解答】解:图形按比放大(或缩小)时,要使放大(或缩小)前后的图形对应线段的长的比相等。
故答案为:√。
【点评】本题考查了图形的放大与缩小,图形放大或缩小后与原图形相似,即对应边成比例(比相等),对应角大小相等。
24.【答案】×
【分析】先统一单位,再根据比例尺=图上距离:实际距离,写出比后再化简即可。
【解答】解:4.5cm:3mm
=45mm:3mm
=45:3
=15:1
答:这幅图的比例尺是15:1
所以原题说法错误。
故答案为:×。
【点评】比例尺=图上距离:实际距离,注意单位要统一。
四.计算题(共2小题)
25.【答案】见试题解答内容
【分析】根据题意可知,缩小后的三角形与原三角形对应边成比例,所以设未知边为x,列比例为:1.6:x=3.2:4.8,利用比例的基本性质解比例即可.
【解答】解:设未知边为x,
1.6:x=3.2:4.8
3.2 x=1.6×4.8
x=2.4
答:未知数为2.4.
【点评】本题主要考查图形的放大与缩小,关键利用放大或缩小后的图形与原图形对应边成比例做题.
26.【答案】见试题解答内容
【分析】根据图上距离:实际距离=比例尺,实际距离=图上距离÷比例尺,图上距离=实际距离×比例尺,据此解答.
【解答】解:
3150000(厘米)
150000厘米=1.5千米
50千米=5000000厘米
2.5:5000000=1:2000000;
180千米=18000000厘米
180000001.5(厘米)
填表如下:
图上距离 实际距离 比例尺
3厘米 1.5千米 1:50000
2.5厘米 50千米 1:2000000
1.5厘米 180千米 1:12000000
故答案为:1.5千米,1:2000000,1.5厘米.
【点评】本题主要考查了比例尺、图上距离与实际距离的关系.
五.操作题(共1小题)
27.【答案】
【分析】直角三角形两直角边即可确定其形状,根据图形放大的意义,把这个三角形的两直角均放大到原来的3倍所得到的图形,就是原图形按3:1放大后的图形。
【解答】解:根据题意画图如下:
【点评】图形放大或缩小后,改变的是大小,形状不变。
六.应用题(共7小题)
28.【答案】2.5小时。
【分析】根据实际距离=图上距离÷比例尺,求出A,B两地的实际距离,再根据相遇时间=总路程÷速度和。
【解答】解:4.812000000(厘米)
12000000厘米=120千米
120÷(12+36)
=120÷48
=2.5(小时)
答:两人2.5小时后相遇。
【点评】此题考查了比例尺、图上距离和实际距离的关系以及时间、速度和路程的关系。
29.【答案】15辆。
【分析】设需要x辆车,因为每辆车坐的人数×车的辆数=总人数(一定),所以每辆车坐的人数与车的辆数成反比例,列式解答即可。
【解答】解:设需要x辆车,
28x=35×12
28x=420
x=15
答:需要15辆车。
【点评】本题主要考查了比例的应用,关键是得出每辆车坐的人数与车的辆数成反比例。
30.【答案】1:5000。
【分析】图上距离和实际距离已知,依据“比例尺=图上距离:实际距离”即可求得这幅图的比例尺。
【解答】解:200米=20000厘米
4厘米:20000厘米=1:5000
答:这幅图的比例尺是1:5000。
【点评】此题主要考查比例尺的计算方法,解答时要注意单位的换算。
31.【答案】见试题解答内容
【分析】图上距离和比例尺已知,依据“实际距离=图上距离÷比例尺”即可求出甲乙两地的实际距离,再据“图上距离=实际距离×比例尺”即可求出在另一幅图上的图上距离.
【解答】解:8.5
=17000000
=3.4(厘米)
答:在另一幅比例尺是1:5000000的地图上,这两地之间的距离是3.4厘米.
【点评】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意单位的换算.
32.【答案】见试题解答内容
【分析】(1)根据实际距离=图上距离÷比例尺,可代入数据分别求出实际的长和宽;
(2)用实际的长乘实际的宽可求出实际的占地面积.据此解答.
【解答】解:(1)0.0550(米)
0.02121(米)
答:泳池实际的长是50米,宽是21米.
(2)50×21=1050(平方米)
答:泳池实际占地面积是1050平方米.
【点评】本题重点考查了学生对实际距离=图上距离÷比例尺和长方形面积公式的掌握.
33.【答案】85千米。
【分析】设原路返回时计划2个小时到达顺平,每小时要行驶x千米,根据“路程=速度×时间”及从顺平到北京,往返的路程相等,即可列比例解答。
【解答】解:每小时要行驶x千米。
2x=68×2.5
2x=170
x=85
答:每小时要行驶85千米。
【点评】列方程解答应用题的关键是设出未知数,再找出含有未知数的等量关系式。
34.【答案】9
【分析】根据速度一定时,路程和时间成正比例,先求出速度,再求出时间即可。
【解答】解:设需要x小时才能到达
540:x=180:3
180x=540×3
x=9
答:需要9小时才能到达。
故答案为:9
【点评】本题是一道比例的应用题,确定速度一定时,路程和时间成正比例是解答此题的关键。
1.比的意义
【知识点归纳】
两个数相除,也叫两个数的比.
2.比例的应用
【知识点归纳】
根据问题中的不变量找出两种相关联的量,并判断这两种相关联的量成什么比例关系,根据正、反比例关系式列出相应的方程并求解.
3.图形的放大与缩小
【知识点归纳】
1.图形的放大和缩小是生活中常见的现象,把一个图形放大或缩小后所得到的图形与元图形相比,形状相同,大小不同.
2.方法:一看、二算、三画.
4.比例尺
【知识点归纳】
1.比例尺:
表示图上距离比实地距离缩小的程度,因此也叫缩尺.图上距离和实际距离的比,叫做这幅图的比例尺.
即:图上距离:实际距离=图上距离÷比例尺
比例尺分类:
比例尺一般分为数值比例尺和线段比例尺:
(1)数值比例尺:例如一幅图的比例尺是1:20000或.为了方便,通常把比例尺写成前项(或后项)是1的比.
(2)线段比例尺是在图上附上一条标有数量的线段,用来表示实际相对应的距离.
2.比例尺表示方法:
用公式表示为:实际距离=图上距离÷比例尺.比例尺通常有三种表示方法.
(1)数字式,用数字的比例式或分数式表示比例尺的大小.例如地图上1厘米代表实地距离500千米,可写成:1:50000000或写成:.
(2)线段式,在地图上画一条线段,并注明地图上1厘米所代表的实际距离.
(3)文字式,在地图上用文字直接写出地图上1厘米代表实地距离多少千米,如:图上1厘米相当于地面距离500千米,或五千万分之一.
3.比例尺公式:
图上距离=实际距离×比例尺
实际距离=图上距离÷比例尺
比例尺=图上距离÷实际距离.
一.选择题(共8小题)
1.阳光小区新建一个长方形健身广场,长100m、宽60m。王叔叔把它画在规格是“30cm×21cm”的图纸上,他应选择哪个比例尺比较合适?( )
A.1:500 B.1:200 C.1000:1 D.1:5000
2.把线段比例尺改成数值比例尺是( )
A.1:30 B.1:90 C.1:3000000 D.1:9000000
3.漳平与华安两地相距48千米,在一幅地图上,量得漳平与华安的图上距离是6厘米,这幅地图的比例尺是( )
A.1:600000 B.1:80000 C.1:800000 D.1:8000000
4.将如图所示的线段比例尺,改写成数值比例尺是( )
A.1:2000000 B.1:4000000 C.1:600000
5.甲、乙两地相距20km,画在设计图纸上的长度是5cm,图纸的比例尺是( )
A.1:400000 B.400000:1 C.1:4 D.4:1
6.一块长方形的试验田,长180米,宽60米,如果把它画成平面示意图,画在一张作业纸上,选用( )比例尺比较合适。
A.1:200 B.1:2000 C.1:20000 D.1:200000
7.如图,把三角形ABC按2:1的比放大,三角形ABC放大前、后相对应的“三角形的面积”、“∠1的度数”、“AB与BC的比值”三个要素中,不变化的有( )个。
A.1 B.2 C.3
8.把一张长方形照片按6:1的比例放大,照片长与宽的比是( )
A.不变 B.变了 C.6;1 D.1:6
二.填空题(共7小题)
9.一个2mm长的精密零件画到图纸上长4cm,那么这幅图的比例尺是( )。如果这幅图纸上有一个零件长6cm,那么这个零件的实际长度是 mm。
10.把如图比例尺改写成数值比例尺是 ;如果实际距离是210km,那么图上距离是 cm。
11.小莉的身高是1.5m,妈妈的身高是160cm,旅游时她和妈妈拍了一张照片,照片上小莉的身高是3cm,这张照片的比例尺是 ,小莉和妈妈实际的身高之比是 。
12.在一幅地图上,用2.5厘米的长度表示实际距离20千米,这幅地图的比例尺是 .
13.如图,欢欢沿着直尺的方向拉橡皮筋。如果点A的位置固定不变,将橡皮筋继续拉长,使点C的位置在16厘米处,那么点B的位置在 厘米处;如果使点B的位置在15厘米处,那么点C的位置在 厘米处。
14.如图是一个线段比例尺,改成数值比例尺是 。测得图上宁波到杭州的
距离是3.1厘米,实际距离是 千米。
15.甲地到乙地的实际距离是500km,在比例尺是1:20000000的地图上,甲、乙两地之间的长度是 厘米.
三.判断题(共9小题)
16.一幅地图的比例尺是,把它改写成数值比例尺是1:2400000. (判断对错)
17.把长与宽的比是3:1的长方形按2:1放大后,新长方形的长和宽的比是6:1。 (判断对错)
18.在比例中,图上距离1cm表示实际距离160km (判断对错)
19.把一个长方形按边长1:3的比例缩小后,周长会比原来缩小3倍,面积会比原来缩小6倍。 (判断对错)
20.在比例尺是1:16000000的地图上,图上1cm表示实际的160km。 (判断对错)
21.在一幅平面图上,图上距离是3厘米,实际距离是6米,这幅图的比例尺是1:2. .(判断对错)
22.一幅地图中某两地的图上距离5cm表示实际距离15km,这幅图的比例尺是1:300000。 (判断对错)
23.图形按比放大时,要使放大前后图形对应线段的比相等。 (判断对错)
24.一个零件长3mm,画在图纸上长4.5cm,这幅图的比例尺是1:15。 (判断对错)
四.计算题(共2小题)
25.将图1的三角形按比例缩小后得到图2的三角形,求未知数x.
26.先计算再填表.
图上距离 实际距离 比例尺
3厘米 1:50000
2.5厘米 50千米
180千米 1:12000000
五.操作题(共1小题)
27.图中每个小方格的面积表示1平方厘米,请将三角形ABC按3:1放大,画在方格纸上。
六.应用题(共7小题)
28.在比例尺1:2500000的的地图上量得A、B两地相距4.8厘米。甲骑自行车以每小时12km的速度从A地骑往B地,同时乙开车以每小时36km的速度从B开往A地。两人几小时后相遇?
29.学校组织同学们参观科技博物馆,如果每辆车坐35人,需要12辆车;如果每辆车坐28人,需要多少辆车?(用比例解)
30.一块长方形菜地,长是200米,量得图纸上长是4厘米,你能求出这幅图的比例尺吗?
31.在一幅比例尺是1:2000000的地图上,量得A、B两地之间的距离是8.5cm,在另一幅比例尺是1:5000000的地图上,这两地之间的距离是多少厘米?
32.游泳比赛的泳池是一个长方形,把泳池的长和宽分别缩小到原来的后图形如下.
(1)泳池实际的长和宽各是多少米?
(2)泳池的实际占地面积是多少平方米?
33.一辆汽车从顺平开往北京,每小时行驶68千米,2.5小时到达,原路返回时计划2个小时到达顺平,每小时要行驶多少千米?(用比例解答)
34.一辆汽车从甲地开往乙地,180千米用了3小时,照这样的速度,乙地到丙地长540千米,需要几小时才能到达?(用比例方法解)
第四单元第11课时比例的应用
参考答案与试题解析
一.选择题(共8小题)
1.【答案】A
【分析】根据图上距离=实际距离×比例尺计算出各选项的图上距离,再结合规格是“30cm×21cm”的图纸解答即可。
【解答】解:100米=10000厘米,60米=6000厘米
A.1000020(厘米)
600012(厘米)
画在规格是“30cm×21cm”的图纸上合适;
B.1000050(厘米)
600030(厘米)
把它画在规格是“30cm×21cm”的图纸上偏大,不合适;
C.1000010000000(厘米)
60006000000(厘米)
把它画在规格是“30cm×21cm”的图纸上太大,不合适;
D.100002(厘米)
60001.2(厘米)
把它画在规格是“30cm×21cm”的图纸上偏小。
故选:A。
【点评】本题考查了实际距离、图上距离、比例尺三者间的关系。
2.【答案】C
【分析】线段比例尺表示图上距离1cm等于实际距离30km,根据比例尺=图上距离:实际距离,改写成数值比例尺即可。
【解答】解:1cm:30km
=1cm:3000000cm
=1:3000000
答:改成数值比例尺是1:3000000。
故选:C。
【点评】解答此题的关键是掌握比例尺=图上距离:实际距离这个公式。
3.【答案】C
【分析】根据比例尺的意义作答,即比例尺是图上距离与实际距离的比。
【解答】解:6厘米:48千米
=6厘米:4800000厘米
=6:4800000
=1:800000
答:这幅地图的比例尺是1:800000。
故选:C。
【点评】本题主要考查了比例尺的意义,注意图上距离与实际距离的单位要统一。
4.【答案】A
【分析】由线段比例尺可知,图上1厘米表示20千米,根据比例尺=图上距离:实际距离解答即可。
【解答】解:1厘米:20千米
=1厘米:2000000厘米
=1:2000000
答:改写成数值比例尺是1:2000000。
故选:A。
【点评】熟练掌握线段比例尺和数值比例尺的转化是解题的关键。
5.【答案】A
【分析】根据比例尺=图上距离:实际距离,可直接求得这幅图的比例尺。
【解答】解:20km=2000000cm
5:2000000=1:400000
答:图纸的比例尺是1:400000。
故选:A。
【点评】考查了比例尺的意义,表示比例尺的时候,注意统一单位长度。
6.【答案】B
【分析】实际距离和比例尺已知,依据“图上距离=实际距离×比例尺”即可求出试验田的长和宽的图上距离,再与练习本的实际长度比较即可选出合适的答案。
【解答】解:因为180米=18000厘米,60米=6000厘米,
选项A,1800090(厘米),600030(厘米),画在作业纸上,尺寸过大,不符合实际情况,故不合适;
选项B,180009(厘米),60003(厘米),画在作业纸上比较合适;
选项C,180000.9(厘米),60000.3(厘米),画在作业纸上太小,故不合适;
选项D,180000.09(厘米),60000.03(厘米),画在作业纸上太小,故不合适;
故选:B。
【点评】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意结合实际情况。
7.【答案】B
【分析】根据图形放大的意义,把三角形ABC按2:1的比放大,是指把三角形ABC的各边放大到原来的2倍,对应角大小不变,对应线段的比值变,进而推出放大前、后同一个三角形任意两边的比值不变。
【解答】解:如图:
把三角形ABC按2:1的比放大,三角形ABC放大前、后相对应的“三角形的面积”变大了、“∠1的度数”不变、“AB与BC的比值”不变,即三个要素中,不变化的有2个。
故选:B。
【点评】图形放大与缩小后,改变的是大小,形状不变。即放大前、后对应边成比例,对应角大小不变,改变的是面积。
8.【答案】A
【分析】图形放大或缩小后,改变的是大小,形状不变,即原图形长与宽的比和放大或缩小后图形长与宽的比不变。
【解答】解:把一张长方形照片按6:1的比例放大,照片长与宽的比是6:1,即照片长与它的比不变。
故选:A。
【点评】原图形某两条线段的比与放大或缩小后相对应的线段的比不变,改变是大小,即改变的是图形的面积。
二.填空题(共7小题)
9.【答案】20:1,3。
【分析】(1)图上距离和实际距离已知,依据比例尺的意义,即“比例尺=图上距离÷实际距离”即可求出这幅地图的比例尺。
(2)图上距离和比例尺已知,依据“实际距离=图上距离÷比例尺”即可求得这个零件的实际长度。
【解答】解:(1)4cm:2mm
=40mm:2mm
=20:1
答:这幅图的比例尺是20:1。
(2)60.3(厘米)
0.3厘米=3毫米
答:这个零件的实际长度是3毫米.
故答案为:20:1,3。
【点评】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意单位的换算。
10.【答案】1:6000000,3.5。
【分析】由线段比例尺可知,图上1厘米表示实际距离60千米,根据比例尺=图上距离:实际距离可以求出数值比例尺;根据图上距离=实际距离×比例尺求出图上距离。1千米=100000厘米,高级单位转化成低级单位乘进率,低级单位转化成高级单位除以进率。据此解答即可。
【解答】解:60km=6000000cm
则改写成数值比例尺是1:6000000
210km=21000000cm
210000003.5(cm)
答:如果实际距离是210km,那么图上距离是3.5cm。
故答案为:1:6000000,3.5。
【点评】熟练掌握比例尺、图上距离、实际距离的关系是解决此题的关键。
11.【答案】1:50;15:16。
【分析】先统一单位,再根据比例尺=图上距离:实际距离,写出比后再化简即可求得比例尺;再根据比的意义,求出小莉和妈妈实际的身高之比即可。
【解答】解:1.5米=150厘米
3厘米:150厘米=1:50
150厘米:160厘米=15:16
答:这张照片的比例尺是1:50,小莉和妈妈实际的身高之比是15:16。
故答案为:1:50;15:16。
【点评】此题主要考查图上距离、实际距离和比例尺的关系以及比的意义,解答时要注意单位的换算。
12.【答案】见试题解答内容
【分析】这道题是已知图上距离、实际距离,求比例尺,用比例尺=图上距离:实际距离,统一单位代入即可解决问题.
【解答】解:20千米=2000000厘米,
2.5:2000000=1:800000.
答:这幅地图的比例尺是1:800000.
故答案为:1:800000.
【点评】这道题主要考查比例尺的定义:比例尺是图上距离与实际距离的比.
13.【答案】12;20。
【分析】在一定的弹性范围内,橡皮筋相对位置(如点B和点C)的拉长距离成正比例关系。
设点B的位置在x厘米处,根据点B现在的位置:点B原来的位置=点C现在的位置:点C原来的位置,列出比例求出x的值是点B的位置。
设点C的位置在y厘米处,根据点C现在的位置:点C原来的位置=点B现在的位置:点B原来的位置,列出比例求出y的值是点C的位置。
【解答】解:设点B现在的位置在x厘米处。
x:9=16:12
12x=9×16
12x=144
12x÷12=144÷12
x=12
解:设点C现在的位置在y厘米处。
y:12=15:9
9x=12×15
9x=180
9x÷9=180÷9
x=20
如果点A的位置固定不变,将橡皮筋继续拉长,使点C的位置在16厘米处,那么点B的位置在12厘米处;如果使点B的位置在15厘米处,那么点C的位置在20厘米处。
故答案为:12;20。
【点评】解答本题的关键是根据图示确定比例关系,从而列出比例解决问题。
14.【答案】1:5000000,155。
【分析】线段比例尺表示图上1厘米代表实际距离50千米,比例尺=图上距离:实际距离,据此求出数值比例尺;因为图上1厘米代表实际距离50千米,所以宁波到杭州的实际距离是3.1个50千米。
【解答】解:1厘米:50千米
=1厘米:5000000厘米
=1:5000000
50×3.1=155(千米)
答:改成数值比例尺是1:5000000,实际距离是155千米。
故答案为:1:5000000,155。
【点评】明确线段比例尺与数值比例尺的互化的方法是解题的关键。
15.【答案】见试题解答内容
【分析】要求两地的图上距离是多少厘米,根据“实际距离×比例尺=图上距离”,代入数值,计算即可.
【解答】解:500千米=50000000厘米
500000002.5(厘米)
答:甲、乙两地之间的长度是2.5厘米.
故答案为:2.5.
【点评】解答此题应根据图上距离、比例尺和实际距离三者的关系,进行分析解答即可得出结论.
三.判断题(共9小题)
16.【答案】×
【分析】根据比例尺的意义作答,即比例尺是图上距离与实际距离的比.
【解答】解:由线段比例尺可知,图上1厘米表示实际距离240千米,
240千米=24000000厘米,
比例尺是1:24000000.
原题说法错误.
故答案为:×.
【点评】本题主要考查了比例尺的意义,注意图上距离与实际距离的单位要统一.
17.【答案】×
【分析】把长方形按2:1的比例放大,就是把长方形的长和宽都扩大到原来的2倍,根据比的基本性质,长与宽的比是不变的;据此解答即可。
【解答】解:分析可知,把长与宽的比是3:1的长方形按2:1放大后,新长方形的长和宽的比不变,还是3:1。所以原题说法错误。
故答案为:×。
【点评】本题是考查图形的放大与缩小。一个长方形,不论放大或缩小多少倍,长与宽的比不变。
18.【答案】×
【分析】由线段比例尺可知,图上1厘米表示实际距离80千米,据此判断。
【解答】解:在比例中,图上距离1cm表示实际距离80km。
所以原题说法错误。
故答案为:×。
【点评】明确线段比例尺表示的意义是解题的关键。
19.【答案】×
【分析】设原长方形的长为3a,宽为3b,按1:3缩小后长方形的长为a,宽为b。根据长方形的周长计算公式“C=2(a+b)”分别求出原长方形的周长、缩小后长方形的周长,用原长方形的周长除以缩小后长方形的周长;根据长方形的面积计算公式“S=ab”分别求出原长方形的面积,缩小后长方形的面积,用原长方形的面积除以缩小后长方形的面积。然后根据计算结果作出判断。
【解答】解:设原长方形的长为3a,宽为3b,按1:3缩小后长方形的长为a,宽为b。
2(3a+3b)÷2(a+b)
=6(a+b)÷2(a+b)
=3
(3a×3b)÷ab
=9ab÷ab
=9
把一个长方形按边长1:3的比例缩小后,周长会比原来缩小3倍,面积会比原来缩小9倍。
原题说法错误。
故答案为:×。
【点评】本题考查的知识点:图形放大与缩小的意义、长方形周长的计算、长方形面积的计算等。
20.【答案】√
【分析】根据“比例尺=图上距离:实际距离”可知,比例尺1:16000000表示图上1cm相当于16000000cm,然后根据进率:1km=100000cm,换算单位即可。
【解答】解:16000000cm=160km
在比例尺是1:16000000的地图上,图上1cm表示实际的160km。
原题说法正确。
故答案为:√。
【点评】本题考查比例尺的意义以及长度单位的换算。
21.【答案】见试题解答内容
【分析】根据比例尺的意义作答,即比例尺是图上距离与实际距离的比.
【解答】解:6米=600厘米
3:600=1:200
答:这幅图的比例尺是1:200.
故答案为:×.
【点评】本题主要考查了比例尺的意义,注意图上距离与实际距离的单位要统一.
22.【答案】√
【分析】根据比例尺的意义作答,即比例尺是图上距离与实际距离的比。
【解答】解:15千米=1500000厘米
5:1500000=1:300000
答:这幅地图的比例尺是1:300000。
原题说法正确。
故答案为:√。
【点评】本题主要考查了比例尺的意义,注意图上距离与实际距离的单位要统一。
23.【答案】√
【分析】根据图形放大与缩小的意义,图形按比放大(或缩小)时,要使放大(或缩小)前后的图形对应线段的长的比相等,即对称线段成比例。
【解答】解:图形按比放大(或缩小)时,要使放大(或缩小)前后的图形对应线段的长的比相等。
故答案为:√。
【点评】本题考查了图形的放大与缩小,图形放大或缩小后与原图形相似,即对应边成比例(比相等),对应角大小相等。
24.【答案】×
【分析】先统一单位,再根据比例尺=图上距离:实际距离,写出比后再化简即可。
【解答】解:4.5cm:3mm
=45mm:3mm
=45:3
=15:1
答:这幅图的比例尺是15:1
所以原题说法错误。
故答案为:×。
【点评】比例尺=图上距离:实际距离,注意单位要统一。
四.计算题(共2小题)
25.【答案】见试题解答内容
【分析】根据题意可知,缩小后的三角形与原三角形对应边成比例,所以设未知边为x,列比例为:1.6:x=3.2:4.8,利用比例的基本性质解比例即可.
【解答】解:设未知边为x,
1.6:x=3.2:4.8
3.2 x=1.6×4.8
x=2.4
答:未知数为2.4.
【点评】本题主要考查图形的放大与缩小,关键利用放大或缩小后的图形与原图形对应边成比例做题.
26.【答案】见试题解答内容
【分析】根据图上距离:实际距离=比例尺,实际距离=图上距离÷比例尺,图上距离=实际距离×比例尺,据此解答.
【解答】解:
3150000(厘米)
150000厘米=1.5千米
50千米=5000000厘米
2.5:5000000=1:2000000;
180千米=18000000厘米
180000001.5(厘米)
填表如下:
图上距离 实际距离 比例尺
3厘米 1.5千米 1:50000
2.5厘米 50千米 1:2000000
1.5厘米 180千米 1:12000000
故答案为:1.5千米,1:2000000,1.5厘米.
【点评】本题主要考查了比例尺、图上距离与实际距离的关系.
五.操作题(共1小题)
27.【答案】
【分析】直角三角形两直角边即可确定其形状,根据图形放大的意义,把这个三角形的两直角均放大到原来的3倍所得到的图形,就是原图形按3:1放大后的图形。
【解答】解:根据题意画图如下:
【点评】图形放大或缩小后,改变的是大小,形状不变。
六.应用题(共7小题)
28.【答案】2.5小时。
【分析】根据实际距离=图上距离÷比例尺,求出A,B两地的实际距离,再根据相遇时间=总路程÷速度和。
【解答】解:4.812000000(厘米)
12000000厘米=120千米
120÷(12+36)
=120÷48
=2.5(小时)
答:两人2.5小时后相遇。
【点评】此题考查了比例尺、图上距离和实际距离的关系以及时间、速度和路程的关系。
29.【答案】15辆。
【分析】设需要x辆车,因为每辆车坐的人数×车的辆数=总人数(一定),所以每辆车坐的人数与车的辆数成反比例,列式解答即可。
【解答】解:设需要x辆车,
28x=35×12
28x=420
x=15
答:需要15辆车。
【点评】本题主要考查了比例的应用,关键是得出每辆车坐的人数与车的辆数成反比例。
30.【答案】1:5000。
【分析】图上距离和实际距离已知,依据“比例尺=图上距离:实际距离”即可求得这幅图的比例尺。
【解答】解:200米=20000厘米
4厘米:20000厘米=1:5000
答:这幅图的比例尺是1:5000。
【点评】此题主要考查比例尺的计算方法,解答时要注意单位的换算。
31.【答案】见试题解答内容
【分析】图上距离和比例尺已知,依据“实际距离=图上距离÷比例尺”即可求出甲乙两地的实际距离,再据“图上距离=实际距离×比例尺”即可求出在另一幅图上的图上距离.
【解答】解:8.5
=17000000
=3.4(厘米)
答:在另一幅比例尺是1:5000000的地图上,这两地之间的距离是3.4厘米.
【点评】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意单位的换算.
32.【答案】见试题解答内容
【分析】(1)根据实际距离=图上距离÷比例尺,可代入数据分别求出实际的长和宽;
(2)用实际的长乘实际的宽可求出实际的占地面积.据此解答.
【解答】解:(1)0.0550(米)
0.02121(米)
答:泳池实际的长是50米,宽是21米.
(2)50×21=1050(平方米)
答:泳池实际占地面积是1050平方米.
【点评】本题重点考查了学生对实际距离=图上距离÷比例尺和长方形面积公式的掌握.
33.【答案】85千米。
【分析】设原路返回时计划2个小时到达顺平,每小时要行驶x千米,根据“路程=速度×时间”及从顺平到北京,往返的路程相等,即可列比例解答。
【解答】解:每小时要行驶x千米。
2x=68×2.5
2x=170
x=85
答:每小时要行驶85千米。
【点评】列方程解答应用题的关键是设出未知数,再找出含有未知数的等量关系式。
34.【答案】9
【分析】根据速度一定时,路程和时间成正比例,先求出速度,再求出时间即可。
【解答】解:设需要x小时才能到达
540:x=180:3
180x=540×3
x=9
答:需要9小时才能到达。
故答案为:9
【点评】本题是一道比例的应用题,确定速度一定时,路程和时间成正比例是解答此题的关键。
