沪教版(五四)九年级数学下册第27章检测题(附答案)
文档属性
| 名称 | 沪教版(五四)九年级数学下册第27章检测题(附答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 199.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-29 10:59:34 | ||
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
沪教版(五四)九年级数学下册第27章检测题(附答案)
姓名:__________ 班级:__________考号:__________
一、单选题(共12题;共24分)
1.垂径定理及推论中的四条性质:①经过圆心;②垂直于弦;③平分弦;④平分弦所对的弧.由上述四条性质组成的命题中,其中是假命题的是( )
A. ①② ③④ B. ①③ ②④ C. ①④ ②③ D. ②③ ①④
2.设P为⊙O外一点,若点P到⊙O的最短距离为3,最长距离为7,则⊙O的半径为( )
A. 3 B. 2 C. 4或10 D. 2或5
3.已知两圆相外切,连心线长度是10厘米,其中一圆的半径为6厘米,则另一圆的半径是 ( )
A. 16厘米 B. 10厘米 C. 6厘米 D. 4厘米
4.已知⊙O的半径是10cm, 是120°,那么弦AB的弦心距是( )
A. 5cm B. C. D.
5.如图,在8×4的方格(每个方格的边长为1个单位长)中,⊙A的半径为1,⊙B的半径为2,将⊙A由图示位置向右平移1个单位长后,⊙A与静止的⊙B的位置关系是( )
A. 内含 B. 内切 C. 相交 D. 外切
6.下列条件中,能确定圆的是( )
A. 以点O为圆心 B. 以2cm长为半径 C. 以点O为圆心,以5cm长为半径 D. 经过已知点A
7.两圆的半径为5cm和3cm,若圆心距为7cm,则两圆的位置关系是( )
A. 外离 B. 外切 C. 相交 D. 内切
8.如图,从一块直径为 的圆形铁皮上剪出一个圆心角为90°的扇形.则此扇形的面积为( )
A. B. C. D.
9.下列说法中正确的是( )
①圆心角是顶点在圆心的角;②两个圆心角相等,它们所对的弦相等;③两条弦相等,圆心到这两弦的距离相等;④在等圆中,圆心角不变,所对的弦也不变.
A. ①③ B. ②④ C. ①④ D. ②③
10.已知两圆半径分别为4和7,圆心距为3,那么这两个圆的位置关系是( )
A. 内含 B. 内切 C. 相交 D. 外切
11.如图,⊙O1、⊙O2内切于点A,其半径分别是6和3,将⊙O2沿直线O1O2平移至两圆外切时,则点O2移动的长度是( )
A. 3 B. 6 C. 12 D. 6或12
12.如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0)直线y=kx-3k+4与 交于B、C两点,则弦BC的长的最小值为( )
A. 22 B. 24 C. D.
二、填空题(共8题;共18分)
13.若扇形的圆心角为60°,弧长为2π,则扇形的半径为________.
14.已知扇形的弧长为π,半径为1,则该扇形的面积为________
15.阅读下面材料:
在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
尺规作图:过圆外一点作图的切线。
已知:P为圆O外一点。
求作:经过点P的圆O的切线。
小敏的作法如下:
①连接OP,作线段OP的垂直平分线MN交OP于点C;
②以点C为圆心,CO的长为半径作圆交圆O于A、B两点;
③作直线PA、PB,所以直线PA、PB就是所求作的切线。
老师认为小敏的作法正确.
请回答:连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是________;由此可证明直线PA,PB都是⊙O的切线,其依据是________
16.如图是一个古代车轮的碎片,小明为求其外圆半径,连结外圆上的两点A、B,并使AB与车轮内圆相切于点D,做CD⊥AB交外圆于点C.测得CD=10cm,AB=60cm,则这个车轮的外圆半径为________cm.
17.若一个扇形的圆心角为60°,面积为6π,则这个扇形的半径为________.
18.若A(1,2),B(3,﹣3),C(x,y)三点可以确定一个圆,则x、y需要满足的条件是________.
19.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:
①∠BOC=90 +∠A; ②以E为圆心、BE为半径的圆与以F为圆心、CF为半径的圆外切;③设OD=m,AE+AF=n,则S△AEF=mn; ④EF是△ABC的中位线.其中正确的结论是________.
20.在Rt△ABC中,斜边AB=4,∠B=60°,将△ABC绕点B旋转60°,顶点C运动的路线长是 ________(结果保留π).
三、解答题(共4题;共28分)
21.已知如图所示,A,B,C是⊙O上三点,∠AOB=120°,C是的中点,试判断四边形OACB形状,并说明理由.
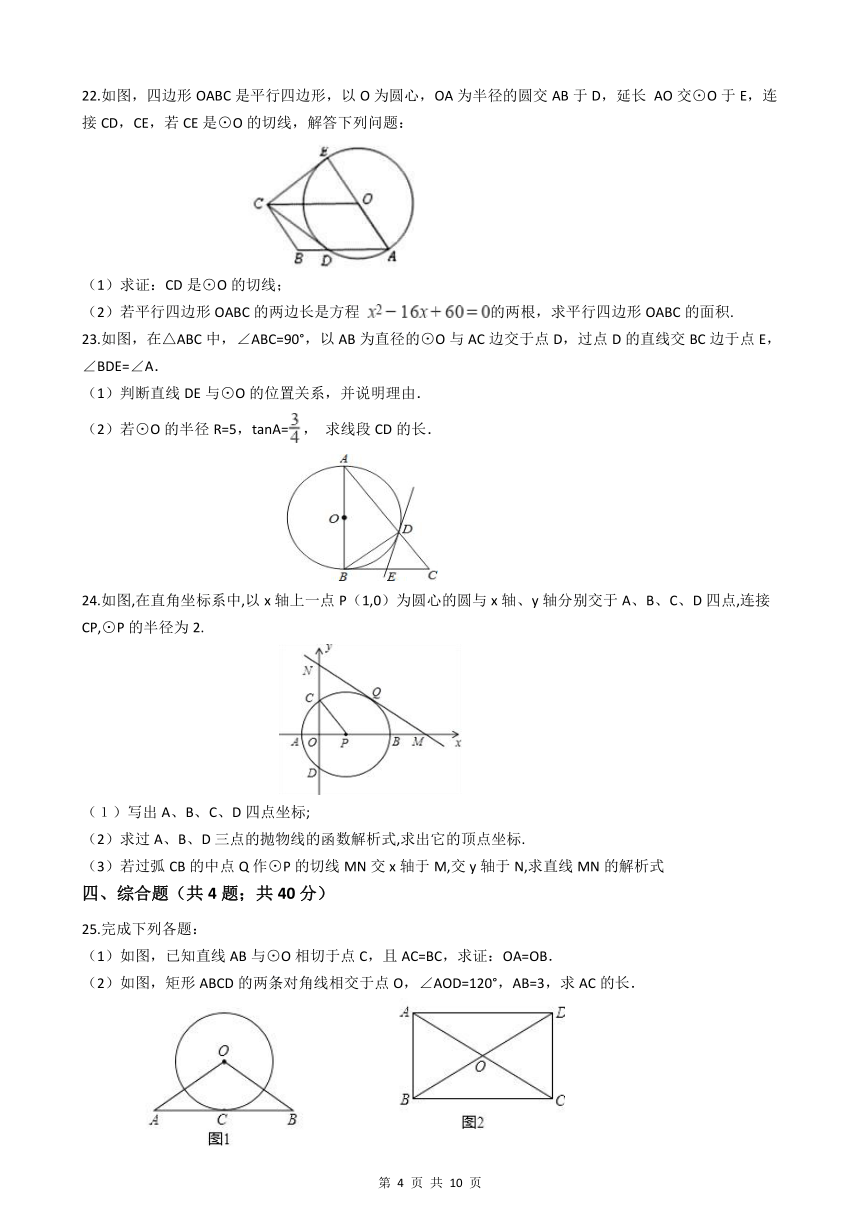
22.如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长 AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若平行四边形OABC的两边长是方程 的两根,求平行四边形OABC的面积.
23.如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D的直线交BC边于点E,∠BDE=∠A.
(1)判断直线DE与⊙O的位置关系,并说明理由.
(2)若⊙O的半径R=5,tanA=, 求线段CD的长.
24.如图,在直角坐标系中,以x轴上一点P(1,0)为圆心的圆与x轴、y轴分别交于A、B、C、D四点,连接CP,⊙P的半径为2.
(1)写出A、B、C、D四点坐标;
(2)求过A、B、D三点的抛物线的函数解析式,求出它的顶点坐标.
(3)若过弧CB的中点Q作⊙P的切线MN交x轴于M,交y轴于N,求直线MN的解析式
四、综合题(共4题;共40分)
25.完成下列各题:
(1)如图,已知直线AB与⊙O相切于点C,且AC=BC,求证:OA=OB.
(2)如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AB=3,求AC的长.
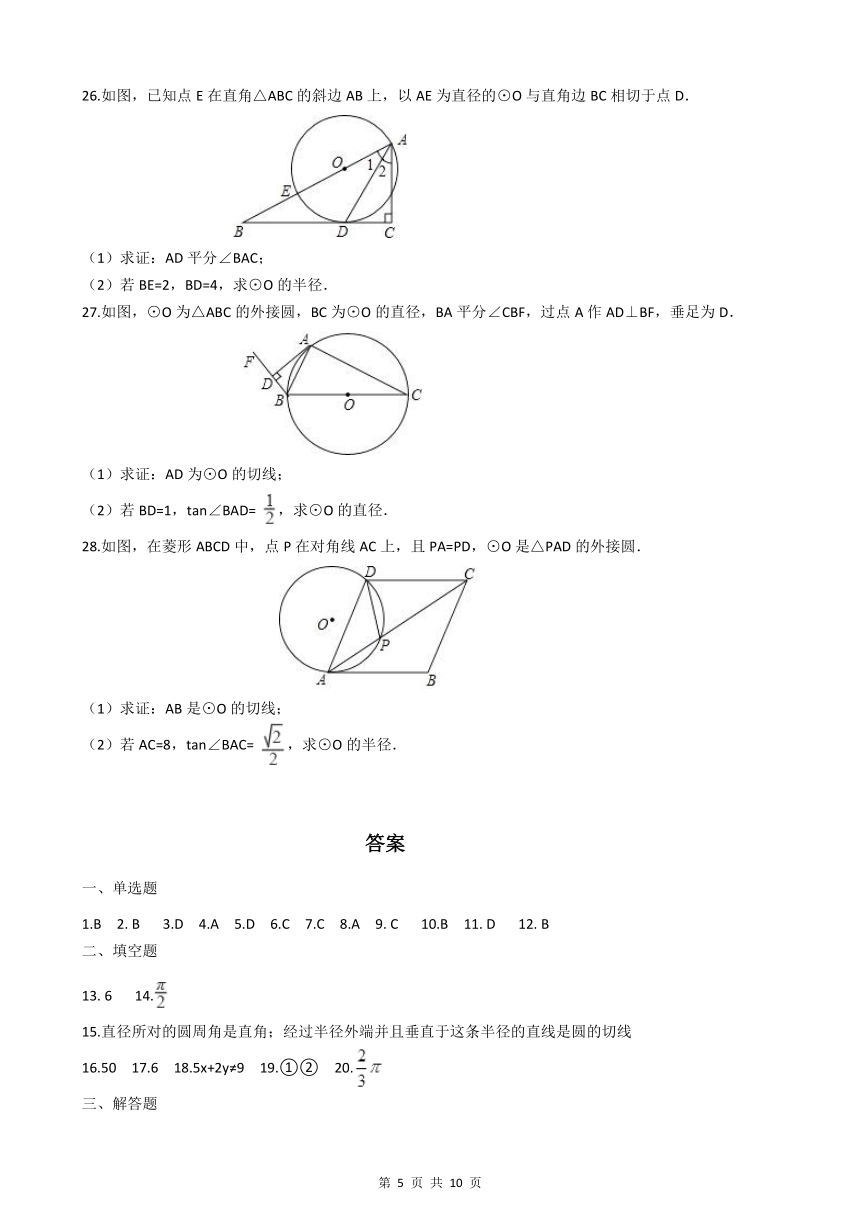
26.如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D.
(1)求证:AD平分∠BAC;
(2)若BE=2,BD=4,求⊙O的半径.
27.如图,⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBF,过点A作AD⊥BF,垂足为D.
(1)求证:AD为⊙O的切线;
(2)若BD=1,tan∠BAD= ,求⊙O的直径.
28.如图,在菱形ABCD中,点P在对角线AC上,且PA=PD,⊙O是△PAD的外接圆.
(1)求证:AB是⊙O的切线;
(2)若AC=8,tan∠BAC= ,求⊙O的半径.
答案
一、单选题
1.B 2. B 3.D 4.A 5.D 6.C 7.C 8.A 9. C 10.B 11. D 12. B
二、填空题
13. 6 14.
15.直径所对的圆周角是直角;经过半径外端并且垂直于这条半径的直线是圆的切线
16.50 17.6 18.5x+2y≠9 19.①② 20.
三、解答题
21.解:AOBC是菱形.
证明:连OC,如图:
∵C是的中点
∴∠AOC=∠BOC=×120°=60°
∵CO=BO(⊙O的半径),
∴△OBC是等边三角形
∴OB=BC
同理△OCA是等边三角形
∴OA=AC
又∵OA=OB
∴OA=AC=BC=BO
∴AOBC是菱形.
22.(1)解:连OD,∵CE是⊙O的切线, ∠OEC=90O , ∵OD=OA,∴∠ODA=∠OAD,又∵OC//AD
∴∠OAD =∠EOC,∠DOC=∠ODA,
∴∠EOC=∠DOC,
又∵OD=OE,OC=OC,
∴△ODC≌△OEC(SAS)
∴∠ODC=∠OEC=90°,
∴CD是⊙O的切线
(2)解: , ,
即OC=10,OA=6.
在Rt△ODC,CD=8
∵△ODC≌△OEC,CE=CD=8
∴平行四边形OABC的面积S=OA×CE=6×8=48
23.解:(1)直线DE与⊙O相切.
理由如下:连接OD.
∵OA=OD
∴∠ODA=∠A
又∵∠BDE=∠A
∴∠ODA=∠BDE
∵AB是⊙O直径
∴∠ADB=90°
即∠ODA+∠ODB=90°
∴∠BDE+∠ODB=90°
∴∠ODE=90°
∴OD⊥DE
∴DE与⊙O相切;
(2)∵R=5,
∴AB=10,
在Rt△ABC中
∵tanA==
∴BC=AB tanA=10×=,
∴AC===,
∵∠BDC=∠ABC=90°,∠BCD=∠ACB
∴△BCD∽△ACB
∴
∴CD===.
24.解:(1)∵P(1,0),⊙P的半径是2,
∴OA=2-1=1,OB=2+1=3,
在Rt△COP中,PC=2,OP=1,由勾股定理得:OC=,
由垂径定理得:OD=OC=,
∴A(-1,0),B(3,0),C(0,),D(0,);
(2)设函数解析式为y=ax2+bx+c
∵A(-1,0),B(3,0),D(0,)
∴
解得:,
所以函数解析式为:y=x2-x-,
y=x2-x-=(x-1)2-,它的顶点坐标为:(1,);
(3)连接PQ,
在Rt△COP中sin∠CPO=,
∴∠CPO=60°,
∵Q为弧BC的中点,
∴∠CPQ=∠BPQ=(180°-60°)=60°,
∵MN切⊙P于Q,
∴∠PQM=90°,
∴∠QMP=30°,
∵PQ=2,
∴PM=2PQ=4,
在Rt△MON中,MN=2ON,
∵MN2=ON2+OM2,
∴(2ON)2=ON2+(1+4)2,
∴ON=,
∴M(5,0),N(0,),
设直线MN的解析式是y=kx+b,
代入得:,
解得:k=,b=,
∴直线MN的解析式是y=x+.
四、综合题
25.(1)证明:连接OC, ∵直线AB与⊙O相切于点C,
∴OC⊥AB,
又∵AC=BC,
∴OC垂直平分AB,
∴OA=OB
(2)证明:∵四边形ABCD是矩形, ∴AC=BD,OA=OC= AC,BO=DO= BD,∠BAD=90°,
∴OA=OB,
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴∠ABO=60°,∠ADB=30°,
∴AC=BD=2AB=6cm
26.(1)证明:连接OD,
∵BC是⊙O的切线,
∴OD⊥BC,
又∵AC⊥BC,
∴OD∥AC,
∴∠2=∠3;
∵OA=OD,
∴∠1=∠3,
∴∠1=∠2,
∴AD平分∠BAC
(2)解:∵BC与圆相切于点D. ∴BD2=BE BA,
∵BE=2,BD=4,
∴BA=8,
∴AE=AB﹣BE=6,
∴⊙O的半径为3
27.(1)证明:连接OA,
∵BC为⊙O的直径,BA平分∠CBF,AD⊥BF,
∴∠ADB=∠BAC=90°,∠DBA=∠CBA;
∵∠OAC=∠OCA,
∴∠DAO=∠DAB+∠BAO=∠BAO+∠OAC=90°,
∴DA为⊙O的切线
(2)解:∵BD=1,tan∠BAD= ,
∴AD=2,
∴AB= = ,
∴cos∠DBA= ;
∵∠DBA=∠CBA,
∴BC= = =5.
∴⊙O的直径为5.
28.(1)解:连结OP、OA,OP交AD于E,如图, ∵PA=PD,
∴弧AP=弧DP,
∴OP⊥AD,AE=DE,
∴∠1+∠OPA=90°,
∵OP=OA,
∴∠OAP=∠OPA,
∴∠1+∠OAP=90°,
∵四边形ABCD为菱形,
∴∠1=∠2,
∴∠2+∠OAP=90°,
∴OA⊥AB,
∴直线AB与⊙O相切;
(2)解:连结BD,交AC于点F,如图, ∵四边形ABCD为菱形,
∴DB与AC互相垂直平分,
∵AC=8,tan∠BAC= ,
∴AF=4,tan∠DAC= = ,
∴DF=2 ,
∴AD= =2 ,
∴AE= ,
在Rt△PAE中,tan∠1= = ,
∴PE= ,
设⊙O的半径为R,则OE=R﹣ ,OA=R,
在Rt△OAE中,∵OA2=OE2+AE2 ,
∴R2=(R﹣ )2+( )2 ,
∴R= ,
即⊙O的半径为 .
(
第
- 1 -
页 共
13
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
沪教版(五四)九年级数学下册第27章检测题(附答案)
姓名:__________ 班级:__________考号:__________
一、单选题(共12题;共24分)
1.垂径定理及推论中的四条性质:①经过圆心;②垂直于弦;③平分弦;④平分弦所对的弧.由上述四条性质组成的命题中,其中是假命题的是( )
A. ①② ③④ B. ①③ ②④ C. ①④ ②③ D. ②③ ①④
2.设P为⊙O外一点,若点P到⊙O的最短距离为3,最长距离为7,则⊙O的半径为( )
A. 3 B. 2 C. 4或10 D. 2或5
3.已知两圆相外切,连心线长度是10厘米,其中一圆的半径为6厘米,则另一圆的半径是 ( )
A. 16厘米 B. 10厘米 C. 6厘米 D. 4厘米
4.已知⊙O的半径是10cm, 是120°,那么弦AB的弦心距是( )
A. 5cm B. C. D.
5.如图,在8×4的方格(每个方格的边长为1个单位长)中,⊙A的半径为1,⊙B的半径为2,将⊙A由图示位置向右平移1个单位长后,⊙A与静止的⊙B的位置关系是( )
A. 内含 B. 内切 C. 相交 D. 外切
6.下列条件中,能确定圆的是( )
A. 以点O为圆心 B. 以2cm长为半径 C. 以点O为圆心,以5cm长为半径 D. 经过已知点A
7.两圆的半径为5cm和3cm,若圆心距为7cm,则两圆的位置关系是( )
A. 外离 B. 外切 C. 相交 D. 内切
8.如图,从一块直径为 的圆形铁皮上剪出一个圆心角为90°的扇形.则此扇形的面积为( )
A. B. C. D.
9.下列说法中正确的是( )
①圆心角是顶点在圆心的角;②两个圆心角相等,它们所对的弦相等;③两条弦相等,圆心到这两弦的距离相等;④在等圆中,圆心角不变,所对的弦也不变.
A. ①③ B. ②④ C. ①④ D. ②③
10.已知两圆半径分别为4和7,圆心距为3,那么这两个圆的位置关系是( )
A. 内含 B. 内切 C. 相交 D. 外切
11.如图,⊙O1、⊙O2内切于点A,其半径分别是6和3,将⊙O2沿直线O1O2平移至两圆外切时,则点O2移动的长度是( )
A. 3 B. 6 C. 12 D. 6或12
12.如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0)直线y=kx-3k+4与 交于B、C两点,则弦BC的长的最小值为( )
A. 22 B. 24 C. D.
二、填空题(共8题;共18分)
13.若扇形的圆心角为60°,弧长为2π,则扇形的半径为________.
14.已知扇形的弧长为π,半径为1,则该扇形的面积为________
15.阅读下面材料:
在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
尺规作图:过圆外一点作图的切线。
已知:P为圆O外一点。
求作:经过点P的圆O的切线。
小敏的作法如下:
①连接OP,作线段OP的垂直平分线MN交OP于点C;
②以点C为圆心,CO的长为半径作圆交圆O于A、B两点;
③作直线PA、PB,所以直线PA、PB就是所求作的切线。
老师认为小敏的作法正确.
请回答:连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是________;由此可证明直线PA,PB都是⊙O的切线,其依据是________
16.如图是一个古代车轮的碎片,小明为求其外圆半径,连结外圆上的两点A、B,并使AB与车轮内圆相切于点D,做CD⊥AB交外圆于点C.测得CD=10cm,AB=60cm,则这个车轮的外圆半径为________cm.
17.若一个扇形的圆心角为60°,面积为6π,则这个扇形的半径为________.
18.若A(1,2),B(3,﹣3),C(x,y)三点可以确定一个圆,则x、y需要满足的条件是________.
19.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:
①∠BOC=90 +∠A; ②以E为圆心、BE为半径的圆与以F为圆心、CF为半径的圆外切;③设OD=m,AE+AF=n,则S△AEF=mn; ④EF是△ABC的中位线.其中正确的结论是________.
20.在Rt△ABC中,斜边AB=4,∠B=60°,将△ABC绕点B旋转60°,顶点C运动的路线长是 ________(结果保留π).
三、解答题(共4题;共28分)
21.已知如图所示,A,B,C是⊙O上三点,∠AOB=120°,C是的中点,试判断四边形OACB形状,并说明理由.
22.如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长 AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若平行四边形OABC的两边长是方程 的两根,求平行四边形OABC的面积.
23.如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D的直线交BC边于点E,∠BDE=∠A.
(1)判断直线DE与⊙O的位置关系,并说明理由.
(2)若⊙O的半径R=5,tanA=, 求线段CD的长.
24.如图,在直角坐标系中,以x轴上一点P(1,0)为圆心的圆与x轴、y轴分别交于A、B、C、D四点,连接CP,⊙P的半径为2.
(1)写出A、B、C、D四点坐标;
(2)求过A、B、D三点的抛物线的函数解析式,求出它的顶点坐标.
(3)若过弧CB的中点Q作⊙P的切线MN交x轴于M,交y轴于N,求直线MN的解析式
四、综合题(共4题;共40分)
25.完成下列各题:
(1)如图,已知直线AB与⊙O相切于点C,且AC=BC,求证:OA=OB.
(2)如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AB=3,求AC的长.
26.如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D.
(1)求证:AD平分∠BAC;
(2)若BE=2,BD=4,求⊙O的半径.
27.如图,⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBF,过点A作AD⊥BF,垂足为D.
(1)求证:AD为⊙O的切线;
(2)若BD=1,tan∠BAD= ,求⊙O的直径.
28.如图,在菱形ABCD中,点P在对角线AC上,且PA=PD,⊙O是△PAD的外接圆.
(1)求证:AB是⊙O的切线;
(2)若AC=8,tan∠BAC= ,求⊙O的半径.
答案
一、单选题
1.B 2. B 3.D 4.A 5.D 6.C 7.C 8.A 9. C 10.B 11. D 12. B
二、填空题
13. 6 14.
15.直径所对的圆周角是直角;经过半径外端并且垂直于这条半径的直线是圆的切线
16.50 17.6 18.5x+2y≠9 19.①② 20.
三、解答题
21.解:AOBC是菱形.
证明:连OC,如图:
∵C是的中点
∴∠AOC=∠BOC=×120°=60°
∵CO=BO(⊙O的半径),
∴△OBC是等边三角形
∴OB=BC
同理△OCA是等边三角形
∴OA=AC
又∵OA=OB
∴OA=AC=BC=BO
∴AOBC是菱形.
22.(1)解:连OD,∵CE是⊙O的切线, ∠OEC=90O , ∵OD=OA,∴∠ODA=∠OAD,又∵OC//AD
∴∠OAD =∠EOC,∠DOC=∠ODA,
∴∠EOC=∠DOC,
又∵OD=OE,OC=OC,
∴△ODC≌△OEC(SAS)
∴∠ODC=∠OEC=90°,
∴CD是⊙O的切线
(2)解: , ,
即OC=10,OA=6.
在Rt△ODC,CD=8
∵△ODC≌△OEC,CE=CD=8
∴平行四边形OABC的面积S=OA×CE=6×8=48
23.解:(1)直线DE与⊙O相切.
理由如下:连接OD.
∵OA=OD
∴∠ODA=∠A
又∵∠BDE=∠A
∴∠ODA=∠BDE
∵AB是⊙O直径
∴∠ADB=90°
即∠ODA+∠ODB=90°
∴∠BDE+∠ODB=90°
∴∠ODE=90°
∴OD⊥DE
∴DE与⊙O相切;
(2)∵R=5,
∴AB=10,
在Rt△ABC中
∵tanA==
∴BC=AB tanA=10×=,
∴AC===,
∵∠BDC=∠ABC=90°,∠BCD=∠ACB
∴△BCD∽△ACB
∴
∴CD===.
24.解:(1)∵P(1,0),⊙P的半径是2,
∴OA=2-1=1,OB=2+1=3,
在Rt△COP中,PC=2,OP=1,由勾股定理得:OC=,
由垂径定理得:OD=OC=,
∴A(-1,0),B(3,0),C(0,),D(0,);
(2)设函数解析式为y=ax2+bx+c
∵A(-1,0),B(3,0),D(0,)
∴
解得:,
所以函数解析式为:y=x2-x-,
y=x2-x-=(x-1)2-,它的顶点坐标为:(1,);
(3)连接PQ,
在Rt△COP中sin∠CPO=,
∴∠CPO=60°,
∵Q为弧BC的中点,
∴∠CPQ=∠BPQ=(180°-60°)=60°,
∵MN切⊙P于Q,
∴∠PQM=90°,
∴∠QMP=30°,
∵PQ=2,
∴PM=2PQ=4,
在Rt△MON中,MN=2ON,
∵MN2=ON2+OM2,
∴(2ON)2=ON2+(1+4)2,
∴ON=,
∴M(5,0),N(0,),
设直线MN的解析式是y=kx+b,
代入得:,
解得:k=,b=,
∴直线MN的解析式是y=x+.
四、综合题
25.(1)证明:连接OC, ∵直线AB与⊙O相切于点C,
∴OC⊥AB,
又∵AC=BC,
∴OC垂直平分AB,
∴OA=OB
(2)证明:∵四边形ABCD是矩形, ∴AC=BD,OA=OC= AC,BO=DO= BD,∠BAD=90°,
∴OA=OB,
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴∠ABO=60°,∠ADB=30°,
∴AC=BD=2AB=6cm
26.(1)证明:连接OD,
∵BC是⊙O的切线,
∴OD⊥BC,
又∵AC⊥BC,
∴OD∥AC,
∴∠2=∠3;
∵OA=OD,
∴∠1=∠3,
∴∠1=∠2,
∴AD平分∠BAC
(2)解:∵BC与圆相切于点D. ∴BD2=BE BA,
∵BE=2,BD=4,
∴BA=8,
∴AE=AB﹣BE=6,
∴⊙O的半径为3
27.(1)证明:连接OA,
∵BC为⊙O的直径,BA平分∠CBF,AD⊥BF,
∴∠ADB=∠BAC=90°,∠DBA=∠CBA;
∵∠OAC=∠OCA,
∴∠DAO=∠DAB+∠BAO=∠BAO+∠OAC=90°,
∴DA为⊙O的切线
(2)解:∵BD=1,tan∠BAD= ,
∴AD=2,
∴AB= = ,
∴cos∠DBA= ;
∵∠DBA=∠CBA,
∴BC= = =5.
∴⊙O的直径为5.
28.(1)解:连结OP、OA,OP交AD于E,如图, ∵PA=PD,
∴弧AP=弧DP,
∴OP⊥AD,AE=DE,
∴∠1+∠OPA=90°,
∵OP=OA,
∴∠OAP=∠OPA,
∴∠1+∠OAP=90°,
∵四边形ABCD为菱形,
∴∠1=∠2,
∴∠2+∠OAP=90°,
∴OA⊥AB,
∴直线AB与⊙O相切;
(2)解:连结BD,交AC于点F,如图, ∵四边形ABCD为菱形,
∴DB与AC互相垂直平分,
∵AC=8,tan∠BAC= ,
∴AF=4,tan∠DAC= = ,
∴DF=2 ,
∴AD= =2 ,
∴AE= ,
在Rt△PAE中,tan∠1= = ,
∴PE= ,
设⊙O的半径为R,则OE=R﹣ ,OA=R,
在Rt△OAE中,∵OA2=OE2+AE2 ,
∴R2=(R﹣ )2+( )2 ,
∴R= ,
即⊙O的半径为 .
(
第
- 1 -
页 共
13
页
)
