第五章 基本平面图形 4 角的比较(含答案)
文档属性
| 名称 | 第五章 基本平面图形 4 角的比较(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-27 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第五章 基本平面图形
4 角的比较
1.若∠1=75°24',∠2=75.3°,∠3=75.12°, 则 ( )
A.∠1=∠2 B.∠2=∠3 C.∠1=∠3 D.以上都不对
2. 如图, ∠AOB = ∠COD, 则∠AOC 与∠DOB 的大小关系是 ( )
A.∠AOC>∠DOB B.∠AOC<∠DOB
C.∠AOC=∠DOB D.∠AOC与∠DOB无法比较大小
3.只利用一副(两块)三角尺不能直接拼出的角度是 ( )
A.75° B.105° C.150° D.165°
4.如图,OC 为∠AOB 内的一条射线,下列条件中不能确定OC平分∠AOB 的是( )
A.∠AOC=∠BOC B.∠AOC+∠COB=∠AOB C.∠AOB=2∠BOC
第4 题图 第5 题图
5.在学习角的过程中,小丽将一副三角板的直角顶点重合放置于A 处,然后将两块三角板在同一平面内绕着点 A 自由转动,她发现在转动的过程中∠CAD和∠BAE的和始终保持不变.则下列结论正确的是 ( )
6.如图,直线 AB,CD 相交于点O, OF 平分 若 则的度数为 ( )
第 6 题图 第 7题图
7.如图,点O为直线 AB 上一点,∠COD=90°,OE平分∠AOC,OG平分∠BOC,OF平分∠BOD,下列结论:①∠EOG=90°②∠DOE+∠BOF=180°③∠AOC-∠BOD= 90° ④∠DOG= 其中正确的有 ( )
A.①②③ B. ①②④ C.①③④ D.①②③④
8.如图, OC 平分 下列四个等式中正确的是 ( )
① ②∠DOC=2∠BOC ③ ④∠COD=3∠COB
A.①② B. ②③ C.③④ D.①④
9.如图,点O在直线 AB 上,OM 平分∠AOC,ON 平分∠BOC, 如果∠COM=2∠CON,则∠CON的度数为__________.
第9题图 第 10题图
10.如图,∠AOB=120°,∠BOC=30°,OD 是∠AOC的平分线,则∠BOD=__________.
11.已知一副三角板如图摆放,两个直角有公共的顶点,∠α=47°42',则∠β=___________(用度,分表示).
第 11题图 第 12题图
12.如图,OM 是∠AOB 的平分线,射线OC 在∠BOM 内部,ON 是∠BOC的平分线,已知 ∠AOC=80°,那么∠MON的大小等于__________°.
13.已知∠AOB=50°,由定点O引一条射线,使得∠BOC=30°,OM,ON 分别是∠AOB 和 ∠BOC 的平分线,则∠MON=__________°.
14.将三角板COD的直角顶点O 放置在直线AB 上(如图),若∠AOC=64°,射线 OE 平分 ∠BOC,则∠DOE的大小为___________.
15.如图,将两块直角三角板的直角顶点 C 叠放在一起.
(1)比较大小:∠ACE ______∠BCD;(填“>”“=”或“<”)
(2)若∠DCE=40°,求∠ACB的度数;
(3)猜想∠ACB 与∠DCE的数量关系,并说明理由.
16.已知点O是直线 AB 上的 一 点,∠COD 是 直角, OE 平分∠BOC.
(1) 如图 1,若∠AOC=30°,求∠COE,∠DOB的度数;
(2)将图 1 中的∠COD绕顶点O 顺时针旋转至图2 的位置,探究∠AOC 与∠DOE的度数之间的数量关系,并说明理由.
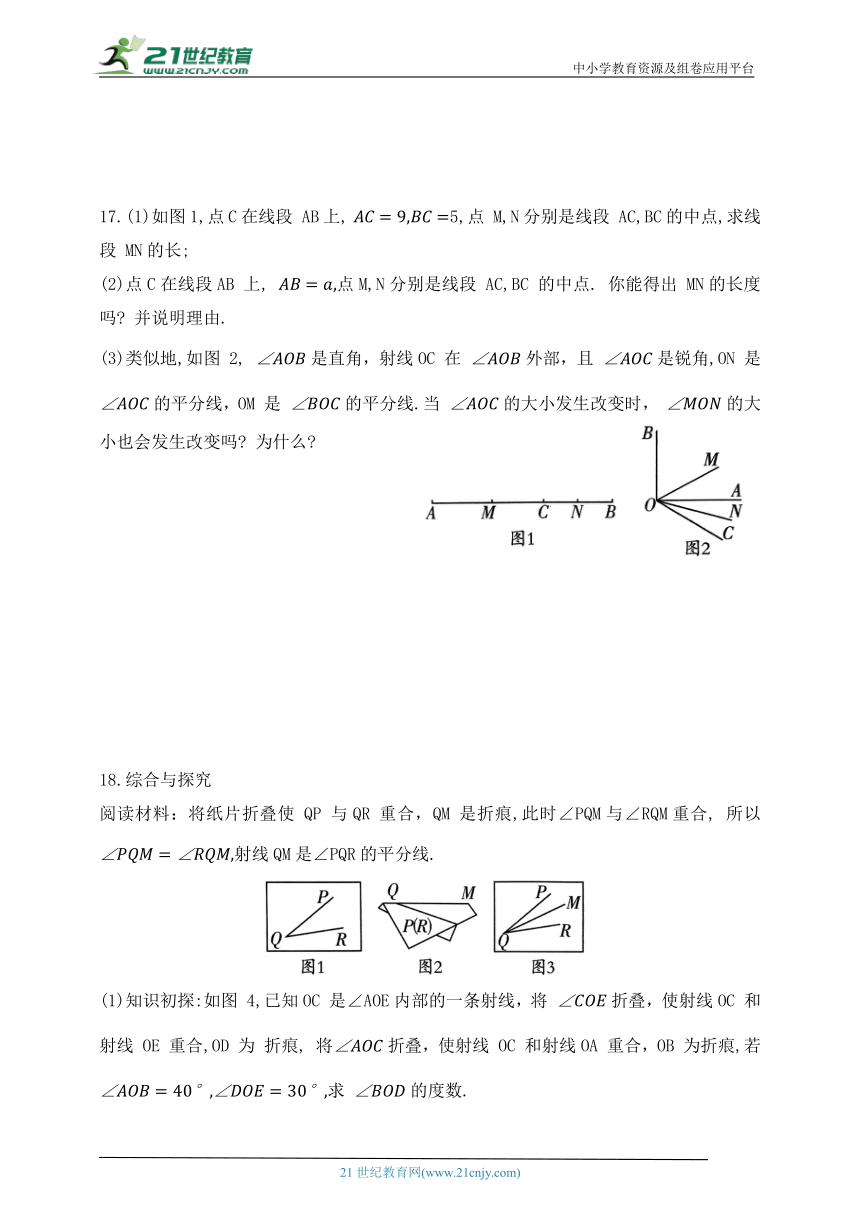
17.(1)如图1,点C在线段 AB上, 5,点 M,N分别是线段 AC,BC的中点,求线段 MN的长;
(2)点C在线段AB 上, 点M,N分别是线段 AC,BC 的中点. 你能得出 MN的长度吗 并说明理由.
(3)类似地,如图 2, 是直角,射线OC 在 外部,且 是锐角,ON 是 的平分线,OM 是 的平分线.当 的大小发生改变时, 的大小也会发生改变吗 为什么
18.综合与探究
阅读材料:将纸片折叠使 QP 与QR 重合,QM 是折痕,此时∠PQM与∠RQM重合, 所以 射线QM是∠PQR的平分线.
(1)知识初探:如图 4,已知OC 是∠AOE内部的一条射线,将 折叠,使射线OC 和射线 OE 重合,OD 为 折痕, 将折叠,使射线 OC 和射线OA 重合,OB 为折痕,若 求 的度数.
(2)类比探究:如图5,在长方形纸片ABCD中,点 E,F 分别在边 AB,AD 上,连接EF,将 折叠,使点 A 落在点 G 处, EH 平分 若 求 的度数(用含 α的式子表示).
参考答案
1. D 2. C 3. D 4. B 5. A 6. C 7. C 8. C
9.30°
12.40 解析:设∠MOC=β,∠CON=α,
因为ON 是∠BOC的平分线,所以∠BON=∠CON=α,所以∠BOM=∠MOC+∠BOC=β+2a,
因为 OM 是∠AOB 的平分线,所以∠AOM=∠BOM=β+2a,∠MON=∠MOC+∠CON=α+β,
因为∠AOC=80°,所以∠AOM+∠MOC=β+2a+β=∠AOC,所以2(α+β)=80°,
所以∠MON=a+β=40°,即∠MON的大小等于40°.
13.10 或40
14.32°
15.解:(1)因为∠ACD=∠ECB=90°,所以∠ACD-∠ECD=∠ECB-∠ECD,
所以∠ACE=∠BCD.故答案为:=;
(2)因为∠DCE=40°,所以∠ACE=90°-40°=50°,
所以∠ACB=50°+90°=140°;
(3)∠ACB+∠DCE=180°,
理由如下:因为∠ACD=∠ECB=90°,所以∠ACD+∠DCE+∠DCB=180°,
所以∠ACB+∠DCE=180°.
16.解:(1)因为∠AOC=30°,∠COD是直角,
所以∠BOC=180°-∠AOC=150°,∠COD=90°,
所以∠DOB=180°-∠AOC-∠COD=60°,
因为OE平分∠BOC,所以
理由如下:
设∠AOC=α,所以∠BOC=180°-∠AOC=180°-α,
因为∠COD是直角,所以∠COD=90°,
因为OE平分∠BOC,所以
所以∠DOE=90°-∠COE=90°-((90°-
即
17.解:(1)因为点 M,N分别是线段 AC,BC的中点,
所以
所以
(2)MN的长度是 理由如下:
由(1)知
所以
(3)不会发生变化,理由如下:
因为 ON 是∠AOC 的平分线,OM 是∠BOC的平分线,
所以
所以
所以当∠AOC的大小发生改变时,∠MON的大小不发生改变.
18.解:(1)由折叠可知,OD 是∠COE 的平分线, OB是∠AOC 的平分线,
所以∠DOC=∠DOE=30°,∠BOC=∠AOB=40°,
所以∠BOD=∠DOC+∠BOC=30°+40°=70°;
(2)由折叠可知,EF是∠AEG的平分线,所以∠AEF=∠FEG,
设∠AEF=∠FEG=β,
因为∠GEH=α,所以∠FEH=∠FEG+∠GEH=α+β,
因为 EH平分∠FEB,所以∠BEF=2∠FEH=2(α+β),
所以∠AEF+∠BEF=β+2(α+β)=180°,所以
即
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 基本平面图形
4 角的比较
1.若∠1=75°24',∠2=75.3°,∠3=75.12°, 则 ( )
A.∠1=∠2 B.∠2=∠3 C.∠1=∠3 D.以上都不对
2. 如图, ∠AOB = ∠COD, 则∠AOC 与∠DOB 的大小关系是 ( )
A.∠AOC>∠DOB B.∠AOC<∠DOB
C.∠AOC=∠DOB D.∠AOC与∠DOB无法比较大小
3.只利用一副(两块)三角尺不能直接拼出的角度是 ( )
A.75° B.105° C.150° D.165°
4.如图,OC 为∠AOB 内的一条射线,下列条件中不能确定OC平分∠AOB 的是( )
A.∠AOC=∠BOC B.∠AOC+∠COB=∠AOB C.∠AOB=2∠BOC
第4 题图 第5 题图
5.在学习角的过程中,小丽将一副三角板的直角顶点重合放置于A 处,然后将两块三角板在同一平面内绕着点 A 自由转动,她发现在转动的过程中∠CAD和∠BAE的和始终保持不变.则下列结论正确的是 ( )
6.如图,直线 AB,CD 相交于点O, OF 平分 若 则的度数为 ( )
第 6 题图 第 7题图
7.如图,点O为直线 AB 上一点,∠COD=90°,OE平分∠AOC,OG平分∠BOC,OF平分∠BOD,下列结论:①∠EOG=90°②∠DOE+∠BOF=180°③∠AOC-∠BOD= 90° ④∠DOG= 其中正确的有 ( )
A.①②③ B. ①②④ C.①③④ D.①②③④
8.如图, OC 平分 下列四个等式中正确的是 ( )
① ②∠DOC=2∠BOC ③ ④∠COD=3∠COB
A.①② B. ②③ C.③④ D.①④
9.如图,点O在直线 AB 上,OM 平分∠AOC,ON 平分∠BOC, 如果∠COM=2∠CON,则∠CON的度数为__________.
第9题图 第 10题图
10.如图,∠AOB=120°,∠BOC=30°,OD 是∠AOC的平分线,则∠BOD=__________.
11.已知一副三角板如图摆放,两个直角有公共的顶点,∠α=47°42',则∠β=___________(用度,分表示).
第 11题图 第 12题图
12.如图,OM 是∠AOB 的平分线,射线OC 在∠BOM 内部,ON 是∠BOC的平分线,已知 ∠AOC=80°,那么∠MON的大小等于__________°.
13.已知∠AOB=50°,由定点O引一条射线,使得∠BOC=30°,OM,ON 分别是∠AOB 和 ∠BOC 的平分线,则∠MON=__________°.
14.将三角板COD的直角顶点O 放置在直线AB 上(如图),若∠AOC=64°,射线 OE 平分 ∠BOC,则∠DOE的大小为___________.
15.如图,将两块直角三角板的直角顶点 C 叠放在一起.
(1)比较大小:∠ACE ______∠BCD;(填“>”“=”或“<”)
(2)若∠DCE=40°,求∠ACB的度数;
(3)猜想∠ACB 与∠DCE的数量关系,并说明理由.
16.已知点O是直线 AB 上的 一 点,∠COD 是 直角, OE 平分∠BOC.
(1) 如图 1,若∠AOC=30°,求∠COE,∠DOB的度数;
(2)将图 1 中的∠COD绕顶点O 顺时针旋转至图2 的位置,探究∠AOC 与∠DOE的度数之间的数量关系,并说明理由.
17.(1)如图1,点C在线段 AB上, 5,点 M,N分别是线段 AC,BC的中点,求线段 MN的长;
(2)点C在线段AB 上, 点M,N分别是线段 AC,BC 的中点. 你能得出 MN的长度吗 并说明理由.
(3)类似地,如图 2, 是直角,射线OC 在 外部,且 是锐角,ON 是 的平分线,OM 是 的平分线.当 的大小发生改变时, 的大小也会发生改变吗 为什么
18.综合与探究
阅读材料:将纸片折叠使 QP 与QR 重合,QM 是折痕,此时∠PQM与∠RQM重合, 所以 射线QM是∠PQR的平分线.
(1)知识初探:如图 4,已知OC 是∠AOE内部的一条射线,将 折叠,使射线OC 和射线 OE 重合,OD 为 折痕, 将折叠,使射线 OC 和射线OA 重合,OB 为折痕,若 求 的度数.
(2)类比探究:如图5,在长方形纸片ABCD中,点 E,F 分别在边 AB,AD 上,连接EF,将 折叠,使点 A 落在点 G 处, EH 平分 若 求 的度数(用含 α的式子表示).
参考答案
1. D 2. C 3. D 4. B 5. A 6. C 7. C 8. C
9.30°
12.40 解析:设∠MOC=β,∠CON=α,
因为ON 是∠BOC的平分线,所以∠BON=∠CON=α,所以∠BOM=∠MOC+∠BOC=β+2a,
因为 OM 是∠AOB 的平分线,所以∠AOM=∠BOM=β+2a,∠MON=∠MOC+∠CON=α+β,
因为∠AOC=80°,所以∠AOM+∠MOC=β+2a+β=∠AOC,所以2(α+β)=80°,
所以∠MON=a+β=40°,即∠MON的大小等于40°.
13.10 或40
14.32°
15.解:(1)因为∠ACD=∠ECB=90°,所以∠ACD-∠ECD=∠ECB-∠ECD,
所以∠ACE=∠BCD.故答案为:=;
(2)因为∠DCE=40°,所以∠ACE=90°-40°=50°,
所以∠ACB=50°+90°=140°;
(3)∠ACB+∠DCE=180°,
理由如下:因为∠ACD=∠ECB=90°,所以∠ACD+∠DCE+∠DCB=180°,
所以∠ACB+∠DCE=180°.
16.解:(1)因为∠AOC=30°,∠COD是直角,
所以∠BOC=180°-∠AOC=150°,∠COD=90°,
所以∠DOB=180°-∠AOC-∠COD=60°,
因为OE平分∠BOC,所以
理由如下:
设∠AOC=α,所以∠BOC=180°-∠AOC=180°-α,
因为∠COD是直角,所以∠COD=90°,
因为OE平分∠BOC,所以
所以∠DOE=90°-∠COE=90°-((90°-
即
17.解:(1)因为点 M,N分别是线段 AC,BC的中点,
所以
所以
(2)MN的长度是 理由如下:
由(1)知
所以
(3)不会发生变化,理由如下:
因为 ON 是∠AOC 的平分线,OM 是∠BOC的平分线,
所以
所以
所以当∠AOC的大小发生改变时,∠MON的大小不发生改变.
18.解:(1)由折叠可知,OD 是∠COE 的平分线, OB是∠AOC 的平分线,
所以∠DOC=∠DOE=30°,∠BOC=∠AOB=40°,
所以∠BOD=∠DOC+∠BOC=30°+40°=70°;
(2)由折叠可知,EF是∠AEG的平分线,所以∠AEF=∠FEG,
设∠AEF=∠FEG=β,
因为∠GEH=α,所以∠FEH=∠FEG+∠GEH=α+β,
因为 EH平分∠FEB,所以∠BEF=2∠FEH=2(α+β),
所以∠AEF+∠BEF=β+2(α+β)=180°,所以
即
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
