(预习衔接讲义)第三单元第5课时圆锥的认识(高频考点+典题精练)-2023-2024学年六年级下册数学高频易错尖子生培优(人教版)(含解析)
文档属性
| 名称 | (预习衔接讲义)第三单元第5课时圆锥的认识(高频考点+典题精练)-2023-2024学年六年级下册数学高频易错尖子生培优(人教版)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 120.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-27 00:00:00 | ||
图片预览




文档简介
圆锥的认识
核心知识点
圆锥的特征
【知识点归纳】
圆锥是由一个底面和一个侧面两部分组成的,它的底面是一个圆,侧面是一个曲面.
关联知识点
圆柱的特征
【知识点归纳】
圆柱就是由两个大小相同的圆和一个侧面组成的.它的底面是完全相同的两个圆,侧面是一个曲面.
一.选择题(共6小题)
1.将如图所示的圆心角为90°的扇形纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(接缝粘贴部分忽略不计),则围成的圆锥形纸帽是( )
A. B. C. D.
2.一个直角三角形,以它的一条直角边为轴旋转一周,得到的几何体是( )
A.长方体 B.圆柱 C.圆锥 D.球
3.圆锥的侧面展开后是( )
A.长方形 B.扇形 C.圆形
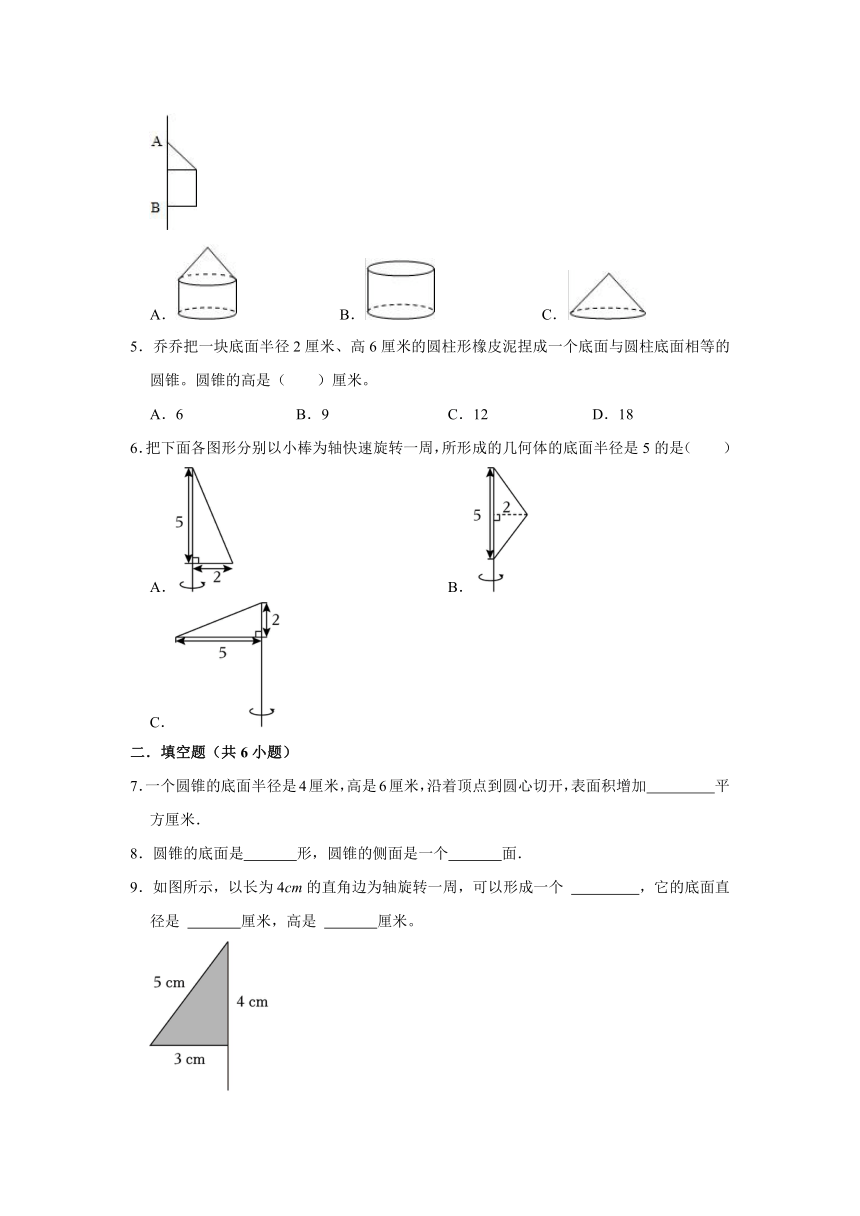
4.如图,以直线AB为轴旋转后会形成图形( )
A. B. C.
5.乔乔把一块底面半径2厘米、高6厘米的圆柱形橡皮泥捏成一个底面与圆柱底面相等的圆锥。圆锥的高是( )厘米。
A.6 B.9 C.12 D.18
6.把下面各图形分别以小棒为轴快速旋转一周,所形成的几何体的底面半径是5的是( )
A. B.
C.
二.填空题(共6小题)
7.一个圆锥的底面半径是4厘米,高是6厘米,沿着顶点到圆心切开,表面积增加 平方厘米.
8.圆锥的底面是 形,圆锥的侧面是一个 面.
9.如图所示,以长为4cm的直角边为轴旋转一周,可以形成一个 ,它的底面直径是 厘米,高是 厘米。
10.量得一个圆锥从顶点到底面圆周的距离是13cm,从顶点到底面圆心的距离是12cm,底面的直径是10cm,这个圆锥的高是 cm。
11.把一个圆锥沿底面直径切开(过顶点),切面是一个 形.
12.将一个底面直径为10厘米,高为6厘米的圆锥形木块沿底面直径分成形状、大小都相同的两半,表面积比原来增加了 平方厘米。
三.判断题(共7小题)
13.沿着一个直角三角形的任意一条边旋转一周,会得到一个圆锥.
14.从圆锥的顶点到底面周长上任一点的距离是圆锥的高. .
15.以直角三角形的一条边为轴旋转后形成的立体图形是圆柱. .
16.以直角三角形的最长边为轴旋转360度,会形成一个圆锥。
17.等腰三角形,绕任意一边旋转一周都不能形成圆锥.
18.圆锥的侧面展开后是一个等腰三角形. .
19.圆锥有无数条高,而圆柱只有一条高. .
四.应用题(共4小题)
20.如图是一个等腰直角三角形,将这个三角形以直角边AB为轴旋转一周,得到一个圆锥.圆锥的高和底面直径分别是多少厘米?
21.如图,在直角三角形ABC中,以AC所在的直线为轴旋转一周.
(1)可以得到一个什么图形?这个图形的高是多少?
(2)它的底面周长是多少?
22.如今自带帐篷旅游越来越受人们欢迎。如图,一种近似圆锥形帐篷的底面直径是5m,高是2.4m,这种圆锥形帐篷占地面积是多少?
23.将一个圆锥形纸筒沿一边剪开并展开(如图),已知圆锥的底面半径是5cm,它的底面周长是多少厘米?底面积是多少平方厘米?
圆锥的认识
参考答案与试题解析
一.选择题(共6小题)
1.【答案】B
【分析】圆锥的侧面展开后是扇形,由图可知:A、B一定重合,与A、B相邻的两个阴影一定在A所在的母线重合,而另一端一定与圆锥的底面相交,即靠近A、B两点的两个空白部分无法围成环并且紧贴底面;由此解答即可。
【解答】解将如图所示的圆心角为90°的扇形纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(接缝粘贴部分忽略不计),则围成的圆锥形纸帽是。
故选:B。
【点评】解答此题应认真观察,根据圆锥的特征进行分析、进而得出结论。
2.【答案】C
【分析】根据圆锥的展开图特点可知:直角三角形沿一条直角边旋转一周得到的几何体是一个圆锥,由此即可选择.
【解答】解:直角三角形沿一条直角边旋转一周得到的几何体是一个圆锥,
故选:C。
【点评】此题考查了圆锥的三视图的特点的灵活应用.
3.【答案】B
【分析】根据圆锥的特征:圆锥的侧面展开后是一个扇形,据此选择即可.
【解答】解:根据圆锥的特征可知:圆锥的侧面展开后是一个扇形;
故选:B.
【点评】此题考查了圆锥的侧面展开图,是对圆锥基础知识的掌握情况的了解,应注意平时基础知识的积累.
4.【答案】A
【分析】以直线AB为轴旋转后,得到的是立体图形上在是圆锥体,下面是圆柱体;据此解答.
【解答】解:以直线AB为轴旋转后,得到的是立体图形上在是圆锥体,下面是圆柱体;
故选:A.
【点评】此题考查了点、线、面、体,重在体现面动成体,考查学生立体图形的空间想象能力及分析问题、解决问题的能力.
5.【答案】D
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱和圆锥的体积相等、底面积相等时,圆锥的高是圆柱高的3倍,据此解答。
【解答】解:6×3=18(厘米)
答:圆锥的高是18厘米。
故选:D。
【点评】此题主要考查等底等高的圆柱和圆锥体积之间关系的灵活运用。
6.【答案】C
【分析】直角三角形旋转绕直角边旋转一周可以得到圆锥体,轴为圆锥的高,另一条直角边为半径,据此解答。
【解答】解:旋转一周可以得到圆锥,圆锥的高是2,底面半径是5。
故选:C。
【点评】本题考查了图形的旋转,关键理解旋转形成的图形的样子。
二.填空题(共6小题)
7.【答案】见试题解答内容
【分析】沿着顶点到圆心切开,即沿着圆锥的高切开,沿着高把这个圆锥切成大小相等的两部分,则表面积就增加了2个底为圆锥的底面直径、高为圆锥的高的三角形的面积;据此解答即可.
【解答】解:表面积增加:4×2×6÷2×2=48(平方厘米),
答:表面积增加48平方厘米.
故答案为:48.
【点评】沿着高把这个圆锥切成大小相等的两部分,则切割面是两个三角形,底是底面直径,高是圆锥的高.
8.【答案】见试题解答内容
【分析】根据圆锥的特征:圆锥的底面是一个圆,侧面是一个曲面,从顶点到底面圆心的距离叫做圆锥的高.
【解答】解:圆锥的底面是圆,侧面是一个曲面.
故答案为:圆,曲面.
【点评】此题主要考查圆锥的认识,目的是让学生牢固掌握圆锥的特征.
9.【答案】圆锥,6,4。
【分析】根据圆锥的定义:以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥,圆锥的底面半径是3厘米,高是4厘米,由此解答。
【解答】解:3×2=6(厘米)
因此以长为4cm的直角边为轴旋转一周,可以形成一个 圆锥,它的底面直径是6厘米,高是4厘米。
故答案为:圆锥,6,4。
【点评】本题考查了圆锥的特征。
10.【答案】12。
【分析】根据从圆锥的顶点到底面圆心的距离是圆锥的高,结合题意分析解答即可。
【解答】解:量得一个圆锥从顶点到底面圆周的距离是13cm,从顶点到底面圆心的距离是12cm,底面的直径是10cm,这个圆锥的高是12cm。
故答案为:12。
【点评】本题考查了圆锥的高的认识,结合题意分析解答即可。
11.【答案】见试题解答内容
【分析】把圆锥平行于底面进行切割,切面得到的是一个圆形;从圆锥的顶点向底面作垂直切割,得到的是一个以底面直径为底,以圆锥的高为高的等腰三角形,由此即可解答.
【解答】解:把一个圆锥沿底面直径切开(过顶点),切面是一个等腰三角形;
故答案为:等腰三角.
【点评】抓住圆锥的切割方法,从而得出切割面的特点,是解决本题的关键.
12.【答案】60。
【分析】根据题意,把圆锥形木块分成大小,形状完全相同的两部分,是按照圆锥的底面直径切开的,得到的是两个完全一样的等腰三角形,表面积增加的就是这两个切面三角形的面积之和,三角形的底是圆柱的底面直径,高是圆锥的高,据此利用三角形面积公式S=底×高÷2代入数字计算解答即可。
【解答】解:10×6÷2×2
=60÷2×2
=60(平方厘米)
答:表面积比原来增加了60平方厘米。
故答案为:60。
【点评】本题考查了圆锥的切面,切开后,表面积增加的是两个完全一样的等腰三角形的面积和。
三.判断题(共7小题)
13.【答案】见试题解答内容
【分析】以直角三角形的一条直角边为旋转轴旋转可得到一个圆锥,若以直角三角形的斜边为旋转轴旋转一周则会得到一个不规则的物体.
【解答】解:一个直角三角形沿着其中一条直角边旋转一周,得到的立体图形是一个以旋转的直角边为高,另一条直角边为底面半径的圆锥;
以直角三角形的斜边为旋转轴旋转一周则会得到一个不规则的物体,故题干说法是错误的.
故答案为:×.
【点评】解答此题的关键确定旋转图形的旋转轴,然后再确定旋转后得到的物体即可.
14.【答案】见试题解答内容
【分析】根据圆锥的高的含义:从圆锥的顶点到底面圆心的距离是圆锥的高,进而判断即可
【解答】解:从圆锥的顶点到底面周长上任一点的距离是圆锥的高,说法错误;
故答案为:×.
【点评】此题主要考查了圆锥的高的含义,应注意基础知识的积累.
15.【答案】见试题解答内容
【分析】如果以直角三角形的直角边为轴旋转一周后,得到的立体图形是一个圆锥,据此解答.
【解答】解:如果以直角三角形的直角边为轴旋转一周后,得到的立体图形是一个圆锥,
所以原题的说法错误.
故答案为:×.
【点评】此题考查的目的是理解掌握圆锥的特征.
16.【答案】×
【分析】以直角三角形的一条直角边为旋转轴旋转可得到一个圆锥,若以直角三角形的斜边为旋转轴旋转一周则会得到一个不规则的物体;据此解答。
【解答】解:以直角三角形的最长边为轴旋转360度,会得到一个不规则的物体,不会形成一个圆锥。
所以题干叙述错误。
故答案为:×。
【点评】解答此题的关键确定旋转图形的旋转轴,然后再确定旋转后得到的物体即可。
17.【答案】见试题解答内容
【分析】以直角三角形的一条直角边为旋转轴旋转可得到一个圆锥,而等腰直角三角形,绕一条直角边旋转一周能形成圆锥,据此解答.
【解答】解:以直角三角形的一条直角边为旋转轴旋转一周可得到一个圆锥,
所以等腰直角三角形,绕一条直角边旋转一周能形成圆锥,
因为等腰三角形包括等腰直角三角形,
所以题干叙述错误.
故答案为:×.
【点评】解答此题的关键确定旋转图形的旋转轴,然后再确定旋转后得到的物体即可.
18.【答案】见试题解答内容
【分析】因为用一个扇形和一个圆可以制作一个圆锥,扇形是圆锥的侧面,圆是底面,由此得出结论.
【解答】解:圆锥的侧面展开后是一个扇形,不是等腰三角形;
故答案为:×.
【点评】此题主要回顾圆锥的特征和制作过程,以此做出判断.
19.【答案】见试题解答内容
【分析】根据圆柱的特征:圆柱的上、下底面是完全相同的两个圆,侧面是一个曲面,侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高,圆柱有无数条高;
圆锥的特征是:圆锥的底面是一个圆,侧面是一个曲面,从圆锥的顶点到底面圆心的距离叫做圆锥的高,圆锥只有1条高.
【解答】解:圆柱的上、下底面之间的距离叫做圆柱的高,圆柱的高有无数条;
从圆锥的顶点到底面圆心的距离叫做圆锥的高,圆锥只有1条高;
所以上面的说法错误.
故答案为:×.
【点评】此题考查的目的是使学生掌握圆锥、圆柱的特征,理解圆锥和圆柱的高的意义.
四.应用题(共4小题)
20.【答案】见试题解答内容
【分析】如果以直角边AB为轴旋转一周,得到的是一个高为5cm,底面半径为5cm的圆锥,这个圆锥的底面直径是5×2=10(cm).
【解答】解:如果以直角边AB为轴旋转一周,
得到的是一个高为5cm,底面半径为5cm的圆锥,
这个圆锥的底面直径是:
5×2=10(cm)
答:圆锥的高是5cm,底面直径是10cm.
【点评】直角三形绕一直角边旋转一周可得到一个以旋转的直角边为旋转轴,另一直角边为底面半径的圆锥.
21.【答案】见试题解答内容
【分析】(1)直角三角形ABC中,以AC所在的直线为轴旋转一周,可以得到一个圆锥,这个图形的高是原三角形的高,即3cm;
(2)圆锥的底面是个圆,底面半径是原三角形的底,是2cm,所以底面周长是2×2×3.14=12.56厘米.
【解答】解:(1)可以得到一个圆锥,这个图形的高是3cm.
(2)2×2×3.14
=4×3.14
=12.56(cm)
答:它的底面周长是12.56厘米.
【点评】解答此题的关键是掌握圆锥的特征和面动成体的规律.
22.【答案】19.625平方米。
【分析】根据题意,求的是圆锥的底面积,运用圆的面积公式S=πr2,代入数据计算即可。
【解答】解:3.14×(5÷2)2
=3.14×6.25
=19.625(平方米)
答:这种圆锥形帐篷占地面积是19.625平方米。
【点评】此题主要考查圆的面积计算公式的灵活运用,结合题意分析解答即可。
23.【答案】底面周长是31.4厘米,底面积是78.5平方厘米。
【分析】首先根据C=2πr,求出底面周长,然后根据S=πr2求出底面积。
【解答】解:3.14×5×2=31.4(厘米)
3.14×52
=3.14×25
=78.5(平方厘米)
答:它的底面周长是31.4厘米,底面积是78.5平方厘米。
【点评】此题主要考查利用公式计算圆锥的底面周长和面积,关键是熟练掌握圆的周长和面积公式。
核心知识点
圆锥的特征
【知识点归纳】
圆锥是由一个底面和一个侧面两部分组成的,它的底面是一个圆,侧面是一个曲面.
关联知识点
圆柱的特征
【知识点归纳】
圆柱就是由两个大小相同的圆和一个侧面组成的.它的底面是完全相同的两个圆,侧面是一个曲面.
一.选择题(共6小题)
1.将如图所示的圆心角为90°的扇形纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(接缝粘贴部分忽略不计),则围成的圆锥形纸帽是( )
A. B. C. D.
2.一个直角三角形,以它的一条直角边为轴旋转一周,得到的几何体是( )
A.长方体 B.圆柱 C.圆锥 D.球
3.圆锥的侧面展开后是( )
A.长方形 B.扇形 C.圆形
4.如图,以直线AB为轴旋转后会形成图形( )
A. B. C.
5.乔乔把一块底面半径2厘米、高6厘米的圆柱形橡皮泥捏成一个底面与圆柱底面相等的圆锥。圆锥的高是( )厘米。
A.6 B.9 C.12 D.18
6.把下面各图形分别以小棒为轴快速旋转一周,所形成的几何体的底面半径是5的是( )
A. B.
C.
二.填空题(共6小题)
7.一个圆锥的底面半径是4厘米,高是6厘米,沿着顶点到圆心切开,表面积增加 平方厘米.
8.圆锥的底面是 形,圆锥的侧面是一个 面.
9.如图所示,以长为4cm的直角边为轴旋转一周,可以形成一个 ,它的底面直径是 厘米,高是 厘米。
10.量得一个圆锥从顶点到底面圆周的距离是13cm,从顶点到底面圆心的距离是12cm,底面的直径是10cm,这个圆锥的高是 cm。
11.把一个圆锥沿底面直径切开(过顶点),切面是一个 形.
12.将一个底面直径为10厘米,高为6厘米的圆锥形木块沿底面直径分成形状、大小都相同的两半,表面积比原来增加了 平方厘米。
三.判断题(共7小题)
13.沿着一个直角三角形的任意一条边旋转一周,会得到一个圆锥.
14.从圆锥的顶点到底面周长上任一点的距离是圆锥的高. .
15.以直角三角形的一条边为轴旋转后形成的立体图形是圆柱. .
16.以直角三角形的最长边为轴旋转360度,会形成一个圆锥。
17.等腰三角形,绕任意一边旋转一周都不能形成圆锥.
18.圆锥的侧面展开后是一个等腰三角形. .
19.圆锥有无数条高,而圆柱只有一条高. .
四.应用题(共4小题)
20.如图是一个等腰直角三角形,将这个三角形以直角边AB为轴旋转一周,得到一个圆锥.圆锥的高和底面直径分别是多少厘米?
21.如图,在直角三角形ABC中,以AC所在的直线为轴旋转一周.
(1)可以得到一个什么图形?这个图形的高是多少?
(2)它的底面周长是多少?
22.如今自带帐篷旅游越来越受人们欢迎。如图,一种近似圆锥形帐篷的底面直径是5m,高是2.4m,这种圆锥形帐篷占地面积是多少?
23.将一个圆锥形纸筒沿一边剪开并展开(如图),已知圆锥的底面半径是5cm,它的底面周长是多少厘米?底面积是多少平方厘米?
圆锥的认识
参考答案与试题解析
一.选择题(共6小题)
1.【答案】B
【分析】圆锥的侧面展开后是扇形,由图可知:A、B一定重合,与A、B相邻的两个阴影一定在A所在的母线重合,而另一端一定与圆锥的底面相交,即靠近A、B两点的两个空白部分无法围成环并且紧贴底面;由此解答即可。
【解答】解将如图所示的圆心角为90°的扇形纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(接缝粘贴部分忽略不计),则围成的圆锥形纸帽是。
故选:B。
【点评】解答此题应认真观察,根据圆锥的特征进行分析、进而得出结论。
2.【答案】C
【分析】根据圆锥的展开图特点可知:直角三角形沿一条直角边旋转一周得到的几何体是一个圆锥,由此即可选择.
【解答】解:直角三角形沿一条直角边旋转一周得到的几何体是一个圆锥,
故选:C。
【点评】此题考查了圆锥的三视图的特点的灵活应用.
3.【答案】B
【分析】根据圆锥的特征:圆锥的侧面展开后是一个扇形,据此选择即可.
【解答】解:根据圆锥的特征可知:圆锥的侧面展开后是一个扇形;
故选:B.
【点评】此题考查了圆锥的侧面展开图,是对圆锥基础知识的掌握情况的了解,应注意平时基础知识的积累.
4.【答案】A
【分析】以直线AB为轴旋转后,得到的是立体图形上在是圆锥体,下面是圆柱体;据此解答.
【解答】解:以直线AB为轴旋转后,得到的是立体图形上在是圆锥体,下面是圆柱体;
故选:A.
【点评】此题考查了点、线、面、体,重在体现面动成体,考查学生立体图形的空间想象能力及分析问题、解决问题的能力.
5.【答案】D
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱和圆锥的体积相等、底面积相等时,圆锥的高是圆柱高的3倍,据此解答。
【解答】解:6×3=18(厘米)
答:圆锥的高是18厘米。
故选:D。
【点评】此题主要考查等底等高的圆柱和圆锥体积之间关系的灵活运用。
6.【答案】C
【分析】直角三角形旋转绕直角边旋转一周可以得到圆锥体,轴为圆锥的高,另一条直角边为半径,据此解答。
【解答】解:旋转一周可以得到圆锥,圆锥的高是2,底面半径是5。
故选:C。
【点评】本题考查了图形的旋转,关键理解旋转形成的图形的样子。
二.填空题(共6小题)
7.【答案】见试题解答内容
【分析】沿着顶点到圆心切开,即沿着圆锥的高切开,沿着高把这个圆锥切成大小相等的两部分,则表面积就增加了2个底为圆锥的底面直径、高为圆锥的高的三角形的面积;据此解答即可.
【解答】解:表面积增加:4×2×6÷2×2=48(平方厘米),
答:表面积增加48平方厘米.
故答案为:48.
【点评】沿着高把这个圆锥切成大小相等的两部分,则切割面是两个三角形,底是底面直径,高是圆锥的高.
8.【答案】见试题解答内容
【分析】根据圆锥的特征:圆锥的底面是一个圆,侧面是一个曲面,从顶点到底面圆心的距离叫做圆锥的高.
【解答】解:圆锥的底面是圆,侧面是一个曲面.
故答案为:圆,曲面.
【点评】此题主要考查圆锥的认识,目的是让学生牢固掌握圆锥的特征.
9.【答案】圆锥,6,4。
【分析】根据圆锥的定义:以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥,圆锥的底面半径是3厘米,高是4厘米,由此解答。
【解答】解:3×2=6(厘米)
因此以长为4cm的直角边为轴旋转一周,可以形成一个 圆锥,它的底面直径是6厘米,高是4厘米。
故答案为:圆锥,6,4。
【点评】本题考查了圆锥的特征。
10.【答案】12。
【分析】根据从圆锥的顶点到底面圆心的距离是圆锥的高,结合题意分析解答即可。
【解答】解:量得一个圆锥从顶点到底面圆周的距离是13cm,从顶点到底面圆心的距离是12cm,底面的直径是10cm,这个圆锥的高是12cm。
故答案为:12。
【点评】本题考查了圆锥的高的认识,结合题意分析解答即可。
11.【答案】见试题解答内容
【分析】把圆锥平行于底面进行切割,切面得到的是一个圆形;从圆锥的顶点向底面作垂直切割,得到的是一个以底面直径为底,以圆锥的高为高的等腰三角形,由此即可解答.
【解答】解:把一个圆锥沿底面直径切开(过顶点),切面是一个等腰三角形;
故答案为:等腰三角.
【点评】抓住圆锥的切割方法,从而得出切割面的特点,是解决本题的关键.
12.【答案】60。
【分析】根据题意,把圆锥形木块分成大小,形状完全相同的两部分,是按照圆锥的底面直径切开的,得到的是两个完全一样的等腰三角形,表面积增加的就是这两个切面三角形的面积之和,三角形的底是圆柱的底面直径,高是圆锥的高,据此利用三角形面积公式S=底×高÷2代入数字计算解答即可。
【解答】解:10×6÷2×2
=60÷2×2
=60(平方厘米)
答:表面积比原来增加了60平方厘米。
故答案为:60。
【点评】本题考查了圆锥的切面,切开后,表面积增加的是两个完全一样的等腰三角形的面积和。
三.判断题(共7小题)
13.【答案】见试题解答内容
【分析】以直角三角形的一条直角边为旋转轴旋转可得到一个圆锥,若以直角三角形的斜边为旋转轴旋转一周则会得到一个不规则的物体.
【解答】解:一个直角三角形沿着其中一条直角边旋转一周,得到的立体图形是一个以旋转的直角边为高,另一条直角边为底面半径的圆锥;
以直角三角形的斜边为旋转轴旋转一周则会得到一个不规则的物体,故题干说法是错误的.
故答案为:×.
【点评】解答此题的关键确定旋转图形的旋转轴,然后再确定旋转后得到的物体即可.
14.【答案】见试题解答内容
【分析】根据圆锥的高的含义:从圆锥的顶点到底面圆心的距离是圆锥的高,进而判断即可
【解答】解:从圆锥的顶点到底面周长上任一点的距离是圆锥的高,说法错误;
故答案为:×.
【点评】此题主要考查了圆锥的高的含义,应注意基础知识的积累.
15.【答案】见试题解答内容
【分析】如果以直角三角形的直角边为轴旋转一周后,得到的立体图形是一个圆锥,据此解答.
【解答】解:如果以直角三角形的直角边为轴旋转一周后,得到的立体图形是一个圆锥,
所以原题的说法错误.
故答案为:×.
【点评】此题考查的目的是理解掌握圆锥的特征.
16.【答案】×
【分析】以直角三角形的一条直角边为旋转轴旋转可得到一个圆锥,若以直角三角形的斜边为旋转轴旋转一周则会得到一个不规则的物体;据此解答。
【解答】解:以直角三角形的最长边为轴旋转360度,会得到一个不规则的物体,不会形成一个圆锥。
所以题干叙述错误。
故答案为:×。
【点评】解答此题的关键确定旋转图形的旋转轴,然后再确定旋转后得到的物体即可。
17.【答案】见试题解答内容
【分析】以直角三角形的一条直角边为旋转轴旋转可得到一个圆锥,而等腰直角三角形,绕一条直角边旋转一周能形成圆锥,据此解答.
【解答】解:以直角三角形的一条直角边为旋转轴旋转一周可得到一个圆锥,
所以等腰直角三角形,绕一条直角边旋转一周能形成圆锥,
因为等腰三角形包括等腰直角三角形,
所以题干叙述错误.
故答案为:×.
【点评】解答此题的关键确定旋转图形的旋转轴,然后再确定旋转后得到的物体即可.
18.【答案】见试题解答内容
【分析】因为用一个扇形和一个圆可以制作一个圆锥,扇形是圆锥的侧面,圆是底面,由此得出结论.
【解答】解:圆锥的侧面展开后是一个扇形,不是等腰三角形;
故答案为:×.
【点评】此题主要回顾圆锥的特征和制作过程,以此做出判断.
19.【答案】见试题解答内容
【分析】根据圆柱的特征:圆柱的上、下底面是完全相同的两个圆,侧面是一个曲面,侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高,圆柱有无数条高;
圆锥的特征是:圆锥的底面是一个圆,侧面是一个曲面,从圆锥的顶点到底面圆心的距离叫做圆锥的高,圆锥只有1条高.
【解答】解:圆柱的上、下底面之间的距离叫做圆柱的高,圆柱的高有无数条;
从圆锥的顶点到底面圆心的距离叫做圆锥的高,圆锥只有1条高;
所以上面的说法错误.
故答案为:×.
【点评】此题考查的目的是使学生掌握圆锥、圆柱的特征,理解圆锥和圆柱的高的意义.
四.应用题(共4小题)
20.【答案】见试题解答内容
【分析】如果以直角边AB为轴旋转一周,得到的是一个高为5cm,底面半径为5cm的圆锥,这个圆锥的底面直径是5×2=10(cm).
【解答】解:如果以直角边AB为轴旋转一周,
得到的是一个高为5cm,底面半径为5cm的圆锥,
这个圆锥的底面直径是:
5×2=10(cm)
答:圆锥的高是5cm,底面直径是10cm.
【点评】直角三形绕一直角边旋转一周可得到一个以旋转的直角边为旋转轴,另一直角边为底面半径的圆锥.
21.【答案】见试题解答内容
【分析】(1)直角三角形ABC中,以AC所在的直线为轴旋转一周,可以得到一个圆锥,这个图形的高是原三角形的高,即3cm;
(2)圆锥的底面是个圆,底面半径是原三角形的底,是2cm,所以底面周长是2×2×3.14=12.56厘米.
【解答】解:(1)可以得到一个圆锥,这个图形的高是3cm.
(2)2×2×3.14
=4×3.14
=12.56(cm)
答:它的底面周长是12.56厘米.
【点评】解答此题的关键是掌握圆锥的特征和面动成体的规律.
22.【答案】19.625平方米。
【分析】根据题意,求的是圆锥的底面积,运用圆的面积公式S=πr2,代入数据计算即可。
【解答】解:3.14×(5÷2)2
=3.14×6.25
=19.625(平方米)
答:这种圆锥形帐篷占地面积是19.625平方米。
【点评】此题主要考查圆的面积计算公式的灵活运用,结合题意分析解答即可。
23.【答案】底面周长是31.4厘米,底面积是78.5平方厘米。
【分析】首先根据C=2πr,求出底面周长,然后根据S=πr2求出底面积。
【解答】解:3.14×5×2=31.4(厘米)
3.14×52
=3.14×25
=78.5(平方厘米)
答:它的底面周长是31.4厘米,底面积是78.5平方厘米。
【点评】此题主要考查利用公式计算圆锥的底面周长和面积,关键是熟练掌握圆的周长和面积公式。
