(预习衔接讲义)第四单元第5课时正比例(高频考点+典题精练)-2023-2024学年六年级下册数学高频易错尖子生培优(人教版)(含解析)
文档属性
| 名称 | (预习衔接讲义)第四单元第5课时正比例(高频考点+典题精练)-2023-2024学年六年级下册数学高频易错尖子生培优(人教版)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 339.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-27 18:43:13 | ||
图片预览




文档简介
第四单元第5课时正比例
核心知识点
1.正比例和反比例的意义
【知识点归纳】
1.正比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.如果用字母x和y表示这两种相关联的量,用k表示它们的比值(一定),正比例关系可以用式子表示为:=k(一定).
2.反比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系.如果用字母x和y表示这两种相关联的量,用k表示它们的乘积(一定),反比例的关系可以表示为:xy=k(一定).
2.正比例
【知识点归纳】
正比例,简称正比,是指两种相关联的量,一种量变化,另一种量也随着变化。如果这两种量中相对应的两个数比值(或者说商)一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。
关联知识点
3.解比例
【知识点归纳】
根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项.求比例中的未知项,叫做解比例.
一般来说,求比例的未知项有以下两种情况:
(1)求未知外项=
(2)求未知内项=
一.选择题(共10小题)
1.如图表示两辆汽车所行驶的路程与相应时间关系的图象,下列关于图象描述错误的是( )
A.两辆汽车行驶的路程和时间都成正比例
B.从昆明到大理大约有350千米,甲车从昆明到大理大约要4个小时
C.从图象上看甲车的速度比乙车快
D.从图象上看乙车的速度比甲车快
2.学习下列哪个知识时不是运用了数形结合的方法?( )
A.小数乘法 B.正比例图像
C.折线统计图
3.下面各题中的两种量成正比例关系的有( )个.
①比例尺一定,两地的实际距离和图上距离;②如果y=5x,y和x;③圆的面积和直径;④订阅《小学生作文》的份数和总价;⑤书的总册数一定,每包的册数和包数;⑥大树的高度和大树影子的长度.
A.2 B.3 C.4 D.5
4.每平方米种植玉米的棵数一定,土地的面积和种植玉米的总棵数( )
A.成正比例 B.成反比例 C.不成比例
5.如果5a=3b,那么a和b( )关系.
A.成正比例 B.成反比例 C.不成比例
6.图中,( )表示的两个量成正比例关系。
A. B.
C. D.
7.如图中,表示正比例图象的是( )
A. B. C. D.
8.下面关系式,( )中x与y不成正比例(x、y均不为零).
A.x×=3 B.5x=6y C.4÷x=y D.x=y
9.下列图象表示正比例关系的是( )
A. B.
C. D.
10.圆柱的体积一定,底面积和高( )
A.成正比例 B.成反比例 C.不成比例
二.填空题(共10小题)
11.如表所示,当x和y成反比例时,空格里应填 ;当x和y成正比例时,空格里应填 。
x 6 2
y 12
12.如果x与y成正比例关系,下表中的“?”处应该是 ;如果x与y成反比例关系,右表中的“?”处应该是 。
x 180 ?
y 60 50
13.观察表格,如果x与y成正比例,那么m的值为 ;如果x与y成反比例,那么的值为 。
x 4 m
y 6 8
14.如下表,当x,y成正比例时,a的值是 ;当x、y成反比例时,a的值是 。
x 6 3
y 2 a
15.下表中x和y两个量成正比例,请把表格填写完整。
x 6 2.5
y 3 4 3.6
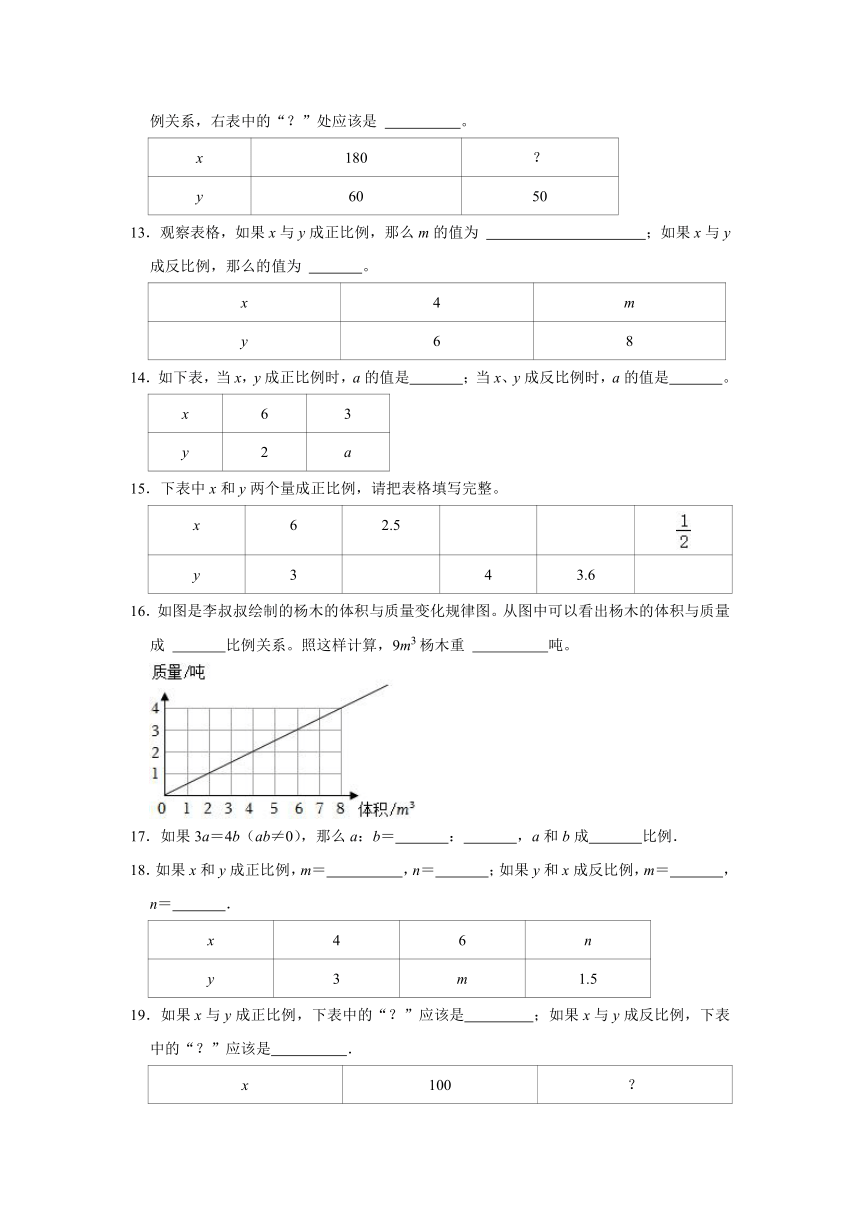
16.如图是李叔叔绘制的杨木的体积与质量变化规律图。从图中可以看出杨木的体积与质量成 比例关系。照这样计算,9m3杨木重 吨。
17.如果3a=4b(ab≠0),那么a:b= : ,a和b成 比例.
18.如果x和y成正比例,m= ,n= ;如果y和x成反比例,m= ,n= .
x 4 6 n
y 3 m 1.5
19.如果x与y成正比例,下表中的“?”应该是 ;如果x与y成反比例,下表中的“?”应该是 .
x 100 ?
y 80 40
20.观察如表:如果x和y成正比例,那么a等于 ;如果x和y成反比例,那么a等于 。
x 2 8
y 16 a
三.判断题(共10小题)
21.如果a÷2=b,且a、b≠0,那么a、b成正比例. .
22.在同一幅地图上,图上距离越大实际距离就越大. .
23.一根电线,用去的米数与剩下的米数成反比例. .
24.人的身高和体重成正比例. .
25.长方形的长一定,它的宽与面积成 比例.
26.m﹣n=0,m、n均不为0,m和n成正比例. .
27.长方形的周长一定时,长和宽成反比例. .
28.ab﹣8=17.25,则a和b不成比例 .
29.长方体一个面的面积和它的表面积成正比. .
30.长方形的面积一定,长和宽成正比例. .
四.应用题(共11小题)
31.在一次自行车越野赛中,小明骑车的时间与路程如下表.
时间(分) 8 10 20 40 60
路程(千米) 2 2.5 5 10 15
(1)路程和时间成什么比例?
(2)时间、路程和速度这三种量,在什么情况下成正比例,什么情况下成反比例?说明理由.
32.淘淘家在装修房屋时,买了同样大小的地板砖,铺地面积与所需块数的关系如图.他家的客厅面积是36m2,需要铺多少块这样的地板砖?(用比例解决问题)
33.平行四边形的高是3cm,先填表,再根据表中的数据回答问题.
底/cm 8 10 20 30
面积/cm2 24 90
(1)表中平行四边形的底和面积是 的量,平行四边形的 随着 的变化而变化.
(2)写出几组这两种量中相对应的两个数的比,求出比值,并比较比值的大小.
(3)上面求出的比值表示的意义是什么?
(4)表中相关联的两种量成正比例吗?为什么?
34.汽车数量与运货质量的数据如下表,根据表中的数据回答下面各题.
汽车数量/辆 1 2 3 4 5 6 7
运货质量/吨 4 8 12 16 20 24 28
(1)表中 和 是两种相关联的量, 随着 的变化而变化.
(2)写出几组这两种量中相对应的两个数的比,求出比值,并比较比值的大小.
(3)上面求出的比值表示的意义是什么?
(4)表中相关联的两种量成正比例吗?为什么?
35.食堂有一批大米.如表记录的是每天的用量和所用的天数.
每天的用量/kg 40 25 5
所用的天数 8 10 20 80
(1)把上表填写完整.
(2)每天的用量和所用的天数成反比例吗?为什么?
(3)如果每天用8kg,那么可以用多少天?
(4)如果计划用100天,那么每天应该用多少千克?
36.如图图象表示实验小学食堂的用煤天数和用煤量的关系.
(1)实验小学食堂用煤的天数和用煤量是否成正比例?
(2)根据图象判断,食堂5天要用煤多少吨?2.4吨煤可以用多少天?
37.下图表示一根水管不停地向水箱内注水时,水箱内水的体积的变化情况.
(1)水箱内水的体积与注水的时间成正比例吗?为什么?
(2)利用图象估一估,10分能注水多少升?注水45升需要多少分?再实际计算一下.
38.
时间/时 1 2 3 4 5 6 …
路程/千米 90 …
①先把上表补充完整,再根据表中的数据,在图中描出时间和路程的对应点,再把这些点按顺序连起来.
②时间和路程成 比例,理由是 .
③利用图象估计一下,2.5时行 千米,行675千米需要 小时.
39.如图中线段AB表示一辆汽车行驶的路程与时间的关系.
①这辆汽车行驶了多长时间?行驶了多少千米?
②这辆汽车2.5小时行驶了多少千米?
③这辆汽车行驶900km要多长时间?
40.根据甲、乙两车的行程图,回答下面的问题.
(1)甲、乙两车行驶的路程与时间是否成比例?说说理由.
(2)哪一辆汽车的行驶速度快些?
41.如图,甲、乙两车运货的吨数与次数的关系如图.
(1)甲车的运货量与运货次数成什么比例关系?乙车呢?
(2)甲、乙两车各运货6次,运货量相差多少吨?
第四单元第5课时正比例
参考答案与试题解析
一.选择题(共10小题)
1.【答案】D
【分析】根据图像都是直线可以判断两辆汽车行驶的路程和时间都成正比例,再根据两车行驶360千米所用的时间确定两车速度的快慢即可。
【解答】解:从图像中可以得到:
(1)两辆汽车形式的路程与时间的关系图像都是一条直线,所以两辆汽车行驶的路程和时间都成正比例。
(2)甲车4小时到达,乙车8小时到达,所以甲车的速度大于乙车的速度。
故选:D。
【点评】本题考查了正比例关系图像,要读懂图像反映出来的信息,并能根据信息解决问题。
2.【答案】A
【分析】小数乘法是一种计算,不需要图像;正比例图形和折线统计图都是图像(形)与数字的结合。
【解答】解:小数乘法是一种计算,不需要图像;正比例图形和折线统计图都是根据数据作图或根据图像(形)找数字信息或进行有关计算。
故选:A。
【点评】本题考查对小数乘法、正比例图像、折线统计图的理解。
3.【答案】B
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:①图上距离:实际距离=比例尺(一定),所以比例尺一定,图上距离和实际距离成正比例;
②y=5x,y:x=5(一定),所以x和y成正比例;
③圆的面积S=π(d÷2)2,=(一定),所以圆的面积与直径的平方成正比例,与直径不成比例;
④因为订阅《小学生作文》的总价÷份数=单价(一定),是订阅《小学生作文》的总价和份数的比值一定,
符合正比例的意义,所以订阅《小学生作文》的份数和总价成正比例;
⑤因为每包书的册数×包数=书的总册数(一定),所以每包数的册数和包数成反比例;
⑥同一时刻,同一地点物体的高度和影子的长度的比值一定,即物体的高度:影子的高度=比值(一定),所以同一时刻,同一地点物体的高度和影子的长度成正比例;本题没有说明同时同地,所以不成比例.
所以成正比例的有:①、②、④,3个.
故选:B.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
4.【答案】A
【分析】根据正反比例的意义,分析数量关系,找出一定的量,然后看那两个变量是比值一定还是乘积一定,从而判定成什么比例关系.
【解答】解:土地的面积和种植玉米的总棵数是两种相关联的量,它们与每平方米种植玉米的棵数有下面的关系:
种植玉米的总棵数:土地的面积=每平方米种植玉米的棵数(一定);
已知每平方米种植玉米的棵数一定,也就是土地的面积和种植玉米的总棵数的比值一定,所以土地的面积和种植玉米的总棵数成正比例.
故选:A.
【点评】此题重点考查正比例和反比例的意义.
5.【答案】A
【分析】先把等式变成a等于多少b,再根据正比例和反比例的意义求解.
【解答】解:5a=3b,
那么:a:b=;
是个定值,一个因数一定,积和另一个因数成正比例.
故选:A.
【点评】一个因数一定,积和另一个因数成正比例;积一定,两个因数成反比例.
6.【答案】D
【分析】要知道成正比例关系的图象特点是一条直线,相关联的两个量应是比值或商一定,反比例关系的图象是一条曲线,且一个量扩大、另一个量缩小;据此即可作出正确选择。
【解答】解:由图分析可知:
A.是一条曲折线,表示的两个量的乘积不一定,不成比例,不符合题意;
B.虽然是直线,但是表示的是一个量增加,而另一个量减少,不是比值或乘积一定,所以不成正比例,不符合题意;
C.是一条曲折线,表示的两个量的乘积不一定,不成比例,不符合题意;
D.是一条递增的直线,相对应的两个数据的比值一定,是正比例关系,符合题意。
故选:D。
【点评】本题是成正、反比例关系知识的拓展,是把数和形结合起来,研究两个相关联的量之间的关系。
7.【答案】B
【分析】根据正比例的意义是:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们之间的关系就是正比例关系,由此可知,正比例的图象是过原点的一条射线,据此解答。
【解答】解;根据正比例图象的特点可知,图B符合正比例图象的特点,所以图B是正比例图象。
故选:B。
【点评】此题考查的目的是理解掌握正比例的意义以及正比例图象的特点。
8.【答案】C
【分析】判断X与Y是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例.据此进行逐项分析再选择.
【解答】解:A、因为X×=3,则有=3(一定),是比值一定,所以X与Y成正比例;
B、因为5X=6Y,则有=(一定),是比值一定,所以X与Y成正比例;
C、因为4÷X=Y,则有XY=4(一定),是乘积一定,所以X与Y成反比例;
D、因为X=Y,则有=(一定),是比值一定,所以X与Y成正比例;
故选:C.
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量是否成正比例,就看这两种量是否是对应的比值一定,再做出判断.
9.【答案】C
【分析】成正比例关系的图象是经过原点的一条射线,据此回答即可.
【解答】解:选项A:不是过原点的一条射线,不成正比例关系,故错误;
选项B:不是过原点的一条射线,不成正比例关系,故错误;
选项C:是以原点为端点的一条射线,成正比例关系,故正确;
选项D:不是过原点的一条射线,不成正比例关系,故错误;
故选:C.
【点评】本题主要考查了成正比例关系的图象性质.
10.【答案】B
【分析】判定两种相关联的量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定就成反比例.
【解答】解:圆柱的底面积×高=体积(一定),是乘积一定,所以圆柱的底面积和高成反比例;
故选:B.
【点评】此题属于根据正、反比例的意义,判断两种相关联的量是成正比例还是成反比例,就看两种量是对应的比值一定,还是对应的乘积一定,再做出解答.
二.填空题(共10小题)
11.【答案】36;4。
【分析】两个相关联的量,若其比值一定,则两个量成正比例关系;若其乘积一定,则两个量成反比例关系。据此解答。
【解答】解:当x和y成反比例时,2y=6×12,解得y=36;
当x和y成正比例时,6:12=2:y,解得y=4。
故答案为:36;4。
【点评】本题考查利用比例的基本性质解比例。
12.【答案】150,216。
【分析】根据比例的基本性质,内项积等于外项积,据此把乘积式化为比例式;再根据两个相关联的量,若它们的比值一定,则它们成正比例;若它们的乘积一定,则它们成反比例。
【解答】解:x:50=180:60
x:50=3:1
x=50×3
x=150
50x=180×60
50x=10800
x=216
故答案为:150,216。
【点评】此题考查了解正比例和反比例的知识,要求学生掌握。
13.【答案】,3。
【分析】如果x与y成正比例,那么x与y的比值一定,如果x与y成反比例,那么x与y的乘积一定。
【解答】解:当x与y成正比例,
4:6=m:8
6m=32
m=
x与y成反比例,
8m=4×6
8m=24
m=3
故答案为:,3。
【点评】理解正比例和反比例的意义是解题关键。
14.【答案】1、4。
【分析】如果相关的两个量的比值一定,这两个量成正比例关系,如果相关的两个量的乘积一定,这两个量成反比例关系。
【解答】解:当x,y成正比例时,则=,解得a=1;
当x、y成反比例时,则6×2=3a,解得a=4。
所以当x,y成正比例时,a的值是1;当x、y成反比例时,a的值是4。
故答案为:1、4。
【点评】要熟知正比例和反比例的意义。
15.【答案】1.25,8,7.2,。
【分析】两个数成正比例,也就是x和y两个数的商不变,先求出这两个数的商,再根据被除数=除数×商,以及除数=被除数÷商即可解答。
【解答】解:6÷3=2
2.5÷2=1.25
4×2=8
3.6×2=7.2
÷2=
x 6 2.5 8 7.2
y 3 1.25 4 3.6
故答案为:1.25,8,7.2,。
【点评】此题主要考查学生对正比例的认识,以及利用正比例关系是解决问题的能力。
16.【答案】正、4.5。
【分析】比例图像是一条直线,所以杨木的体积与质量成正比例关系;根据图像可以看出,每m3杨木重0.5吨,据此求出9m3杨木的质量。
【解答】解:比例图像是一条直线,所以杨木的体积与质量成正比例关系。
9×0.5=4.5(吨)
答:9m3杨木重4.5吨。
故答案为:正、4.5。
【点评】本题考查了根据图像判断两种量成哪种比例关系及根据图像信息解决问题的能力。
17.【答案】见试题解答内容
【分析】根据比例的基本性质,两内项之积等于两外项之积,即可得解.
【解答】解:3a=4b,
a:b=4:3;
答:如果3a=4b,那么a:b=4:3,a和b成正比例.
故答案为:4,3,正.
【点评】两个相关联的量,它们的比值是固定值,则这两个量成正比例.
18.【答案】见试题解答内容
【分析】1.正比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.
2.反比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系.
然后根据比值一定,和乘积一定;列式解答即可.
【解答】解:如果x和y成正比例,m=6÷(4÷3)=4.5,
n=1.5×(4÷3)=2;
如果y和x成反比例,m=3×4÷6=2,
n=3×4÷1.5=8.
故答案为:4.5;2;2;8.
【点评】解答此题的关键是明白,两个数成正比例时,它们的商(比值)一定;成反比例时,它们的积一定.
19.【答案】见试题解答内容
【分析】(1)如果表中x和y成正比例,说明x和y对应的比值一定,根据两个比的比值相等列比例,并解比例即可;
(2)如果表中x和y成反比例,说明x和y对应的乘积一定,根据两个比的乘积相等列方程,并解方程即可.
【解答】解:
(1)100:80=x:40
80x=100×40
80x÷80=4000÷80
x=50
(2)40x=80×100
40x=8000
40x÷40=8000÷40,
x=200
故答案为:50,200.
【点评】此题主要考查了正比例和反比例的意义以及应用,要熟练掌握.
20.【答案】64,4。
【分析】成正比例就是两个量的比值一定,就是2:16=8:a,成反比例就是两个量的积一定,就是2×16=8a,计算即可解答。
【解答】解:2:16=8:a
2a=16×8
2a=128
a=64
2×16=8a
8a=32
a=4
答:如果x和y成正比例,那么a等于64,如果x和y成反比例,那么a等于 4。
故答案为:64,4。
【点评】本题考查的是正比例和反比例的意义,理解和运用正比例和反比例的意义是解答关键。
三.判断题(共10小题)
21.【答案】见试题解答内容
【分析】判断a与b是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例.
【解答】解:因为a÷2=b,且a、b≠0,
所以a÷b=2(一定),
即a与b的比值一定,
所以a、b成正比例,
故答案为:√.
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量是否成正比例,就看这两种量是否是对应的比值一定,再做出判断.
22.【答案】√
【分析】对的,因为比例尺相同,实际距离与图上距离成正比.
【解答】解:因为图上距离:实际距离=比例尺一定,
所以在同一幅地图上,图上距离与实际距离成正比例,
故在同一幅地图上,图上距离越大实际距离就越大.
故答案为:√.
【点评】本题结合比例尺考查了正比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.
23.【答案】见试题解答内容
【分析】①两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做成正比例关系.
②两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系.
③除了这两种情况,其余的都不成比例关系
【解答】解:用去的米数与剩下的米数相加是总米数,
它们与总量是加数、加数、和的关系,
它们的乘积不是一定的,比值也不是一定的.
所以用去的米数与剩下的米数不成任何比例关系.
故答案为:×.
【点评】此题重点考查辨识成正比例的量与成反比例的量.
24.【答案】×
【分析】判定两种相关联的量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定就成反比例;如果不是乘积或比值一定,就不成比例.
【解答】解:人的身高和体重虽是两种相关联的量,但是它们的乘积或比值都不一定,所以不成比例;
故答案为:×.
【点评】此题属于根据正、反比例的意义,判断两种相关联的量是成正比例还是成反比例,就看两种量是对应的比值一定,还是对应的乘积一定,再做出解答.
25.【答案】见试题解答内容
【分析】判断长方形的宽与面积成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例.
【解答】解:长方形的面积÷宽=长(一定),是比值一定,长方形的宽与面积成正比例.
故答案为:正.
【点评】此题属于辨识成正、反比例的量,就看这两种量是对应的比值一定,还是对应的乘积一定,再做出判断.
26.【答案】见试题解答内容
【分析】由m﹣n=0可知,m与n相等,则=1,即m和n这两个相关联的量的比值一定,根据两种相关联量成正比例的意义,m和n成正比例.
【解答】解:因为m﹣n=0
所以m=n
所以=1(一定)
根据=k(一定)x、y成正比例,m和n成正比例.
故答案为:√.
【点评】此题是考查正、反比例的判定.关键是看两种相关联的量所对应的数的比值(商)一定,还是积一定.
27.【答案】见试题解答内容
【分析】根据正反比例的意义,分析数量关系,找出一定的量,然后看那两个变量是比值一定还是乘积一定,从而判定成什么比例关系.
【解答】解:因为:长方形的周长=(长+宽)×2,
所以:长+宽=长方形的周长÷2(一定)(长方形的周长一定,它除以2也是一定的),
可以看出,当长方形的周长一定时,长和宽只是和一定,它们的比值和乘积都不是一定的,所以长方形的长和宽不成任何比例关系.
故答案为:×.
【点评】此题重点考查正比例和反比例的意义.
28.【答案】见试题解答内容
【分析】要想判定a和b成什么比例关系,必须根据式子,进行推导,再根据正反比例的意义,分析数量关系,找出一定的量,然后看那两个变量是比值一定还是乘积一定,从而判定成什么比例关系.
【解答】解:因为ab﹣8=17.5,
所以ab=17.5+8,
ab=25.5(一定);
可以看出,a和b是两个相关联的变化的量,它们相对应的乘积是25.5,是一定的,所以a和b成反比例关系.
故答案为:×.
【点评】此题重点考查正比例和反比例的意义.
29.【答案】见试题解答内容
【分析】根据长方体的表面积计算方法,分析数量关系,看看数量关系是不是符合正反比例的意义,从而判断.
【解答】解:长方体有6个面,对面相等,所以可以分成三组.长方体一个面的面积发生变化,虽然它的表面积也随着变化,但是其它的4个面没有发生变化,就会产生长方体的表面积与一个面的面积比值不一定和乘积也不一定的结果.所以长方体一个面的面积和它的表面积不成任何比例.
故答案为:×.
【点评】此题重点考查正比例和反比例的意义.
30.【答案】见试题解答内容
【分析】判断长方形长和宽成哪种比例,就看这两种量是否是对应的比值一定,还是积一定,如果是比值一定,就成正比例,如果积一定成反比例,据此作出判断.
【解答】解:因为长方形的面积(一定)=长×宽,
所以长方形的长和宽成反比例.
故答案为:×
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,还是对应的其它量一定,再做出判断.
四.应用题(共11小题)
31.【答案】见试题解答内容
【分析】(1)先计算路程与时间的比值,然后根据比值判断比例;
(2)依据正、反比例的意义,若两个量的商一定,则这两个量成正比例;若两个量的乘积一定,则这两个量成反比例,从而可以进行解答.
【解答】解:(1)8:2=4,10:2.5=4,20:5=4,40:10=4,60:15=4,因此,路程与时间的比值(速度)一定,路程和时间成正比例;
(2)因为路程÷时间=速度(一定),则当速度一定时,路程和时间成正比例;
因为路程÷速度=时间(一定),则当时间一定时,路程和速度成正比例;
因速度×时间=路程(一定),当路程一定时,速度和时间成反比例.
【点评】此题主要考查正、反比例的意义,即若a:b=k(一定),则a和b成正比例;若ab=k(一定),则a和b成反比例.
32.【答案】见试题解答内容
【分析】根据图表可知,铺2平方米用8块地板砖,铺6平方米用24块地板砖,8÷2=24÷6=4(一定),那么铺地面积与所需块数成正比例关系;设需要铺x块这样的地板砖,可得36:x=2:8,然后再根据比例的基本性质进行解答.
【解答】解:根据题意与分析可得:铺地面积与所需块数成正比例关系;
设需要铺x块这样的地板砖,根据题意,可得:
36:x=2:8
2x=36×8
2x÷2=36×8÷2
x=144
答:需要铺144块这样的地板砖.
【点评】本题关键是根据图表得出铺地面积与所需块数成正比例关系,然后再根据比例的意义和性质进行解答.
33.【答案】见试题解答内容
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.用字母表示=k(一定).
(1)根据平行四边形的面积公式:面积=底×高=3×底,填空即可.
(2)利用表中的数据计算出比值,比较大小即可.
(3)借助于平行四边形的面积公式理解其表示的意义即可.
(4)利用(2)的比值是否一定,来判定是否成正比例即可.
【解答】解:10×3=30;20×3=60.
底/cm 8 10 20 30
面积/cm2 24 30 60 90
(1)表中平行四边形的底和面积是相关联的量,平行四边形的面积随着底的变化而变化.
(2)=3;=3;=3;=3.比值大小相等,是个定值3.
(3)=高,比值表示的意义是平行四边形的高.
(4)相关联的两种量成正比例.
由(2)可知=3(一定),是比值一定,所以成正比例.
【点评】此题考查正比例关系的意义,理解成正比例的量的意义是解题的关键.
34.【答案】见试题解答内容
【分析】(1)根据题意知:表中有汽车数量和运货质量两种量,它们是两种相关联的量,一个量变大,另一个量也随着变大,它们的比值一定,所以汽车数量和运货质量成正比例关系.
(2)4:1=4,8:2=4,12:3=4,16:4=4,它们的比值相等.
(3)根据题意可知,这个比值表示每辆汽车的运货质量.
(4)相关联的两种量成正比例,因为它们的比值一定.
【解答】解:(1)表中有汽车数量和运货质量两种量,它们是两种相关联的量,一个量变大,另一个量也随着变大,它们的比值一定,所以汽车数量和运货质量成正比例关系.
(2)4:1=4,8:2=4,12:3=4,16:4=4,它们的比值相等.
(3)根据题意可知,这个比值表示每辆汽车的运货质量.
(4)相关联的两种量成正比例,因为它们的比值一定.
故答案为:汽车数量;运货质量;运货质量;汽车数量.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
35.【答案】见试题解答内容
【分析】(1)大米总量为40×10=400(kg),分别用每天的用量×所用的天数=大米总量的变形求出每天的用量或所用的天数,计算后填完整表格;
(2)从上表发现每天的用量与所用的天数成反比例关系;因为每天的用量与所用的天数的乘积是一个定值;
(3)因为400÷8=50(天).可以用50天;
(4)因为400÷100=4(kg).每天应该用4千克.
【解答】解:(1)
每天的用量/kg 50 40 25 20 5
所用的天数 8 10 16 20 80
(2)每天的用量与所用的天数成反比例关系;因为每天的用量与所用的天数的乘积是一个定值;
(3)400÷8=50(天);
答:可以用50天;
(4)400÷100=4(kg);
答:每天应该用4千克.
【点评】解答此题的关键是:弄清楚哪两种量成何比例,于是列比例即可求解.
36.【答案】见试题解答内容
【分析】(1)用煤的天数和用量是两个相关联的量,用总煤量除以用煤天数就是每天的用煤量,即用煤总量÷用煤天数=每天用煤量.如果每天的用煤量一定,煤的天数和用煤量成正比例.
(2)表示5天的纵与表示用煤量的直线的交点即表示5天的用煤量,即1.5吨;表示用煤量2.4吨的横轴与表示用煤量的直线的交点即表示用煤的天数,即2.4吨煤可以有8天.
【解答】解:(1)0.3÷1=0.3(吨)
0.6÷2=0.3(吨)
0.9÷3=0.3(吨)
……
每天的用煤量一定
即用煤总量÷用煤天数=每天用煤量(一定)
答:实验小学食堂用煤的天数和用煤量成正比例.
(2)答:食堂5天要用煤1.5吨,2.4吨煤可以用8天.
【点评】此题是考查辨析两种量成正、反比例.关键是看这两种相关联量中所对应的数的比值(商)一定还是积一定.
37.【答案】见试题解答内容
【分析】(1)此图象的特征:是一条经过原点的直线;从图象中很清晰的看出水箱内水的体积与注水的时间(或缩小)的变化规律,只要是两种相关联的量变化方向相同,就说明它们对应的比值一定,所以这两种量就成正比例关系;
(2)根据折线统计图可知,注水时间10分钟时,统计表中对应的水的体积为20升,即注水10分钟时水箱内的水的体积为20升,同理如果水要达到45升,需要注水22.5分钟.
【解答】解:(1)水箱内水的体积与注水的时间成正比例,因为水箱内水的体积与注水的时间的比值一定,且对应在一条直线上;
(2)45÷(10÷5)=22.5(分),
由图象可知10分能注水20升;注水45升需要22.5分.
【点评】此题考查借助直观的图象,辨识两种相关联的量成什么比例,只要图象是一条直线的,就成正比例;图象是一条曲线的,就成反比例;再根据成什么比例解决其它的问题.
38.【答案】见试题解答内容
【分析】①1小时行驶90千米,2小时行驶2个90千米,即180千米;3小时行3个90千米,即270千米;4小时行4个90千米,即360千米;5小时行5个90千米,即450千米;6小时行6个90千米,即540千米……然后填表,并在图中描出时间与路程对应的点,并这些点按顺序连起来.
②在这里速度一定,根据路程、速度、时间三者之间的关系,路程÷时间=速度(一定),再根据两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就是成正比例的量,由此即可判定时间和路程成正比例.
③根据表示时间、路程的拆线统计图即可估计2.5小时所行的路程、行675千米年需要的时间.
【解答】解:①先把上表补充完整,再根据表中的数据,在图中描出时间和路程的对应点,再把这些点按顺序连起来.
时间/时 1 2 3 4 5 6 …
路程/千米 90 180 270 360 450 540 …
②时间和路程成 正比例,理由是 路程÷时间=速度(一定).
③如图
用图象估计一下,2.5时行 225千米,行675千米需要 7.5小时.
故答案为:正,路程÷时间=速度(一定),225,7.5.
【点评】此主要是考查正、反比例的辨别,关键是看这两种相关联量中所对应的数的比值(商)一定还是积一定.
39.【答案】见试题解答内容
【分析】①找出这辆汽车的终点,根据图表找出对应的时间和路程.
②先根据“路程÷时间=速度”求出汽车的速度,进而根据“速度×时间=路程”进行解答即可.
③先根据“路程÷速度=时间”求出汽车行驶900km所需时间.
【解答】解:①这辆汽车的终点,根据图表找出对应的时间是3小时,路程是180千米.
答:这辆汽车行驶了3小时,行驶了180千米.
②180÷3=60(km/h),60×2.5=150(km).
答:这辆汽车2.5小时行驶了150千米.
③900÷60=15(h).
答:这辆汽车行驶900km要15小时
【点评】此题考查了学生从统计图中挖掘信息以及处理数据的能力,同时考查了正反比例的知识和对行程问题的掌握.
40.【答案】见试题解答内容
【分析】(1)此图象的特征:是一条经过原点的直线;从图象中很清晰的看出甲车行驶的路程与行驶时间同时扩大或缩小的变化规律,只要是两种相关联的量变化方向相同,就说明它们对应的比值一定,所以这两种量就成正比例关系;
(2)由图象可知:行驶150千米的路程甲车用的时间少,所以速度较快;据此解答即可.
【解答】解:(1)两辆车子所行的路程和时间成比例,因为是一条直线,所以成正比例;
(2)由图象可知:甲行驶150km,用4.2小时,乙行驶150km,用4.4小时,
4.2<4.4,
路程相同,用的时间越少,速度较快,即甲汽车的行驶速度快些;
【点评】此题主要考查对正比例的意义的运用:两种相关联的量,一种量变化,另一种量也随着变化,但两种量的比值一定,这两种量成正比例.
41.【答案】见试题解答内容
【分析】成正比例的量:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.用字母表示=k(一定).成正比例关系的图象是经过原点的一条直线.
(1)根据图中数据,算一算甲、乙中两种变量之间的比值是否一定即可.
(2)先求出1次甲比乙多运多少,再求出6次甲比乙多运多少即可.
【解答】解:(1)甲:====6(一定),是比值一定,所以甲车的运货量与运货次数成正比例关系.
乙:====4(一定),是比值一定,所以乙车的运货量与运货次数成正比例关系.
(2)18÷3﹣12÷3
=6﹣4
=2(吨)
2×6=12(吨)
答:甲、乙两车各运货6次,运货量相差12吨.
【点评】此题考查成正比例量,判定两个变化的量是不是成正比例关系,关键是看两个量的比值是否为定值.并且知道正比例关系的图象是经过原点的一条射线.
核心知识点
1.正比例和反比例的意义
【知识点归纳】
1.正比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.如果用字母x和y表示这两种相关联的量,用k表示它们的比值(一定),正比例关系可以用式子表示为:=k(一定).
2.反比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系.如果用字母x和y表示这两种相关联的量,用k表示它们的乘积(一定),反比例的关系可以表示为:xy=k(一定).
2.正比例
【知识点归纳】
正比例,简称正比,是指两种相关联的量,一种量变化,另一种量也随着变化。如果这两种量中相对应的两个数比值(或者说商)一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。
关联知识点
3.解比例
【知识点归纳】
根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项.求比例中的未知项,叫做解比例.
一般来说,求比例的未知项有以下两种情况:
(1)求未知外项=
(2)求未知内项=
一.选择题(共10小题)
1.如图表示两辆汽车所行驶的路程与相应时间关系的图象,下列关于图象描述错误的是( )
A.两辆汽车行驶的路程和时间都成正比例
B.从昆明到大理大约有350千米,甲车从昆明到大理大约要4个小时
C.从图象上看甲车的速度比乙车快
D.从图象上看乙车的速度比甲车快
2.学习下列哪个知识时不是运用了数形结合的方法?( )
A.小数乘法 B.正比例图像
C.折线统计图
3.下面各题中的两种量成正比例关系的有( )个.
①比例尺一定,两地的实际距离和图上距离;②如果y=5x,y和x;③圆的面积和直径;④订阅《小学生作文》的份数和总价;⑤书的总册数一定,每包的册数和包数;⑥大树的高度和大树影子的长度.
A.2 B.3 C.4 D.5
4.每平方米种植玉米的棵数一定,土地的面积和种植玉米的总棵数( )
A.成正比例 B.成反比例 C.不成比例
5.如果5a=3b,那么a和b( )关系.
A.成正比例 B.成反比例 C.不成比例
6.图中,( )表示的两个量成正比例关系。
A. B.
C. D.
7.如图中,表示正比例图象的是( )
A. B. C. D.
8.下面关系式,( )中x与y不成正比例(x、y均不为零).
A.x×=3 B.5x=6y C.4÷x=y D.x=y
9.下列图象表示正比例关系的是( )
A. B.
C. D.
10.圆柱的体积一定,底面积和高( )
A.成正比例 B.成反比例 C.不成比例
二.填空题(共10小题)
11.如表所示,当x和y成反比例时,空格里应填 ;当x和y成正比例时,空格里应填 。
x 6 2
y 12
12.如果x与y成正比例关系,下表中的“?”处应该是 ;如果x与y成反比例关系,右表中的“?”处应该是 。
x 180 ?
y 60 50
13.观察表格,如果x与y成正比例,那么m的值为 ;如果x与y成反比例,那么的值为 。
x 4 m
y 6 8
14.如下表,当x,y成正比例时,a的值是 ;当x、y成反比例时,a的值是 。
x 6 3
y 2 a
15.下表中x和y两个量成正比例,请把表格填写完整。
x 6 2.5
y 3 4 3.6
16.如图是李叔叔绘制的杨木的体积与质量变化规律图。从图中可以看出杨木的体积与质量成 比例关系。照这样计算,9m3杨木重 吨。
17.如果3a=4b(ab≠0),那么a:b= : ,a和b成 比例.
18.如果x和y成正比例,m= ,n= ;如果y和x成反比例,m= ,n= .
x 4 6 n
y 3 m 1.5
19.如果x与y成正比例,下表中的“?”应该是 ;如果x与y成反比例,下表中的“?”应该是 .
x 100 ?
y 80 40
20.观察如表:如果x和y成正比例,那么a等于 ;如果x和y成反比例,那么a等于 。
x 2 8
y 16 a
三.判断题(共10小题)
21.如果a÷2=b,且a、b≠0,那么a、b成正比例. .
22.在同一幅地图上,图上距离越大实际距离就越大. .
23.一根电线,用去的米数与剩下的米数成反比例. .
24.人的身高和体重成正比例. .
25.长方形的长一定,它的宽与面积成 比例.
26.m﹣n=0,m、n均不为0,m和n成正比例. .
27.长方形的周长一定时,长和宽成反比例. .
28.ab﹣8=17.25,则a和b不成比例 .
29.长方体一个面的面积和它的表面积成正比. .
30.长方形的面积一定,长和宽成正比例. .
四.应用题(共11小题)
31.在一次自行车越野赛中,小明骑车的时间与路程如下表.
时间(分) 8 10 20 40 60
路程(千米) 2 2.5 5 10 15
(1)路程和时间成什么比例?
(2)时间、路程和速度这三种量,在什么情况下成正比例,什么情况下成反比例?说明理由.
32.淘淘家在装修房屋时,买了同样大小的地板砖,铺地面积与所需块数的关系如图.他家的客厅面积是36m2,需要铺多少块这样的地板砖?(用比例解决问题)
33.平行四边形的高是3cm,先填表,再根据表中的数据回答问题.
底/cm 8 10 20 30
面积/cm2 24 90
(1)表中平行四边形的底和面积是 的量,平行四边形的 随着 的变化而变化.
(2)写出几组这两种量中相对应的两个数的比,求出比值,并比较比值的大小.
(3)上面求出的比值表示的意义是什么?
(4)表中相关联的两种量成正比例吗?为什么?
34.汽车数量与运货质量的数据如下表,根据表中的数据回答下面各题.
汽车数量/辆 1 2 3 4 5 6 7
运货质量/吨 4 8 12 16 20 24 28
(1)表中 和 是两种相关联的量, 随着 的变化而变化.
(2)写出几组这两种量中相对应的两个数的比,求出比值,并比较比值的大小.
(3)上面求出的比值表示的意义是什么?
(4)表中相关联的两种量成正比例吗?为什么?
35.食堂有一批大米.如表记录的是每天的用量和所用的天数.
每天的用量/kg 40 25 5
所用的天数 8 10 20 80
(1)把上表填写完整.
(2)每天的用量和所用的天数成反比例吗?为什么?
(3)如果每天用8kg,那么可以用多少天?
(4)如果计划用100天,那么每天应该用多少千克?
36.如图图象表示实验小学食堂的用煤天数和用煤量的关系.
(1)实验小学食堂用煤的天数和用煤量是否成正比例?
(2)根据图象判断,食堂5天要用煤多少吨?2.4吨煤可以用多少天?
37.下图表示一根水管不停地向水箱内注水时,水箱内水的体积的变化情况.
(1)水箱内水的体积与注水的时间成正比例吗?为什么?
(2)利用图象估一估,10分能注水多少升?注水45升需要多少分?再实际计算一下.
38.
时间/时 1 2 3 4 5 6 …
路程/千米 90 …
①先把上表补充完整,再根据表中的数据,在图中描出时间和路程的对应点,再把这些点按顺序连起来.
②时间和路程成 比例,理由是 .
③利用图象估计一下,2.5时行 千米,行675千米需要 小时.
39.如图中线段AB表示一辆汽车行驶的路程与时间的关系.
①这辆汽车行驶了多长时间?行驶了多少千米?
②这辆汽车2.5小时行驶了多少千米?
③这辆汽车行驶900km要多长时间?
40.根据甲、乙两车的行程图,回答下面的问题.
(1)甲、乙两车行驶的路程与时间是否成比例?说说理由.
(2)哪一辆汽车的行驶速度快些?
41.如图,甲、乙两车运货的吨数与次数的关系如图.
(1)甲车的运货量与运货次数成什么比例关系?乙车呢?
(2)甲、乙两车各运货6次,运货量相差多少吨?
第四单元第5课时正比例
参考答案与试题解析
一.选择题(共10小题)
1.【答案】D
【分析】根据图像都是直线可以判断两辆汽车行驶的路程和时间都成正比例,再根据两车行驶360千米所用的时间确定两车速度的快慢即可。
【解答】解:从图像中可以得到:
(1)两辆汽车形式的路程与时间的关系图像都是一条直线,所以两辆汽车行驶的路程和时间都成正比例。
(2)甲车4小时到达,乙车8小时到达,所以甲车的速度大于乙车的速度。
故选:D。
【点评】本题考查了正比例关系图像,要读懂图像反映出来的信息,并能根据信息解决问题。
2.【答案】A
【分析】小数乘法是一种计算,不需要图像;正比例图形和折线统计图都是图像(形)与数字的结合。
【解答】解:小数乘法是一种计算,不需要图像;正比例图形和折线统计图都是根据数据作图或根据图像(形)找数字信息或进行有关计算。
故选:A。
【点评】本题考查对小数乘法、正比例图像、折线统计图的理解。
3.【答案】B
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:①图上距离:实际距离=比例尺(一定),所以比例尺一定,图上距离和实际距离成正比例;
②y=5x,y:x=5(一定),所以x和y成正比例;
③圆的面积S=π(d÷2)2,=(一定),所以圆的面积与直径的平方成正比例,与直径不成比例;
④因为订阅《小学生作文》的总价÷份数=单价(一定),是订阅《小学生作文》的总价和份数的比值一定,
符合正比例的意义,所以订阅《小学生作文》的份数和总价成正比例;
⑤因为每包书的册数×包数=书的总册数(一定),所以每包数的册数和包数成反比例;
⑥同一时刻,同一地点物体的高度和影子的长度的比值一定,即物体的高度:影子的高度=比值(一定),所以同一时刻,同一地点物体的高度和影子的长度成正比例;本题没有说明同时同地,所以不成比例.
所以成正比例的有:①、②、④,3个.
故选:B.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
4.【答案】A
【分析】根据正反比例的意义,分析数量关系,找出一定的量,然后看那两个变量是比值一定还是乘积一定,从而判定成什么比例关系.
【解答】解:土地的面积和种植玉米的总棵数是两种相关联的量,它们与每平方米种植玉米的棵数有下面的关系:
种植玉米的总棵数:土地的面积=每平方米种植玉米的棵数(一定);
已知每平方米种植玉米的棵数一定,也就是土地的面积和种植玉米的总棵数的比值一定,所以土地的面积和种植玉米的总棵数成正比例.
故选:A.
【点评】此题重点考查正比例和反比例的意义.
5.【答案】A
【分析】先把等式变成a等于多少b,再根据正比例和反比例的意义求解.
【解答】解:5a=3b,
那么:a:b=;
是个定值,一个因数一定,积和另一个因数成正比例.
故选:A.
【点评】一个因数一定,积和另一个因数成正比例;积一定,两个因数成反比例.
6.【答案】D
【分析】要知道成正比例关系的图象特点是一条直线,相关联的两个量应是比值或商一定,反比例关系的图象是一条曲线,且一个量扩大、另一个量缩小;据此即可作出正确选择。
【解答】解:由图分析可知:
A.是一条曲折线,表示的两个量的乘积不一定,不成比例,不符合题意;
B.虽然是直线,但是表示的是一个量增加,而另一个量减少,不是比值或乘积一定,所以不成正比例,不符合题意;
C.是一条曲折线,表示的两个量的乘积不一定,不成比例,不符合题意;
D.是一条递增的直线,相对应的两个数据的比值一定,是正比例关系,符合题意。
故选:D。
【点评】本题是成正、反比例关系知识的拓展,是把数和形结合起来,研究两个相关联的量之间的关系。
7.【答案】B
【分析】根据正比例的意义是:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们之间的关系就是正比例关系,由此可知,正比例的图象是过原点的一条射线,据此解答。
【解答】解;根据正比例图象的特点可知,图B符合正比例图象的特点,所以图B是正比例图象。
故选:B。
【点评】此题考查的目的是理解掌握正比例的意义以及正比例图象的特点。
8.【答案】C
【分析】判断X与Y是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例.据此进行逐项分析再选择.
【解答】解:A、因为X×=3,则有=3(一定),是比值一定,所以X与Y成正比例;
B、因为5X=6Y,则有=(一定),是比值一定,所以X与Y成正比例;
C、因为4÷X=Y,则有XY=4(一定),是乘积一定,所以X与Y成反比例;
D、因为X=Y,则有=(一定),是比值一定,所以X与Y成正比例;
故选:C.
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量是否成正比例,就看这两种量是否是对应的比值一定,再做出判断.
9.【答案】C
【分析】成正比例关系的图象是经过原点的一条射线,据此回答即可.
【解答】解:选项A:不是过原点的一条射线,不成正比例关系,故错误;
选项B:不是过原点的一条射线,不成正比例关系,故错误;
选项C:是以原点为端点的一条射线,成正比例关系,故正确;
选项D:不是过原点的一条射线,不成正比例关系,故错误;
故选:C.
【点评】本题主要考查了成正比例关系的图象性质.
10.【答案】B
【分析】判定两种相关联的量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定就成反比例.
【解答】解:圆柱的底面积×高=体积(一定),是乘积一定,所以圆柱的底面积和高成反比例;
故选:B.
【点评】此题属于根据正、反比例的意义,判断两种相关联的量是成正比例还是成反比例,就看两种量是对应的比值一定,还是对应的乘积一定,再做出解答.
二.填空题(共10小题)
11.【答案】36;4。
【分析】两个相关联的量,若其比值一定,则两个量成正比例关系;若其乘积一定,则两个量成反比例关系。据此解答。
【解答】解:当x和y成反比例时,2y=6×12,解得y=36;
当x和y成正比例时,6:12=2:y,解得y=4。
故答案为:36;4。
【点评】本题考查利用比例的基本性质解比例。
12.【答案】150,216。
【分析】根据比例的基本性质,内项积等于外项积,据此把乘积式化为比例式;再根据两个相关联的量,若它们的比值一定,则它们成正比例;若它们的乘积一定,则它们成反比例。
【解答】解:x:50=180:60
x:50=3:1
x=50×3
x=150
50x=180×60
50x=10800
x=216
故答案为:150,216。
【点评】此题考查了解正比例和反比例的知识,要求学生掌握。
13.【答案】,3。
【分析】如果x与y成正比例,那么x与y的比值一定,如果x与y成反比例,那么x与y的乘积一定。
【解答】解:当x与y成正比例,
4:6=m:8
6m=32
m=
x与y成反比例,
8m=4×6
8m=24
m=3
故答案为:,3。
【点评】理解正比例和反比例的意义是解题关键。
14.【答案】1、4。
【分析】如果相关的两个量的比值一定,这两个量成正比例关系,如果相关的两个量的乘积一定,这两个量成反比例关系。
【解答】解:当x,y成正比例时,则=,解得a=1;
当x、y成反比例时,则6×2=3a,解得a=4。
所以当x,y成正比例时,a的值是1;当x、y成反比例时,a的值是4。
故答案为:1、4。
【点评】要熟知正比例和反比例的意义。
15.【答案】1.25,8,7.2,。
【分析】两个数成正比例,也就是x和y两个数的商不变,先求出这两个数的商,再根据被除数=除数×商,以及除数=被除数÷商即可解答。
【解答】解:6÷3=2
2.5÷2=1.25
4×2=8
3.6×2=7.2
÷2=
x 6 2.5 8 7.2
y 3 1.25 4 3.6
故答案为:1.25,8,7.2,。
【点评】此题主要考查学生对正比例的认识,以及利用正比例关系是解决问题的能力。
16.【答案】正、4.5。
【分析】比例图像是一条直线,所以杨木的体积与质量成正比例关系;根据图像可以看出,每m3杨木重0.5吨,据此求出9m3杨木的质量。
【解答】解:比例图像是一条直线,所以杨木的体积与质量成正比例关系。
9×0.5=4.5(吨)
答:9m3杨木重4.5吨。
故答案为:正、4.5。
【点评】本题考查了根据图像判断两种量成哪种比例关系及根据图像信息解决问题的能力。
17.【答案】见试题解答内容
【分析】根据比例的基本性质,两内项之积等于两外项之积,即可得解.
【解答】解:3a=4b,
a:b=4:3;
答:如果3a=4b,那么a:b=4:3,a和b成正比例.
故答案为:4,3,正.
【点评】两个相关联的量,它们的比值是固定值,则这两个量成正比例.
18.【答案】见试题解答内容
【分析】1.正比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.
2.反比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系.
然后根据比值一定,和乘积一定;列式解答即可.
【解答】解:如果x和y成正比例,m=6÷(4÷3)=4.5,
n=1.5×(4÷3)=2;
如果y和x成反比例,m=3×4÷6=2,
n=3×4÷1.5=8.
故答案为:4.5;2;2;8.
【点评】解答此题的关键是明白,两个数成正比例时,它们的商(比值)一定;成反比例时,它们的积一定.
19.【答案】见试题解答内容
【分析】(1)如果表中x和y成正比例,说明x和y对应的比值一定,根据两个比的比值相等列比例,并解比例即可;
(2)如果表中x和y成反比例,说明x和y对应的乘积一定,根据两个比的乘积相等列方程,并解方程即可.
【解答】解:
(1)100:80=x:40
80x=100×40
80x÷80=4000÷80
x=50
(2)40x=80×100
40x=8000
40x÷40=8000÷40,
x=200
故答案为:50,200.
【点评】此题主要考查了正比例和反比例的意义以及应用,要熟练掌握.
20.【答案】64,4。
【分析】成正比例就是两个量的比值一定,就是2:16=8:a,成反比例就是两个量的积一定,就是2×16=8a,计算即可解答。
【解答】解:2:16=8:a
2a=16×8
2a=128
a=64
2×16=8a
8a=32
a=4
答:如果x和y成正比例,那么a等于64,如果x和y成反比例,那么a等于 4。
故答案为:64,4。
【点评】本题考查的是正比例和反比例的意义,理解和运用正比例和反比例的意义是解答关键。
三.判断题(共10小题)
21.【答案】见试题解答内容
【分析】判断a与b是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例.
【解答】解:因为a÷2=b,且a、b≠0,
所以a÷b=2(一定),
即a与b的比值一定,
所以a、b成正比例,
故答案为:√.
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量是否成正比例,就看这两种量是否是对应的比值一定,再做出判断.
22.【答案】√
【分析】对的,因为比例尺相同,实际距离与图上距离成正比.
【解答】解:因为图上距离:实际距离=比例尺一定,
所以在同一幅地图上,图上距离与实际距离成正比例,
故在同一幅地图上,图上距离越大实际距离就越大.
故答案为:√.
【点评】本题结合比例尺考查了正比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.
23.【答案】见试题解答内容
【分析】①两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做成正比例关系.
②两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系.
③除了这两种情况,其余的都不成比例关系
【解答】解:用去的米数与剩下的米数相加是总米数,
它们与总量是加数、加数、和的关系,
它们的乘积不是一定的,比值也不是一定的.
所以用去的米数与剩下的米数不成任何比例关系.
故答案为:×.
【点评】此题重点考查辨识成正比例的量与成反比例的量.
24.【答案】×
【分析】判定两种相关联的量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定就成反比例;如果不是乘积或比值一定,就不成比例.
【解答】解:人的身高和体重虽是两种相关联的量,但是它们的乘积或比值都不一定,所以不成比例;
故答案为:×.
【点评】此题属于根据正、反比例的意义,判断两种相关联的量是成正比例还是成反比例,就看两种量是对应的比值一定,还是对应的乘积一定,再做出解答.
25.【答案】见试题解答内容
【分析】判断长方形的宽与面积成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例.
【解答】解:长方形的面积÷宽=长(一定),是比值一定,长方形的宽与面积成正比例.
故答案为:正.
【点评】此题属于辨识成正、反比例的量,就看这两种量是对应的比值一定,还是对应的乘积一定,再做出判断.
26.【答案】见试题解答内容
【分析】由m﹣n=0可知,m与n相等,则=1,即m和n这两个相关联的量的比值一定,根据两种相关联量成正比例的意义,m和n成正比例.
【解答】解:因为m﹣n=0
所以m=n
所以=1(一定)
根据=k(一定)x、y成正比例,m和n成正比例.
故答案为:√.
【点评】此题是考查正、反比例的判定.关键是看两种相关联的量所对应的数的比值(商)一定,还是积一定.
27.【答案】见试题解答内容
【分析】根据正反比例的意义,分析数量关系,找出一定的量,然后看那两个变量是比值一定还是乘积一定,从而判定成什么比例关系.
【解答】解:因为:长方形的周长=(长+宽)×2,
所以:长+宽=长方形的周长÷2(一定)(长方形的周长一定,它除以2也是一定的),
可以看出,当长方形的周长一定时,长和宽只是和一定,它们的比值和乘积都不是一定的,所以长方形的长和宽不成任何比例关系.
故答案为:×.
【点评】此题重点考查正比例和反比例的意义.
28.【答案】见试题解答内容
【分析】要想判定a和b成什么比例关系,必须根据式子,进行推导,再根据正反比例的意义,分析数量关系,找出一定的量,然后看那两个变量是比值一定还是乘积一定,从而判定成什么比例关系.
【解答】解:因为ab﹣8=17.5,
所以ab=17.5+8,
ab=25.5(一定);
可以看出,a和b是两个相关联的变化的量,它们相对应的乘积是25.5,是一定的,所以a和b成反比例关系.
故答案为:×.
【点评】此题重点考查正比例和反比例的意义.
29.【答案】见试题解答内容
【分析】根据长方体的表面积计算方法,分析数量关系,看看数量关系是不是符合正反比例的意义,从而判断.
【解答】解:长方体有6个面,对面相等,所以可以分成三组.长方体一个面的面积发生变化,虽然它的表面积也随着变化,但是其它的4个面没有发生变化,就会产生长方体的表面积与一个面的面积比值不一定和乘积也不一定的结果.所以长方体一个面的面积和它的表面积不成任何比例.
故答案为:×.
【点评】此题重点考查正比例和反比例的意义.
30.【答案】见试题解答内容
【分析】判断长方形长和宽成哪种比例,就看这两种量是否是对应的比值一定,还是积一定,如果是比值一定,就成正比例,如果积一定成反比例,据此作出判断.
【解答】解:因为长方形的面积(一定)=长×宽,
所以长方形的长和宽成反比例.
故答案为:×
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,还是对应的其它量一定,再做出判断.
四.应用题(共11小题)
31.【答案】见试题解答内容
【分析】(1)先计算路程与时间的比值,然后根据比值判断比例;
(2)依据正、反比例的意义,若两个量的商一定,则这两个量成正比例;若两个量的乘积一定,则这两个量成反比例,从而可以进行解答.
【解答】解:(1)8:2=4,10:2.5=4,20:5=4,40:10=4,60:15=4,因此,路程与时间的比值(速度)一定,路程和时间成正比例;
(2)因为路程÷时间=速度(一定),则当速度一定时,路程和时间成正比例;
因为路程÷速度=时间(一定),则当时间一定时,路程和速度成正比例;
因速度×时间=路程(一定),当路程一定时,速度和时间成反比例.
【点评】此题主要考查正、反比例的意义,即若a:b=k(一定),则a和b成正比例;若ab=k(一定),则a和b成反比例.
32.【答案】见试题解答内容
【分析】根据图表可知,铺2平方米用8块地板砖,铺6平方米用24块地板砖,8÷2=24÷6=4(一定),那么铺地面积与所需块数成正比例关系;设需要铺x块这样的地板砖,可得36:x=2:8,然后再根据比例的基本性质进行解答.
【解答】解:根据题意与分析可得:铺地面积与所需块数成正比例关系;
设需要铺x块这样的地板砖,根据题意,可得:
36:x=2:8
2x=36×8
2x÷2=36×8÷2
x=144
答:需要铺144块这样的地板砖.
【点评】本题关键是根据图表得出铺地面积与所需块数成正比例关系,然后再根据比例的意义和性质进行解答.
33.【答案】见试题解答内容
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.用字母表示=k(一定).
(1)根据平行四边形的面积公式:面积=底×高=3×底,填空即可.
(2)利用表中的数据计算出比值,比较大小即可.
(3)借助于平行四边形的面积公式理解其表示的意义即可.
(4)利用(2)的比值是否一定,来判定是否成正比例即可.
【解答】解:10×3=30;20×3=60.
底/cm 8 10 20 30
面积/cm2 24 30 60 90
(1)表中平行四边形的底和面积是相关联的量,平行四边形的面积随着底的变化而变化.
(2)=3;=3;=3;=3.比值大小相等,是个定值3.
(3)=高,比值表示的意义是平行四边形的高.
(4)相关联的两种量成正比例.
由(2)可知=3(一定),是比值一定,所以成正比例.
【点评】此题考查正比例关系的意义,理解成正比例的量的意义是解题的关键.
34.【答案】见试题解答内容
【分析】(1)根据题意知:表中有汽车数量和运货质量两种量,它们是两种相关联的量,一个量变大,另一个量也随着变大,它们的比值一定,所以汽车数量和运货质量成正比例关系.
(2)4:1=4,8:2=4,12:3=4,16:4=4,它们的比值相等.
(3)根据题意可知,这个比值表示每辆汽车的运货质量.
(4)相关联的两种量成正比例,因为它们的比值一定.
【解答】解:(1)表中有汽车数量和运货质量两种量,它们是两种相关联的量,一个量变大,另一个量也随着变大,它们的比值一定,所以汽车数量和运货质量成正比例关系.
(2)4:1=4,8:2=4,12:3=4,16:4=4,它们的比值相等.
(3)根据题意可知,这个比值表示每辆汽车的运货质量.
(4)相关联的两种量成正比例,因为它们的比值一定.
故答案为:汽车数量;运货质量;运货质量;汽车数量.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
35.【答案】见试题解答内容
【分析】(1)大米总量为40×10=400(kg),分别用每天的用量×所用的天数=大米总量的变形求出每天的用量或所用的天数,计算后填完整表格;
(2)从上表发现每天的用量与所用的天数成反比例关系;因为每天的用量与所用的天数的乘积是一个定值;
(3)因为400÷8=50(天).可以用50天;
(4)因为400÷100=4(kg).每天应该用4千克.
【解答】解:(1)
每天的用量/kg 50 40 25 20 5
所用的天数 8 10 16 20 80
(2)每天的用量与所用的天数成反比例关系;因为每天的用量与所用的天数的乘积是一个定值;
(3)400÷8=50(天);
答:可以用50天;
(4)400÷100=4(kg);
答:每天应该用4千克.
【点评】解答此题的关键是:弄清楚哪两种量成何比例,于是列比例即可求解.
36.【答案】见试题解答内容
【分析】(1)用煤的天数和用量是两个相关联的量,用总煤量除以用煤天数就是每天的用煤量,即用煤总量÷用煤天数=每天用煤量.如果每天的用煤量一定,煤的天数和用煤量成正比例.
(2)表示5天的纵与表示用煤量的直线的交点即表示5天的用煤量,即1.5吨;表示用煤量2.4吨的横轴与表示用煤量的直线的交点即表示用煤的天数,即2.4吨煤可以有8天.
【解答】解:(1)0.3÷1=0.3(吨)
0.6÷2=0.3(吨)
0.9÷3=0.3(吨)
……
每天的用煤量一定
即用煤总量÷用煤天数=每天用煤量(一定)
答:实验小学食堂用煤的天数和用煤量成正比例.
(2)答:食堂5天要用煤1.5吨,2.4吨煤可以用8天.
【点评】此题是考查辨析两种量成正、反比例.关键是看这两种相关联量中所对应的数的比值(商)一定还是积一定.
37.【答案】见试题解答内容
【分析】(1)此图象的特征:是一条经过原点的直线;从图象中很清晰的看出水箱内水的体积与注水的时间(或缩小)的变化规律,只要是两种相关联的量变化方向相同,就说明它们对应的比值一定,所以这两种量就成正比例关系;
(2)根据折线统计图可知,注水时间10分钟时,统计表中对应的水的体积为20升,即注水10分钟时水箱内的水的体积为20升,同理如果水要达到45升,需要注水22.5分钟.
【解答】解:(1)水箱内水的体积与注水的时间成正比例,因为水箱内水的体积与注水的时间的比值一定,且对应在一条直线上;
(2)45÷(10÷5)=22.5(分),
由图象可知10分能注水20升;注水45升需要22.5分.
【点评】此题考查借助直观的图象,辨识两种相关联的量成什么比例,只要图象是一条直线的,就成正比例;图象是一条曲线的,就成反比例;再根据成什么比例解决其它的问题.
38.【答案】见试题解答内容
【分析】①1小时行驶90千米,2小时行驶2个90千米,即180千米;3小时行3个90千米,即270千米;4小时行4个90千米,即360千米;5小时行5个90千米,即450千米;6小时行6个90千米,即540千米……然后填表,并在图中描出时间与路程对应的点,并这些点按顺序连起来.
②在这里速度一定,根据路程、速度、时间三者之间的关系,路程÷时间=速度(一定),再根据两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就是成正比例的量,由此即可判定时间和路程成正比例.
③根据表示时间、路程的拆线统计图即可估计2.5小时所行的路程、行675千米年需要的时间.
【解答】解:①先把上表补充完整,再根据表中的数据,在图中描出时间和路程的对应点,再把这些点按顺序连起来.
时间/时 1 2 3 4 5 6 …
路程/千米 90 180 270 360 450 540 …
②时间和路程成 正比例,理由是 路程÷时间=速度(一定).
③如图
用图象估计一下,2.5时行 225千米,行675千米需要 7.5小时.
故答案为:正,路程÷时间=速度(一定),225,7.5.
【点评】此主要是考查正、反比例的辨别,关键是看这两种相关联量中所对应的数的比值(商)一定还是积一定.
39.【答案】见试题解答内容
【分析】①找出这辆汽车的终点,根据图表找出对应的时间和路程.
②先根据“路程÷时间=速度”求出汽车的速度,进而根据“速度×时间=路程”进行解答即可.
③先根据“路程÷速度=时间”求出汽车行驶900km所需时间.
【解答】解:①这辆汽车的终点,根据图表找出对应的时间是3小时,路程是180千米.
答:这辆汽车行驶了3小时,行驶了180千米.
②180÷3=60(km/h),60×2.5=150(km).
答:这辆汽车2.5小时行驶了150千米.
③900÷60=15(h).
答:这辆汽车行驶900km要15小时
【点评】此题考查了学生从统计图中挖掘信息以及处理数据的能力,同时考查了正反比例的知识和对行程问题的掌握.
40.【答案】见试题解答内容
【分析】(1)此图象的特征:是一条经过原点的直线;从图象中很清晰的看出甲车行驶的路程与行驶时间同时扩大或缩小的变化规律,只要是两种相关联的量变化方向相同,就说明它们对应的比值一定,所以这两种量就成正比例关系;
(2)由图象可知:行驶150千米的路程甲车用的时间少,所以速度较快;据此解答即可.
【解答】解:(1)两辆车子所行的路程和时间成比例,因为是一条直线,所以成正比例;
(2)由图象可知:甲行驶150km,用4.2小时,乙行驶150km,用4.4小时,
4.2<4.4,
路程相同,用的时间越少,速度较快,即甲汽车的行驶速度快些;
【点评】此题主要考查对正比例的意义的运用:两种相关联的量,一种量变化,另一种量也随着变化,但两种量的比值一定,这两种量成正比例.
41.【答案】见试题解答内容
【分析】成正比例的量:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.用字母表示=k(一定).成正比例关系的图象是经过原点的一条直线.
(1)根据图中数据,算一算甲、乙中两种变量之间的比值是否一定即可.
(2)先求出1次甲比乙多运多少,再求出6次甲比乙多运多少即可.
【解答】解:(1)甲:====6(一定),是比值一定,所以甲车的运货量与运货次数成正比例关系.
乙:====4(一定),是比值一定,所以乙车的运货量与运货次数成正比例关系.
(2)18÷3﹣12÷3
=6﹣4
=2(吨)
2×6=12(吨)
答:甲、乙两车各运货6次,运货量相差12吨.
【点评】此题考查成正比例量,判定两个变化的量是不是成正比例关系,关键是看两个量的比值是否为定值.并且知道正比例关系的图象是经过原点的一条射线.
