2023-2024学年寒假查漏补缺检测卷-高中数学北师大版必修第二册(含答案)
文档属性
| 名称 | 2023-2024学年寒假查漏补缺检测卷-高中数学北师大版必修第二册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 436.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-30 10:54:39 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2023-2024学年寒假查漏补缺检测卷-高中数学北师大版必修第二册
一、选择题
1. 若复数为纯虚数,则实数m的值为( )
A.1 B.-1 C.2 D.-2
2.已知复数满足,,则( )
A.1 B.2 C. D.
3.设,,,则的大小关系正确的是( )
A. B. C. D.
4.已知角 的终边经过点 , 则 的值为 ( )
A. B. C.1 D.
5.已知,则( )
A. B. C. D.
6.光岳楼位于山东聊城古城中央,主体结构建于明洪武七年(13年),它是迄今为止全国现存古代建筑中最古老、最雄伟的木构楼阁之一,享有“虽黄鹤、岳阳亦当望拜”之誉,光岳楼的墩台为砖石砌成的正四棱台,如图所示,该墩台上底面边长约为32m,下底面边长约为34.5m,高约为9m,则该墩台的斜高约为( )(参考数据:)
A.9.1m B.10.9m C.11.2m D.12.1m
7.已知正四棱锥的底面边长是,体积是,那么这个四棱锥的侧棱长为( )
A. B.2 C. D.
8.若两异面直线 与 的方向向量分别是 , ,则直线 与 的夹角为( )
A.30° B.60° C.120° D.150°
二、多项选择题
9. 已知下列各角: (1) : (2) ; (3) ; (4) , 其中是第二象限角的是( )
A.(1) B.(2) C.(3) D.(4)
10.下列结论正确的是( )
A.是第三象限角
B.若圆心角为的扇形的弧长为,则该扇形的面积为
C.若角的终边上有一点,则
D.若角为锐角,则角为钝角
11.函数的部分图像如图所示,则下列说法中错误的是( )
A.的最小正周期是
B.是奇函数.
C.在上单调递增
D.直线是曲线的一条对称轴
12.将函数的图象向左平移个单位长度,再把所得图象上各点的横坐标变为原来的倍,纵坐标不变,得到的图象,下面四个结论中,错误的是( )
A.函数在区间上为增函数
B.将函数的图象向左平移个单位长度后得到的图象关于轴对称
C.点是函数图象的一个对称中心
D.函数在上的最大值为1
三、填空题
13.已知,则的值为 .
14.已知平面向量,,若与共线,则 .
15.将函数的图象向右平移个并位长度可以得到函数的图象,若函数在区间内有零点,无最值,则的取值范围是 .
16. 在三棱锥中,平面,则三棱锥的内切球的表面积等于 .
四、解答题
17.已知i是虚数单位,.
(1)求;
(2)若复数的虚部为-1,且是纯虚数,求.
18.已知,且为第二象限角.
(1)求的值;
(2)求的值.
19.已知
(1)化简;
(2)若,求的值.
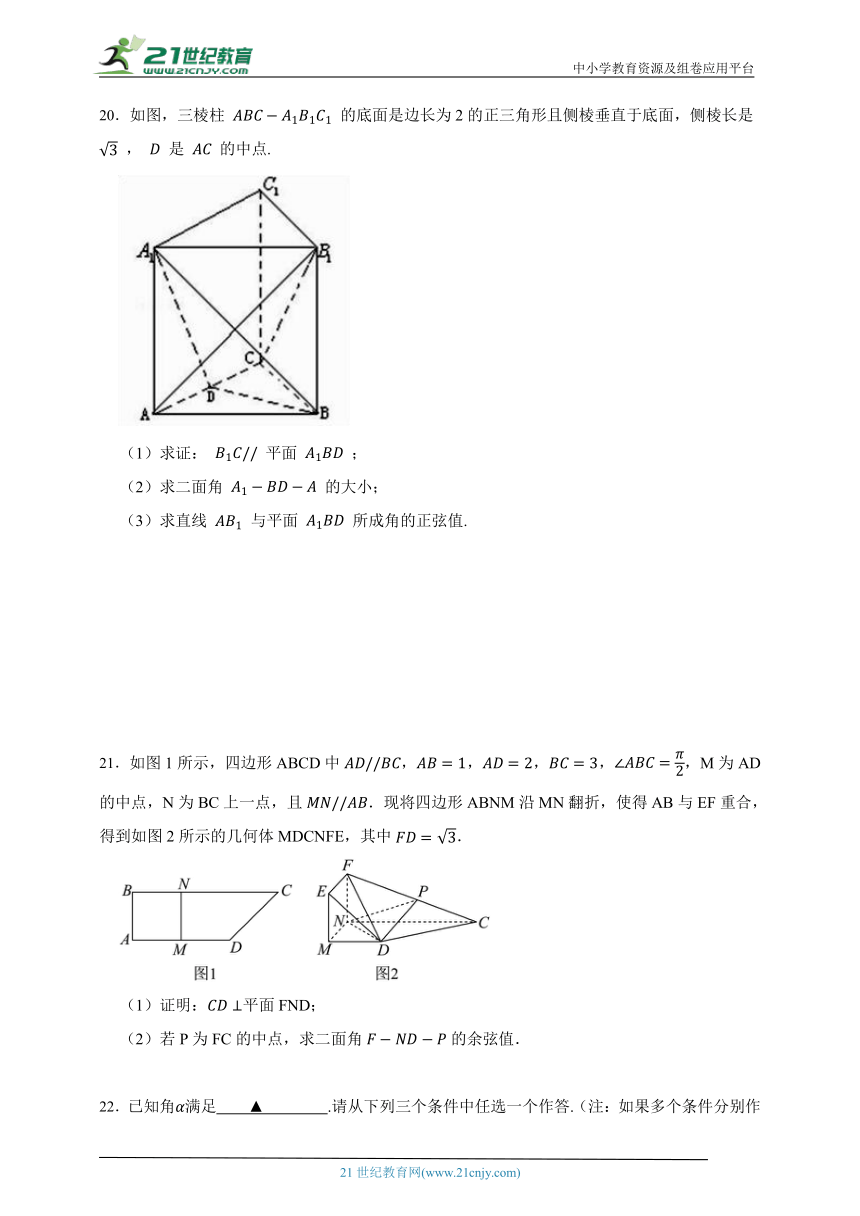
20.如图,三棱柱 的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是 , 是 的中点.
(1)求证: 平面 ;
(2)求二面角 的大小;
(3)求直线 与平面 所成角的正弦值.
21.如图1所示,四边形ABCD中,,,,,M为AD的中点,N为BC上一点,且.现将四边形ABNM沿MN翻折,使得AB与EF重合,得到如图2所示的几何体MDCNFE,其中.
(1)证明:平面FND;
(2)若P为FC的中点,求二面角的余弦值.
22.已知角满足 ▲ .请从下列三个条件中任选一个作答.(注:如果多个条件分别作答,按第一个解答计分).
条件①:角的终边与单位圆的交点为.
条件②:角满足;
条件③:角满足.
(1)求的值;
(2)求的值.
答案解析部分
1.【答案】D
2.【答案】C
3.【答案】A
4.【答案】D
5.【答案】A
6.【答案】A
7.【答案】C
8.【答案】B
9.【答案】C,D
10.【答案】B,C
11.【答案】B,C
12.【答案】A,B,C
13.【答案】3
14.【答案】
15.【答案】
16.【答案】
17.【答案】(1)解:根据复数的运算法则,
可得,
所以.
(2)解:设,则,
因为是纯虚数,所以且,
解得,所以.
18.【答案】(1)解:因为,且为第二象限角,(没说明第二象限角求值的扣1分)
所以;
(2)解:
19.【答案】(1)解:
(2)解:由(1)易得,
所以
20.【答案】(1)解:设 与 相交于点 ,连接 ,则 为 中点,
为 中点, .
又 平面 , 平面
平面 .
(2)解: 正三棱柱 , 底面 .
又 , ,
就是二面角 的平面角.
, , .
,即二面角 的大小是
(3)解:由(2)作 , 为垂足.
,平面 平面 ,平面 平面 ,
平面 ,
平面 , .
, 平面 ,连接 ,则 就是直线 与平面 所成的角.
, , 在 中, ,
, .
.
直线 与平面 所成的角的正弦值为 .
(备注:也可以建立空间直角坐标系来解答.)
21.【答案】(1)证明:∵四边形ABCD中,,,,,
M为AD的中点,且,
∴四边形ABNM为正方形,且边长为1,
∴题图2中,四边形EMNF是边长为1的正方形,故,
又,,∴,∴,
又,,平面MDCN,平面MDCN,
∴平面MDCN,∵平面MDCN,∴,
易知,∴,∴,
又,平面,平面,
∴平面;
(2)解:解法一:由(1)知平面MDCN,又,
以N为坐标原点,建立空间直角坐标系,如图所示,
则,,,,
∴,,,
设平面FND的法向量为,则,
令,令,则,∴,
设平面PND的法向量为,则,
令,则,,∴,
∴,
∴二面角的正弦值为.
22.【答案】(1)解:条件①:因为角的终边与单位圆的交点为,所以,
又因为,可得,所以,可得
条件②,因为角满足,
又因为,即可得,所以,可得.
条件③:因为角满足,又因为,
即,可得
又,所以,即.
(2)解:,
由(1)可知:,当时,原式;
当时,原式
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年寒假查漏补缺检测卷-高中数学北师大版必修第二册
一、选择题
1. 若复数为纯虚数,则实数m的值为( )
A.1 B.-1 C.2 D.-2
2.已知复数满足,,则( )
A.1 B.2 C. D.
3.设,,,则的大小关系正确的是( )
A. B. C. D.
4.已知角 的终边经过点 , 则 的值为 ( )
A. B. C.1 D.
5.已知,则( )
A. B. C. D.
6.光岳楼位于山东聊城古城中央,主体结构建于明洪武七年(13年),它是迄今为止全国现存古代建筑中最古老、最雄伟的木构楼阁之一,享有“虽黄鹤、岳阳亦当望拜”之誉,光岳楼的墩台为砖石砌成的正四棱台,如图所示,该墩台上底面边长约为32m,下底面边长约为34.5m,高约为9m,则该墩台的斜高约为( )(参考数据:)
A.9.1m B.10.9m C.11.2m D.12.1m
7.已知正四棱锥的底面边长是,体积是,那么这个四棱锥的侧棱长为( )
A. B.2 C. D.
8.若两异面直线 与 的方向向量分别是 , ,则直线 与 的夹角为( )
A.30° B.60° C.120° D.150°
二、多项选择题
9. 已知下列各角: (1) : (2) ; (3) ; (4) , 其中是第二象限角的是( )
A.(1) B.(2) C.(3) D.(4)
10.下列结论正确的是( )
A.是第三象限角
B.若圆心角为的扇形的弧长为,则该扇形的面积为
C.若角的终边上有一点,则
D.若角为锐角,则角为钝角
11.函数的部分图像如图所示,则下列说法中错误的是( )
A.的最小正周期是
B.是奇函数.
C.在上单调递增
D.直线是曲线的一条对称轴
12.将函数的图象向左平移个单位长度,再把所得图象上各点的横坐标变为原来的倍,纵坐标不变,得到的图象,下面四个结论中,错误的是( )
A.函数在区间上为增函数
B.将函数的图象向左平移个单位长度后得到的图象关于轴对称
C.点是函数图象的一个对称中心
D.函数在上的最大值为1
三、填空题
13.已知,则的值为 .
14.已知平面向量,,若与共线,则 .
15.将函数的图象向右平移个并位长度可以得到函数的图象,若函数在区间内有零点,无最值,则的取值范围是 .
16. 在三棱锥中,平面,则三棱锥的内切球的表面积等于 .
四、解答题
17.已知i是虚数单位,.
(1)求;
(2)若复数的虚部为-1,且是纯虚数,求.
18.已知,且为第二象限角.
(1)求的值;
(2)求的值.
19.已知
(1)化简;
(2)若,求的值.
20.如图,三棱柱 的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是 , 是 的中点.
(1)求证: 平面 ;
(2)求二面角 的大小;
(3)求直线 与平面 所成角的正弦值.
21.如图1所示,四边形ABCD中,,,,,M为AD的中点,N为BC上一点,且.现将四边形ABNM沿MN翻折,使得AB与EF重合,得到如图2所示的几何体MDCNFE,其中.
(1)证明:平面FND;
(2)若P为FC的中点,求二面角的余弦值.
22.已知角满足 ▲ .请从下列三个条件中任选一个作答.(注:如果多个条件分别作答,按第一个解答计分).
条件①:角的终边与单位圆的交点为.
条件②:角满足;
条件③:角满足.
(1)求的值;
(2)求的值.
答案解析部分
1.【答案】D
2.【答案】C
3.【答案】A
4.【答案】D
5.【答案】A
6.【答案】A
7.【答案】C
8.【答案】B
9.【答案】C,D
10.【答案】B,C
11.【答案】B,C
12.【答案】A,B,C
13.【答案】3
14.【答案】
15.【答案】
16.【答案】
17.【答案】(1)解:根据复数的运算法则,
可得,
所以.
(2)解:设,则,
因为是纯虚数,所以且,
解得,所以.
18.【答案】(1)解:因为,且为第二象限角,(没说明第二象限角求值的扣1分)
所以;
(2)解:
19.【答案】(1)解:
(2)解:由(1)易得,
所以
20.【答案】(1)解:设 与 相交于点 ,连接 ,则 为 中点,
为 中点, .
又 平面 , 平面
平面 .
(2)解: 正三棱柱 , 底面 .
又 , ,
就是二面角 的平面角.
, , .
,即二面角 的大小是
(3)解:由(2)作 , 为垂足.
,平面 平面 ,平面 平面 ,
平面 ,
平面 , .
, 平面 ,连接 ,则 就是直线 与平面 所成的角.
, , 在 中, ,
, .
.
直线 与平面 所成的角的正弦值为 .
(备注:也可以建立空间直角坐标系来解答.)
21.【答案】(1)证明:∵四边形ABCD中,,,,,
M为AD的中点,且,
∴四边形ABNM为正方形,且边长为1,
∴题图2中,四边形EMNF是边长为1的正方形,故,
又,,∴,∴,
又,,平面MDCN,平面MDCN,
∴平面MDCN,∵平面MDCN,∴,
易知,∴,∴,
又,平面,平面,
∴平面;
(2)解:解法一:由(1)知平面MDCN,又,
以N为坐标原点,建立空间直角坐标系,如图所示,
则,,,,
∴,,,
设平面FND的法向量为,则,
令,令,则,∴,
设平面PND的法向量为,则,
令,则,,∴,
∴,
∴二面角的正弦值为.
22.【答案】(1)解:条件①:因为角的终边与单位圆的交点为,所以,
又因为,可得,所以,可得
条件②,因为角满足,
又因为,即可得,所以,可得.
条件③:因为角满足,又因为,
即,可得
又,所以,即.
(2)解:,
由(1)可知:,当时,原式;
当时,原式
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
