人教版数学八年级下册同步练习18.1.1 平行四边形的边、角性质(含答案)
文档属性
| 名称 | 人教版数学八年级下册同步练习18.1.1 平行四边形的边、角性质(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 348.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-29 10:54:35 | ||
图片预览


文档简介
第十八章 平行四边形
18.1 平行四边形
第1课时 平行四边形的边、角性质
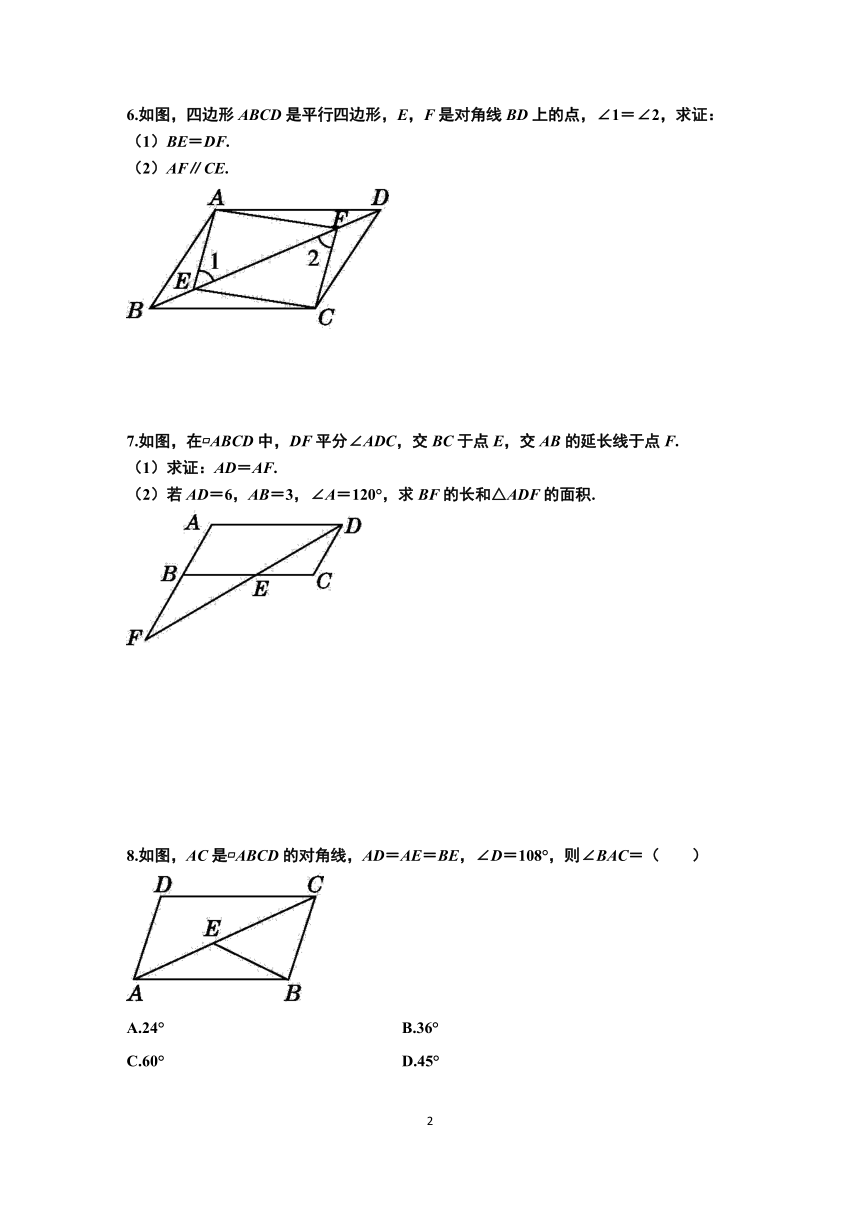
1.如图, ABCD的周长为30,AD∶AB=3∶2,那么BC的长度是( )
A.9 B.12 C.15 D.18
2.在 ABCD中,若∠A=2∠B,则∠A的度数为( )
A.60° B.90°
C.120° D.150°
3.锐角为45°的两个平行四边形的位置如图所示,若∠1=α,则∠2=( )
A.α-45° B.90°-α
C.135°-α D.180°-2α
4.如图,在 ABCD中,∠A=70°,DC=DB,则∠CDB= .
5.如图,△ABC的顶点B在 ODEF的边DE上,若BC恰好平分∠ABE,已知∠2=110°,则∠1= .
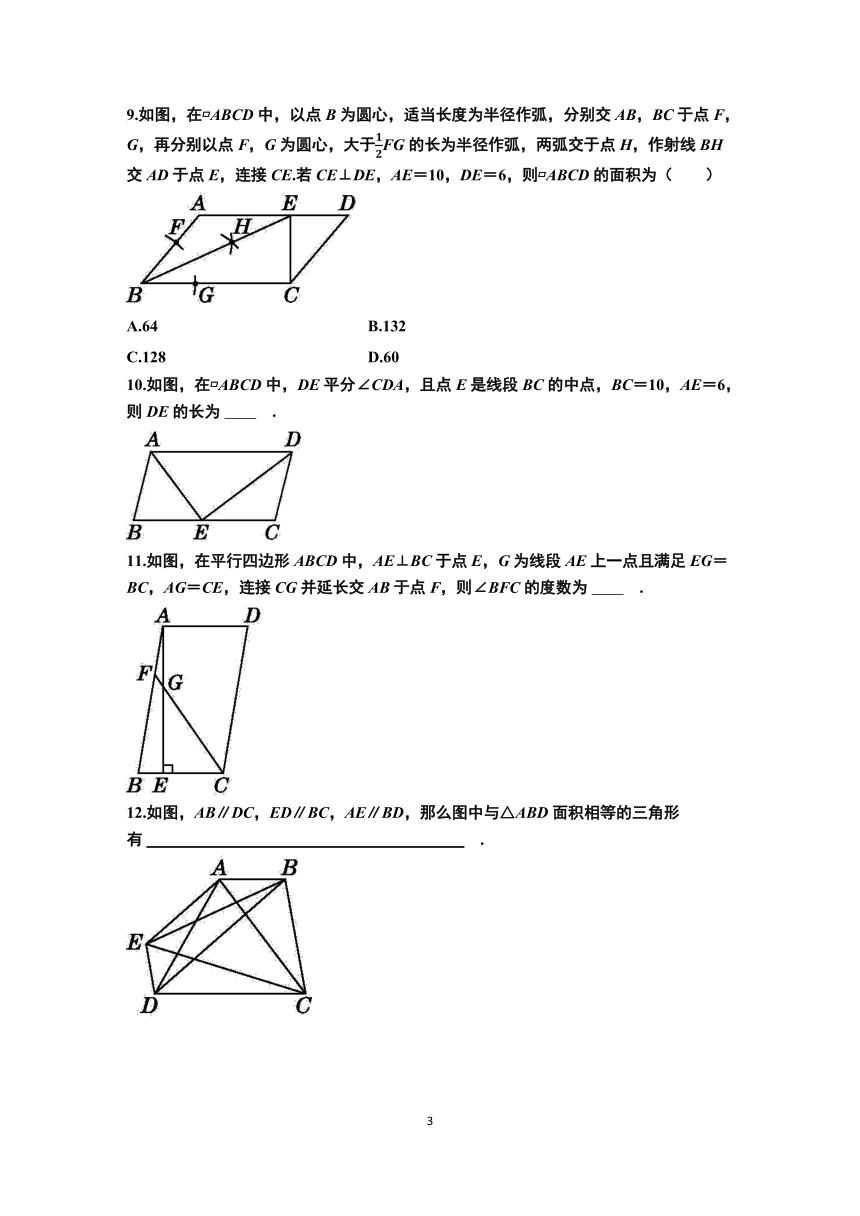
6.如图,四边形ABCD是平行四边形,E,F是对角线BD上的点,∠1=∠2,求证:
(1)BE=DF.
(2)AF∥CE.
7.如图,在 ABCD中,DF平分∠ADC,交BC于点E,交AB的延长线于点F.
(1)求证:AD=AF.
(2)若AD=6,AB=3,∠A=120°,求BF的长和△ADF的面积.
8.如图,AC是 ABCD的对角线,AD=AE=BE,∠D=108°,则∠BAC=( )
A.24° B.36°
C.60° D.45°
9.如图,在 ABCD中,以点B为圆心,适当长度为半径作弧,分别交AB,BC于点F,G,再分别以点F,G为圆心,大于FG的长为半径作弧,两弧交于点H,作射线BH交AD于点E,连接CE.若CE⊥DE,AE=10,DE=6,则 ABCD的面积为( )
A.64 B.132
C.128 D.60
10.如图,在 ABCD中,DE平分∠CDA,且点E是线段BC的中点,BC=10,AE=6,则DE的长为 .
11.如图,在平行四边形ABCD中,AE⊥BC于点E,G为线段AE上一点且满足EG=BC,AG=CE,连接CG并延长交AB于点F,则∠BFC的度数为 .
12.如图,AB∥DC,ED∥BC,AE∥BD,那么图中与△ABD面积相等的三角形有 .
13.如图,在 ABCD中,点E是BC边的中点,连接AE并延长与DC的延长线交于点F.
(1)求证:CF=CD.
(2)若AD=2AB,连接DE,试判断DE与AF的位置关系,并说明理由.
14.(1)在图①,图②,图③中,已知 ABCD的顶点A,B,D的坐标,写图①,图②,图③中的顶点C的坐标,它们分别是 , , .
(2)在图④中,给出 ABCD的顶点A,B,D的坐标(如图所示),求出顶点C的坐标(点C的坐标用含a,b,c,d,e,f的代数式表示).
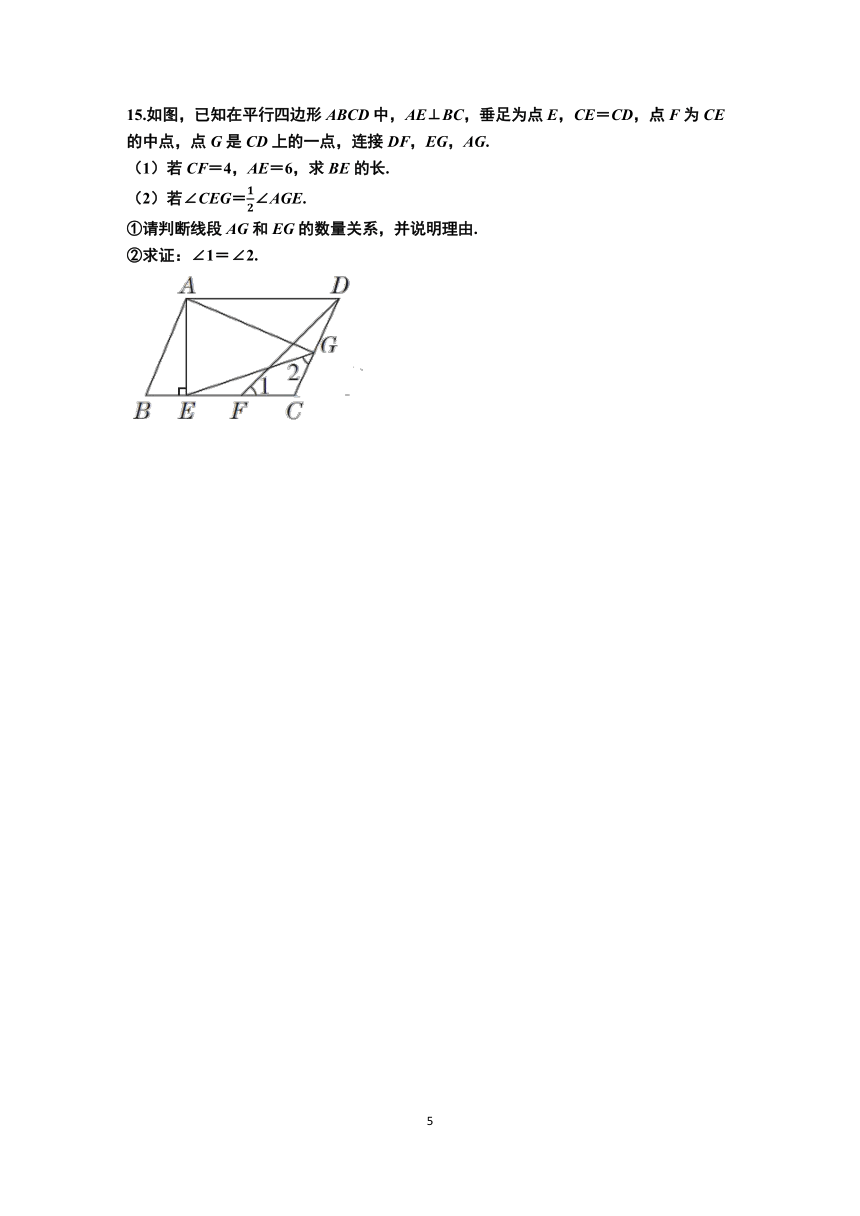
15.如图,已知在平行四边形ABCD中,AE⊥BC,垂足为点E,CE=CD,点F为CE的中点,点G是CD上的一点,连接DF,EG,AG.
(1)若CF=4,AE=6,求BE的长.
(2)若∠CEG=∠AGE.
①请判断线段AG和EG的数量关系,并说明理由.
②求证:∠1=∠2.
16.问题提出:
(1)如图,△ABC为等边三角形,边长为6 cm,动点M从点B出发,沿着三角形的三条边顺时针方向以2 cm/s的速度运动,动点N从点C出发,沿着三角形的三条边逆时针方向以1 cm/s的速度运动.动点M,N同时出发,当点M在AB上运动且MN⊥AB时,求点M运动的时间.
问题解决:
(2)某小区有一个边长为4 m的等边三角形花坛,六一将至,物业借助花坛△ABC举办了一个有奖活动,一家四口举着一根长绳在花坛三边任选位置站立(不能站在各边中点上),四人拉紧、拉直长绳后(长绳可有剩余)可得到一个四边形,如工作人员量得这个四边形是平行四边形,则可领取奖品一份.笑笑和爸爸、妈妈、奶奶一起参加活动,四人的方案是奶奶在A点站立不动,妈妈在△ABC边上某点D处站立不动,爸爸从点B出发,沿着花坛顺时针方向以2 m/s的速度走动(可看作花坛边上运动的点M),同时笑笑从点C出发,沿着花坛逆时针方向以1 m/s的速度走动(可看作花坛边上运动的点N).若笑笑出发不到2 s,一家人就得奖了,那么妈妈所选的位置D距点C多少米?
11
参考答案
1.A 2.C 3.A 4.40° 5.35°
6.证明:(1)∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD,∴∠ABE=∠CDF.
∵∠1=∠2,∴∠AEB=∠CFD.
在△ABE和△CDF中,
∴△ABE≌△CDF(AAS),
∴BE=DF.
(2)由(1)可知△ABE≌△CDF,∴AE=CF.
又∵∠1=∠2,EF=EF,
∴△AEF≌△CFE,∴∠AFE=∠CEF,∴AF∥CE.
7.(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,
∴∠CDE=∠F.
∵DF平分∠ADC,∴∠ADE=∠CDE.
∴∠F=∠ADF,∴AD=AF.
(2)解:∵AD=AF=6,AB=3,∴BF=AF-AB=3.
如图,过点D作DH⊥FA,交FA的延长线于H,则∠H=90°.
∵∠BAD=120°,∴∠DAH=60°,∴∠ADH=30°,
∴AH=AD=3,∴DH==3,
∴△ADF的面积=AF·DH=×6×3=9.
8.A
9.C 点拨:∵AE=10,DE=6,∴AD=16.由题意得BE平分∠ABC,∴∠ABE=∠CBE.∵四边形ABCD为平行四边形,∴AD∥BC,AB=CD,∴∠CBE=∠AEB,∴∠ABE=∠AEB,∴AB=AE=10,∴CD=10.∵CE⊥DE,∴∠CED=90°.∵DE=6,CD=10,∴CE===8,∴ ABCD的面积为AD×CE=16×8=128.故选C.
10.8 点拨:∵四边形ABCD是平行四边形,∴AD=BC,AB=CD,AD∥BC,AB∥CD.
∴∠EDA=∠DEC.∵DE平分∠CDA,∴∠EDC=∠EDA,∴∠EDC=∠DEC.∴EC=CD.
∵点E是线段BC的中点,BC=10,∴EC=BE=5,∴AB=CD=EC=5,∴AB=BE,∴∠BAE=∠AEB.∵AD∥BC,∴∠DAE=∠AEB,∴∠BAE=∠DAE.∵AB∥CD,
∴∠BAD+∠ADC=180°,∴∠DAE+∠ADE=90°,
∴∠AED=90°.∴△AED是直角三角形.∵AE=6,AD=BC=10,∴DE===8.
11.45° 点拨:连接DG,在平行四边形ABCD中,AB∥CD,AD∥BC,AD=BC,∵AE⊥BC,∴∠GEC=90°,AE⊥AD,∴∠DAG=90°.∵EG=BC,AD=BC,∴EG=AD.
在△ADG和△EGC中,,
∴△ADG≌△EGC(SAS),
∴DG=CG,∠ADG=∠EGC.∵∠ADG+∠AGD=90°,
∴∠EGC+∠AGD=90°,
∴∠DGC=90°,∴△DGC是等腰直角三角形,
∴∠DCG=45°.∵AB∥CD,
∴∠BFC=∠DCG=45°.
12.△BDE,△EDC,△ABC
13.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵点F为DC的延长线上的一点,
∴AB∥DF,
∴∠BAE=∠CFE,∠ECF=∠EBA.
∵E为BC的中点,∴BE=CE.
在△BAE和△CFE中,,
∴△BAE≌△CFE(AAS),∴AB=CF.
∵AB=CD,
∴CF=CD.
(2)解:DE⊥AF,理由如下:
由(1)得,CF=CD,△BAE≌△CFE,
∴AE=EF,DF=2CD.
∵AB=CD,∴DF=2AB.
∵AD=2AB,∴AD=DF.又∵AE=EF,
∴DE⊥AF.
14.解:(1)(5,2);(e+c,d);(c+e-a,d)
(2)如图,分别过点A,B,C,D作x轴的垂线,垂足分别为A1,B1,C1,D1,
过A作AE⊥BB1于点E,过D作DF⊥CC1于点F,则∠AEB=∠DFC=90°.
∵四边形ABCD是平行四边形,
∴CD=BA,CD∥BA,
∴∠ABC+∠BCF+∠FCD=180°.
易知BB1∥CC1,
∴∠EBA+∠ABC+∠BCF=180°.
∴∠EBA=∠FCD.
在△BEA和△CFD中,
∴△BEA≌△CFD(AAS).
∴DF=AE=a-c,CF=BE=d-b.
设C(x,y).则DF=e-x,CF=y-f.
∴e-x=a-c,y-f=d-b,
∴x=e+c-a,y=f+d-b.
∴C(e+c-a,f+d-b).
15.(1)解:∵CE=CD,点F为CE的中点,CF=4,
∴CD=CE=2CF=8.
∵四边形ABCD是平行四边形,∴AB=CD=8.
∵AE⊥BC,∴∠AEB=90°.
在Rt△ABE中,由勾股定理,得BE===2.
(2)①解:AG=EG,理由如下:
延长BC交AG的延长线于H,如图所示.
∵∠CEG=∠AGE,∠AGE=∠CEG+∠CHG,
∴∠CEG=∠CHG.
∵AE⊥BC,∴∠AEC=90°,
∴∠AEG+∠CEG=90°,∠EAG+∠CHG=90°,
∴∠AEG=∠EAG,
∴AG=EG.
②证明:由①,得∠CEG=∠CHG,AG=EG,
∴AG=EG=HG.
∵四边形ABCD是平行四边形,∴AD∥BH,
∴∠DAG=∠CHG,∠ADG=∠HCG.
在△ADG和△HCG中,
∴△ADG≌△HCG(AAS),∴DG=CG,
∴CG=CD=CE.
∵点F为CE的中点,
∴CF=CE,∴CF=CG.
在△CDF和△CEG中, ,
∴△CDF≌△CEG(SAS),∴∠1=∠2.
16.解:(1)设点M运动的时间为t s(0≤t≤3),则BM=2t cm,CN=t cm,∴AM=(6-2t)cm,AN=(6-t)cm.
∵MN⊥AB,∴∠AMN=90°.
∵△ABC为等边三角形,
∴∠A=60°,∴∠ANM=30°,∴AM=AN.
∴6-2t=(6-t),解得t=2,
∴点M运动的时间为2s.
(2)点M,D,N的位置如图所示.
∵△ABC是边长为4 m的等边三角形,
∴AB=BC=AC=4 m,∠A=∠B=∠C=60°.
设笑笑出发x s,一家人就得奖了,
则笑笑走了x m,笑笑的爸爸走了2x m,
∴CN=x m,BM=2x m,
∴AM=(4-2x)m.
∵四边形ANDM为平行四边形,
∴DN=AM=(4-2x)m,DN∥AB,
∴∠NDC=∠B=60°,∠DNC=∠A=60°,
∴∠DNC=∠C=∠NDC=60°,
∴△CDN是等边三角形,
∴DN=CD=CN=x m,
∴x=4-2x,
解得x=,∴CD=m.
∴妈妈所选的位置D距点C m.
18.1 平行四边形
第1课时 平行四边形的边、角性质
1.如图, ABCD的周长为30,AD∶AB=3∶2,那么BC的长度是( )
A.9 B.12 C.15 D.18
2.在 ABCD中,若∠A=2∠B,则∠A的度数为( )
A.60° B.90°
C.120° D.150°
3.锐角为45°的两个平行四边形的位置如图所示,若∠1=α,则∠2=( )
A.α-45° B.90°-α
C.135°-α D.180°-2α
4.如图,在 ABCD中,∠A=70°,DC=DB,则∠CDB= .
5.如图,△ABC的顶点B在 ODEF的边DE上,若BC恰好平分∠ABE,已知∠2=110°,则∠1= .
6.如图,四边形ABCD是平行四边形,E,F是对角线BD上的点,∠1=∠2,求证:
(1)BE=DF.
(2)AF∥CE.
7.如图,在 ABCD中,DF平分∠ADC,交BC于点E,交AB的延长线于点F.
(1)求证:AD=AF.
(2)若AD=6,AB=3,∠A=120°,求BF的长和△ADF的面积.
8.如图,AC是 ABCD的对角线,AD=AE=BE,∠D=108°,则∠BAC=( )
A.24° B.36°
C.60° D.45°
9.如图,在 ABCD中,以点B为圆心,适当长度为半径作弧,分别交AB,BC于点F,G,再分别以点F,G为圆心,大于FG的长为半径作弧,两弧交于点H,作射线BH交AD于点E,连接CE.若CE⊥DE,AE=10,DE=6,则 ABCD的面积为( )
A.64 B.132
C.128 D.60
10.如图,在 ABCD中,DE平分∠CDA,且点E是线段BC的中点,BC=10,AE=6,则DE的长为 .
11.如图,在平行四边形ABCD中,AE⊥BC于点E,G为线段AE上一点且满足EG=BC,AG=CE,连接CG并延长交AB于点F,则∠BFC的度数为 .
12.如图,AB∥DC,ED∥BC,AE∥BD,那么图中与△ABD面积相等的三角形有 .
13.如图,在 ABCD中,点E是BC边的中点,连接AE并延长与DC的延长线交于点F.
(1)求证:CF=CD.
(2)若AD=2AB,连接DE,试判断DE与AF的位置关系,并说明理由.
14.(1)在图①,图②,图③中,已知 ABCD的顶点A,B,D的坐标,写图①,图②,图③中的顶点C的坐标,它们分别是 , , .
(2)在图④中,给出 ABCD的顶点A,B,D的坐标(如图所示),求出顶点C的坐标(点C的坐标用含a,b,c,d,e,f的代数式表示).
15.如图,已知在平行四边形ABCD中,AE⊥BC,垂足为点E,CE=CD,点F为CE的中点,点G是CD上的一点,连接DF,EG,AG.
(1)若CF=4,AE=6,求BE的长.
(2)若∠CEG=∠AGE.
①请判断线段AG和EG的数量关系,并说明理由.
②求证:∠1=∠2.
16.问题提出:
(1)如图,△ABC为等边三角形,边长为6 cm,动点M从点B出发,沿着三角形的三条边顺时针方向以2 cm/s的速度运动,动点N从点C出发,沿着三角形的三条边逆时针方向以1 cm/s的速度运动.动点M,N同时出发,当点M在AB上运动且MN⊥AB时,求点M运动的时间.
问题解决:
(2)某小区有一个边长为4 m的等边三角形花坛,六一将至,物业借助花坛△ABC举办了一个有奖活动,一家四口举着一根长绳在花坛三边任选位置站立(不能站在各边中点上),四人拉紧、拉直长绳后(长绳可有剩余)可得到一个四边形,如工作人员量得这个四边形是平行四边形,则可领取奖品一份.笑笑和爸爸、妈妈、奶奶一起参加活动,四人的方案是奶奶在A点站立不动,妈妈在△ABC边上某点D处站立不动,爸爸从点B出发,沿着花坛顺时针方向以2 m/s的速度走动(可看作花坛边上运动的点M),同时笑笑从点C出发,沿着花坛逆时针方向以1 m/s的速度走动(可看作花坛边上运动的点N).若笑笑出发不到2 s,一家人就得奖了,那么妈妈所选的位置D距点C多少米?
11
参考答案
1.A 2.C 3.A 4.40° 5.35°
6.证明:(1)∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD,∴∠ABE=∠CDF.
∵∠1=∠2,∴∠AEB=∠CFD.
在△ABE和△CDF中,
∴△ABE≌△CDF(AAS),
∴BE=DF.
(2)由(1)可知△ABE≌△CDF,∴AE=CF.
又∵∠1=∠2,EF=EF,
∴△AEF≌△CFE,∴∠AFE=∠CEF,∴AF∥CE.
7.(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,
∴∠CDE=∠F.
∵DF平分∠ADC,∴∠ADE=∠CDE.
∴∠F=∠ADF,∴AD=AF.
(2)解:∵AD=AF=6,AB=3,∴BF=AF-AB=3.
如图,过点D作DH⊥FA,交FA的延长线于H,则∠H=90°.
∵∠BAD=120°,∴∠DAH=60°,∴∠ADH=30°,
∴AH=AD=3,∴DH==3,
∴△ADF的面积=AF·DH=×6×3=9.
8.A
9.C 点拨:∵AE=10,DE=6,∴AD=16.由题意得BE平分∠ABC,∴∠ABE=∠CBE.∵四边形ABCD为平行四边形,∴AD∥BC,AB=CD,∴∠CBE=∠AEB,∴∠ABE=∠AEB,∴AB=AE=10,∴CD=10.∵CE⊥DE,∴∠CED=90°.∵DE=6,CD=10,∴CE===8,∴ ABCD的面积为AD×CE=16×8=128.故选C.
10.8 点拨:∵四边形ABCD是平行四边形,∴AD=BC,AB=CD,AD∥BC,AB∥CD.
∴∠EDA=∠DEC.∵DE平分∠CDA,∴∠EDC=∠EDA,∴∠EDC=∠DEC.∴EC=CD.
∵点E是线段BC的中点,BC=10,∴EC=BE=5,∴AB=CD=EC=5,∴AB=BE,∴∠BAE=∠AEB.∵AD∥BC,∴∠DAE=∠AEB,∴∠BAE=∠DAE.∵AB∥CD,
∴∠BAD+∠ADC=180°,∴∠DAE+∠ADE=90°,
∴∠AED=90°.∴△AED是直角三角形.∵AE=6,AD=BC=10,∴DE===8.
11.45° 点拨:连接DG,在平行四边形ABCD中,AB∥CD,AD∥BC,AD=BC,∵AE⊥BC,∴∠GEC=90°,AE⊥AD,∴∠DAG=90°.∵EG=BC,AD=BC,∴EG=AD.
在△ADG和△EGC中,,
∴△ADG≌△EGC(SAS),
∴DG=CG,∠ADG=∠EGC.∵∠ADG+∠AGD=90°,
∴∠EGC+∠AGD=90°,
∴∠DGC=90°,∴△DGC是等腰直角三角形,
∴∠DCG=45°.∵AB∥CD,
∴∠BFC=∠DCG=45°.
12.△BDE,△EDC,△ABC
13.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵点F为DC的延长线上的一点,
∴AB∥DF,
∴∠BAE=∠CFE,∠ECF=∠EBA.
∵E为BC的中点,∴BE=CE.
在△BAE和△CFE中,,
∴△BAE≌△CFE(AAS),∴AB=CF.
∵AB=CD,
∴CF=CD.
(2)解:DE⊥AF,理由如下:
由(1)得,CF=CD,△BAE≌△CFE,
∴AE=EF,DF=2CD.
∵AB=CD,∴DF=2AB.
∵AD=2AB,∴AD=DF.又∵AE=EF,
∴DE⊥AF.
14.解:(1)(5,2);(e+c,d);(c+e-a,d)
(2)如图,分别过点A,B,C,D作x轴的垂线,垂足分别为A1,B1,C1,D1,
过A作AE⊥BB1于点E,过D作DF⊥CC1于点F,则∠AEB=∠DFC=90°.
∵四边形ABCD是平行四边形,
∴CD=BA,CD∥BA,
∴∠ABC+∠BCF+∠FCD=180°.
易知BB1∥CC1,
∴∠EBA+∠ABC+∠BCF=180°.
∴∠EBA=∠FCD.
在△BEA和△CFD中,
∴△BEA≌△CFD(AAS).
∴DF=AE=a-c,CF=BE=d-b.
设C(x,y).则DF=e-x,CF=y-f.
∴e-x=a-c,y-f=d-b,
∴x=e+c-a,y=f+d-b.
∴C(e+c-a,f+d-b).
15.(1)解:∵CE=CD,点F为CE的中点,CF=4,
∴CD=CE=2CF=8.
∵四边形ABCD是平行四边形,∴AB=CD=8.
∵AE⊥BC,∴∠AEB=90°.
在Rt△ABE中,由勾股定理,得BE===2.
(2)①解:AG=EG,理由如下:
延长BC交AG的延长线于H,如图所示.
∵∠CEG=∠AGE,∠AGE=∠CEG+∠CHG,
∴∠CEG=∠CHG.
∵AE⊥BC,∴∠AEC=90°,
∴∠AEG+∠CEG=90°,∠EAG+∠CHG=90°,
∴∠AEG=∠EAG,
∴AG=EG.
②证明:由①,得∠CEG=∠CHG,AG=EG,
∴AG=EG=HG.
∵四边形ABCD是平行四边形,∴AD∥BH,
∴∠DAG=∠CHG,∠ADG=∠HCG.
在△ADG和△HCG中,
∴△ADG≌△HCG(AAS),∴DG=CG,
∴CG=CD=CE.
∵点F为CE的中点,
∴CF=CE,∴CF=CG.
在△CDF和△CEG中, ,
∴△CDF≌△CEG(SAS),∴∠1=∠2.
16.解:(1)设点M运动的时间为t s(0≤t≤3),则BM=2t cm,CN=t cm,∴AM=(6-2t)cm,AN=(6-t)cm.
∵MN⊥AB,∴∠AMN=90°.
∵△ABC为等边三角形,
∴∠A=60°,∴∠ANM=30°,∴AM=AN.
∴6-2t=(6-t),解得t=2,
∴点M运动的时间为2s.
(2)点M,D,N的位置如图所示.
∵△ABC是边长为4 m的等边三角形,
∴AB=BC=AC=4 m,∠A=∠B=∠C=60°.
设笑笑出发x s,一家人就得奖了,
则笑笑走了x m,笑笑的爸爸走了2x m,
∴CN=x m,BM=2x m,
∴AM=(4-2x)m.
∵四边形ANDM为平行四边形,
∴DN=AM=(4-2x)m,DN∥AB,
∴∠NDC=∠B=60°,∠DNC=∠A=60°,
∴∠DNC=∠C=∠NDC=60°,
∴△CDN是等边三角形,
∴DN=CD=CN=x m,
∴x=4-2x,
解得x=,∴CD=m.
∴妈妈所选的位置D距点C m.
