人教版数学八年级下册同步练习18.1.4 三角形的中位线(含答案)
文档属性
| 名称 | 人教版数学八年级下册同步练习18.1.4 三角形的中位线(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 252.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-29 00:00:00 | ||
图片预览

文档简介
第4课时 三角形的中位线
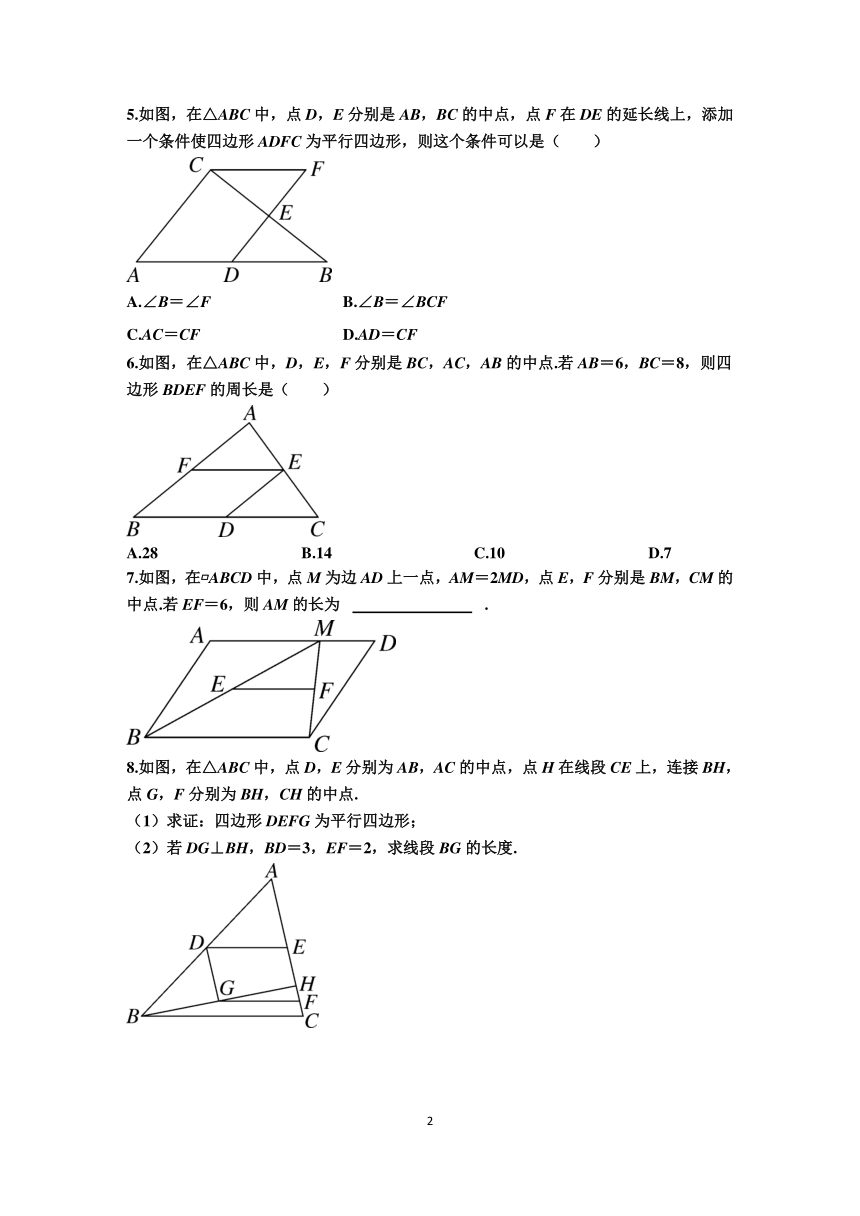
1.如图,A,B两点被池塘隔开,A,B,C三点不共线.设AC,BC的中点分别为M,N.若MN=3m,则AB=( )
A.4m B.6m
C.8m D.10m
2.如图,在△ABC中,点D,E分别是AB,BC的中点.若∠C=44°,则∠DEB=( )
A.22° B.44°
C.46° D.136°
3.如图,在△ABC中,D,E,F分别是AB,AC,BC的中点,若AB=10,AC=8,BC=12,则△DEF的周长为 .
4.如图,△ABC的中线BE,CD相交于点O,F,G分别是BO,CO的中点,求证:DF=EG.
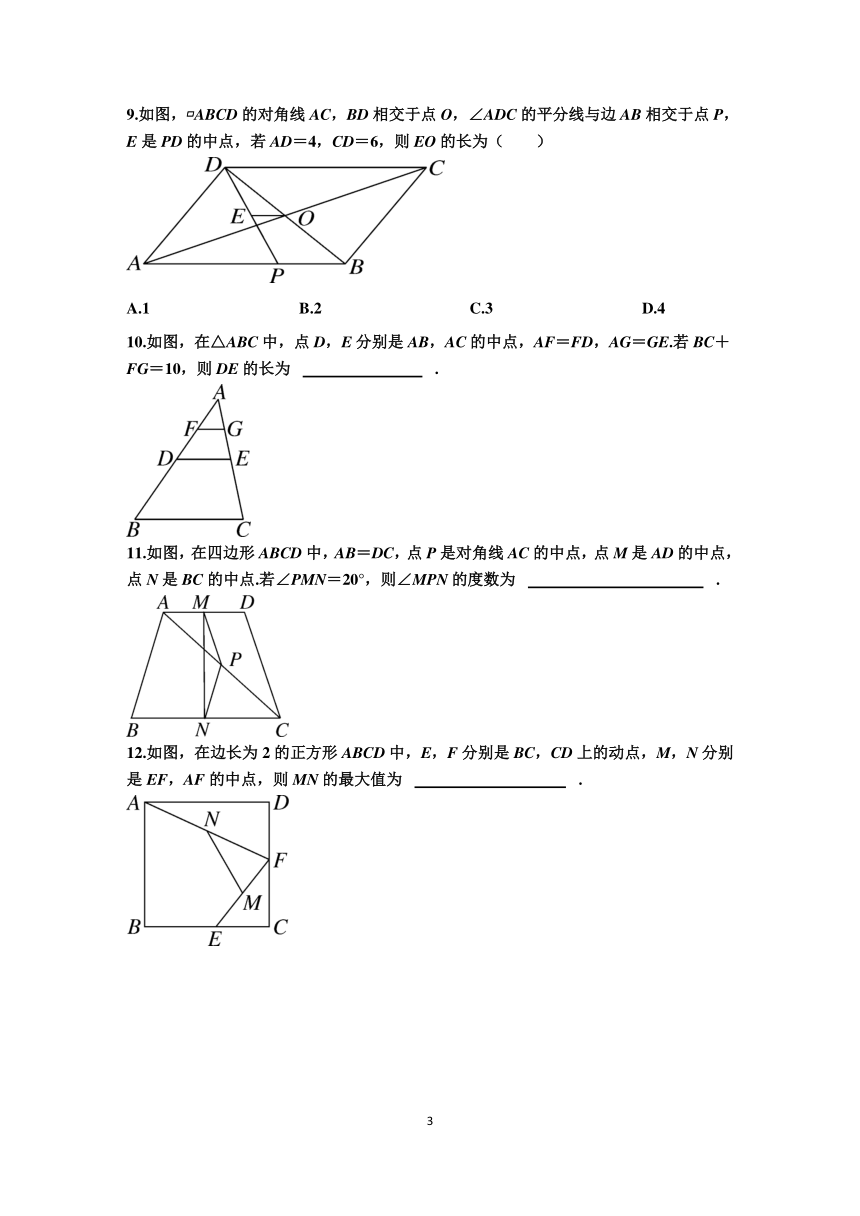
5.如图,在△ABC中,点D,E分别是AB,BC的中点,点F在DE的延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件可以是( )
A.∠B=∠F B.∠B=∠BCF
C.AC=CF D.AD=CF
6.如图,在△ABC中,D,E,F分别是BC,AC,AB的中点.若AB=6,BC=8,则四边形BDEF的周长是( )
A.28 B.14 C.10 D.7
7.如图,在 ABCD中,点M为边AD上一点,AM=2MD,点E,F分别是BM,CM的中点.若EF=6,则AM的长为 .
8.如图,在△ABC中,点D,E分别为AB,AC的中点,点H在线段CE上,连接BH,点G,F分别为BH,CH的中点.
(1)求证:四边形DEFG为平行四边形;
(2)若DG⊥BH,BD=3,EF=2,求线段BG的长度.
9.如图, ABCD的对角线AC,BD相交于点O,∠ADC的平分线与边AB相交于点P,E是PD的中点,若AD=4,CD=6,则EO的长为( )
A.1 B.2 C.3 D.4
10.如图,在△ABC中,点D,E分别是AB,AC的中点,AF=FD,AG=GE.若BC+FG=10,则DE的长为 .
11.如图,在四边形ABCD中,AB=DC,点P是对角线AC的中点,点M是AD的中点,点N是BC的中点.若∠PMN=20°,则∠MPN的度数为 .
12.如图,在边长为2的正方形ABCD中,E,F分别是BC,CD上的动点,M,N分别是EF,AF的中点,则MN的最大值为 .
13.如图,在Rt△ABC中,∠BAC=90°,点E,F分别是BC,AC的中点,延长BA到点D,使得AB=2AD,连接DE,DF,AE,EF,AF与DE相交于点O.
(1)求证:AF与DE互相平分;
(2)如果AB=6,BC=10,求DO的长.
14.如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.
(1)如图①,BE的延长线与AC边相交于点D,求证:EF=(AC-AB);
(2)如图②,请写出线段AB,AC,EF之间的数量关系,并说明理由.
1
参考答案
1. B
2. B
3. 15
4. 证明:∵点D是AB的中点,点F是BO的中点,
∴DF=AO.
同理可得EG=AO,∴DF=EG.
5. B
6. B
7. 8
8. (1)证明:∵点D,E分别为AB,AC的中点,点G,F
分别为BH,CH的中点,
∴DE是△ABC的中位线,GF是△HBC的中位线.
∴DE∥BC,DE=BC,GF∥BC,GF=BC.
∴DE∥GF,DE=GF.
∴四边形DEFG为平行四边形.
(2)因为四边形DEFG为平行四边形
9. A
10. 4
11. 140°
12.
13. (1)证明:∵点E,F分别是BC,AC的中点,
∴EF∥AB,AB=2EF.
∵AB=2AD,点D是BA延长线上的一点,
∴AD=EF,AD∥EF.
∴四边形ADFE是平行四边形.
∴AF与DE互相平分.
(2)解:在Rt△ABC中,
∵∠BAC=90°,AB=6,BC=10,
∴AC==8.
∵EF∥AD,∴∠EFO=180°-∠BAC=90°.
∵EF=AB=3,OA=OF=AC=2,
∴在Rt△OEF中,OE==.
∴DO=OE=.
14.(1)证明:∵AE⊥BD,AE平分∠BAC,
∴易得△ABE≌△ADE(ASA).
∴AB=AD,BE=DE.
∵点F是BC的中点,
∴EF=DC=(AC-AD)=(AC-AB).
(2)解:EF=(AB-AC).理由如下:
如图②,延长AC交BE的延长线于点P.
∵AE⊥BP,AE平分∠BAC,
∴易得△ABE≌△APE(ASA).
∴AB=AP,BE=PE.
∵点F是BC的中点,
∴EF=PC=(AP-AC)=(AB-AC).
1.如图,A,B两点被池塘隔开,A,B,C三点不共线.设AC,BC的中点分别为M,N.若MN=3m,则AB=( )
A.4m B.6m
C.8m D.10m
2.如图,在△ABC中,点D,E分别是AB,BC的中点.若∠C=44°,则∠DEB=( )
A.22° B.44°
C.46° D.136°
3.如图,在△ABC中,D,E,F分别是AB,AC,BC的中点,若AB=10,AC=8,BC=12,则△DEF的周长为 .
4.如图,△ABC的中线BE,CD相交于点O,F,G分别是BO,CO的中点,求证:DF=EG.
5.如图,在△ABC中,点D,E分别是AB,BC的中点,点F在DE的延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件可以是( )
A.∠B=∠F B.∠B=∠BCF
C.AC=CF D.AD=CF
6.如图,在△ABC中,D,E,F分别是BC,AC,AB的中点.若AB=6,BC=8,则四边形BDEF的周长是( )
A.28 B.14 C.10 D.7
7.如图,在 ABCD中,点M为边AD上一点,AM=2MD,点E,F分别是BM,CM的中点.若EF=6,则AM的长为 .
8.如图,在△ABC中,点D,E分别为AB,AC的中点,点H在线段CE上,连接BH,点G,F分别为BH,CH的中点.
(1)求证:四边形DEFG为平行四边形;
(2)若DG⊥BH,BD=3,EF=2,求线段BG的长度.
9.如图, ABCD的对角线AC,BD相交于点O,∠ADC的平分线与边AB相交于点P,E是PD的中点,若AD=4,CD=6,则EO的长为( )
A.1 B.2 C.3 D.4
10.如图,在△ABC中,点D,E分别是AB,AC的中点,AF=FD,AG=GE.若BC+FG=10,则DE的长为 .
11.如图,在四边形ABCD中,AB=DC,点P是对角线AC的中点,点M是AD的中点,点N是BC的中点.若∠PMN=20°,则∠MPN的度数为 .
12.如图,在边长为2的正方形ABCD中,E,F分别是BC,CD上的动点,M,N分别是EF,AF的中点,则MN的最大值为 .
13.如图,在Rt△ABC中,∠BAC=90°,点E,F分别是BC,AC的中点,延长BA到点D,使得AB=2AD,连接DE,DF,AE,EF,AF与DE相交于点O.
(1)求证:AF与DE互相平分;
(2)如果AB=6,BC=10,求DO的长.
14.如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.
(1)如图①,BE的延长线与AC边相交于点D,求证:EF=(AC-AB);
(2)如图②,请写出线段AB,AC,EF之间的数量关系,并说明理由.
1
参考答案
1. B
2. B
3. 15
4. 证明:∵点D是AB的中点,点F是BO的中点,
∴DF=AO.
同理可得EG=AO,∴DF=EG.
5. B
6. B
7. 8
8. (1)证明:∵点D,E分别为AB,AC的中点,点G,F
分别为BH,CH的中点,
∴DE是△ABC的中位线,GF是△HBC的中位线.
∴DE∥BC,DE=BC,GF∥BC,GF=BC.
∴DE∥GF,DE=GF.
∴四边形DEFG为平行四边形.
(2)因为四边形DEFG为平行四边形
9. A
10. 4
11. 140°
12.
13. (1)证明:∵点E,F分别是BC,AC的中点,
∴EF∥AB,AB=2EF.
∵AB=2AD,点D是BA延长线上的一点,
∴AD=EF,AD∥EF.
∴四边形ADFE是平行四边形.
∴AF与DE互相平分.
(2)解:在Rt△ABC中,
∵∠BAC=90°,AB=6,BC=10,
∴AC==8.
∵EF∥AD,∴∠EFO=180°-∠BAC=90°.
∵EF=AB=3,OA=OF=AC=2,
∴在Rt△OEF中,OE==.
∴DO=OE=.
14.(1)证明:∵AE⊥BD,AE平分∠BAC,
∴易得△ABE≌△ADE(ASA).
∴AB=AD,BE=DE.
∵点F是BC的中点,
∴EF=DC=(AC-AD)=(AC-AB).
(2)解:EF=(AB-AC).理由如下:
如图②,延长AC交BE的延长线于点P.
∵AE⊥BP,AE平分∠BAC,
∴易得△ABE≌△APE(ASA).
∴AB=AP,BE=PE.
∵点F是BC的中点,
∴EF=PC=(AP-AC)=(AB-AC).
