5.3平行线的性质 同步练习 2023-—2024学年人教版数学七年级下册(含答案)
文档属性
| 名称 | 5.3平行线的性质 同步练习 2023-—2024学年人教版数学七年级下册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 162.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-29 11:16:53 | ||
图片预览



文档简介
5.3平行线的性质 同步练习
一.选择题(共12小题)
1.甲、乙、丙三个学生分别在A、B、C三所大学学习数学、物理、化学中的一个专业,若已知:①甲不在A校学习;②乙不在B校学习;③在B校学习的学数学;④在A校学习的不学化学;⑤乙不学物理,则( )
A.甲在B校学习,丙在A校学习
B.甲在B校学习,丙在C校学习
C.甲在C校学习,丙在B校学习
D.甲在C校学习,丙在A校学习
2.在第36届全国中学生物理竞赛决赛中,华师一物理竞赛团队有5位同学获金牌,并全部进入国家集训队.五位同学猜谁是第一名,A说:是B,B说:是D,C说:是A,D说:B说错了,E说:不是我.教练说:你们中只有一人说对了,那么第一名是( )
A.B B.C C.D D.E
3.某届世界杯的小组比赛规则:四个球队进行单循环比赛(每两队赛一场),胜一场得3分,平一场得1分,负一场得0分,某小组比赛结束后,甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,打赢丁的球队是( )
A.乙与丙 B.甲与乙 C.甲与丙 D.不能确定
4.下列四个命题中,真命题有( )
①两条直线被第三条直线所截,同位角相等;
②实数与数轴上的点是一一对应的;
③三角形的一个外角大于任何一个内角;
④平面内点A(﹣1,2)与点B(﹣1,﹣2)关于x轴对称.
A.1个 B.2个 C.3个 D.4个
5.下列语句是命题的是( )
A.作直线AB的垂线 B.同旁内角互补
C.在线段AB上取点C D.垂线段最短吗?
6.下列命题的逆命题成立的是( )
A.全等三角形的对应角相等
B.如果两个数相等,那么它们的绝对值相等
C.对顶角相等
D.线段的垂直平分线上的点到线段两端的距离相等
7.对于下列的叙述,其中不正确的是( )
A.两直线平行,同旁内角互补
B.同位角相等,两直线平行
C.过一点有且只有一条直线与已知直线平行
D.两点之间的所有连线中,线段最短
8.如图,AB∥CD,∠BAE=∠DCE=45°,求∠E的度数,下面为解答过程:
解:∵AB∥CD,
∴∠1+45°+∠2+45°=①,(依据②)
∴∠1+∠2=③,∴∠E=④
则下列说法正确的是( )
A.①是90°
B.②是同旁内角是互补,两直线平行
C.③是180°
D.④是90°
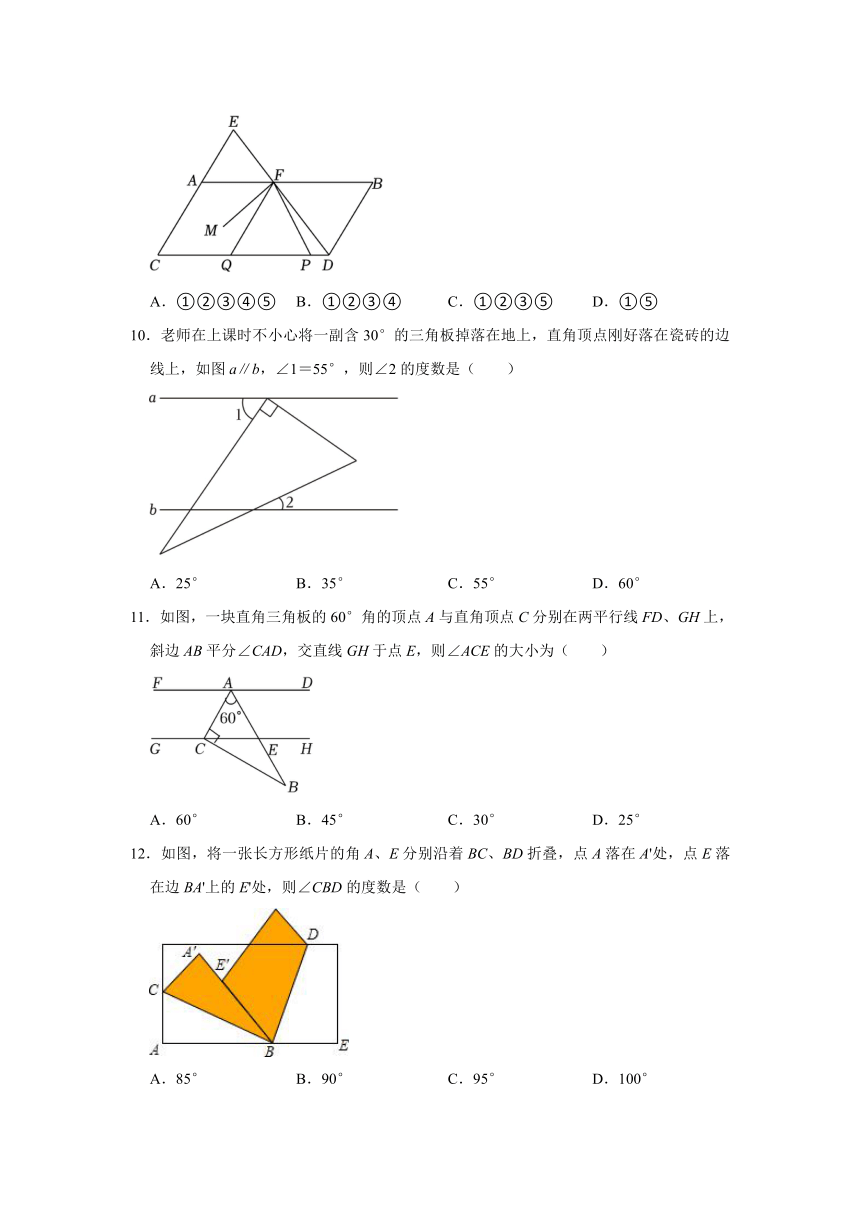
9.如图,点E在CA延长线上,DE,AB交于点F,且∠BDE=∠AEF,∠B=∠C,∠EFA比∠FDC的余角大30°,P为线段DC上一动点,Q为PC上一点,且满足∠FQP=∠QFP,FM为∠EFP的平分线.下列结论:
①CE∥BD;
②AB∥CD;
③FQ平分∠AFP;
④∠B+∠E=140°;
⑤∠QFM=30°.其中结论正确的序号是( )
A.①②③④⑤ B.①②③④ C.①②③⑤ D.①⑤
10.老师在上课时不小心将一副含30°的三角板掉落在地上,直角顶点刚好落在瓷砖的边线上,如图a∥b,∠1=55°,则∠2的度数是( )
A.25° B.35° C.55° D.60°
11.如图,一块直角三角板的60°角的顶点A与直角顶点C分别在两平行线FD、GH上,斜边AB平分∠CAD,交直线GH于点E,则∠ACE的大小为( )
A.60° B.45° C.30° D.25°
12.如图,将一张长方形纸片的角A、E分别沿着BC、BD折叠,点A落在A'处,点E落在边BA'上的E'处,则∠CBD的度数是( )
A.85° B.90° C.95° D.100°
二.填空题(共6小题)
13.命题“等角的余角相等”是 命题.(填“真”或“假”)
14.为响应国家新能源建设,某市公交站亭装上了太阳能电池板.当地某一季节的太阳光(平行光线)与水平线最大夹角为68°,如图,电池板AB与最大夹角时刻的太阳光线相垂直,此时电池板CD与水平线夹角为43°,要使AB∥CD,需将电池板CD逆时针旋转α(0<α<90)度,则α为 .
15.如图1是某景区电动升降门,将其抽象为几何图形,如图2所示,BA垂直于地面AE于A,当CD平行于地面AE时,则∠ABC+∠BCD= .
16.如图,点E在CA的延长线上,DE与AB交于点F,且∠BDE=∠AEF,∠B=∠C,∠EFA=35°,P为线段DC上一动点,Q为PC上一点,且满足∠FQP=∠QFP,FM为∠EFP的平分线.下列结论:①CE∥BD;②FQ平分∠AFP;③∠B+∠E=135°;④∠QFM=17.5°.其中结论正确的有 (填写所有正确结论的序号).
17.如图,是某剧场第一排座位分布图.甲、乙、丙、丁四人购票,所购票数分别为1,3,5,6.每人选座购票时,只购买第一排的座位相邻的票,同时使自己所选的座位之和最小.如果按“甲、乙、丙、丁”的先后顺序购票,那么甲购买1号座位的票,乙购买2,4,6号座位的票,丙购买3,5,7,9,11号座位的票,丁无法购买到第一排座位的票.若让丙第一购票,要使其他三人都能购买到第一排座位的票,写出满足条件的丁所选座位号之和为 .
三.解答题(共4小题)
18.如图,已知∠1+∠2=180°,且∠3=∠B,
(1)试说明:∠AFE=∠ACB;
(2)若CE平分∠ACB,且∠1=85°,∠3=50°,求∠AFE的度数.
19.完成下面推理过程:
已知:如图,已知AB⊥AC,DE⊥AC,∠B=∠D.
求证:AD∥BC.
证明:∵AB⊥AC,DE⊥AC,(已知)
∴ ∥ .(在同一平面内,垂直于同一条直线的两条直线平行.)
∴∠B=∠DEC.( )
又∵∠B=∠D,(已知)
∴∠D= .(等量代换)
∴AD∥BC.( )
20.已知命题“如果a=b,那么|a|=|b|.”
(1)写出此命题的条件和结论;
(2)写出此命题的逆命题;
(3)判断此命题的逆命题是真命题还是假命题,如果是假命题,请举出一个反例进行说明.
21.生活中的说理
小明、小红、小丽三人中一个是班长,一个是学习委员,一个是生活委员.现在知道小红比生活委员年龄大,小明与学习委员不同岁,学习委员比小丽年龄小.请你猜一猜他们当中谁是班长,并说明理由.
22.如图,已知AB∥CD,BE平分∠ABC.BE垂直于CE,求证:CE平分∠BCD.
参考答案
一.选择题(共12小题)
1--10ADCBB DCDCA 11--12AB
二.填空题(共6小题)
13.真
14.21
15.270°
16.①②④
17.66.
三.解答题(共4小题)
18.(1)证明:∵∠1+∠2=180°,∠1+∠FDE=180°,
∴∠FDE=∠2,
∵∠3+∠FEC+∠FDE=180°,∠2+∠B+∠ECB=180°,∠B=∠3,
∴∠FEC=∠ECB,
∴EF∥BC,
∴∠AFE=∠ACB;
(2)解:∵∠1=85°,∠3=50°,
∴∠FEC=∠1﹣∠3=35°,
∵∠FEC=∠ECB,
∴∠ECB=35°,
∵CE平分∠ACB,
∴∠ACB=2∠ECB=70°,
∴∠AFE=∠ACB=70°.
19.证明:∵AB⊥AC,DE⊥AC,(已知)
∴AB∥DE.(在同一平面内,垂直于同一条直线的两条直线平行.)
∴∠B=∠DEC.(两直线平行,同位角相等.)
又∵∠B=∠D,(已知)
∴∠D=∠DEC.(等量代换)
∴AD∥BC.(内错角相等,两直线平行.)
故答案为:AB;DE;两直线平行,同位角相等;∠DEC;内错角相等,两直线平行.
20.解:(1)此命题的条件为:a=b,
结论为:|a|=|b|;
(2)此命题的逆命题为:如果|a|=|b|,那么a=b;
(3)此命题的逆命题是假命题,
当a,b为相反数时,它们的绝对值相等,但本身不相等,
如a=2,b=﹣2时,|2|=|﹣2|,而2≠﹣2.
21.解:小丽是班长,
理由:由小明与学习委员不同岁,可得小明非学习委员,则是班长或者生活委员;
由学习委员比小丽年龄小,可得小丽非学习委员,则是班长或者生活委员;
由小红比生活委员年龄大,可得小红是学习委员,
由年龄可以判断小丽是班长.
22.证明:过E作EF∥AB 交BC于点F,
∴∠ABE=∠FEB,
∵AB∥CD,
∴EF∥CD,∠ABC+∠BCD=180°,
∴∠DCE=∠FEC,
∵BE⊥CE,
∴∠BEF+∠CEF=∠ABE+∠DCE=90°,
∴∠EBC+∠ECB=90°,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠DCE=∠BCE,
∴CE平分∠BCD.
一.选择题(共12小题)
1.甲、乙、丙三个学生分别在A、B、C三所大学学习数学、物理、化学中的一个专业,若已知:①甲不在A校学习;②乙不在B校学习;③在B校学习的学数学;④在A校学习的不学化学;⑤乙不学物理,则( )
A.甲在B校学习,丙在A校学习
B.甲在B校学习,丙在C校学习
C.甲在C校学习,丙在B校学习
D.甲在C校学习,丙在A校学习
2.在第36届全国中学生物理竞赛决赛中,华师一物理竞赛团队有5位同学获金牌,并全部进入国家集训队.五位同学猜谁是第一名,A说:是B,B说:是D,C说:是A,D说:B说错了,E说:不是我.教练说:你们中只有一人说对了,那么第一名是( )
A.B B.C C.D D.E
3.某届世界杯的小组比赛规则:四个球队进行单循环比赛(每两队赛一场),胜一场得3分,平一场得1分,负一场得0分,某小组比赛结束后,甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,打赢丁的球队是( )
A.乙与丙 B.甲与乙 C.甲与丙 D.不能确定
4.下列四个命题中,真命题有( )
①两条直线被第三条直线所截,同位角相等;
②实数与数轴上的点是一一对应的;
③三角形的一个外角大于任何一个内角;
④平面内点A(﹣1,2)与点B(﹣1,﹣2)关于x轴对称.
A.1个 B.2个 C.3个 D.4个
5.下列语句是命题的是( )
A.作直线AB的垂线 B.同旁内角互补
C.在线段AB上取点C D.垂线段最短吗?
6.下列命题的逆命题成立的是( )
A.全等三角形的对应角相等
B.如果两个数相等,那么它们的绝对值相等
C.对顶角相等
D.线段的垂直平分线上的点到线段两端的距离相等
7.对于下列的叙述,其中不正确的是( )
A.两直线平行,同旁内角互补
B.同位角相等,两直线平行
C.过一点有且只有一条直线与已知直线平行
D.两点之间的所有连线中,线段最短
8.如图,AB∥CD,∠BAE=∠DCE=45°,求∠E的度数,下面为解答过程:
解:∵AB∥CD,
∴∠1+45°+∠2+45°=①,(依据②)
∴∠1+∠2=③,∴∠E=④
则下列说法正确的是( )
A.①是90°
B.②是同旁内角是互补,两直线平行
C.③是180°
D.④是90°
9.如图,点E在CA延长线上,DE,AB交于点F,且∠BDE=∠AEF,∠B=∠C,∠EFA比∠FDC的余角大30°,P为线段DC上一动点,Q为PC上一点,且满足∠FQP=∠QFP,FM为∠EFP的平分线.下列结论:
①CE∥BD;
②AB∥CD;
③FQ平分∠AFP;
④∠B+∠E=140°;
⑤∠QFM=30°.其中结论正确的序号是( )
A.①②③④⑤ B.①②③④ C.①②③⑤ D.①⑤
10.老师在上课时不小心将一副含30°的三角板掉落在地上,直角顶点刚好落在瓷砖的边线上,如图a∥b,∠1=55°,则∠2的度数是( )
A.25° B.35° C.55° D.60°
11.如图,一块直角三角板的60°角的顶点A与直角顶点C分别在两平行线FD、GH上,斜边AB平分∠CAD,交直线GH于点E,则∠ACE的大小为( )
A.60° B.45° C.30° D.25°
12.如图,将一张长方形纸片的角A、E分别沿着BC、BD折叠,点A落在A'处,点E落在边BA'上的E'处,则∠CBD的度数是( )
A.85° B.90° C.95° D.100°
二.填空题(共6小题)
13.命题“等角的余角相等”是 命题.(填“真”或“假”)
14.为响应国家新能源建设,某市公交站亭装上了太阳能电池板.当地某一季节的太阳光(平行光线)与水平线最大夹角为68°,如图,电池板AB与最大夹角时刻的太阳光线相垂直,此时电池板CD与水平线夹角为43°,要使AB∥CD,需将电池板CD逆时针旋转α(0<α<90)度,则α为 .
15.如图1是某景区电动升降门,将其抽象为几何图形,如图2所示,BA垂直于地面AE于A,当CD平行于地面AE时,则∠ABC+∠BCD= .
16.如图,点E在CA的延长线上,DE与AB交于点F,且∠BDE=∠AEF,∠B=∠C,∠EFA=35°,P为线段DC上一动点,Q为PC上一点,且满足∠FQP=∠QFP,FM为∠EFP的平分线.下列结论:①CE∥BD;②FQ平分∠AFP;③∠B+∠E=135°;④∠QFM=17.5°.其中结论正确的有 (填写所有正确结论的序号).
17.如图,是某剧场第一排座位分布图.甲、乙、丙、丁四人购票,所购票数分别为1,3,5,6.每人选座购票时,只购买第一排的座位相邻的票,同时使自己所选的座位之和最小.如果按“甲、乙、丙、丁”的先后顺序购票,那么甲购买1号座位的票,乙购买2,4,6号座位的票,丙购买3,5,7,9,11号座位的票,丁无法购买到第一排座位的票.若让丙第一购票,要使其他三人都能购买到第一排座位的票,写出满足条件的丁所选座位号之和为 .
三.解答题(共4小题)
18.如图,已知∠1+∠2=180°,且∠3=∠B,
(1)试说明:∠AFE=∠ACB;
(2)若CE平分∠ACB,且∠1=85°,∠3=50°,求∠AFE的度数.
19.完成下面推理过程:
已知:如图,已知AB⊥AC,DE⊥AC,∠B=∠D.
求证:AD∥BC.
证明:∵AB⊥AC,DE⊥AC,(已知)
∴ ∥ .(在同一平面内,垂直于同一条直线的两条直线平行.)
∴∠B=∠DEC.( )
又∵∠B=∠D,(已知)
∴∠D= .(等量代换)
∴AD∥BC.( )
20.已知命题“如果a=b,那么|a|=|b|.”
(1)写出此命题的条件和结论;
(2)写出此命题的逆命题;
(3)判断此命题的逆命题是真命题还是假命题,如果是假命题,请举出一个反例进行说明.
21.生活中的说理
小明、小红、小丽三人中一个是班长,一个是学习委员,一个是生活委员.现在知道小红比生活委员年龄大,小明与学习委员不同岁,学习委员比小丽年龄小.请你猜一猜他们当中谁是班长,并说明理由.
22.如图,已知AB∥CD,BE平分∠ABC.BE垂直于CE,求证:CE平分∠BCD.
参考答案
一.选择题(共12小题)
1--10ADCBB DCDCA 11--12AB
二.填空题(共6小题)
13.真
14.21
15.270°
16.①②④
17.66.
三.解答题(共4小题)
18.(1)证明:∵∠1+∠2=180°,∠1+∠FDE=180°,
∴∠FDE=∠2,
∵∠3+∠FEC+∠FDE=180°,∠2+∠B+∠ECB=180°,∠B=∠3,
∴∠FEC=∠ECB,
∴EF∥BC,
∴∠AFE=∠ACB;
(2)解:∵∠1=85°,∠3=50°,
∴∠FEC=∠1﹣∠3=35°,
∵∠FEC=∠ECB,
∴∠ECB=35°,
∵CE平分∠ACB,
∴∠ACB=2∠ECB=70°,
∴∠AFE=∠ACB=70°.
19.证明:∵AB⊥AC,DE⊥AC,(已知)
∴AB∥DE.(在同一平面内,垂直于同一条直线的两条直线平行.)
∴∠B=∠DEC.(两直线平行,同位角相等.)
又∵∠B=∠D,(已知)
∴∠D=∠DEC.(等量代换)
∴AD∥BC.(内错角相等,两直线平行.)
故答案为:AB;DE;两直线平行,同位角相等;∠DEC;内错角相等,两直线平行.
20.解:(1)此命题的条件为:a=b,
结论为:|a|=|b|;
(2)此命题的逆命题为:如果|a|=|b|,那么a=b;
(3)此命题的逆命题是假命题,
当a,b为相反数时,它们的绝对值相等,但本身不相等,
如a=2,b=﹣2时,|2|=|﹣2|,而2≠﹣2.
21.解:小丽是班长,
理由:由小明与学习委员不同岁,可得小明非学习委员,则是班长或者生活委员;
由学习委员比小丽年龄小,可得小丽非学习委员,则是班长或者生活委员;
由小红比生活委员年龄大,可得小红是学习委员,
由年龄可以判断小丽是班长.
22.证明:过E作EF∥AB 交BC于点F,
∴∠ABE=∠FEB,
∵AB∥CD,
∴EF∥CD,∠ABC+∠BCD=180°,
∴∠DCE=∠FEC,
∵BE⊥CE,
∴∠BEF+∠CEF=∠ABE+∠DCE=90°,
∴∠EBC+∠ECB=90°,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠DCE=∠BCE,
∴CE平分∠BCD.
