第五章 基本平面图形 章末复习(含答案)
文档属性
| 名称 | 第五章 基本平面图形 章末复习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-27 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第五章 基本平面图形
章末复习
考点① 线段、射线、直线的有关知识
1.下列说法正确的是( )
A.两点之间的距离是两点间的直线长度 B.线段没有延长线
C.两点之间线段最短 D.直线有无数个端点
2.如图,AE 是一段高铁行驶路线图,图中字母表示的5个点表示5个车站,在这段路线上往返行车,需印制车票的数量是 ( )
A.10 B.11 C.18 D.20
3.数轴上表示整数的点称为整点,某数轴的单位长度是 1厘米,若在这个数轴上随意画出一条长 2 024 厘米的线段 AB,则线段 AB盖住的整点共有 ( )
A.2025个或2026个 B.2024 个或2025个
C.2023个或2024个 D.2022 个或2023 个
4.如图,小亮为将一个衣架固定在墙上,他在衣架两端各用一个钉子进行固定,用数学知识解释他这样操作的原因,应该是 ( )
A.过一点有无数条直线 B.两点之间线段的长度,叫做这两点之间的距离
C.两点确定一条直线 D.两点之间,线段最短
5.如图,点A,B,C在同一平面内,利用尺规,按下列要求作图.(不写作法,保留作图痕迹)
(1)画射线 AB 和线段 AC;
(2)在射线 AB 上求作一 点 P,使 2AC.
考点② 角的有关知识
6.用度,分,秒表示: 为___________.
7.8时20 分时,时针和分针的夹角的度数是___________.
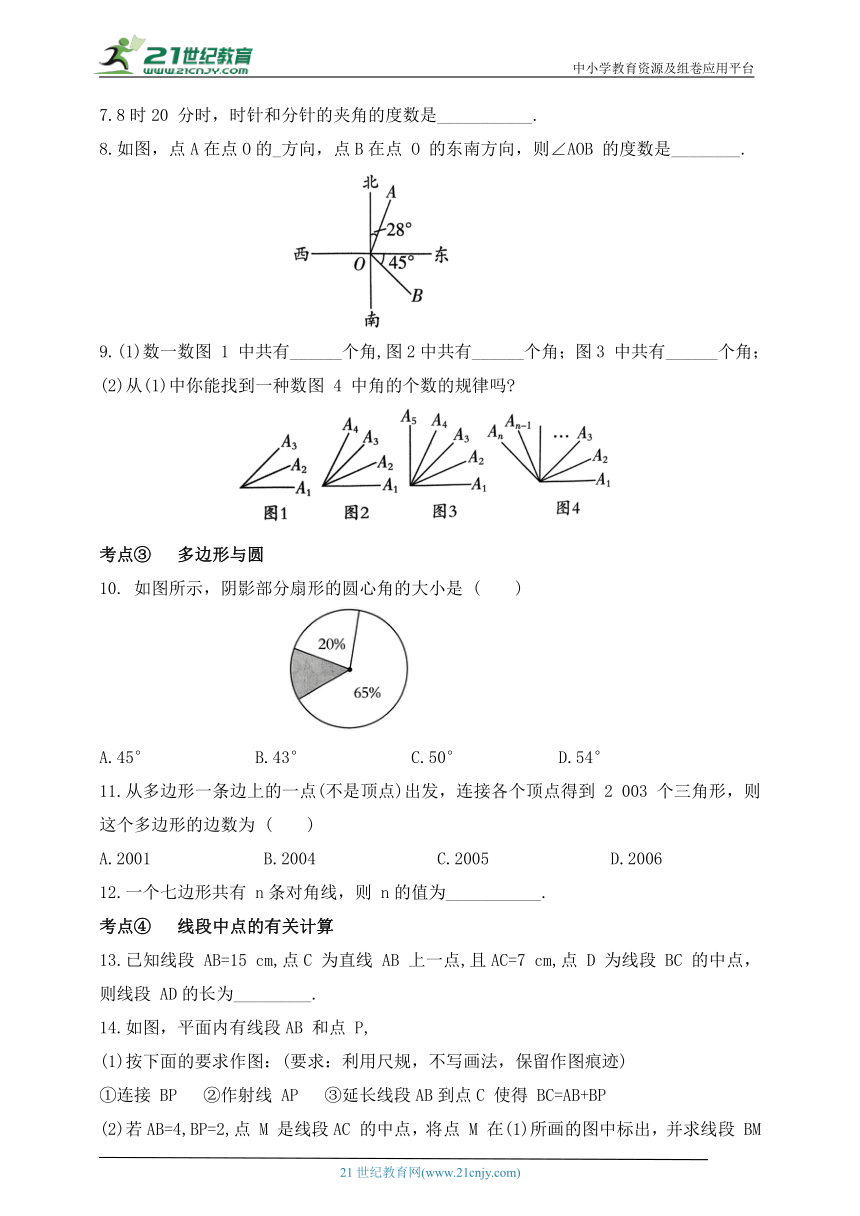
8.如图,点A在点O的_方向,点B在点 O 的东南方向,则∠AOB 的度数是________.
9.(1)数一数图 1 中共有______个角,图2中共有______个角;图3 中共有______个角;
(2)从(1)中你能找到一种数图 4 中角的个数的规律吗
考点③ 多边形与圆
10. 如图所示,阴影部分扇形的圆心角的大小是 ( )
A.45° B.43° C.50° D.54°
11.从多边形一条边上的一点(不是顶点)出发,连接各个顶点得到 2 003 个三角形,则这个多边形的边数为 ( )
A.2001 B.2004 C.2005 D.2006
12.一个七边形共有 n条对角线,则 n的值为___________.
考点④ 线段中点的有关计算
13.已知线段 AB=15 cm,点C 为直线 AB 上一点,且AC=7 cm,点 D 为线段 BC 的中点,则线段 AD的长为_________.
14.如图,平面内有线段AB 和点 P,
(1)按下面的要求作图:(要求:利用尺规,不写画法,保留作图痕迹)
①连接 BP ②作射线 AP ③延长线段AB到点C 使得 BC=AB+BP
(2)若AB=4,BP=2,点 M 是线段AC 的中点,将点 M 在(1)所画的图中标出,并求线段 BM的长.
15.如图,点 P 是线段AB 上一点, C,D两动点分别从点 P,B同时出发沿射线 BA 向左运动,到达点 A 处即停止运动.
(1)若点 C,D的速度分别是
①当动点C,D运动了 2s,且点 D 仍在线段 PB 上时,
②若点C到达AP 中点时,点 D 也刚好到达 BP 的中点,则
(2)若动点 C,D 的速度分别是 1 cm/s,3c m/s,点 C,D在运动,且点 D 始终在线段 PB 上时,总有 PD=3AC,求 AP 的长.
考点⑤ 角平分线的有关计算
16.如图,已知直线 AB 与CD 相交于点O,OE 是∠BOC 的平分线,如果∠BOC:∠DOF:∠AOC=1:2:4.求∠EOF 的度数.
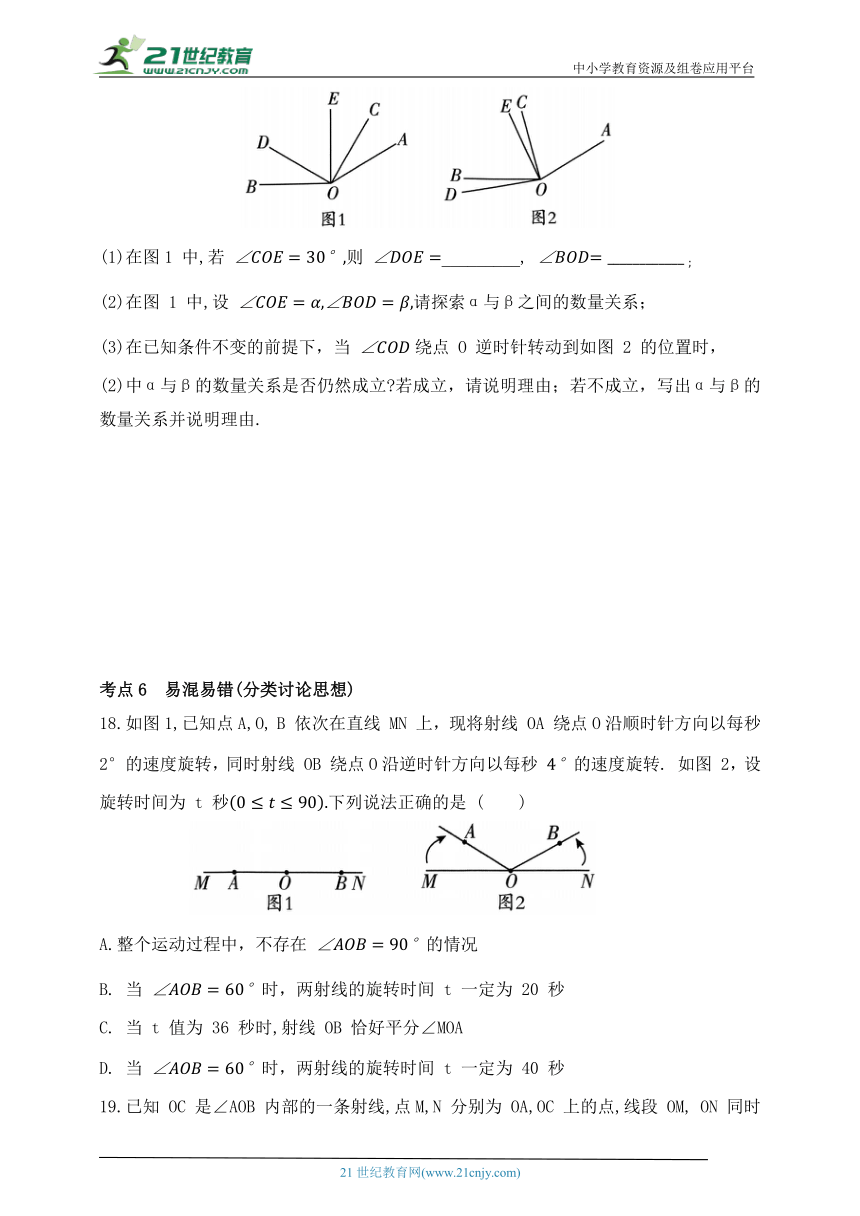
17.如图 1,已知 OE 平分
(1)在图1 中,若 则 _________,
(2)在图 1 中,设 请探索α与β之间的数量关系;
(3)在已知条件不变的前提下,当 绕点 O 逆时针转动到如图 2 的位置时,
(2)中α与β的数量关系是否仍然成立 若成立,请说明理由;若不成立,写出α与β的数量关系并说明理由.
考点6 易混易错(分类讨论思想)
18.如图1,已知点A,O, B 依次在直线 MN 上,现将射线 OA 绕点O沿顺时针方向以每秒2°的速度旋转,同时射线 OB 绕点O沿逆时针方向以每秒 的速度旋转. 如图 2,设旋转时间为 t 秒下列说法正确的是 ( )
A.整个运动过程中,不存在 的情况
B. 当 时,两射线的旋转时间 t 一定为 20 秒
C. 当 t 值为 36 秒时,射线 OB 恰好平分∠MOA
D. 当 时,两射线的旋转时间 t 一定为 40 秒
19.已知 OC 是∠AOB 内部的一条射线,点M,N 分别为 OA,OC 上的点,线段 OM, ON 同时分别以每秒 30°、每秒 10°的速度绕点 O逆时针转动,当OM,ON逆时针转动到OM',ON'处,设转动时间为 t秒(
(1)如图 1, 若 OM,ON 转动时间 t =2 时,则 _________°;
(2)若
①当 时,求转动时间 t的值;
②当 时,求转动时间t的值.
参考答案
C 2. D 3. B 4. C
5.解:(1)射线 AB 和线段 AC,如图所示:
(2)点 P 如图所示:
130°
北偏东
9.解:(1)因为 则图①中共有个角,,则图②中共有6个角,
则图③中共有 10个角.故答案为:3 6 10;
(2)因为
所以图④中共有
10. D 11. B 12.14
13.4 cm 或 11 cm
14.解:(1)如图1所示,线段 BP,射线 AP,线段BC即为所求;
(2)如图 2所示:
因为 AB=4,BP=2,所以 AC=AB+BC=AB+AB+BP=2AB+BP=2×4+2=10,
因为点 M是线段AC 的中点,所以 所以BM=AM-AB=5-4=1.
15.解:(1)①由题意得 2×2=4(cm),
因为 AB=18cm,点 D仍在线段 PB上,所以 AC+PD=AB-PC-BD=18-2-4=12(cm),
故答案为:12;
②设 运动 时间 为 ts,则 PC=t cm, BD=2t cm,
因为当点 C到达 AP 中点时,点 D 也刚好到达 BP的中点,
所以AP=2PC=2t cm,BP=2BD=4t cm,所以 AP:PB=1:2,
故答案为:1:2;
(2)设运动时间为 xs,则 PC=x cm,BD=3x cm,所以 BD=3PC,
因为 PD=3AC,所以PB=BD+PD=3PC+3AC=3(PC+AC)=3AP,
因为 PB+AP=AB,所以 3AP+AP=AB,所以
16.解:设∠BOC=x°,则∠DOF=2x°,∠AOC=4x°,
由题意,得x+4x=180,解得 x=36,所以∠BOC=36°,∠DOF=72°,
因为OE 是∠BOC的平分线,所以 36°=18°.
所以∠EOF =180°-∠DOF-∠COE=180°-72°-18°=90°.
17.解:(1)因为∠COE=30°,则∠DOE=90°一∠COE=90°-30°=60°,
因为OE平分∠AOD,所以∠AOE=∠DOE=60°,所以∠AOD=120°
所以∠BOD=∠AOB-∠AOD=150°-120°=30°;
故答案为:60° 30°;
(2)因为∠COE+∠EOD=90°,所以∠DOE=90°-∠COE=90°-α,
因为 OE 平分∠AOD,所以∠AOD=2∠DOE=2(90°-α),
因为∠AOB=150°,∠BOD=β,所以2(90°-α)+β=150°,
整理得 2α-β=30°;
(3)因为∠COE+∠EOD=90°,所以∠DOE=90°-∠COE=90°-α,
因为 OE 平分 ∠AOD,所以∠AOD=2∠DOE=2(90°-α),
因为∠AOB=150°,∠BOD=β,所以 2(90°-α)-150°=β,
整理得 2a+β=30°.
18. C
19.解:(1)由题意得 ∠NON'=10°×2=20°,∠MOM'=30°×2=60°,
则∠BON'=∠BOC-∠NON'=∠BOC-20°,
所以
故答案为:
(2)①当( 与 重合之前时,解得
当 与 重合之后时, 解得
故转动的时间 或
②当 与OC 重合之前, 解得
当 与 重合时, 解得
故转动的时间 或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 基本平面图形
章末复习
考点① 线段、射线、直线的有关知识
1.下列说法正确的是( )
A.两点之间的距离是两点间的直线长度 B.线段没有延长线
C.两点之间线段最短 D.直线有无数个端点
2.如图,AE 是一段高铁行驶路线图,图中字母表示的5个点表示5个车站,在这段路线上往返行车,需印制车票的数量是 ( )
A.10 B.11 C.18 D.20
3.数轴上表示整数的点称为整点,某数轴的单位长度是 1厘米,若在这个数轴上随意画出一条长 2 024 厘米的线段 AB,则线段 AB盖住的整点共有 ( )
A.2025个或2026个 B.2024 个或2025个
C.2023个或2024个 D.2022 个或2023 个
4.如图,小亮为将一个衣架固定在墙上,他在衣架两端各用一个钉子进行固定,用数学知识解释他这样操作的原因,应该是 ( )
A.过一点有无数条直线 B.两点之间线段的长度,叫做这两点之间的距离
C.两点确定一条直线 D.两点之间,线段最短
5.如图,点A,B,C在同一平面内,利用尺规,按下列要求作图.(不写作法,保留作图痕迹)
(1)画射线 AB 和线段 AC;
(2)在射线 AB 上求作一 点 P,使 2AC.
考点② 角的有关知识
6.用度,分,秒表示: 为___________.
7.8时20 分时,时针和分针的夹角的度数是___________.
8.如图,点A在点O的_方向,点B在点 O 的东南方向,则∠AOB 的度数是________.
9.(1)数一数图 1 中共有______个角,图2中共有______个角;图3 中共有______个角;
(2)从(1)中你能找到一种数图 4 中角的个数的规律吗
考点③ 多边形与圆
10. 如图所示,阴影部分扇形的圆心角的大小是 ( )
A.45° B.43° C.50° D.54°
11.从多边形一条边上的一点(不是顶点)出发,连接各个顶点得到 2 003 个三角形,则这个多边形的边数为 ( )
A.2001 B.2004 C.2005 D.2006
12.一个七边形共有 n条对角线,则 n的值为___________.
考点④ 线段中点的有关计算
13.已知线段 AB=15 cm,点C 为直线 AB 上一点,且AC=7 cm,点 D 为线段 BC 的中点,则线段 AD的长为_________.
14.如图,平面内有线段AB 和点 P,
(1)按下面的要求作图:(要求:利用尺规,不写画法,保留作图痕迹)
①连接 BP ②作射线 AP ③延长线段AB到点C 使得 BC=AB+BP
(2)若AB=4,BP=2,点 M 是线段AC 的中点,将点 M 在(1)所画的图中标出,并求线段 BM的长.
15.如图,点 P 是线段AB 上一点, C,D两动点分别从点 P,B同时出发沿射线 BA 向左运动,到达点 A 处即停止运动.
(1)若点 C,D的速度分别是
①当动点C,D运动了 2s,且点 D 仍在线段 PB 上时,
②若点C到达AP 中点时,点 D 也刚好到达 BP 的中点,则
(2)若动点 C,D 的速度分别是 1 cm/s,3c m/s,点 C,D在运动,且点 D 始终在线段 PB 上时,总有 PD=3AC,求 AP 的长.
考点⑤ 角平分线的有关计算
16.如图,已知直线 AB 与CD 相交于点O,OE 是∠BOC 的平分线,如果∠BOC:∠DOF:∠AOC=1:2:4.求∠EOF 的度数.
17.如图 1,已知 OE 平分
(1)在图1 中,若 则 _________,
(2)在图 1 中,设 请探索α与β之间的数量关系;
(3)在已知条件不变的前提下,当 绕点 O 逆时针转动到如图 2 的位置时,
(2)中α与β的数量关系是否仍然成立 若成立,请说明理由;若不成立,写出α与β的数量关系并说明理由.
考点6 易混易错(分类讨论思想)
18.如图1,已知点A,O, B 依次在直线 MN 上,现将射线 OA 绕点O沿顺时针方向以每秒2°的速度旋转,同时射线 OB 绕点O沿逆时针方向以每秒 的速度旋转. 如图 2,设旋转时间为 t 秒下列说法正确的是 ( )
A.整个运动过程中,不存在 的情况
B. 当 时,两射线的旋转时间 t 一定为 20 秒
C. 当 t 值为 36 秒时,射线 OB 恰好平分∠MOA
D. 当 时,两射线的旋转时间 t 一定为 40 秒
19.已知 OC 是∠AOB 内部的一条射线,点M,N 分别为 OA,OC 上的点,线段 OM, ON 同时分别以每秒 30°、每秒 10°的速度绕点 O逆时针转动,当OM,ON逆时针转动到OM',ON'处,设转动时间为 t秒(
(1)如图 1, 若 OM,ON 转动时间 t =2 时,则 _________°;
(2)若
①当 时,求转动时间 t的值;
②当 时,求转动时间t的值.
参考答案
C 2. D 3. B 4. C
5.解:(1)射线 AB 和线段 AC,如图所示:
(2)点 P 如图所示:
130°
北偏东
9.解:(1)因为 则图①中共有个角,,则图②中共有6个角,
则图③中共有 10个角.故答案为:3 6 10;
(2)因为
所以图④中共有
10. D 11. B 12.14
13.4 cm 或 11 cm
14.解:(1)如图1所示,线段 BP,射线 AP,线段BC即为所求;
(2)如图 2所示:
因为 AB=4,BP=2,所以 AC=AB+BC=AB+AB+BP=2AB+BP=2×4+2=10,
因为点 M是线段AC 的中点,所以 所以BM=AM-AB=5-4=1.
15.解:(1)①由题意得 2×2=4(cm),
因为 AB=18cm,点 D仍在线段 PB上,所以 AC+PD=AB-PC-BD=18-2-4=12(cm),
故答案为:12;
②设 运动 时间 为 ts,则 PC=t cm, BD=2t cm,
因为当点 C到达 AP 中点时,点 D 也刚好到达 BP的中点,
所以AP=2PC=2t cm,BP=2BD=4t cm,所以 AP:PB=1:2,
故答案为:1:2;
(2)设运动时间为 xs,则 PC=x cm,BD=3x cm,所以 BD=3PC,
因为 PD=3AC,所以PB=BD+PD=3PC+3AC=3(PC+AC)=3AP,
因为 PB+AP=AB,所以 3AP+AP=AB,所以
16.解:设∠BOC=x°,则∠DOF=2x°,∠AOC=4x°,
由题意,得x+4x=180,解得 x=36,所以∠BOC=36°,∠DOF=72°,
因为OE 是∠BOC的平分线,所以 36°=18°.
所以∠EOF =180°-∠DOF-∠COE=180°-72°-18°=90°.
17.解:(1)因为∠COE=30°,则∠DOE=90°一∠COE=90°-30°=60°,
因为OE平分∠AOD,所以∠AOE=∠DOE=60°,所以∠AOD=120°
所以∠BOD=∠AOB-∠AOD=150°-120°=30°;
故答案为:60° 30°;
(2)因为∠COE+∠EOD=90°,所以∠DOE=90°-∠COE=90°-α,
因为 OE 平分∠AOD,所以∠AOD=2∠DOE=2(90°-α),
因为∠AOB=150°,∠BOD=β,所以2(90°-α)+β=150°,
整理得 2α-β=30°;
(3)因为∠COE+∠EOD=90°,所以∠DOE=90°-∠COE=90°-α,
因为 OE 平分 ∠AOD,所以∠AOD=2∠DOE=2(90°-α),
因为∠AOB=150°,∠BOD=β,所以 2(90°-α)-150°=β,
整理得 2a+β=30°.
18. C
19.解:(1)由题意得 ∠NON'=10°×2=20°,∠MOM'=30°×2=60°,
则∠BON'=∠BOC-∠NON'=∠BOC-20°,
所以
故答案为:
(2)①当( 与 重合之前时,解得
当 与 重合之后时, 解得
故转动的时间 或
②当 与OC 重合之前, 解得
当 与 重合时, 解得
故转动的时间 或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
