18.1平行四边形同步练习2023—2024学年人教版数学八年级下册(含答案)
文档属性
| 名称 | 18.1平行四边形同步练习2023—2024学年人教版数学八年级下册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 269.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-29 12:25:23 | ||
图片预览




文档简介
18.1平行四边形 同步练习
一.选择题(共12小题)
1.如图,在四边形ABCD中,对角线AC、BD相交于点O.下列条件不能判定四边形ABCD为平行四边形的是( )
A.AB∥CD,AD∥BC B.OA=OC,OB=OD
C.AB=CD,AD=BC D.AB∥CD,AD=BC
2.如图,a∥b,点A在直线a上,点B、C在直线b上,AC⊥b,如果AB=5cm,AC=4cm,那么平行线a、b之间的距离为( )
A.5cm B.4cm C.3cm D.不能确定
3.如图,在△ABC中,AB=8,∠C=90°,∠A=30°,DE是中位线,则DE的长为( )
A.2 B.3 C.4 D.2
4.如图所示,已知直线a∥b,点A,C,F在直线a上,点B,D,E,G在直线b上,且AB∥CD,CE⊥b,FG⊥b,则下列说法中不正确的有( )
①AB=FG;②A,B两点的距离就是线段AB的长,③EC=FG;④直线a,b的距离就是线段CD的长.
A.1个 B.2个 C.3个 D.4个
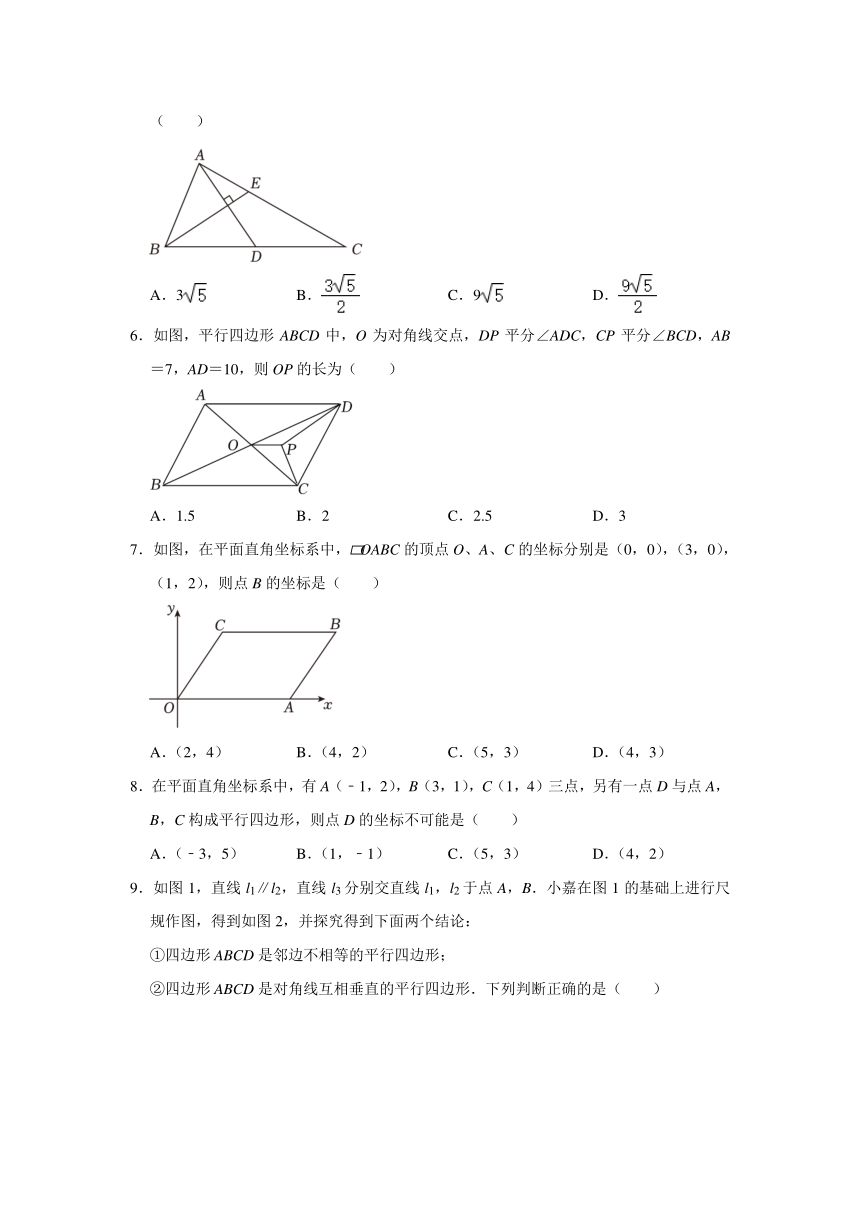
5.如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE=6,则AC的长为( )
A.3 B. C.9 D.
6.如图,平行四边形ABCD中,O为对角线交点,DP平分∠ADC,CP平分∠BCD,AB=7,AD=10,则OP的长为( )
A.1.5 B.2 C.2.5 D.3
7.如图,在平面直角坐标系中, OABC的顶点O、A、C的坐标分别是(0,0),(3,0),(1,2),则点B的坐标是( )
A.(2,4) B.(4,2) C.(5,3) D.(4,3)
8.在平面直角坐标系中,有A(﹣1,2),B(3,1),C(1,4)三点,另有一点D与点A,B,C构成平行四边形,则点D的坐标不可能是( )
A.(﹣3,5) B.(1,﹣1) C.(5,3) D.(4,2)
9.如图1,直线l1∥l2,直线l3分别交直线l1,l2于点A,B.小嘉在图1的基础上进行尺规作图,得到如图2,并探究得到下面两个结论:
①四边形ABCD是邻边不相等的平行四边形;
②四边形ABCD是对角线互相垂直的平行四边形.下列判断正确的是( )
A.①②都正确 B.①错误,②正确
C.①②都错误 D.①正确,②错误
10.如图,O是 ABCD对角线AC上一点,过O作EF∥AD交AB于点E,交CD于点F,GH∥AB交AD于点G,交BC于点H,连结GE,GF,HE,HF,若已知下列图形的面积,不能求出 ABCD面积的是( )
A.四边形EHFG
B.△AEG和△CHF
C.四边形EBHO和四边形GOFD
D.△AEO和四边形GOFD
11.如图,在平行四边形ABCD中,分别以AB、AD为边向外作等边△ABE和等边△ADF,延长CB交AE于点G,点G在点A、E之间,连接CE、CF、EF,则以下四个结论,正确的是( )
①△CDF≌△EBC;②∠CDF=∠EAF;③CG⊥AE;④△CEF是等边三角形.
A.③④ B.①②④ C.①②③ D.①②③④
12.如图,在平行四边形ABCD中,点F是BC上一点,BF=6,CF=2,点E是CD的中点,AE平分∠DAF,EF=,则△AEF的面积是( )
A. B. C. D.
二.填空题(共5小题)
13.如图,已知AD∥BC,CE=5,CF=8,且CE⊥AD,CF⊥AB垂足分别为E,F.则AD与BC间的距离是 .
14.如图,在△ABC中,点D、E分别是AB、AC的中点,点F在DE上,且AF⊥CF,若AC=3,BC=6,则DF的长为 .
15.如图,在四边形ABCD中,AD∥BC,BC=6厘米,AD=9厘米,P、Q分别从A、C同时出发,P以1厘米/秒的速度由A向D运动,Q以2厘米/秒的速度由C向B运动.设运动的时间为t秒,则当t= 时,直线PQ将四边形ABCD截出一个平行四边形.
16.如图,在 ABCD中,点F在边AD上,AF=2FD,直线BF与对角线AC相交于点E,交CD的延长线于点G,如果BE=2,那么EG的长是 .
17.如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了一个四边形.在转动其中一张纸条的过程中,线段AD和BC的长度始终相等,这里蕴含的数学原理是 .
三.解答题(共5小题)
18.如图,直线a∥b,AB与a,b分别相交于点A,B,且AC⊥AB,AC交直线b于点C.
(1)若∠1=58°,求∠2的度数;
(2)若AC=5,AB=12,BC=13,求直线a与b的距离.
19.求证:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
已知:如图,点D、E分别是△ABC的边AB、AC的中点,连接DE.
求证:DE∥BC,且DE=BC.
(要求:尺规作图画出D点和E点,只保留作图痕迹,不写作法)
20.如图, ABCD的对角线AC,BD相交于点O,点E,F在AC上,且AE=CF.
(1)求证:BE∥DF;
(2)过点O作OM⊥BD,垂足为O,交DF于点M,若△BFM的周长为12,求四边形BEDF的周长.
21.如图,点A(1,2),点B(2,0).求:
(1)求OA和AB的解析式;
(2)在坐标平面内存在一点C,使得以O、A、C、B为顶点的四边形为平行四边形,直接写出点C的坐标.
22.如图,在 ABCD中,分别过A,C两点作对角线BD的垂线,垂足分别为E,F.
求证:四边形AFCE是平行四边形.
参考答案
一.选择题(共12小题)
1--10DBABD ABDBC 11--12BD
二.填空题(共5小题)
13.5
14.1.5
15.2或3
16.3
故答案为:3.
17.平行四边形的对边相等.
三.解答题(共5小题)
18.解:(1)∵AC⊥AB,
∴∠BAC=90°,
∵∠1=58°,
∴∠ABC=90°﹣58°=32°,
∵a∥b,
∴∠2=∠ABC=32°;
(2)如图,过点A作AD⊥BC,垂足为D,
所以线段AD的长度等于a与b之间的距离,
因为AB⊥AC
所以AB AC=BC AD,
所以AD=,
所以a与b的距离为.
19.证明:分别作线段AB和线段AC的垂直平分线,交点分别为点D和E,延长DE到F,使EF=DE,连接FC,如图所示:
∵D、E分别是AB、AC的中点,
∴AD=BD,AE=CE,
在△ADE与△CFE中,
,
∴△ADE≌△CFE(SAS),
∴∠ADE=∠F,AD=CF,
∴CF∥AB,CF=BD,
∴四边形BCFD是平行四边形,
∴DF=BC,DF∥BC,
∴DE=DF=BC.
20.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∴∠BAE=∠DCF,
在△ABE与△CDF中,
,
∴△ABE≌△CDF(SAS),
∴∠AEB=∠CFD,
∴∠BEF=∠DFE,
∴BE∥DF;
(2)解:由(1)知,△ABE≌△CDF,BE∥DF,
∴BE=DF,
∴四边形BEDF是平行四边形,
∴DO=BO,
∵OM⊥BD,
∴DM=BM,
∵△BFM的周长为12,
∴BM+MF+BF=DM+MF+BF=DF+BF=12,
∴四边形BEDF的周长为24.
21.解:(1)∵点A(1,2),点B(2,0),
∴AB==,
设直线AB的解析式为y=kx+b,
,
解得:,
∴直线AB的解析式为y=﹣2x+4;
(2)设点C(x,y),
当OA,OB为边时,∵四边形OACB是平行四边形,
∴AB与OC互相平分,
∴,=,
∴x=3,y=2,
∴点C(3,2);
当OB、AB为边时,∵四边形ABOC是平行四边形,
∴OA与BC互相平分,
∴,
∴x=﹣1,y=2,
∴点C(﹣1,2);
当AO、AB为边时,∵四边形OABC是平行四边形,
∴AC与OB互相平分,
∴,,
∴x=1,y=﹣2,
∴点C(1,﹣2),
综上所述:点C坐标为:(3,2)或(﹣1,2)或(1,﹣2).
22.证明:∵AE⊥BD,CF⊥BD,
∴∠AED=∠AEF=∠CFB=∠CFE=90°,
∵四边形ABCD是平行四边形,
∴AD=CB,AD∥CB,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(AAS),
∴AE=CF,
又∵∠AEF=∠CFE,
∴AE∥CF,
∴四边形AFCE是平行四边形
一.选择题(共12小题)
1.如图,在四边形ABCD中,对角线AC、BD相交于点O.下列条件不能判定四边形ABCD为平行四边形的是( )
A.AB∥CD,AD∥BC B.OA=OC,OB=OD
C.AB=CD,AD=BC D.AB∥CD,AD=BC
2.如图,a∥b,点A在直线a上,点B、C在直线b上,AC⊥b,如果AB=5cm,AC=4cm,那么平行线a、b之间的距离为( )
A.5cm B.4cm C.3cm D.不能确定
3.如图,在△ABC中,AB=8,∠C=90°,∠A=30°,DE是中位线,则DE的长为( )
A.2 B.3 C.4 D.2
4.如图所示,已知直线a∥b,点A,C,F在直线a上,点B,D,E,G在直线b上,且AB∥CD,CE⊥b,FG⊥b,则下列说法中不正确的有( )
①AB=FG;②A,B两点的距离就是线段AB的长,③EC=FG;④直线a,b的距离就是线段CD的长.
A.1个 B.2个 C.3个 D.4个
5.如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE=6,则AC的长为( )
A.3 B. C.9 D.
6.如图,平行四边形ABCD中,O为对角线交点,DP平分∠ADC,CP平分∠BCD,AB=7,AD=10,则OP的长为( )
A.1.5 B.2 C.2.5 D.3
7.如图,在平面直角坐标系中, OABC的顶点O、A、C的坐标分别是(0,0),(3,0),(1,2),则点B的坐标是( )
A.(2,4) B.(4,2) C.(5,3) D.(4,3)
8.在平面直角坐标系中,有A(﹣1,2),B(3,1),C(1,4)三点,另有一点D与点A,B,C构成平行四边形,则点D的坐标不可能是( )
A.(﹣3,5) B.(1,﹣1) C.(5,3) D.(4,2)
9.如图1,直线l1∥l2,直线l3分别交直线l1,l2于点A,B.小嘉在图1的基础上进行尺规作图,得到如图2,并探究得到下面两个结论:
①四边形ABCD是邻边不相等的平行四边形;
②四边形ABCD是对角线互相垂直的平行四边形.下列判断正确的是( )
A.①②都正确 B.①错误,②正确
C.①②都错误 D.①正确,②错误
10.如图,O是 ABCD对角线AC上一点,过O作EF∥AD交AB于点E,交CD于点F,GH∥AB交AD于点G,交BC于点H,连结GE,GF,HE,HF,若已知下列图形的面积,不能求出 ABCD面积的是( )
A.四边形EHFG
B.△AEG和△CHF
C.四边形EBHO和四边形GOFD
D.△AEO和四边形GOFD
11.如图,在平行四边形ABCD中,分别以AB、AD为边向外作等边△ABE和等边△ADF,延长CB交AE于点G,点G在点A、E之间,连接CE、CF、EF,则以下四个结论,正确的是( )
①△CDF≌△EBC;②∠CDF=∠EAF;③CG⊥AE;④△CEF是等边三角形.
A.③④ B.①②④ C.①②③ D.①②③④
12.如图,在平行四边形ABCD中,点F是BC上一点,BF=6,CF=2,点E是CD的中点,AE平分∠DAF,EF=,则△AEF的面积是( )
A. B. C. D.
二.填空题(共5小题)
13.如图,已知AD∥BC,CE=5,CF=8,且CE⊥AD,CF⊥AB垂足分别为E,F.则AD与BC间的距离是 .
14.如图,在△ABC中,点D、E分别是AB、AC的中点,点F在DE上,且AF⊥CF,若AC=3,BC=6,则DF的长为 .
15.如图,在四边形ABCD中,AD∥BC,BC=6厘米,AD=9厘米,P、Q分别从A、C同时出发,P以1厘米/秒的速度由A向D运动,Q以2厘米/秒的速度由C向B运动.设运动的时间为t秒,则当t= 时,直线PQ将四边形ABCD截出一个平行四边形.
16.如图,在 ABCD中,点F在边AD上,AF=2FD,直线BF与对角线AC相交于点E,交CD的延长线于点G,如果BE=2,那么EG的长是 .
17.如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了一个四边形.在转动其中一张纸条的过程中,线段AD和BC的长度始终相等,这里蕴含的数学原理是 .
三.解答题(共5小题)
18.如图,直线a∥b,AB与a,b分别相交于点A,B,且AC⊥AB,AC交直线b于点C.
(1)若∠1=58°,求∠2的度数;
(2)若AC=5,AB=12,BC=13,求直线a与b的距离.
19.求证:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
已知:如图,点D、E分别是△ABC的边AB、AC的中点,连接DE.
求证:DE∥BC,且DE=BC.
(要求:尺规作图画出D点和E点,只保留作图痕迹,不写作法)
20.如图, ABCD的对角线AC,BD相交于点O,点E,F在AC上,且AE=CF.
(1)求证:BE∥DF;
(2)过点O作OM⊥BD,垂足为O,交DF于点M,若△BFM的周长为12,求四边形BEDF的周长.
21.如图,点A(1,2),点B(2,0).求:
(1)求OA和AB的解析式;
(2)在坐标平面内存在一点C,使得以O、A、C、B为顶点的四边形为平行四边形,直接写出点C的坐标.
22.如图,在 ABCD中,分别过A,C两点作对角线BD的垂线,垂足分别为E,F.
求证:四边形AFCE是平行四边形.
参考答案
一.选择题(共12小题)
1--10DBABD ABDBC 11--12BD
二.填空题(共5小题)
13.5
14.1.5
15.2或3
16.3
故答案为:3.
17.平行四边形的对边相等.
三.解答题(共5小题)
18.解:(1)∵AC⊥AB,
∴∠BAC=90°,
∵∠1=58°,
∴∠ABC=90°﹣58°=32°,
∵a∥b,
∴∠2=∠ABC=32°;
(2)如图,过点A作AD⊥BC,垂足为D,
所以线段AD的长度等于a与b之间的距离,
因为AB⊥AC
所以AB AC=BC AD,
所以AD=,
所以a与b的距离为.
19.证明:分别作线段AB和线段AC的垂直平分线,交点分别为点D和E,延长DE到F,使EF=DE,连接FC,如图所示:
∵D、E分别是AB、AC的中点,
∴AD=BD,AE=CE,
在△ADE与△CFE中,
,
∴△ADE≌△CFE(SAS),
∴∠ADE=∠F,AD=CF,
∴CF∥AB,CF=BD,
∴四边形BCFD是平行四边形,
∴DF=BC,DF∥BC,
∴DE=DF=BC.
20.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∴∠BAE=∠DCF,
在△ABE与△CDF中,
,
∴△ABE≌△CDF(SAS),
∴∠AEB=∠CFD,
∴∠BEF=∠DFE,
∴BE∥DF;
(2)解:由(1)知,△ABE≌△CDF,BE∥DF,
∴BE=DF,
∴四边形BEDF是平行四边形,
∴DO=BO,
∵OM⊥BD,
∴DM=BM,
∵△BFM的周长为12,
∴BM+MF+BF=DM+MF+BF=DF+BF=12,
∴四边形BEDF的周长为24.
21.解:(1)∵点A(1,2),点B(2,0),
∴AB==,
设直线AB的解析式为y=kx+b,
,
解得:,
∴直线AB的解析式为y=﹣2x+4;
(2)设点C(x,y),
当OA,OB为边时,∵四边形OACB是平行四边形,
∴AB与OC互相平分,
∴,=,
∴x=3,y=2,
∴点C(3,2);
当OB、AB为边时,∵四边形ABOC是平行四边形,
∴OA与BC互相平分,
∴,
∴x=﹣1,y=2,
∴点C(﹣1,2);
当AO、AB为边时,∵四边形OABC是平行四边形,
∴AC与OB互相平分,
∴,,
∴x=1,y=﹣2,
∴点C(1,﹣2),
综上所述:点C坐标为:(3,2)或(﹣1,2)或(1,﹣2).
22.证明:∵AE⊥BD,CF⊥BD,
∴∠AED=∠AEF=∠CFB=∠CFE=90°,
∵四边形ABCD是平行四边形,
∴AD=CB,AD∥CB,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(AAS),
∴AE=CF,
又∵∠AEF=∠CFE,
∴AE∥CF,
∴四边形AFCE是平行四边形
