第五章 基本平面图形 综合测试卷(含答案)
文档属性
| 名称 | 第五章 基本平面图形 综合测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-27 15:57:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第五章 基本平面图形
综合测试卷
时间: 60分钟 满分: 120分 得分:____________
一、选择题(每题 3 分,共 36 分)
1.下列说法正确的是 ( )
A.角的度量中, B. 射线 AB 的长度为 3cm
C.经过两点可以画并且只能画一条直线 D.延长直线 AB
2.如图,下列说法中不正确的是 ( )
A.直线 AB与直线 BA 是同一条直线 B.射线OA 与射线AB 是同一条射线
C.线段 AB与线段 BA 是同一条线段 D.射线 OA 与射线OB 是同一条射线
第 2 题图 第 3 题图
3.如图,∠α的另一种正确的表示方法是 ( )
A.∠1 B.∠C C.∠ACB D.∠ABC
4.下列判断正确的是 ( )
A.平角是一条直线 B. 凡是直角都相等
C.两个锐角的和一定是锐角 D.角的大小与两条边的长短有关
5.在研究多边形的几何性质时,我们常常把它分割成三角形进行研究.从八边形的一个顶点引对角线,最多把它分割成三角形的个数为 ( )
A.4 B.5 C.6 D.7
6.生活中,有下列两个现象,对于这两个现象的解释,正确的是 ( )
A.均用两点之间线段最短来解释
B.均用经过两点有且只有一条直线来解释
C.现象1用两点之间线段最短来解释,现象2 用经过两点有且只有一条直线来解释
D.现象1用经过两点有且只有一条直线来解释,现象2 用两点之间线段最短来解释
7.在灯塔O 处观测到轮船 A 位于北偏西54°的方向,同时轮船 B 在南偏东 15°的方向,那么∠AOB 的大小为 ( )
A.69° B. 111° C. 141° D. 159°
8.每天中午12 点 30分“校园之声”节目都会如约而至,此时时针与分针所夹的角为 ( )
A.180° B.165° C.155° D.150°
9.把 40°12′36"化为用度表示,下列正确的是 ( )
A.40.11° B.40.21° C.40.16° D.40.26°
10.如图, 且AF=CD,则 DF为AB 长的( )
11.如图,已知∠AOB=130°,以点 O为顶点作直角∠COB,以点O为端点作一条射线OD.通过折叠的方法,使OD与OC重合,点B落在点B'处,OE 所在的直线为折痕,若∠COE=15°,则 ( )
A.30° B.25° C.20° D.15°
12.如图,将两块直角三角尺的直角顶点 O 叠放在一起,若∠AOD=130°,则∠BOC 的度数为 ( )
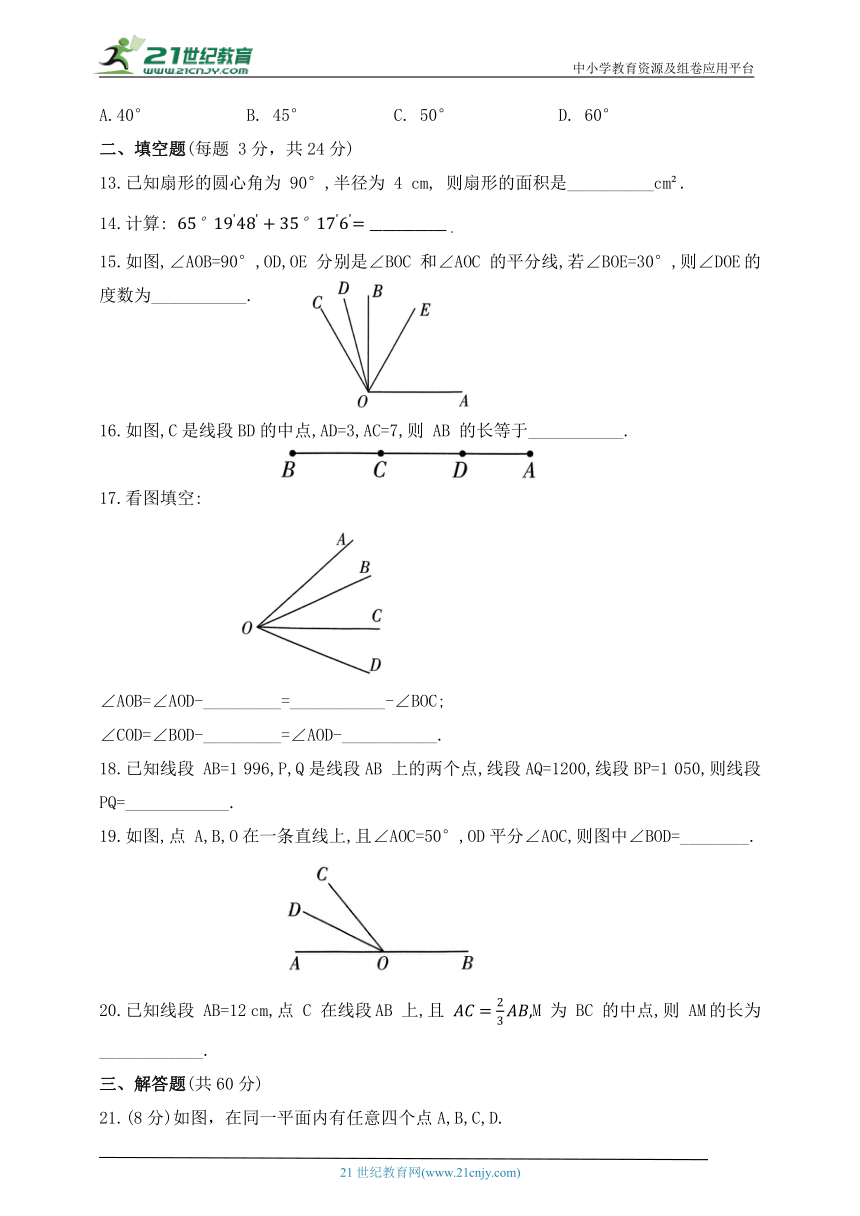
A.40° B. 45° C. 50° D. 60°
二、填空题(每题 3分,共24分)
13.已知扇形的圆心角为 90°,半径为 4 cm, 则扇形的面积是__________cm .
14.计算:
15.如图,∠AOB=90°,OD,OE 分别是∠BOC 和∠AOC 的平分线,若∠BOE=30°,则∠DOE的度数为___________.
16.如图,C是线段BD的中点,AD=3,AC=7,则 AB 的长等于___________.
17.看图填空:
∠AOB=∠AOD-_________=___________-∠BOC;
∠COD=∠BOD-_________=∠AOD-___________.
18.已知线段 AB=1 996,P,Q是线段AB 上的两个点,线段AQ=1200,线段BP=1 050,则线段 PQ=____________.
19.如图,点 A,B,O在一条直线上,且∠AOC=50°,OD平分∠AOC,则图中∠BOD=________.
20.已知线段 AB=12 cm,点 C 在线段AB 上,且 M 为 BC 的中点,则 AM的长为____________.
三、解答题(共60分)
21.(8分)如图,在同一平面内有任意四个点A,B,C,D.
(1)按要求补充图形:画出直线 AB,射线 BC,BD,连接 DC;
(2)若小明在(1)的基础上测量∠ABD=61°42′15",∠CBD=15°30',求∠ABC的度数;
(3)若(1)(2)基础上,小亮又测量∠BDC=15.5°,比较∠BDC与∠CBD的大小.
22.(8分)已知OC是∠AOB内部的一条射线,∠AOC=30°,OE是∠COB的平分线.当 ∠COE=40°时,求∠AOB的度数.
解:因为 OE是的平分线,
所以 (理由:________________________).
因为 所以____________,
因为 所以
23.(8分)如图,点C是AB的中点,D,E分别是线段AC,CB上的点,且若求线段CE的长.
24.(12分)如图所示, 已知点 C,D是线段AB上的两个点,点M,N分别为AC,BD的中点.
(1)若 求 的长及点 M,N之间的距离.
(2)如果 ,用含 a,b的式子表示 MN 的长.
25.(12分)如图,点 O 为直线 AB 上一点, ∠COD=90°,OE平分∠AOC,OF 平分∠BOD.
(1)若∠AOE=10°,求∠BOD的度数;
(2)若∠AOC:∠COB=2:13,求∠BOF 的度数.
26.(12分)如图,已知∠AOB=90°,三角形COD 是含有45°角的三角板,∠COD=45°,OE平分∠BOC.
(1)如图1,当∠AOC=30°时,∠DOE=____________°;
(2)如图2,当∠AOC=60°时,∠DOE=____________°;
(3)如图3,当∠AOC=α(90°<α<180°)时,求∠DOE 的度数(用α表示);
(4)由前三步的计算,当0°<∠AOC<180°时,请直接写出∠AOC与∠DOE的数量关系为____________.
参考答案
1. C 2. B 3. C 4. B 5. C 6. D 7. C 8. B
9. B 10. C 11. C 12. C
13.4π 14.100°36′54" 15.45° 16.11
17.∠BOD ∠AOC ∠BOC ∠AOC
18.254 19.155° 20.10 cm
21.解:(1)直线 AB,射线 BC,BD,线段 DC,如图所示:
(2) 因为 ∠ABD= 61°42′15",∠CBD =15°30',
∠ABC=∠ABD+∠CBD=61°42'15"+
(3)因为∠CBD=15°30'=15.5°,
又因为∠BDC=15.5°,所以∠CBD=∠BDC.
22.解:因为 OE 是∠COB的平分线,所以∠COB=2∠COE(理由:角平分线的定义).
因为∠COE=40°,所以∠COB=80°,
因为∠AOC=30°,所以∠AOB=∠AOC+BOC=110°.
故答案为:2∠COE,角平分线定义,∠COB=80°,30°,∠BOC.
23.解:因为点C 是线段 AB 的中点,所以
因为 所以
又因为
所以
24.(1)解:因为 AB=10 cm,CD=4 cm,所以 AC+BD=AB-CD=10-4=6(cm),
因为点 M,N分别为AC,BD的中点,所以 BD)=3(cm),
所以 MN=AB-(AM+BN)=10-3=7(cm);
(2)根据(1)的结论,
所以
25.解:(1) 因为 OE 平分∠AOC,OF 平分∠BOD,
所以∠AOC=2∠AOE=20°,所以∠BOD=180°-∠AOC-∠COD=70°,
所以∠BOD的度数为 70°;
(2)因为∠AOC:∠COB=2:13,∠AOC+∠COB=180°,
所以 所以∠BOD=180°-∠AOC-∠COD=66°,
因为 OF平分∠BOD,所以 所以∠BOF的度数为33°.
26.解:(1)因为∠AOB=90°,∠AOC=30°,所以∠BOC=∠AOB-∠AOC=60°,
因为OE平分∠BOC,所以
因为∠COD=45°,所以∠DOE=∠COD-∠EOC=15°,
故答案为:15;
(2)因为∠AOB=90°,∠AOC=60°,所以∠BOC=∠AOB-∠AOC=30°,
因为OE平分∠BOC,所以
因为∠COD=45°,所以∠DOE=∠COD-∠EOC=30°,
故答案为:30;
(3)因为∠AOB=90°,∠AOC=α(90°<α<180°),所以∠BOC=∠AOC-∠AOB=α-90°,
因为 OE平分∠BOC,所以
因为∠COD=45°,所以
(4)设∠AOC=x(0°<x<180°),
①如图1和图2,当0°<x≤90°时,
因为∠AOB=90°,∠AOC=x,所以∠BOC=∠AOB-∠AOC=90°-x,
因为 OE 平分∠BOC,所以
因为∠COD=45°,所以 即∠AOC=2∠DOE;
②如图3,当90°<x<180°时,
同(3)可得 则∠AOC=2∠DOE.
综上所述,∠AOC与∠DOE 的数量关系为∠AOC=2∠DOE.
故答案为:∠AOC=2∠DOE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 基本平面图形
综合测试卷
时间: 60分钟 满分: 120分 得分:____________
一、选择题(每题 3 分,共 36 分)
1.下列说法正确的是 ( )
A.角的度量中, B. 射线 AB 的长度为 3cm
C.经过两点可以画并且只能画一条直线 D.延长直线 AB
2.如图,下列说法中不正确的是 ( )
A.直线 AB与直线 BA 是同一条直线 B.射线OA 与射线AB 是同一条射线
C.线段 AB与线段 BA 是同一条线段 D.射线 OA 与射线OB 是同一条射线
第 2 题图 第 3 题图
3.如图,∠α的另一种正确的表示方法是 ( )
A.∠1 B.∠C C.∠ACB D.∠ABC
4.下列判断正确的是 ( )
A.平角是一条直线 B. 凡是直角都相等
C.两个锐角的和一定是锐角 D.角的大小与两条边的长短有关
5.在研究多边形的几何性质时,我们常常把它分割成三角形进行研究.从八边形的一个顶点引对角线,最多把它分割成三角形的个数为 ( )
A.4 B.5 C.6 D.7
6.生活中,有下列两个现象,对于这两个现象的解释,正确的是 ( )
A.均用两点之间线段最短来解释
B.均用经过两点有且只有一条直线来解释
C.现象1用两点之间线段最短来解释,现象2 用经过两点有且只有一条直线来解释
D.现象1用经过两点有且只有一条直线来解释,现象2 用两点之间线段最短来解释
7.在灯塔O 处观测到轮船 A 位于北偏西54°的方向,同时轮船 B 在南偏东 15°的方向,那么∠AOB 的大小为 ( )
A.69° B. 111° C. 141° D. 159°
8.每天中午12 点 30分“校园之声”节目都会如约而至,此时时针与分针所夹的角为 ( )
A.180° B.165° C.155° D.150°
9.把 40°12′36"化为用度表示,下列正确的是 ( )
A.40.11° B.40.21° C.40.16° D.40.26°
10.如图, 且AF=CD,则 DF为AB 长的( )
11.如图,已知∠AOB=130°,以点 O为顶点作直角∠COB,以点O为端点作一条射线OD.通过折叠的方法,使OD与OC重合,点B落在点B'处,OE 所在的直线为折痕,若∠COE=15°,则 ( )
A.30° B.25° C.20° D.15°
12.如图,将两块直角三角尺的直角顶点 O 叠放在一起,若∠AOD=130°,则∠BOC 的度数为 ( )
A.40° B. 45° C. 50° D. 60°
二、填空题(每题 3分,共24分)
13.已知扇形的圆心角为 90°,半径为 4 cm, 则扇形的面积是__________cm .
14.计算:
15.如图,∠AOB=90°,OD,OE 分别是∠BOC 和∠AOC 的平分线,若∠BOE=30°,则∠DOE的度数为___________.
16.如图,C是线段BD的中点,AD=3,AC=7,则 AB 的长等于___________.
17.看图填空:
∠AOB=∠AOD-_________=___________-∠BOC;
∠COD=∠BOD-_________=∠AOD-___________.
18.已知线段 AB=1 996,P,Q是线段AB 上的两个点,线段AQ=1200,线段BP=1 050,则线段 PQ=____________.
19.如图,点 A,B,O在一条直线上,且∠AOC=50°,OD平分∠AOC,则图中∠BOD=________.
20.已知线段 AB=12 cm,点 C 在线段AB 上,且 M 为 BC 的中点,则 AM的长为____________.
三、解答题(共60分)
21.(8分)如图,在同一平面内有任意四个点A,B,C,D.
(1)按要求补充图形:画出直线 AB,射线 BC,BD,连接 DC;
(2)若小明在(1)的基础上测量∠ABD=61°42′15",∠CBD=15°30',求∠ABC的度数;
(3)若(1)(2)基础上,小亮又测量∠BDC=15.5°,比较∠BDC与∠CBD的大小.
22.(8分)已知OC是∠AOB内部的一条射线,∠AOC=30°,OE是∠COB的平分线.当 ∠COE=40°时,求∠AOB的度数.
解:因为 OE是的平分线,
所以 (理由:________________________).
因为 所以____________,
因为 所以
23.(8分)如图,点C是AB的中点,D,E分别是线段AC,CB上的点,且若求线段CE的长.
24.(12分)如图所示, 已知点 C,D是线段AB上的两个点,点M,N分别为AC,BD的中点.
(1)若 求 的长及点 M,N之间的距离.
(2)如果 ,用含 a,b的式子表示 MN 的长.
25.(12分)如图,点 O 为直线 AB 上一点, ∠COD=90°,OE平分∠AOC,OF 平分∠BOD.
(1)若∠AOE=10°,求∠BOD的度数;
(2)若∠AOC:∠COB=2:13,求∠BOF 的度数.
26.(12分)如图,已知∠AOB=90°,三角形COD 是含有45°角的三角板,∠COD=45°,OE平分∠BOC.
(1)如图1,当∠AOC=30°时,∠DOE=____________°;
(2)如图2,当∠AOC=60°时,∠DOE=____________°;
(3)如图3,当∠AOC=α(90°<α<180°)时,求∠DOE 的度数(用α表示);
(4)由前三步的计算,当0°<∠AOC<180°时,请直接写出∠AOC与∠DOE的数量关系为____________.
参考答案
1. C 2. B 3. C 4. B 5. C 6. D 7. C 8. B
9. B 10. C 11. C 12. C
13.4π 14.100°36′54" 15.45° 16.11
17.∠BOD ∠AOC ∠BOC ∠AOC
18.254 19.155° 20.10 cm
21.解:(1)直线 AB,射线 BC,BD,线段 DC,如图所示:
(2) 因为 ∠ABD= 61°42′15",∠CBD =15°30',
∠ABC=∠ABD+∠CBD=61°42'15"+
(3)因为∠CBD=15°30'=15.5°,
又因为∠BDC=15.5°,所以∠CBD=∠BDC.
22.解:因为 OE 是∠COB的平分线,所以∠COB=2∠COE(理由:角平分线的定义).
因为∠COE=40°,所以∠COB=80°,
因为∠AOC=30°,所以∠AOB=∠AOC+BOC=110°.
故答案为:2∠COE,角平分线定义,∠COB=80°,30°,∠BOC.
23.解:因为点C 是线段 AB 的中点,所以
因为 所以
又因为
所以
24.(1)解:因为 AB=10 cm,CD=4 cm,所以 AC+BD=AB-CD=10-4=6(cm),
因为点 M,N分别为AC,BD的中点,所以 BD)=3(cm),
所以 MN=AB-(AM+BN)=10-3=7(cm);
(2)根据(1)的结论,
所以
25.解:(1) 因为 OE 平分∠AOC,OF 平分∠BOD,
所以∠AOC=2∠AOE=20°,所以∠BOD=180°-∠AOC-∠COD=70°,
所以∠BOD的度数为 70°;
(2)因为∠AOC:∠COB=2:13,∠AOC+∠COB=180°,
所以 所以∠BOD=180°-∠AOC-∠COD=66°,
因为 OF平分∠BOD,所以 所以∠BOF的度数为33°.
26.解:(1)因为∠AOB=90°,∠AOC=30°,所以∠BOC=∠AOB-∠AOC=60°,
因为OE平分∠BOC,所以
因为∠COD=45°,所以∠DOE=∠COD-∠EOC=15°,
故答案为:15;
(2)因为∠AOB=90°,∠AOC=60°,所以∠BOC=∠AOB-∠AOC=30°,
因为OE平分∠BOC,所以
因为∠COD=45°,所以∠DOE=∠COD-∠EOC=30°,
故答案为:30;
(3)因为∠AOB=90°,∠AOC=α(90°<α<180°),所以∠BOC=∠AOC-∠AOB=α-90°,
因为 OE平分∠BOC,所以
因为∠COD=45°,所以
(4)设∠AOC=x(0°<x<180°),
①如图1和图2,当0°<x≤90°时,
因为∠AOB=90°,∠AOC=x,所以∠BOC=∠AOB-∠AOC=90°-x,
因为 OE 平分∠BOC,所以
因为∠COD=45°,所以 即∠AOC=2∠DOE;
②如图3,当90°<x<180°时,
同(3)可得 则∠AOC=2∠DOE.
综上所述,∠AOC与∠DOE 的数量关系为∠AOC=2∠DOE.
故答案为:∠AOC=2∠DOE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
