4.3.2 利用完全平方公式分解因式 课件(共20张PPT)
文档属性
| 名称 | 4.3.2 利用完全平方公式分解因式 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 432.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:36:00 | ||
图片预览








文档简介
(共20张PPT)
第4章 因式分解
4.3 公式法
第2课时 利用完全平方公式因式分解
1.通过利用完全平方公式分解因式,发展学生的逆向思维和推理能力
2.培养学生灵活运用知识的能力和积极思考的良好行为
1.掌握公式法中的完全平方公式进行分解因式.
2.灵活地运用公式法或已学过的提公因式法进行分解因式,正确判断因式分解的彻底性问题.
教学目标
重难点
复习导入
1.把下列各式因式分解:
(1)4a2-9b2; (2)ax4-ax2.
2.你能用前面学过的方法把多项式x2+8x+16因式分解吗,这个多项式有什么特点?
解:(1)原式=(2a+3b)(2a-3b);
(2)原式=ax2(x+1)(x-1).
探究新知
3.填空:
(1)(x+2)2=_______________;
(2)(2x-y)2=________________;
反过来:(1)_______________=(x+2)2;
(2)________________=(2x-y)2.
x2+4x+4
4x2-4xy+y2
x2+4x+4
4x2-4xy+y2
以上运算,哪些是整式乘法,哪些是因式分解?你能说明整式乘法与因式分解的关系吗?
归纳旧知
完全平方式的特点:
1. 必须是三项式 (或可以看成三项的);
2. 有两个数或式的平方和;
3. 有两底数之积的 ±2 倍.
完全平方式:
简记口诀:
首平方,尾平方,首尾两倍在中央.
归纳新知
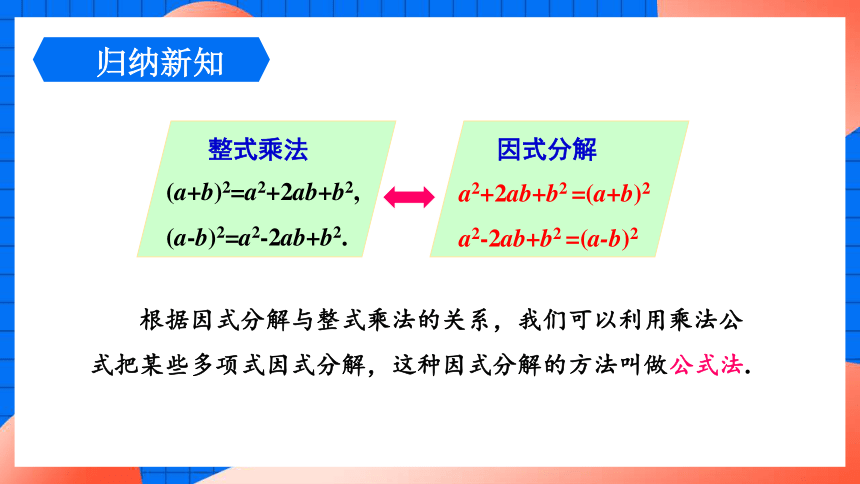
根据因式分解与整式乘法的关系,我们可以利用乘法公式把某些多项式因式分解,这种因式分解的方法叫做公式法.
(a+b)2=a2+2ab+b2,
(a-b)2=a2-2ab+b2.
整式乘法
因式分解
a2+2ab+b2 =(a+b)2
a2-2ab+b2 =(a-b)2
小牛试刀
下列多项式是不是完全平方式?
(1)a2 - 4a + 4
(2)x2 + 4x + 4y2
(3)4a2 + 2ab + b2
1
4
(4)a2 - ab + b2
(5)x2 - 6x - 9
(6)a2 + a+ 0.25
是
不是
是
不是
不是
是
典型例题
【例1】把下列完全平方式因式分解:
(1)x2+14x+49;
【分析】在(1)中49=72,14x=2·x·7,所以x2+14x+49是一个完全平方式,即:
x2+14x+49=x2 + 2 × x × 7 + 72= (x + 7)2
头2+2·头·尾+尾2=(头+尾)2
解:原式=(x+7)2;
典型例题
【例1】把下列完全平方式因式分解:
(2)(m+n)2-6(m+n)+9.
【分析】在(2)中多项式中的两个平方项分别是(m+n)2和32,另一项6(m+n)=2·(m+n)·3,符合完全平方式的形式,这里“m+n”相当于完全平方式中的a,“3”相当于完全平方式中的b,如果将(m+n)看作一个整体,即:
(m+n)2-6(m+n)+9=(m+n)2-2×(m+n)×3+32=[(m+n) - 3]2
头2 - 2 · 头 · 尾 +尾2 = (头 - 尾)2
解:原式=[(m+n)-3]2=(m+n-3)2.
典型例题
例2 分解因式:
(1) 16x2 + 24x + 9; (2) -x2 + 4xy - 4y2.
分析:(1)中 16x2 = (4x)2,9 = 3 ;24x = 2×4x·3;所以16x2+24x+9 是一个完全平方式,即 16x2 + 24x + 9 = (4x)2 + 2×4x·3 + (3)2.
+2
a
b
+ b2
a2
(2)中首项有负号,一般先利用添括号法则,将其变形为 - (x2 - 4xy
+ 4y2 ),然后再利用公式分解因式.
典型例题
解:(1) 16x2 + 24x + 9
= (4x + 3)2.
= (4x)2 + 2·4x·3 + (3)2
(2) -x2 + 4xy - 4y2
= -(x2 - 4xy + 4y2)
= -(x - 2y)2.
典型例题
例3. 因式分解:
(1) -3a2x2+24a2x - 48a2;
(2) (a2+4)2 - 16a2.
=(a2+4+4a)(a2+4 - 4a)
解:(1) 原式=-3a2(x2 - 8x+16)
=-3a2(x - 4)2.
(2) 原式=(a2+4)2 - (4a)2
=(a+2)2(a - 2)2.
有公因式要先提公因式
要检查每一个多项式的因式,看能否继续分解
归纳总结
因式分解的一般步骤:
(1)如果多项式的各项含有公因式,那么应先提取公因式;
(2)如果多项式的各项不含有公因式,那么可以尝试运用公式法因式分解;
(3)因式分解必须分解到每一个因式都不能再分解为止.
随堂练习
1.若a+b=2,则a2+2ab+b2的值是( )
A.8 B.16 C.2 D.4
2.如果x2+6x+k是一个完全平方式,那么k的值是______.
9
D
随堂练习
3. 下列四个多项式中,能因式分解的是 ( )
A.a2+1 B.a2-6a+9
C.x2+5y D.x2-5y
4. 把多项式 4x2y-4xy2-x3 分解因式的结果是 ( )
A.4xy(x-y)-x3 B.-x(x-2y)2
C.x(4xy-4y2-x2) D.-x(-4xy+4y2+x2)
B
B
5. 若关于 x 的多项式 x2-8x+m2 是完全平方式,则 m 的值为______.
±4
随堂练习
6.分解因式:
(1) x2 + 12x + 36; (2) - 2xy - x2 - y2;
(3) a2 + 2a + 1; (4) 4x2 - 4x + 1;
(5) ax2 + 2a2x + a3; (6) - 3x2 + 6xy - 3y2.
解:(1)(x + 6)2;(2)- (x + y)2;
(3)(a + 1)2;(4)(2x - 1)2;
(5)a(x + a)2;(6)- 3(x - y)2.
随堂练习
7. (1) 已知 a-b=3,求 a(a-2b)+b2 的值;
(2) 已知 ab=2,a+b=5,求 a3b+2a2b2+ab3 的值.
原式=2×52 = 50.
解:(1) 原式=a2-2ab+b2=(a-b)2.
当 a-b=3 时,原式=32=9.
(2) 原式=ab(a2+2ab+b2)=ab(a+b)2.
当 ab=2,a+b=5 时,
课堂小结
完全平方公式分解因式
公式
a2±2ab+b2=(a±b)2
特点
(1)要求多项式有三项.
(2)其中两项同号,且都可以写成某数或式的平方,另一项则是这两数或式的乘积的2倍,符号可正可负.
课后作业
完成教材习题4.5
这节课你学到了什么?谈谈你的收获,
小结与反思
第4章 因式分解
4.3 公式法
第2课时 利用完全平方公式因式分解
1.通过利用完全平方公式分解因式,发展学生的逆向思维和推理能力
2.培养学生灵活运用知识的能力和积极思考的良好行为
1.掌握公式法中的完全平方公式进行分解因式.
2.灵活地运用公式法或已学过的提公因式法进行分解因式,正确判断因式分解的彻底性问题.
教学目标
重难点
复习导入
1.把下列各式因式分解:
(1)4a2-9b2; (2)ax4-ax2.
2.你能用前面学过的方法把多项式x2+8x+16因式分解吗,这个多项式有什么特点?
解:(1)原式=(2a+3b)(2a-3b);
(2)原式=ax2(x+1)(x-1).
探究新知
3.填空:
(1)(x+2)2=_______________;
(2)(2x-y)2=________________;
反过来:(1)_______________=(x+2)2;
(2)________________=(2x-y)2.
x2+4x+4
4x2-4xy+y2
x2+4x+4
4x2-4xy+y2
以上运算,哪些是整式乘法,哪些是因式分解?你能说明整式乘法与因式分解的关系吗?
归纳旧知
完全平方式的特点:
1. 必须是三项式 (或可以看成三项的);
2. 有两个数或式的平方和;
3. 有两底数之积的 ±2 倍.
完全平方式:
简记口诀:
首平方,尾平方,首尾两倍在中央.
归纳新知
根据因式分解与整式乘法的关系,我们可以利用乘法公式把某些多项式因式分解,这种因式分解的方法叫做公式法.
(a+b)2=a2+2ab+b2,
(a-b)2=a2-2ab+b2.
整式乘法
因式分解
a2+2ab+b2 =(a+b)2
a2-2ab+b2 =(a-b)2
小牛试刀
下列多项式是不是完全平方式?
(1)a2 - 4a + 4
(2)x2 + 4x + 4y2
(3)4a2 + 2ab + b2
1
4
(4)a2 - ab + b2
(5)x2 - 6x - 9
(6)a2 + a+ 0.25
是
不是
是
不是
不是
是
典型例题
【例1】把下列完全平方式因式分解:
(1)x2+14x+49;
【分析】在(1)中49=72,14x=2·x·7,所以x2+14x+49是一个完全平方式,即:
x2+14x+49=x2 + 2 × x × 7 + 72= (x + 7)2
头2+2·头·尾+尾2=(头+尾)2
解:原式=(x+7)2;
典型例题
【例1】把下列完全平方式因式分解:
(2)(m+n)2-6(m+n)+9.
【分析】在(2)中多项式中的两个平方项分别是(m+n)2和32,另一项6(m+n)=2·(m+n)·3,符合完全平方式的形式,这里“m+n”相当于完全平方式中的a,“3”相当于完全平方式中的b,如果将(m+n)看作一个整体,即:
(m+n)2-6(m+n)+9=(m+n)2-2×(m+n)×3+32=[(m+n) - 3]2
头2 - 2 · 头 · 尾 +尾2 = (头 - 尾)2
解:原式=[(m+n)-3]2=(m+n-3)2.
典型例题
例2 分解因式:
(1) 16x2 + 24x + 9; (2) -x2 + 4xy - 4y2.
分析:(1)中 16x2 = (4x)2,9 = 3 ;24x = 2×4x·3;所以16x2+24x+9 是一个完全平方式,即 16x2 + 24x + 9 = (4x)2 + 2×4x·3 + (3)2.
+2
a
b
+ b2
a2
(2)中首项有负号,一般先利用添括号法则,将其变形为 - (x2 - 4xy
+ 4y2 ),然后再利用公式分解因式.
典型例题
解:(1) 16x2 + 24x + 9
= (4x + 3)2.
= (4x)2 + 2·4x·3 + (3)2
(2) -x2 + 4xy - 4y2
= -(x2 - 4xy + 4y2)
= -(x - 2y)2.
典型例题
例3. 因式分解:
(1) -3a2x2+24a2x - 48a2;
(2) (a2+4)2 - 16a2.
=(a2+4+4a)(a2+4 - 4a)
解:(1) 原式=-3a2(x2 - 8x+16)
=-3a2(x - 4)2.
(2) 原式=(a2+4)2 - (4a)2
=(a+2)2(a - 2)2.
有公因式要先提公因式
要检查每一个多项式的因式,看能否继续分解
归纳总结
因式分解的一般步骤:
(1)如果多项式的各项含有公因式,那么应先提取公因式;
(2)如果多项式的各项不含有公因式,那么可以尝试运用公式法因式分解;
(3)因式分解必须分解到每一个因式都不能再分解为止.
随堂练习
1.若a+b=2,则a2+2ab+b2的值是( )
A.8 B.16 C.2 D.4
2.如果x2+6x+k是一个完全平方式,那么k的值是______.
9
D
随堂练习
3. 下列四个多项式中,能因式分解的是 ( )
A.a2+1 B.a2-6a+9
C.x2+5y D.x2-5y
4. 把多项式 4x2y-4xy2-x3 分解因式的结果是 ( )
A.4xy(x-y)-x3 B.-x(x-2y)2
C.x(4xy-4y2-x2) D.-x(-4xy+4y2+x2)
B
B
5. 若关于 x 的多项式 x2-8x+m2 是完全平方式,则 m 的值为______.
±4
随堂练习
6.分解因式:
(1) x2 + 12x + 36; (2) - 2xy - x2 - y2;
(3) a2 + 2a + 1; (4) 4x2 - 4x + 1;
(5) ax2 + 2a2x + a3; (6) - 3x2 + 6xy - 3y2.
解:(1)(x + 6)2;(2)- (x + y)2;
(3)(a + 1)2;(4)(2x - 1)2;
(5)a(x + a)2;(6)- 3(x - y)2.
随堂练习
7. (1) 已知 a-b=3,求 a(a-2b)+b2 的值;
(2) 已知 ab=2,a+b=5,求 a3b+2a2b2+ab3 的值.
原式=2×52 = 50.
解:(1) 原式=a2-2ab+b2=(a-b)2.
当 a-b=3 时,原式=32=9.
(2) 原式=ab(a2+2ab+b2)=ab(a+b)2.
当 ab=2,a+b=5 时,
课堂小结
完全平方公式分解因式
公式
a2±2ab+b2=(a±b)2
特点
(1)要求多项式有三项.
(2)其中两项同号,且都可以写成某数或式的平方,另一项则是这两数或式的乘积的2倍,符号可正可负.
课后作业
完成教材习题4.5
这节课你学到了什么?谈谈你的收获,
小结与反思
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
