18.2.1.1 矩形的性质 人教版数学八年级下册同步练习(含答案)
文档属性
| 名称 | 18.2.1.1 矩形的性质 人教版数学八年级下册同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 131.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-29 13:56:59 | ||
图片预览

文档简介
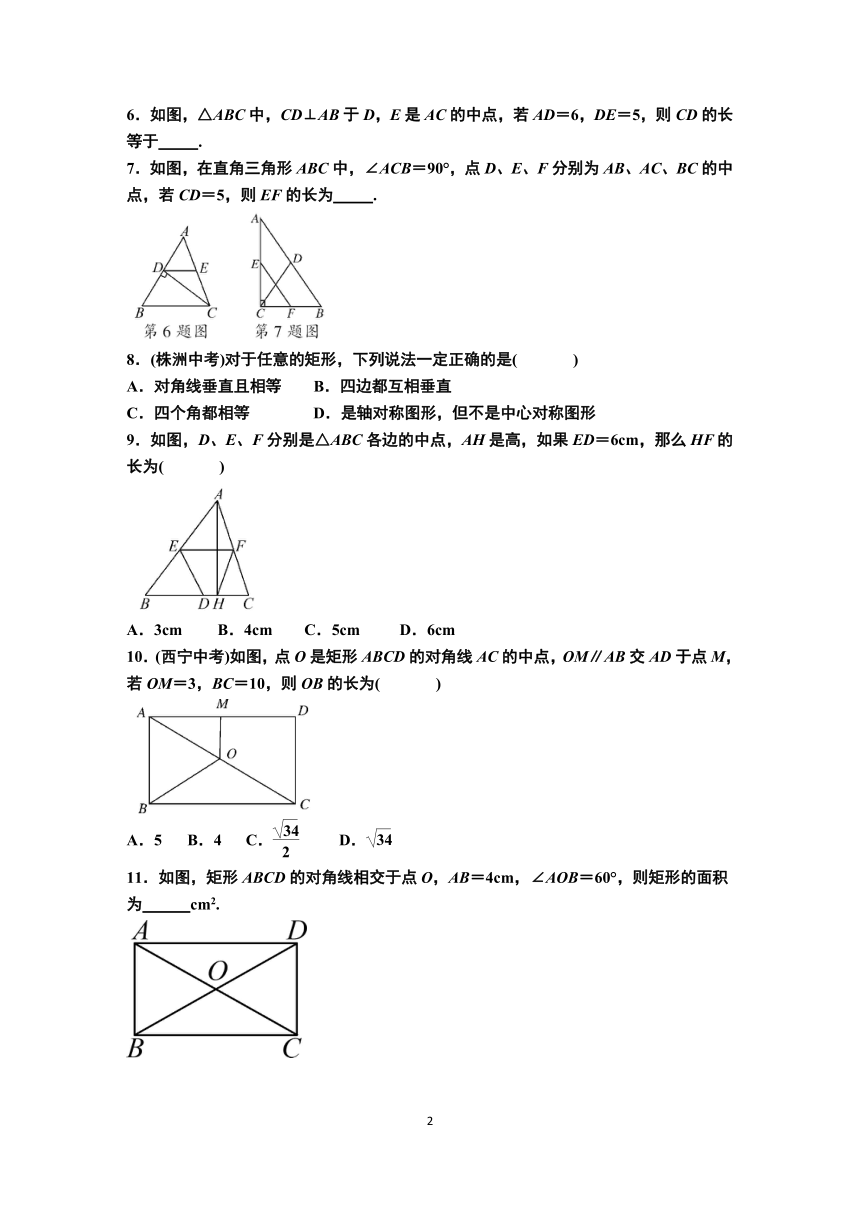
第十八章 平行四边形
18.2.1 矩形
第1课时 矩形的性质
1.矩形具有而一般平行四边形不具有的性质是( )
A.对角相等 B.对边相等 C.对角线相等 D.对角线互相平分
2.(浙江中考)如图,矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在E处,CE交AD于点F,则DF的长等于( )
A. B. C. D.
3.在 ABCD中,若∠A=∠B,则四边形ABCD是 .
4.如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,则∠EAO= .
5.(广西中考)矩形ABCD中,E、F分别是AD、BC的中点,CE、AF分别交BD于G、H两点.求证:
(1)四边形AFCE是平行四边形;
(2)EG=FH.
6.如图,△ABC中,CD⊥AB于D,E是AC的中点,若AD=6,DE=5,则CD的长等于 .
7.如图,在直角三角形ABC中,∠ACB=90°,点D、E、F分别为AB、AC、BC的中点,若CD=5,则EF的长为 .
8.(株洲中考)对于任意的矩形,下列说法一定正确的是( )
A.对角线垂直且相等 B.四边都互相垂直
C.四个角都相等 D.是轴对称图形,但不是中心对称图形
9.如图,D、E、F分别是△ABC各边的中点,AH是高,如果ED=6cm,那么HF的长为( )
A.3cm B.4cm C.5cm D.6cm
10.(西宁中考)如图,点O是矩形ABCD的对角线AC的中点,OM∥AB交AD于点M,若OM=3,BC=10,则OB的长为( )
A.5 B.4 C. D.
11.如图,矩形ABCD的对角线相交于点O,AB=4cm,∠AOB=60°,则矩形的面积为 cm2.
12.如图,已知在矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC.DE=4cm,矩形ABCD的周长为32cm,求AE的长.
13.(玉林中考)如图,在矩形ABCD中,AB=5,AD=3,点P是AB边上一点(不与A、B重合),连接CP,过点P作PQ⊥CP交AD边于点Q,连接CQ.
(1)当△CDQ≌△CPQ时,求AQ的长;
(2)取CQ的中点M,连接MD、MP,若MD⊥MP,求AQ的长.
14.如图,四边形ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.
(1)求证:四边形AECG是平行四边形;
(2)若AB=4cm,BC=3cm,求线段EF的长.
1
参考答案
1. C
2. B
3. 矩形
4. 15°
5. 证明:(1)∵四边形ABCD是矩形,∴AD∥BC,AD=BC,∵E、F分别是AD、BC的中点,∴AE=AD,CF=BC,∴AE=CF,∴四边形AFCE是平行四边形;
(2)∵四边形AFCE是平行四边形,∴CE∥AF,∴∠DGE=∠AHD=∠BHF,∵AD∥CB,∴∠EDG=∠FBH,在△DEG和△BFH中,∴△DEG≌△BFH(AAS),∴EG=FH.
6. 8
7. 5
8. C
9. D
10. D
11. 16
12. 解:∵EF⊥CE,∴∠FEC=90°,∴∠AEF+∠DEC=90°.而∠ECD+∠DEC=90°,∴∠AEF=∠ECD.又∵∠FAE=∠EDC=90°,EF=EC,∴Rt△AEF≌Rt△DCE(AAS),∴AE=CD,∴AD=AE+4,∵矩形ABCD的周长为32cm,∴2(AE+AE+4)=32,解得AE=6cm.
13. 解:(1)∵△CDQ≌△CPQ,∴CP=CD=5,PB==4,故AP=5-4=1,设AQ=x,则PQ=QD=3-x,在Rt△QAP中,QP2=QA2+AP2,即(3-x)2=x2+1,∴x=,∴AQ=;
(2)由题意MD、MP分别是Rt△CDQ与Rt△CPQ共同斜边CQ的中线,∴MD=MC=MP=MQ,∴∠1=2∠2,∠3=2∠4,∠1+∠3=2(∠2+∠4),∴∠2+∠4=(∠1+∠3)=45°,∴∠PCB=90°-45°=45°,∴PB=BC=3,又∠APQ=45°,∴AQ=AP=5-3=2.
14. (1)证明:在矩形ABCD中,∵AD∥BC,∴∠DAC=∠BCA.由题意,得∠GAH=∠DAC,∠ECF=∠BCA,∴∠GAH=∠ECF,∴AG∥CE.又∵AE∥CG,∴四边形AECG是平行四边形;
(2)解:在Rt△ABC中,∵AB=4,BC=3,∴AC=5.∵CF=CB=3,∴AF=2.在Rt△AEF中,设EF=x,则AE=(4-x).根据勾股定理,得AE2=AF2+EF2,即(4-x)2=22+x2,解得x=,即线段EF的长为cm.
18.2.1 矩形
第1课时 矩形的性质
1.矩形具有而一般平行四边形不具有的性质是( )
A.对角相等 B.对边相等 C.对角线相等 D.对角线互相平分
2.(浙江中考)如图,矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在E处,CE交AD于点F,则DF的长等于( )
A. B. C. D.
3.在 ABCD中,若∠A=∠B,则四边形ABCD是 .
4.如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,则∠EAO= .
5.(广西中考)矩形ABCD中,E、F分别是AD、BC的中点,CE、AF分别交BD于G、H两点.求证:
(1)四边形AFCE是平行四边形;
(2)EG=FH.
6.如图,△ABC中,CD⊥AB于D,E是AC的中点,若AD=6,DE=5,则CD的长等于 .
7.如图,在直角三角形ABC中,∠ACB=90°,点D、E、F分别为AB、AC、BC的中点,若CD=5,则EF的长为 .
8.(株洲中考)对于任意的矩形,下列说法一定正确的是( )
A.对角线垂直且相等 B.四边都互相垂直
C.四个角都相等 D.是轴对称图形,但不是中心对称图形
9.如图,D、E、F分别是△ABC各边的中点,AH是高,如果ED=6cm,那么HF的长为( )
A.3cm B.4cm C.5cm D.6cm
10.(西宁中考)如图,点O是矩形ABCD的对角线AC的中点,OM∥AB交AD于点M,若OM=3,BC=10,则OB的长为( )
A.5 B.4 C. D.
11.如图,矩形ABCD的对角线相交于点O,AB=4cm,∠AOB=60°,则矩形的面积为 cm2.
12.如图,已知在矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC.DE=4cm,矩形ABCD的周长为32cm,求AE的长.
13.(玉林中考)如图,在矩形ABCD中,AB=5,AD=3,点P是AB边上一点(不与A、B重合),连接CP,过点P作PQ⊥CP交AD边于点Q,连接CQ.
(1)当△CDQ≌△CPQ时,求AQ的长;
(2)取CQ的中点M,连接MD、MP,若MD⊥MP,求AQ的长.
14.如图,四边形ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.
(1)求证:四边形AECG是平行四边形;
(2)若AB=4cm,BC=3cm,求线段EF的长.
1
参考答案
1. C
2. B
3. 矩形
4. 15°
5. 证明:(1)∵四边形ABCD是矩形,∴AD∥BC,AD=BC,∵E、F分别是AD、BC的中点,∴AE=AD,CF=BC,∴AE=CF,∴四边形AFCE是平行四边形;
(2)∵四边形AFCE是平行四边形,∴CE∥AF,∴∠DGE=∠AHD=∠BHF,∵AD∥CB,∴∠EDG=∠FBH,在△DEG和△BFH中,∴△DEG≌△BFH(AAS),∴EG=FH.
6. 8
7. 5
8. C
9. D
10. D
11. 16
12. 解:∵EF⊥CE,∴∠FEC=90°,∴∠AEF+∠DEC=90°.而∠ECD+∠DEC=90°,∴∠AEF=∠ECD.又∵∠FAE=∠EDC=90°,EF=EC,∴Rt△AEF≌Rt△DCE(AAS),∴AE=CD,∴AD=AE+4,∵矩形ABCD的周长为32cm,∴2(AE+AE+4)=32,解得AE=6cm.
13. 解:(1)∵△CDQ≌△CPQ,∴CP=CD=5,PB==4,故AP=5-4=1,设AQ=x,则PQ=QD=3-x,在Rt△QAP中,QP2=QA2+AP2,即(3-x)2=x2+1,∴x=,∴AQ=;
(2)由题意MD、MP分别是Rt△CDQ与Rt△CPQ共同斜边CQ的中线,∴MD=MC=MP=MQ,∴∠1=2∠2,∠3=2∠4,∠1+∠3=2(∠2+∠4),∴∠2+∠4=(∠1+∠3)=45°,∴∠PCB=90°-45°=45°,∴PB=BC=3,又∠APQ=45°,∴AQ=AP=5-3=2.
14. (1)证明:在矩形ABCD中,∵AD∥BC,∴∠DAC=∠BCA.由题意,得∠GAH=∠DAC,∠ECF=∠BCA,∴∠GAH=∠ECF,∴AG∥CE.又∵AE∥CG,∴四边形AECG是平行四边形;
(2)解:在Rt△ABC中,∵AB=4,BC=3,∴AC=5.∵CF=CB=3,∴AF=2.在Rt△AEF中,设EF=x,则AE=(4-x).根据勾股定理,得AE2=AF2+EF2,即(4-x)2=22+x2,解得x=,即线段EF的长为cm.
