18.2.2.1 菱形的性质 同步练习(含答案)人教版数学八年级下册
文档属性
| 名称 | 18.2.2.1 菱形的性质 同步练习(含答案)人教版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 168.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-29 16:02:56 | ||
图片预览

文档简介
第十八章 平行四边形
18.2.2 菱形
第1课时 菱形的性质
1.(十堰中考)菱形不具备的性质是( )
A.四条边都相等 B.对角线一定相等 C.是轴对称图形 D.是中心对称图形
2.(孝感中考)如图,菱形ABCD的对角线AC、BD相交于点O,AC=10,BD=24,则菱形ABCD的周长为( )
A.52 B.48 C.40 D.20
3.(衢州中考)如图,已知某广场菱形花坛ABCD的周长是24米,∠BAD=60°,则花坛对角线AC的长等于( )
A.6米 B.6米 C.3米 D.3米
4.如图所示,已知菱形ABCD,其顶点A、B在数轴上对应的数分别为-4和1,则BC= .
5.四边形ABCD为菱形,∠BAD=60°,AB=6,对角线AC与BD相交于点O,点E在AC上,若OE=,则CE的长度为 .
6.(沈阳中考)如图,在菱形ABCD中,过点D作DE⊥AB于点E,作DF⊥BC于点F,连接EF,求证:
(1)△ADE≌△CDF;
(2)∠BEF=∠BFE.
7.(徐州中考)若菱形两条对角线的长分别是6cm和8cm,则周长为 ,面积为 cm2.
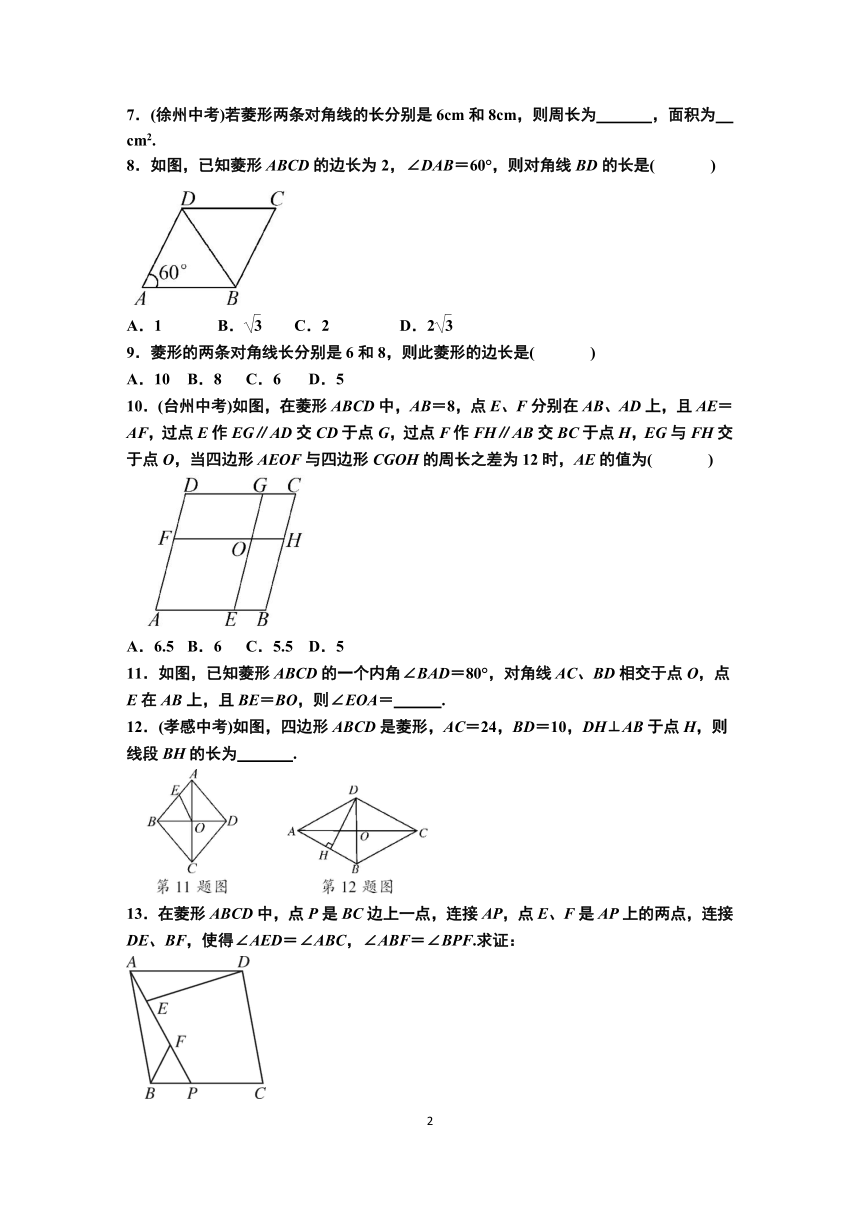
8.如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是( )
A.1 B. C.2 D.2
9.菱形的两条对角线长分别是6和8,则此菱形的边长是( )
A.10 B.8 C.6 D.5
10.(台州中考)如图,在菱形ABCD中,AB=8,点E、F分别在AB、AD上,且AE=AF,过点E作EG∥AD交CD于点G,过点F作FH∥AB交BC于点H,EG与FH交于点O,当四边形AEOF与四边形CGOH的周长之差为12时,AE的值为( )
A.6.5 B.6 C.5.5 D.5
11.如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC、BD相交于点O,点E在AB上,且BE=BO,则∠EOA= .
12.(孝感中考)如图,四边形ABCD是菱形,AC=24,BD=10,DH⊥AB于点H,则线段BH的长为 .
13.在菱形ABCD中,点P是BC边上一点,连接AP,点E、F是AP上的两点,连接DE、BF,使得∠AED=∠ABC,∠ABF=∠BPF.求证:
14.已知,如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接EC.
(1)求证:AE=EC;
(2)当∠ABC=60°,∠CEF=60°时,点F在线段BC上的什么位置?说明理由.
15.如图,在边长为10的菱形ABCD中,对角线BD=16,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.
1
参考答案
1-3 BAA
4. 5
5. 4或2
6. 证明:(1)∵菱形ABCD,∴AD=CD,∠A=∠C,∵DE⊥AB,DF⊥BC,∴∠AED=∠CFD=90°,∴△ADE≌△CDF(AAS);
(2)∵菱形ABCD,∴AB=CB,∵△ADE≌△CDF,∴AE=CF,∴BE=BF,∴∠BEF=∠BFE.
7. 20cm 24
8-10 CDC
11. 25°
12.
13. 证明:(1)∵四边形ABCD是菱形,∴AB=AD,AD∥BC,∴∠BPF=∠DAE,∵∠ABC=∠AED,∴∠BAF=∠ADE,∵∠ABF=∠BPF,∠BPA=∠DAE,∴∠ABF=∠DAE,∵AB=DA,∴△ABF≌△DAE(ASA);
(2)∵△ABF≌△DAE,∴AE=BF,DE=AF,∵AF=AE+EF=BF+EF,∴DE=BF+EF.
14. (1)证明:连接AC,∵BD是菱形ABCD的对角线,∴BD垂直平分AC,∴AE=EC;
(2)解:点F是线段BC的中点,理由如下:在菱形ABCD中,AB=BC,又∵∠ABC=60°,∴△ABC是等边三角形,∴∠BAC=60°,∵AE=EC,∠CEF=60°,∴∠EAC=30°=∠BAC,∴AF是△ABC的角平分线,∵AF交BC于F,∴AF是△ABC的BC边上的中线,∴点F是线段BC的中点.
15. 解:(1)12,96;
(2)如图③,连接AO,连接AC交BD于点G,则S△ABD=S△ABO+S△ADO,∴BD·AG=AB·OE+AD·OF,即×16×6=×10·OE+×10·OF,解得OE+OF=9.6,是定值,不变;
(3)如图④,连接AO,连接AC交BD于点G,则S△ABD=S△ABO-S△ADO,∴BD·AG=AB·OE-AD·OF,即×16×6=×10·OE-×10·OF,解得OE-OF=9.6,是定值,不变,∴OE+OF的值变化.OE、OF之间的数量关系为:OE-OF=9.6.
18.2.2 菱形
第1课时 菱形的性质
1.(十堰中考)菱形不具备的性质是( )
A.四条边都相等 B.对角线一定相等 C.是轴对称图形 D.是中心对称图形
2.(孝感中考)如图,菱形ABCD的对角线AC、BD相交于点O,AC=10,BD=24,则菱形ABCD的周长为( )
A.52 B.48 C.40 D.20
3.(衢州中考)如图,已知某广场菱形花坛ABCD的周长是24米,∠BAD=60°,则花坛对角线AC的长等于( )
A.6米 B.6米 C.3米 D.3米
4.如图所示,已知菱形ABCD,其顶点A、B在数轴上对应的数分别为-4和1,则BC= .
5.四边形ABCD为菱形,∠BAD=60°,AB=6,对角线AC与BD相交于点O,点E在AC上,若OE=,则CE的长度为 .
6.(沈阳中考)如图,在菱形ABCD中,过点D作DE⊥AB于点E,作DF⊥BC于点F,连接EF,求证:
(1)△ADE≌△CDF;
(2)∠BEF=∠BFE.
7.(徐州中考)若菱形两条对角线的长分别是6cm和8cm,则周长为 ,面积为 cm2.
8.如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是( )
A.1 B. C.2 D.2
9.菱形的两条对角线长分别是6和8,则此菱形的边长是( )
A.10 B.8 C.6 D.5
10.(台州中考)如图,在菱形ABCD中,AB=8,点E、F分别在AB、AD上,且AE=AF,过点E作EG∥AD交CD于点G,过点F作FH∥AB交BC于点H,EG与FH交于点O,当四边形AEOF与四边形CGOH的周长之差为12时,AE的值为( )
A.6.5 B.6 C.5.5 D.5
11.如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC、BD相交于点O,点E在AB上,且BE=BO,则∠EOA= .
12.(孝感中考)如图,四边形ABCD是菱形,AC=24,BD=10,DH⊥AB于点H,则线段BH的长为 .
13.在菱形ABCD中,点P是BC边上一点,连接AP,点E、F是AP上的两点,连接DE、BF,使得∠AED=∠ABC,∠ABF=∠BPF.求证:
14.已知,如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接EC.
(1)求证:AE=EC;
(2)当∠ABC=60°,∠CEF=60°时,点F在线段BC上的什么位置?说明理由.
15.如图,在边长为10的菱形ABCD中,对角线BD=16,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.
1
参考答案
1-3 BAA
4. 5
5. 4或2
6. 证明:(1)∵菱形ABCD,∴AD=CD,∠A=∠C,∵DE⊥AB,DF⊥BC,∴∠AED=∠CFD=90°,∴△ADE≌△CDF(AAS);
(2)∵菱形ABCD,∴AB=CB,∵△ADE≌△CDF,∴AE=CF,∴BE=BF,∴∠BEF=∠BFE.
7. 20cm 24
8-10 CDC
11. 25°
12.
13. 证明:(1)∵四边形ABCD是菱形,∴AB=AD,AD∥BC,∴∠BPF=∠DAE,∵∠ABC=∠AED,∴∠BAF=∠ADE,∵∠ABF=∠BPF,∠BPA=∠DAE,∴∠ABF=∠DAE,∵AB=DA,∴△ABF≌△DAE(ASA);
(2)∵△ABF≌△DAE,∴AE=BF,DE=AF,∵AF=AE+EF=BF+EF,∴DE=BF+EF.
14. (1)证明:连接AC,∵BD是菱形ABCD的对角线,∴BD垂直平分AC,∴AE=EC;
(2)解:点F是线段BC的中点,理由如下:在菱形ABCD中,AB=BC,又∵∠ABC=60°,∴△ABC是等边三角形,∴∠BAC=60°,∵AE=EC,∠CEF=60°,∴∠EAC=30°=∠BAC,∴AF是△ABC的角平分线,∵AF交BC于F,∴AF是△ABC的BC边上的中线,∴点F是线段BC的中点.
15. 解:(1)12,96;
(2)如图③,连接AO,连接AC交BD于点G,则S△ABD=S△ABO+S△ADO,∴BD·AG=AB·OE+AD·OF,即×16×6=×10·OE+×10·OF,解得OE+OF=9.6,是定值,不变;
(3)如图④,连接AO,连接AC交BD于点G,则S△ABD=S△ABO-S△ADO,∴BD·AG=AB·OE-AD·OF,即×16×6=×10·OE-×10·OF,解得OE-OF=9.6,是定值,不变,∴OE+OF的值变化.OE、OF之间的数量关系为:OE-OF=9.6.
