2023-2024学年度北师大版数学九年级下册1.4解直角三角形 课件(共28张PPT)
文档属性
| 名称 | 2023-2024学年度北师大版数学九年级下册1.4解直角三角形 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-29 15:13:38 | ||
图片预览






文档简介
(共28张PPT)
1.4 解直角三角形
1.了解解直角三角形的含义;
2.经历解直角三角形的过程,掌握解直角三角形的方法.
学习目标
难点
重点
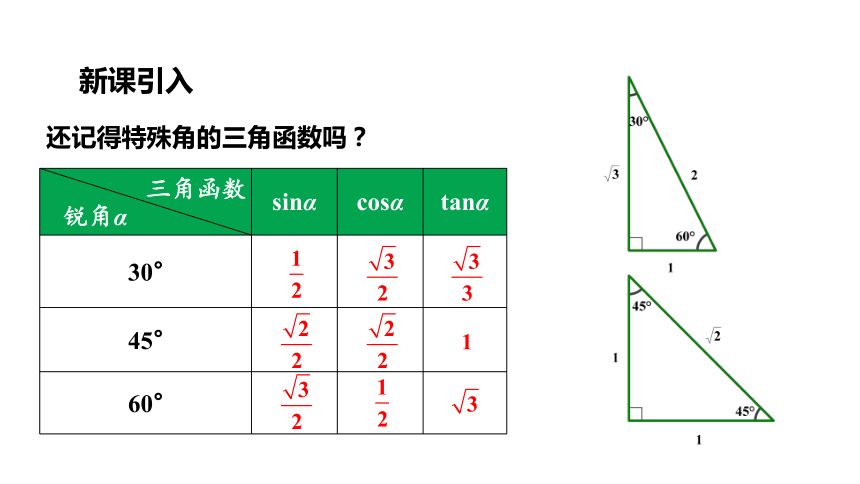
sinα cosα tanα
30°
45°
60°
三角函数
锐角α
还记得特殊角的三角函数吗?
新课引入
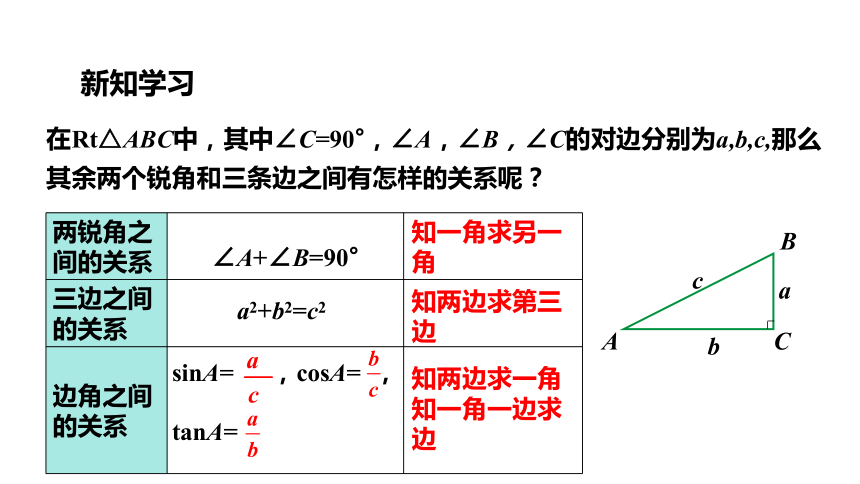
在Rt△ABC中,其中∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,那么其余两个锐角和三条边之间有怎样的关系呢?
A
C
B
c
b
a
两锐角之间的关系
三边之间的关系
边角之间的关系
知两边求一角
知一角一边求边
知一角求另一角
知两边求第三边
∠A+∠B=90°
a2+b2=c2
sinA= ,cosA= ,tanA=
新知学习
什么叫解直角三角形?
一般地,在直角三角形中,除直角外,共有五个元素,即三条边和两个锐角,由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
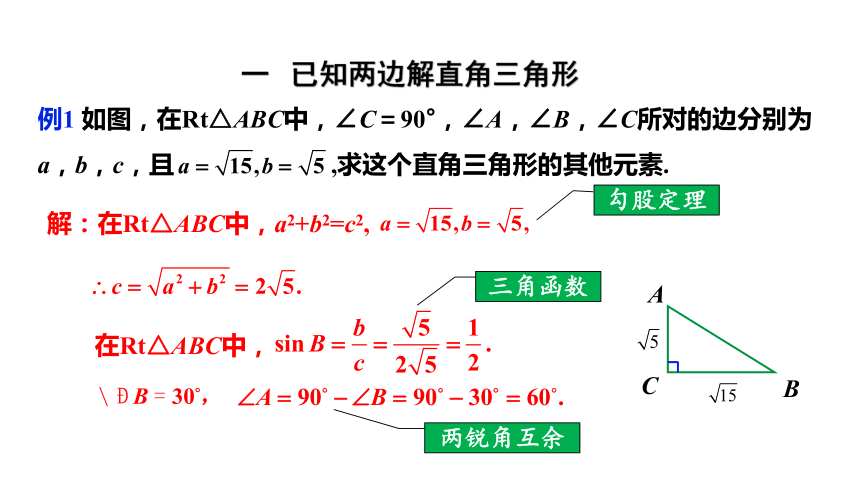
例1 如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且 ,求这个直角三角形的其他元素.
A
B
C
解:在Rt△ABC中,a2+b2=c2,
在Rt△ABC中,
勾股定理
三角函数
两锐角互余
一 已知两边解直角三角形
例1 如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且 ,求这个直角三角形的其他元素.
A
B
C
还有其他方法吗?
温馨提示
解直角三角形时,求某些未知量的方法往往不唯一,选择关系式通常遵循以下原则:
1.为了减少误差,尽量选择可以直接应用原始数据的关系式;
2.尽量选择便于计算的关系式;
3.能用乘法计算的要避免使用除法计算.
二 已知一边及一锐角解直角三角形
在Rt△ABC中,如果已知一边和一锐角,你能求出这个三角形的其他元素吗?
例2 如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且b=30,∠B=25°,求这个直角三角形的其他元素(sin25°=0.423,cos25°=0.906,tan25°=0.466,边长精确到1).
A
B
C
b
30
c
a
25°
解:在Rt△ABC中,∠C=90°,∠B=25°,
∴∠A=65°.
两锐角互余
三角函数
三角函数
例2 如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且b=30,∠B=25°,求这个直角三角形的其他元素(sin25°=0.423,cos25°=0.906,tan25°=0.466,边长精确到1).
A
B
C
b
30
c
a
25°
还有其他方法吗?
归纳
事实上,在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.
1.在△ABC中,∠C=90°,若∠B=2∠A,b=3,则a等于( )
A.
B.
C.6
D.
B
A
B
C
b=3
a
随堂练习
2.如图,在 Rt△ABC 中,∠C = 90° ,AC = ,BC = ,解这个三角形.
A
C
B
解: ,
分析:给了两条边的长,没有已知的锐角.
可以先求第三条边,也可以先求角
3. 在Rt△ABC中, ∠C=90° , ∠A,∠B,∠C所对的边分别为a, b, c,根据下列条 件求出直角三角形的其他元素:
(sin27°=0.454,cos27°=0.891,tan27°=0.510,角度精确到1°)
(1) 已知 a = 4, b =8;
∵∠C=90°,∴∠B=90°-∠A≈63°.
解:在Rt△ABC 中,由勾股定理得 c= = .
∵sin A= = = , ∴∠A≈27°.
A
B
C
b=8
a=4
由勾股定理得a= = .
解:在Rt△ABC中,∠C=90°,∠B=60°,
∴∠A=30°.
∴c= = = .
(2) 已知 b =10, ∠B=60°;
∵sin B= ,b=10,
A
B
C
b=10
60°
a
c
(3) 已知 c =20, ∠A=60°;
解:在Rt△ABC中,∠C=90°,∠A=60°,
∴∠B=30°.
∵sin A= ,c=20,
∴a=c·sin A=20×sin 60°=20× = .
由勾股定理得b= =10.
B
A
C
c=20
60°
a
b
4. 如图,工件上有一V形槽(AC=BC),测得它的上口宽20mm,深19.2mm,求V形角∠ACB的度数(tan27.5°=0.521,结果精确到1°)
解:过点C作CD⊥AB与点D,
∵AC =BC,CD⊥AB,
在Rt△ADC中,∠ADC=90°,AD=10,DC=19.2.
(2)当梯子底端距离墙面2.4m时,梯子与地面所成的锐角α等于多少 这时人是否能够安全使用这个梯子 (精确到1°)
5. 要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所形成的角α一般要满足50°≤α≤75°,现有一个长6m的梯子,问:
(sin50°=0.77,sin66°=0.91,cos66°=0.41,sin75°=0.97)
(1)使用这个梯子最高可以安全攀上多高的墙 (精确到0.1m)
5. 要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所形成的角α一般要满足50°≤α≤75°,现有一个长6m的梯子,问:
(1)使用这个梯子最高可以安全攀上多高的墙 (精确到0.1m)
解:(1)当∠BAC=75°时,梯子能安全使用且它的顶端最高,
BC=AB·sin∠BAC=6sin75°≈5.8
答:安全使用这个梯子时,梯子的顶端距离地面的最大高度约为5.8m.
在Rt△ABC中,有sin∠BAC
5. 要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所形成的角α一般要满足50°≤α≤75°,现有一个长6m的梯子,问:
(2)当梯子底端距离墙面2.4m时,梯子与地面所成的锐角α等于多少 这时人是否能够安全使用这个梯子 (精确到1°)
∴∠BAC≈66°,
∵50°≤66°≤75°
∴α等于66°,这时人安全.
解:(2)在Rt△ABC中,有cos∠BAC
6. (真实问题情景)如图①为某银行人工自助终端机,图②是其侧面结构示意图,已知控制板的长
解:如解图,过点
解图
过点
答:点
解图
7.(选做题)学习了解直角三角形的相关知识,掌握了利用锐角三角函数的定义来解决直角三角形的问题,还掌握了通过作高来解决斜三角形(即锐角三角形与钝角三角形)的问题以及相关的实际应用问题.下面请同学们利用这些学习经验,应用类比的方法来解决下面的新问题.定义:如图1,在△ABC中,AB=AC,我们称它的腰与底的长度之比为顶角∠A的余对( csdA ),记作csdA=
(l)填空:csd60°=______;csd90°=______ ;
csd120°= ______
1
(2)如图2,在Rt△ABC中,∠C=90°, cosA= ,求csdA的值.
( 2 )如图2中,过点C作CH⊥AB于点H,在AB上截取AF,使得AF=AC .
∵cosA =
∴可以假设AC=4k,AB=5k,则BC=3k,
∵cosA =
∴
H
∴CH=
∴FH=AF-AH=4k- =
∴CF=
∴
H
课堂小结
A
C
B
c
b
a
两锐角之间的关系
三边之间的关系
边角之间的关系
知两边求一角
知一角一边求边
知一角求另一角
知两边求第三边
∠A+∠B=90°
a2+b2=c2
sinA= ,cosA= ,tanA=
1.4 解直角三角形
1.了解解直角三角形的含义;
2.经历解直角三角形的过程,掌握解直角三角形的方法.
学习目标
难点
重点
sinα cosα tanα
30°
45°
60°
三角函数
锐角α
还记得特殊角的三角函数吗?
新课引入
在Rt△ABC中,其中∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,那么其余两个锐角和三条边之间有怎样的关系呢?
A
C
B
c
b
a
两锐角之间的关系
三边之间的关系
边角之间的关系
知两边求一角
知一角一边求边
知一角求另一角
知两边求第三边
∠A+∠B=90°
a2+b2=c2
sinA= ,cosA= ,tanA=
新知学习
什么叫解直角三角形?
一般地,在直角三角形中,除直角外,共有五个元素,即三条边和两个锐角,由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
例1 如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且 ,求这个直角三角形的其他元素.
A
B
C
解:在Rt△ABC中,a2+b2=c2,
在Rt△ABC中,
勾股定理
三角函数
两锐角互余
一 已知两边解直角三角形
例1 如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且 ,求这个直角三角形的其他元素.
A
B
C
还有其他方法吗?
温馨提示
解直角三角形时,求某些未知量的方法往往不唯一,选择关系式通常遵循以下原则:
1.为了减少误差,尽量选择可以直接应用原始数据的关系式;
2.尽量选择便于计算的关系式;
3.能用乘法计算的要避免使用除法计算.
二 已知一边及一锐角解直角三角形
在Rt△ABC中,如果已知一边和一锐角,你能求出这个三角形的其他元素吗?
例2 如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且b=30,∠B=25°,求这个直角三角形的其他元素(sin25°=0.423,cos25°=0.906,tan25°=0.466,边长精确到1).
A
B
C
b
30
c
a
25°
解:在Rt△ABC中,∠C=90°,∠B=25°,
∴∠A=65°.
两锐角互余
三角函数
三角函数
例2 如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,且b=30,∠B=25°,求这个直角三角形的其他元素(sin25°=0.423,cos25°=0.906,tan25°=0.466,边长精确到1).
A
B
C
b
30
c
a
25°
还有其他方法吗?
归纳
事实上,在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.
1.在△ABC中,∠C=90°,若∠B=2∠A,b=3,则a等于( )
A.
B.
C.6
D.
B
A
B
C
b=3
a
随堂练习
2.如图,在 Rt△ABC 中,∠C = 90° ,AC = ,BC = ,解这个三角形.
A
C
B
解: ,
分析:给了两条边的长,没有已知的锐角.
可以先求第三条边,也可以先求角
3. 在Rt△ABC中, ∠C=90° , ∠A,∠B,∠C所对的边分别为a, b, c,根据下列条 件求出直角三角形的其他元素:
(sin27°=0.454,cos27°=0.891,tan27°=0.510,角度精确到1°)
(1) 已知 a = 4, b =8;
∵∠C=90°,∴∠B=90°-∠A≈63°.
解:在Rt△ABC 中,由勾股定理得 c= = .
∵sin A= = = , ∴∠A≈27°.
A
B
C
b=8
a=4
由勾股定理得a= = .
解:在Rt△ABC中,∠C=90°,∠B=60°,
∴∠A=30°.
∴c= = = .
(2) 已知 b =10, ∠B=60°;
∵sin B= ,b=10,
A
B
C
b=10
60°
a
c
(3) 已知 c =20, ∠A=60°;
解:在Rt△ABC中,∠C=90°,∠A=60°,
∴∠B=30°.
∵sin A= ,c=20,
∴a=c·sin A=20×sin 60°=20× = .
由勾股定理得b= =10.
B
A
C
c=20
60°
a
b
4. 如图,工件上有一V形槽(AC=BC),测得它的上口宽20mm,深19.2mm,求V形角∠ACB的度数(tan27.5°=0.521,结果精确到1°)
解:过点C作CD⊥AB与点D,
∵AC =BC,CD⊥AB,
在Rt△ADC中,∠ADC=90°,AD=10,DC=19.2.
(2)当梯子底端距离墙面2.4m时,梯子与地面所成的锐角α等于多少 这时人是否能够安全使用这个梯子 (精确到1°)
5. 要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所形成的角α一般要满足50°≤α≤75°,现有一个长6m的梯子,问:
(sin50°=0.77,sin66°=0.91,cos66°=0.41,sin75°=0.97)
(1)使用这个梯子最高可以安全攀上多高的墙 (精确到0.1m)
5. 要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所形成的角α一般要满足50°≤α≤75°,现有一个长6m的梯子,问:
(1)使用这个梯子最高可以安全攀上多高的墙 (精确到0.1m)
解:(1)当∠BAC=75°时,梯子能安全使用且它的顶端最高,
BC=AB·sin∠BAC=6sin75°≈5.8
答:安全使用这个梯子时,梯子的顶端距离地面的最大高度约为5.8m.
在Rt△ABC中,有sin∠BAC
5. 要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所形成的角α一般要满足50°≤α≤75°,现有一个长6m的梯子,问:
(2)当梯子底端距离墙面2.4m时,梯子与地面所成的锐角α等于多少 这时人是否能够安全使用这个梯子 (精确到1°)
∴∠BAC≈66°,
∵50°≤66°≤75°
∴α等于66°,这时人安全.
解:(2)在Rt△ABC中,有cos∠BAC
6. (真实问题情景)如图①为某银行人工自助终端机,图②是其侧面结构示意图,已知控制板的长
解:如解图,过点
解图
过点
答:点
解图
7.(选做题)学习了解直角三角形的相关知识,掌握了利用锐角三角函数的定义来解决直角三角形的问题,还掌握了通过作高来解决斜三角形(即锐角三角形与钝角三角形)的问题以及相关的实际应用问题.下面请同学们利用这些学习经验,应用类比的方法来解决下面的新问题.定义:如图1,在△ABC中,AB=AC,我们称它的腰与底的长度之比为顶角∠A的余对( csdA ),记作csdA=
(l)填空:csd60°=______;csd90°=______ ;
csd120°= ______
1
(2)如图2,在Rt△ABC中,∠C=90°, cosA= ,求csdA的值.
( 2 )如图2中,过点C作CH⊥AB于点H,在AB上截取AF,使得AF=AC .
∵cosA =
∴可以假设AC=4k,AB=5k,则BC=3k,
∵cosA =
∴
H
∴CH=
∴FH=AF-AH=4k- =
∴CF=
∴
H
课堂小结
A
C
B
c
b
a
两锐角之间的关系
三边之间的关系
边角之间的关系
知两边求一角
知一角一边求边
知一角求另一角
知两边求第三边
∠A+∠B=90°
a2+b2=c2
sinA= ,cosA= ,tanA=
