2023-2024学年度北师大版数学九年级下册1.5三角函数的应用 课件(共29张PPT)
文档属性
| 名称 | 2023-2024学年度北师大版数学九年级下册1.5三角函数的应用 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 609.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-29 15:17:02 | ||
图片预览






文档简介
(共29张PPT)
1.5 三角函数的应用
1.经历应用三角函数解决实际问题的过程,进一步体会三角函数在解决问题过程中的作用.
2.正确理解方位角、仰角和坡角的概念;
3.能运用解直角三角形知识解决方位角、仰角和坡角的问题.
4.能够把实际问题转化为数学问题,能够借助计算器进行有关三角函数的计算,并能进一步对结果的意义进行说明.
学习目标
难点
重点
新课引入
泰坦尼克号叙述了一段浪漫凄美的爱情故事,泰坦尼克号的沉没让人感到遗憾,如果舵手能够分清方向、准确的计算距离,避开冰山,也许“泰坦尼克号”的结局是完美的.
那你知道如何结合方位角等数据进行计算,帮助轮船在航行中远离危险吗?
30°
45°
B
O
A
东
西
北
南
北偏东30°
南偏西45°
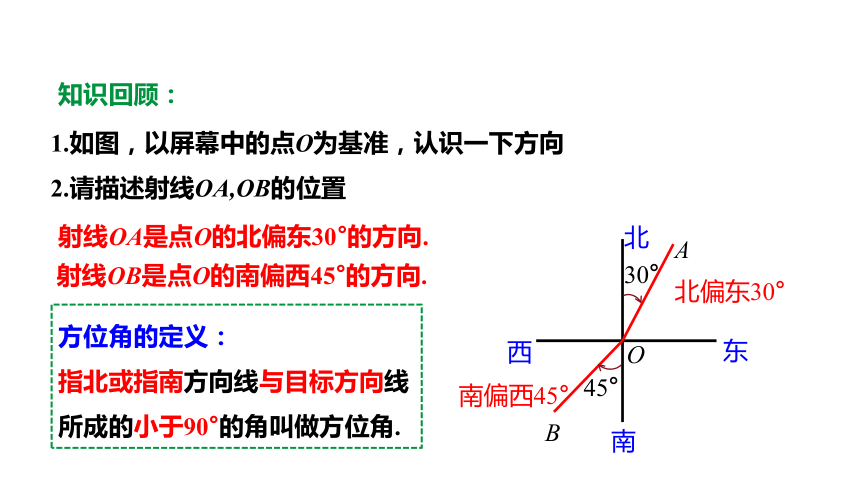
1.如图,以屏幕中的点O为基准,认识一下方向
2.请描述射线OA,OB的位置
射线OA是点O的北偏东30°的方向.
射线OB是点O的南偏西45°的方向.
方位角的定义:
指北或指南方向线与目标方向线所成的小于90°的角叫做方位角.
知识回顾:
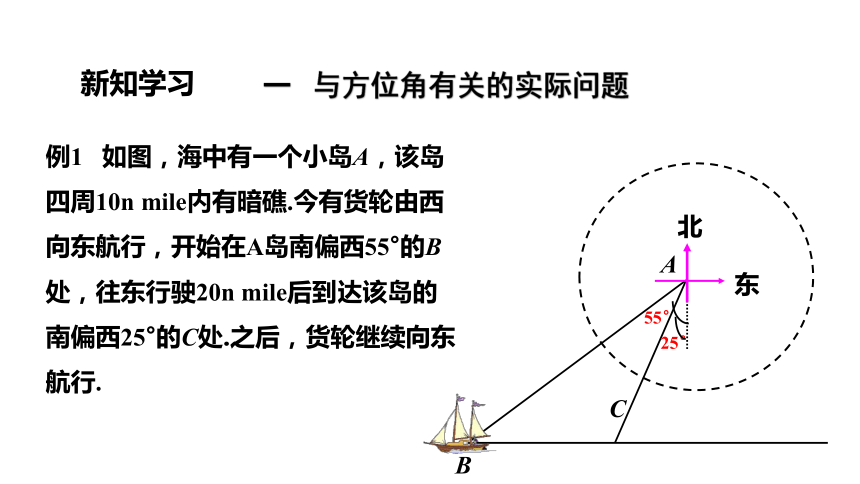
例1 如图,海中有一个小岛A,该岛四周10n mile内有暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20n mile后到达该岛的南偏西25°的C处.之后,货轮继续向东航行.
A
B
C
东
北
55°
25°
一 与方位角有关的实际问题
新知学习
你认为货轮继续向东航行途中会有触礁的危险吗?你是怎样想的?与同伴进行交流.
A
B
C
东
北
55°
25°
【分析】这船继续向东航行是否安全,取决于灯塔C 到AB航线的距离是否大于 10 n mile.
20
55°
25°
A
B
C
D
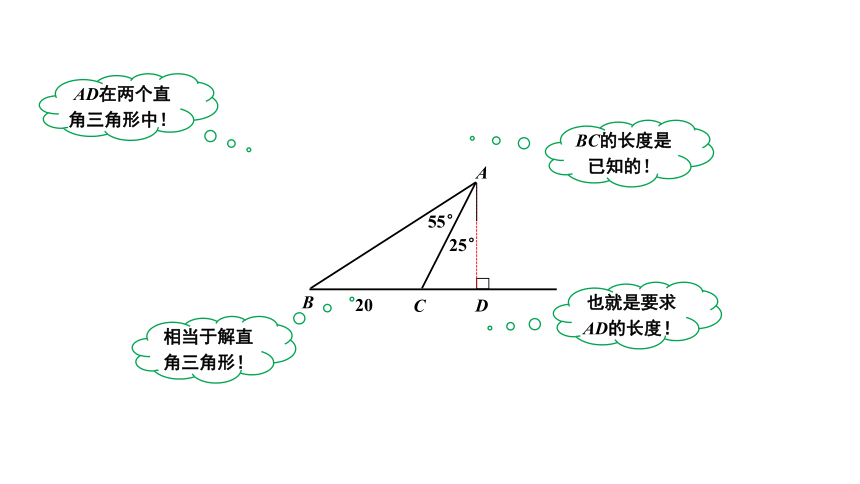
也就是要求AD的长度!
AD在两个直角三角形中!
相当于解直角三角形!
BC的长度是已知的!
解:如解图,由点A作AD⊥BC于点D,
则在Rt△ABD中,
在Rt△ACD中,
解得
答:货轮继续向东航行途中没有触礁的危险.
由BC=BD-CD,得
20
55°
25°
A
B
C
D
x
设AD=x,
1.将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
2.根据条件的特点,适当选用锐角三角形函数等去解直角三角形;
3.得到数学问题的答案;
4.得到实际问题的答案.
归纳
利用解直角三角形的知识解决实际问题的一般过程是:
仰角:在视线与水平线所成的夹角中,视线在水平线上方的角
俯角:在视线与水平线所成的夹角中,视线在水平线下方的角
二 仰角和俯角问题
水平线
O
视线
仰角
铅垂线
视线
俯角
例2 如图所示,为了测量山高AC,在水平点B处测得山顶A的仰角是( )
A. ∠A
B.∠ABC
C. ∠ABD
D.以上都不对
方法总结:弄清仰角的概念.找到视线与水平线所成的夹角
B
仰角:在视线与水平线所成的央角中,
视线在水平线上方的角
例3 如图,小明想测量塔 CD 的高度.他在 A 处仰望塔顶,测得仰角为30°,再往塔的方向前进 50 m 至 B 处,测得仰角为60°,那么该塔有多高?(小明的身高忽略不计,结果精确到 1 m )
D
A
B
C
┌
50 m
30°
60°
也就是要求CD的长度!
CD在两个直角三角形中!
相当于解直角三角形!
AB的长度是已知的!
D
A
B
C
┌
50 m
30°
60°
答:该塔约有 43 m 高.
解:如解图,设CD =x m,
由题意:∠A=30°,∠DBC=60°,AB =50 m. 则∠ADC =60°,∠BDC =30°.
D
A
B
C
┌
50 m
30°
60°
在修路、挖河、开渠和筑坝时,设计图纸上都要注明斜坡的倾斜程度.
如图所示,坡面的铅垂高度 ( h ) 和水平长度 ( l ) 的比叫做坡面的坡度 ( 或坡比 ),记作 i, 即 i = h:l . 坡度通常写成 1:m 的形式,如 i = 1:6 .
坡面与水平面的夹角叫做坡角,记作 α .
α
l
h
坡面
i = h : l
三 利用坡角解决实际问题
温馨提示
对于坡度有 . 坡度等于坡角的正切值
显然,坡度越大,坡角 α 就越大,坡面就越陡.
α
l
h
坡面
i = h : l
例4 某商场准备改善原有楼梯的安全性能,把倾角由原来的40°减至35°,如图.已知原楼梯的长度为4 m,调整后的楼梯会加长多少?楼梯多占多长一段地面 (sin35°=0.57,cos35°=0.82,tan35°=0.70,sin40°=0.64,cos40°=0.77,tan40°=0.84,结果精确到0.01m).
楼梯什么量不变?
你能画出图吗?
要求什么量?
哪些量是已知的?
C
B
A
D
┌
4 m
35°
40°
调整后的楼梯会加长多少?
调整后的楼梯会加长多少?
分析:如图,根据题意可知∠A=35°,∠BDC=40°,DB=4 m, 求
AB-BD的长.
答:调整后的楼梯会加长约 0.48 m.
解:∵
C
B
A
D
┌
4 m
35°
40°
分析:如图,根据题意可知∠A =35°,∠BDC =40°,DB =4 m,求 AD 的长.
楼梯多占多长一段地面
C
B
A
D
┌
4 m
35°
40°
答:楼梯多占约 0.61 m 长的一段地面.
解:
C
B
A
D
┌
4 m
35°
40°
1.如图,一灯柱AB被一钢缆CD固定.CD与地面成40°夹角,且DB=5 m.现再在C点上方 2 m 处加固另一根钢缆ED,那么钢缆 ED 的长度为多少?(sin40°=0.64,cos40°=0.77,tan40°=0.84,结果精确到0.01m).
答:钢缆 DE 的长度约为 7.96 m.
解:
2 m
40°
5 m
随堂练习
2.如图,水库大坝的截面是梯形ABCD,其中AD∥BC,坝顶AD=6 m,
坡长CD=8 m,坡底BC = 30 m,∠ADC=135°.
(1)求坡面AB的坡比;
(2)如果坝长100 m,那么修建这个大坝共需多少土石料
(结果精确到0.01m3 )
A
B
C
D
(1)求坡面AB的坡比;
A
B
C
D
6 m
8 m
30 m
135°
E
┐
F
┌
解:如解图,过点 D 作 DE⊥BC 于点 E,过点A作AF⊥BC于点F ,
答:坡比约为 0.31.
则
(2)如果坝长100 m,那么修建这个大坝共需多少土石料 (结果精确到0.01m3 )
100 m
A
B
C
D
6 m
30 m
F
┌
答:修建这个大坝共需土石料约10 182.34 m3.
解:如解图,由梯形面积公式 得
3.如图①是一种折叠式可调节钓鱼竿支架,图②是其示意图,AB是地插,用来将支架固定在地面AF上,支架AB可绕点A转动,用来调节AB与地面AF的夹角,支架CD可绕支点C转动,用来调节CD与AB的夹角,支架CD可伸缩调节长度.已知BC=60cm,钓鱼竿DB始终与地面AF平行.
(1)如图②,当支架CD与地面AF垂直时,CD=40 cm,求∠BAF的度数;
解:(1 )在Rt△BDC中,∠CDB=90°, sin∠CBD=
∵BC= 60cm,CD=40cm,
∴sin∠CBD= ≈0.667,
∴∠CBD≈41.8 °,
∵BD// AF,
∴∠BAF= ∠CBD≈41.8 °
(2)如图③,若保持支架AB与地面的夹角不变,调节支架CD与AB的夹角,使得∠DCB=90°,求此时支架CD的长度. (结果保留小数点后1位参考数据sin41.8°≈0.667 cos41.8° ≈0.745, ≈2.236)
(2)设CD=2xcm, 在Rt△BDC中,∠DCB=90°, sin∠CBD=
则BD=3xcm,
由勾股定理得: BC2+CD2=BD2,即602+(2x) 2=(3x) 2,
解得: x1=12 ≈26.83, x2=-12 (舍去),
∴CD=2x≈53.7 (cm),
答:支架CD的长度约为53.7cm.
1.将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
2.根据条件的特点,适当选用锐角三角函数等去解直角三角形;
3.得到数学问题的答案;
4.得到实际问题的答案.
利用解直角三角形的知识解决实际问题的一般过程是:
课堂小结
1.5 三角函数的应用
1.经历应用三角函数解决实际问题的过程,进一步体会三角函数在解决问题过程中的作用.
2.正确理解方位角、仰角和坡角的概念;
3.能运用解直角三角形知识解决方位角、仰角和坡角的问题.
4.能够把实际问题转化为数学问题,能够借助计算器进行有关三角函数的计算,并能进一步对结果的意义进行说明.
学习目标
难点
重点
新课引入
泰坦尼克号叙述了一段浪漫凄美的爱情故事,泰坦尼克号的沉没让人感到遗憾,如果舵手能够分清方向、准确的计算距离,避开冰山,也许“泰坦尼克号”的结局是完美的.
那你知道如何结合方位角等数据进行计算,帮助轮船在航行中远离危险吗?
30°
45°
B
O
A
东
西
北
南
北偏东30°
南偏西45°
1.如图,以屏幕中的点O为基准,认识一下方向
2.请描述射线OA,OB的位置
射线OA是点O的北偏东30°的方向.
射线OB是点O的南偏西45°的方向.
方位角的定义:
指北或指南方向线与目标方向线所成的小于90°的角叫做方位角.
知识回顾:
例1 如图,海中有一个小岛A,该岛四周10n mile内有暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20n mile后到达该岛的南偏西25°的C处.之后,货轮继续向东航行.
A
B
C
东
北
55°
25°
一 与方位角有关的实际问题
新知学习
你认为货轮继续向东航行途中会有触礁的危险吗?你是怎样想的?与同伴进行交流.
A
B
C
东
北
55°
25°
【分析】这船继续向东航行是否安全,取决于灯塔C 到AB航线的距离是否大于 10 n mile.
20
55°
25°
A
B
C
D
也就是要求AD的长度!
AD在两个直角三角形中!
相当于解直角三角形!
BC的长度是已知的!
解:如解图,由点A作AD⊥BC于点D,
则在Rt△ABD中,
在Rt△ACD中,
解得
答:货轮继续向东航行途中没有触礁的危险.
由BC=BD-CD,得
20
55°
25°
A
B
C
D
x
设AD=x,
1.将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
2.根据条件的特点,适当选用锐角三角形函数等去解直角三角形;
3.得到数学问题的答案;
4.得到实际问题的答案.
归纳
利用解直角三角形的知识解决实际问题的一般过程是:
仰角:在视线与水平线所成的夹角中,视线在水平线上方的角
俯角:在视线与水平线所成的夹角中,视线在水平线下方的角
二 仰角和俯角问题
水平线
O
视线
仰角
铅垂线
视线
俯角
例2 如图所示,为了测量山高AC,在水平点B处测得山顶A的仰角是( )
A. ∠A
B.∠ABC
C. ∠ABD
D.以上都不对
方法总结:弄清仰角的概念.找到视线与水平线所成的夹角
B
仰角:在视线与水平线所成的央角中,
视线在水平线上方的角
例3 如图,小明想测量塔 CD 的高度.他在 A 处仰望塔顶,测得仰角为30°,再往塔的方向前进 50 m 至 B 处,测得仰角为60°,那么该塔有多高?(小明的身高忽略不计,结果精确到 1 m )
D
A
B
C
┌
50 m
30°
60°
也就是要求CD的长度!
CD在两个直角三角形中!
相当于解直角三角形!
AB的长度是已知的!
D
A
B
C
┌
50 m
30°
60°
答:该塔约有 43 m 高.
解:如解图,设CD =x m,
由题意:∠A=30°,∠DBC=60°,AB =50 m. 则∠ADC =60°,∠BDC =30°.
D
A
B
C
┌
50 m
30°
60°
在修路、挖河、开渠和筑坝时,设计图纸上都要注明斜坡的倾斜程度.
如图所示,坡面的铅垂高度 ( h ) 和水平长度 ( l ) 的比叫做坡面的坡度 ( 或坡比 ),记作 i, 即 i = h:l . 坡度通常写成 1:m 的形式,如 i = 1:6 .
坡面与水平面的夹角叫做坡角,记作 α .
α
l
h
坡面
i = h : l
三 利用坡角解决实际问题
温馨提示
对于坡度有 . 坡度等于坡角的正切值
显然,坡度越大,坡角 α 就越大,坡面就越陡.
α
l
h
坡面
i = h : l
例4 某商场准备改善原有楼梯的安全性能,把倾角由原来的40°减至35°,如图.已知原楼梯的长度为4 m,调整后的楼梯会加长多少?楼梯多占多长一段地面 (sin35°=0.57,cos35°=0.82,tan35°=0.70,sin40°=0.64,cos40°=0.77,tan40°=0.84,结果精确到0.01m).
楼梯什么量不变?
你能画出图吗?
要求什么量?
哪些量是已知的?
C
B
A
D
┌
4 m
35°
40°
调整后的楼梯会加长多少?
调整后的楼梯会加长多少?
分析:如图,根据题意可知∠A=35°,∠BDC=40°,DB=4 m, 求
AB-BD的长.
答:调整后的楼梯会加长约 0.48 m.
解:∵
C
B
A
D
┌
4 m
35°
40°
分析:如图,根据题意可知∠A =35°,∠BDC =40°,DB =4 m,求 AD 的长.
楼梯多占多长一段地面
C
B
A
D
┌
4 m
35°
40°
答:楼梯多占约 0.61 m 长的一段地面.
解:
C
B
A
D
┌
4 m
35°
40°
1.如图,一灯柱AB被一钢缆CD固定.CD与地面成40°夹角,且DB=5 m.现再在C点上方 2 m 处加固另一根钢缆ED,那么钢缆 ED 的长度为多少?(sin40°=0.64,cos40°=0.77,tan40°=0.84,结果精确到0.01m).
答:钢缆 DE 的长度约为 7.96 m.
解:
2 m
40°
5 m
随堂练习
2.如图,水库大坝的截面是梯形ABCD,其中AD∥BC,坝顶AD=6 m,
坡长CD=8 m,坡底BC = 30 m,∠ADC=135°.
(1)求坡面AB的坡比;
(2)如果坝长100 m,那么修建这个大坝共需多少土石料
(结果精确到0.01m3 )
A
B
C
D
(1)求坡面AB的坡比;
A
B
C
D
6 m
8 m
30 m
135°
E
┐
F
┌
解:如解图,过点 D 作 DE⊥BC 于点 E,过点A作AF⊥BC于点F ,
答:坡比约为 0.31.
则
(2)如果坝长100 m,那么修建这个大坝共需多少土石料 (结果精确到0.01m3 )
100 m
A
B
C
D
6 m
30 m
F
┌
答:修建这个大坝共需土石料约10 182.34 m3.
解:如解图,由梯形面积公式 得
3.如图①是一种折叠式可调节钓鱼竿支架,图②是其示意图,AB是地插,用来将支架固定在地面AF上,支架AB可绕点A转动,用来调节AB与地面AF的夹角,支架CD可绕支点C转动,用来调节CD与AB的夹角,支架CD可伸缩调节长度.已知BC=60cm,钓鱼竿DB始终与地面AF平行.
(1)如图②,当支架CD与地面AF垂直时,CD=40 cm,求∠BAF的度数;
解:(1 )在Rt△BDC中,∠CDB=90°, sin∠CBD=
∵BC= 60cm,CD=40cm,
∴sin∠CBD= ≈0.667,
∴∠CBD≈41.8 °,
∵BD// AF,
∴∠BAF= ∠CBD≈41.8 °
(2)如图③,若保持支架AB与地面的夹角不变,调节支架CD与AB的夹角,使得∠DCB=90°,求此时支架CD的长度. (结果保留小数点后1位参考数据sin41.8°≈0.667 cos41.8° ≈0.745, ≈2.236)
(2)设CD=2xcm, 在Rt△BDC中,∠DCB=90°, sin∠CBD=
则BD=3xcm,
由勾股定理得: BC2+CD2=BD2,即602+(2x) 2=(3x) 2,
解得: x1=12 ≈26.83, x2=-12 (舍去),
∴CD=2x≈53.7 (cm),
答:支架CD的长度约为53.7cm.
1.将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
2.根据条件的特点,适当选用锐角三角函数等去解直角三角形;
3.得到数学问题的答案;
4.得到实际问题的答案.
利用解直角三角形的知识解决实际问题的一般过程是:
课堂小结
