1.6利用三角函数测高课件(共27张PPT)2023-2024学年度北师大版数学九年级下册

(共27张PPT)
1.6 利用三角函数测高
九年级下
北师版
1.经历设计活动方案、自制仪器和运用仪器进行实地测量以及撰写活动报告的过程；
2.能够对所得的数据进行整理、分析和矫正；
3.能够综合运用直角三角形边角关系的知识解决实际问题．
学习目标
难点
重点
如果不告诉你这些高楼大厦的高度，你能想到办法测出它们的高度吗？
新课引入
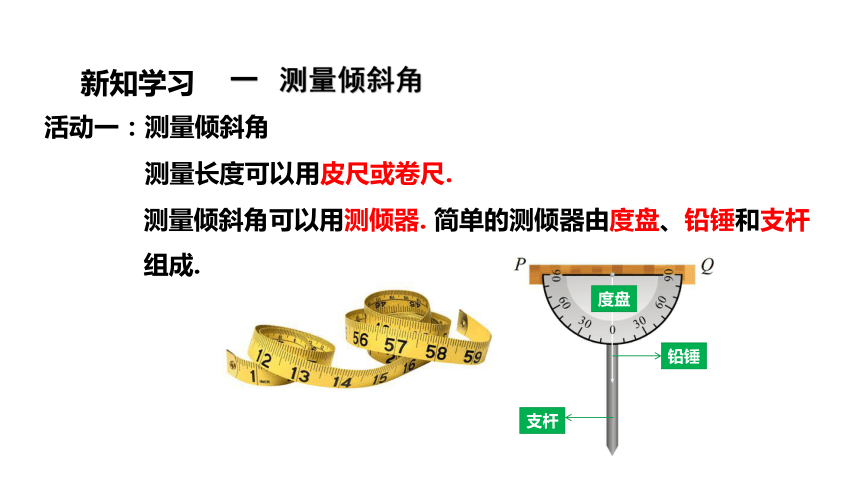
一 测量倾斜角
活动一：测量倾斜角
测量倾斜角可以用测倾器. 简单的测倾器由度盘、铅锤和支杆
组成.
测量长度可以用皮尺或卷尺.
度盘
铅锤
支杆
新知学习
使用测倾器测量倾斜角的步骤如下：
1.把支杆竖直插入地面，使支杆的中心线、铅垂线和度盘的 0° 刻度线重合，这时度盘的顶线 PQ 在水平位置.
2.转动度盘，使度盘的直径对准目标M，记下此时铅垂线所指的度数.
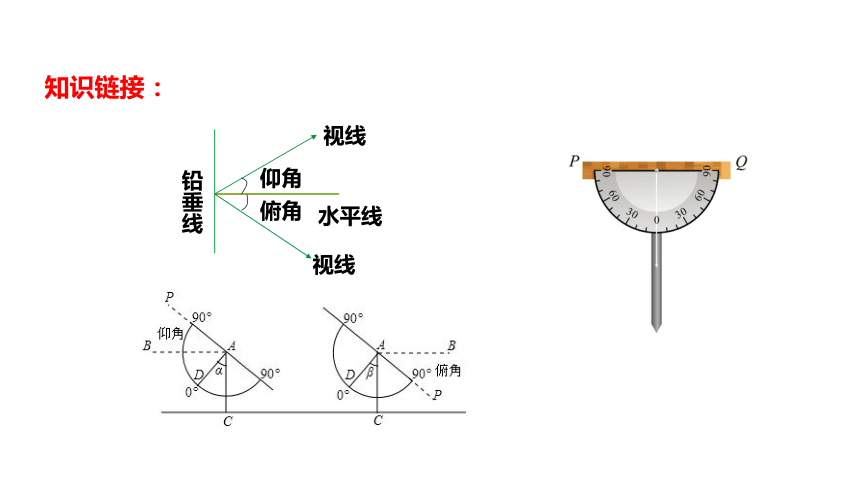
铅垂线
仰角
俯角
水平线
视线
视线
知识链接：
二 测量底部可以到达的物体的高度
所谓“底部可以到达”，就是在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离.
活动二：测量底部可以到达的物体的高度
分组活动、小组合作：
1.你们能设计一个方案测量底部可以到达的物体的高度吗？
2.需要用到哪些工具？
3.需要测量哪些数据？
4.根据测量数据，如何计算物体的高度？
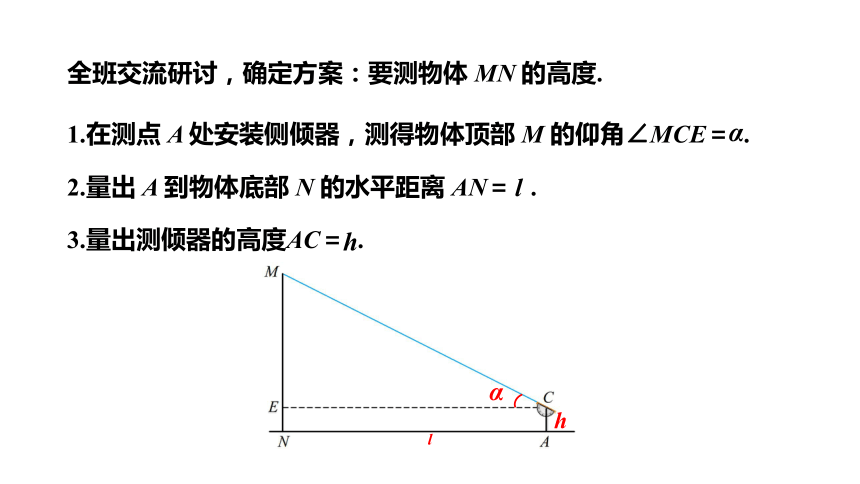
全班交流研讨，确定方案：要测物体 MN 的高度.
1.在测点 A 处安装侧倾器，测得物体顶部 M 的仰角∠MCE＝ .
2.量出 A 到物体底部 N 的水平距离 AN＝ .
3.量出测倾器的高度AC＝ .
在Rt△CEM 中，
如图，由题意可得CE=AN=l，NE=AC=h.
三 测量底部不可以到达的物体的高度
所谓“底部不可以到达”，就是在地面上不能直接测得测点与被测物体的底部之间的距离.
活动三：测量底部不可以到达的物体的高度
分组活动、小组合作：
1.你们能设计一个方案测量底部不可以到达的物体的高度吗？
2.需要用到哪些工具？
3.需要测量哪些数据？
4.根据测量数据，如何计算物体的高度？
全班交流研讨，确定方案：要测物体 MN 的高度.
1.在测点 A 处安装侧倾器，测得此时M 的仰角∠MCE＝
2.在测点 A与物体之间的B处安置侧倾器（A，B与N 在一条直线上，且A，B之间距离可以直接测得），测得此时M 的仰角∠MDE＝
3.量出测倾器的高度AC＝BD＝ ，以及测点A，B之间的距离AB＝
如图，在Rt△CEM中，
在Rt△DEM中，
由 得，
例1 文字是文明传承的载体和见证，中国文字博物馆通过荟萃历代中国文字样本精华，展示中华民族灿烂的文化和辉煌的文明.如图是中国文字博物馆门口屹立着的字坊，某中学数学兴趣小组想通过自己所学的锐角三角函数知识测量该字坊 的高度，甲同学站在字坊正前方 ，通过测角仪测得字坊顶端 的仰角为 ，乙同学通过测角仪在字坊背面 处测得字坊顶端 的仰角为 ，已知测角仪的高度 ， 均为 ，甲同学与乙同学之间的直线距离 为 ，
点 ， ， 在同一竖直平面内.
求字坊 的高度.(结果精确到 ，参考数据： ， ， ， )
M
解：如解图，连接 交 于点 ，易得四边形 ， ， 是矩形，
， ，
∵在 中， ，
.
∵在 中， ， ,
，
，
，解得 ，
.
答：字坊 的高度约为 .
M
例2 为了测量教学大楼的高度，三个数学小组设计了不同的方案，测量方案与数据如下表:
课题 测量教学大楼 的高度 测量工具 测量角度的仪器，皮尺 测量小组 第一组 第二组 第三组
测量方案示意图
说明 点 ， ， 在同一条直线上 是教学大楼正西方向的“校训石” ，借助 进行测量，使 ， ， 三点在同一条直线上， ， ， 三点在同一条直线上 是教学大楼旁居民住宅楼
测量数据 ， ， 米 ， ， 米 ，
(1) 根据测量方案和所得数据，第_____组的数据无法算出大楼高度；
三
(2) 请选择其中一个可行方案及其测量数据，求出教学大楼的高度.(结果保留整数.参考数据： ， ， )
解：方案一：选择第一组的测量数据，
由题意得， ， ， ，
是等腰直角三角形， ，
设 ，则 ， ,
，
解得 ，
答：教学大楼 的高度约为15米.
方案二：选择第二组的测量数据，
由题意得， ，
，
，设 ，则 ， ，
，
，
解得 ，
答：教学大楼 的高度约为15米.
1. 在“测量旗杆的高度”的数学课题学习中，某学习小组测得太阳光线与水平面的夹角为27°(tan 27°≈0.51)，此时旗杆在水平地面上的影子的长度为24 m，则旗杆的高度约为( )
A．24 m B．20 m C．16 m D．12 m
D
随堂练习
2. 如图，建筑物BC上有一杆AB，从与BC相距10 m的D处观测旗杆顶部A的仰角为53°，观测旗杆底部B的仰角为45°，则旗杆AB的高度约为 m.(结果取整数，参考数据：sin 53°≈0.80，cos 53°≈0.60，tan 53°≈1.33)
3. 如图，两建筑物的水平距离BC为18 m,从点A测得点D的俯角α为30°，测得点C的俯角β为60°，则建筑物CD的高度为______m.(结果保留根号)
3
3. 某中学组织学生前往革命老区开展红色游学，进一步了解中国共产党的奋斗历程，增强爱国主义教育.在一处革命先烈纪念碑 的山脚下 处沿着台阶向上行走到达山顶平台边缘 ，已知斜坡 的坡角为 ，斜坡 长106米，点 离纪念碑中心 的距离为8.3米，用无人机在纪念碑顶部 测得山脚底点 的俯角是 ，求纪念碑的高度.(结果精确到1米，参考数据： ， ，
， )
解：如图，过点 作 点水平线的垂线，垂足为点 ，延长 交水平线 于点 ，
∴四边形 为矩形， 米， ，
在 中， ，
， 米，
E
F
(米)，
(米)，
在 中， ， ，
(米)，
，

(米) ．
答：纪念碑的高度约为21米．
E
F
测量底部不可以到达的物体的高度
（两次测量仰角）
测倾器的认识及使用
利用三角
函数测高
测量底部可以到达的物体的高度
（一次测量仰角）
课堂小结