2.1.4 多项式的乘法(第2课时) 课件(共28张PPT)
文档属性
| 名称 | 2.1.4 多项式的乘法(第2课时) 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:36:40 | ||
图片预览





文档简介
(共28张PPT)
2.1.4 多项式的乘法
第2课时 多项式与多项式相乘
1.在具体情境中了解多项式乘法的意义,会利用法则进行简单的多项式乘法运算.
2.经历探索多项式与多项式乘法法则的过程,理解多项式与多项式相乘的运算算理,体会乘法分配律的作用及转化思想在解决问题过程中的应用,发展学生有条理的思考和语言表达能力.
3.在解决问题的过程中了解数学的价值,发展“用数学”的信心.
【教学重点】熟悉多项式与多项式乘法法则.
【教学难点】理解多项式与多项式相乘的算理.
我们学了“幂的运算性质”有哪些?
同底数幂的乘法:
am·an = am+n
幂的乘方:
(am)n=amn
(m、n 都是正整数)
积的乘方:
(ab)n=anbn
1. 如何进行单项式与多项式乘法的运算?
② 再把所得的积相加.
① 将单项式分别乘多项式的各项;
2. 进行单项式与多项式乘法运算时,要注意什么
① 不能漏乘:
即单项式要乘遍多项式的每一项;
② 去括号时注意符号的确定.
请同学们阅读课本P38的内容:
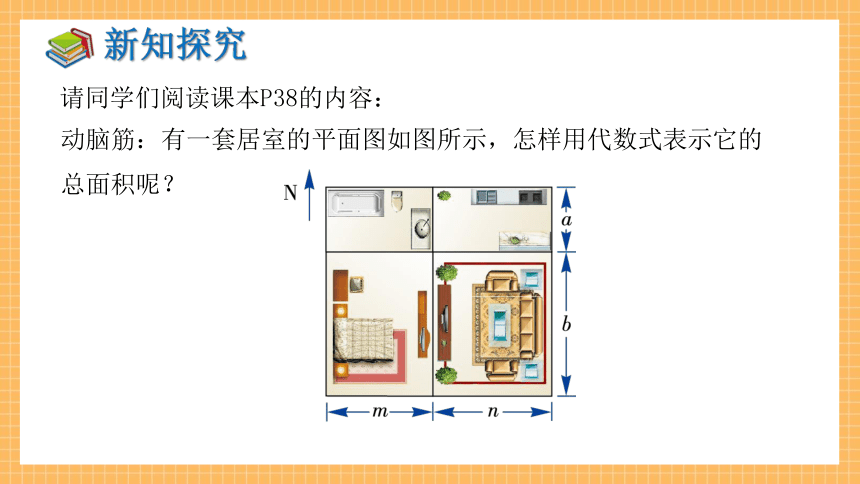
动脑筋:有一套居室的平面图如图所示,怎样用代数式表示它的总面积呢?
有一套居室的平面图如图所示,怎样用代数式表示它的总面积呢?
南北向总长为 a + b,东西向总长为 m+ n,所以居室的总面积为:
(a+b)·(m+n)
整体计算
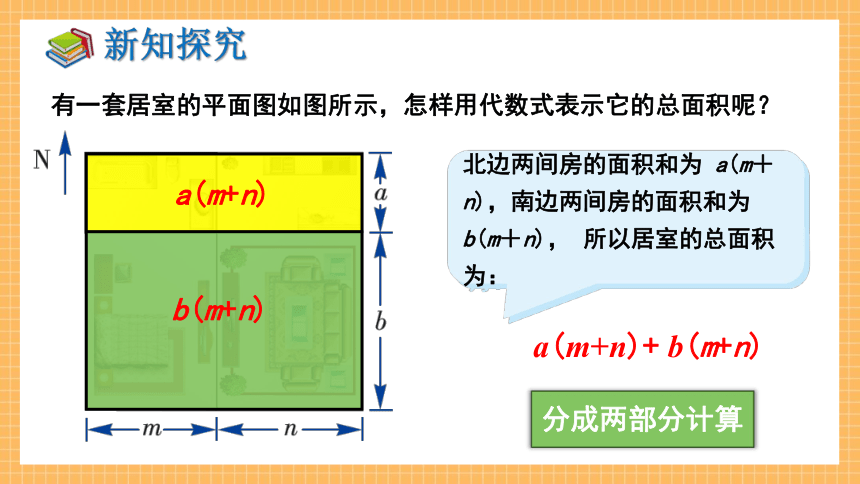
有一套居室的平面图如图所示,怎样用代数式表示它的总面积呢?
a(m+n)
a(m+n)+ b(m+n)
北边两间房的面积和为 a(m+n),南边两间房的面积和为 b(m+n), 所以居室的总面积为:
b(m+n)
分成两部分计算
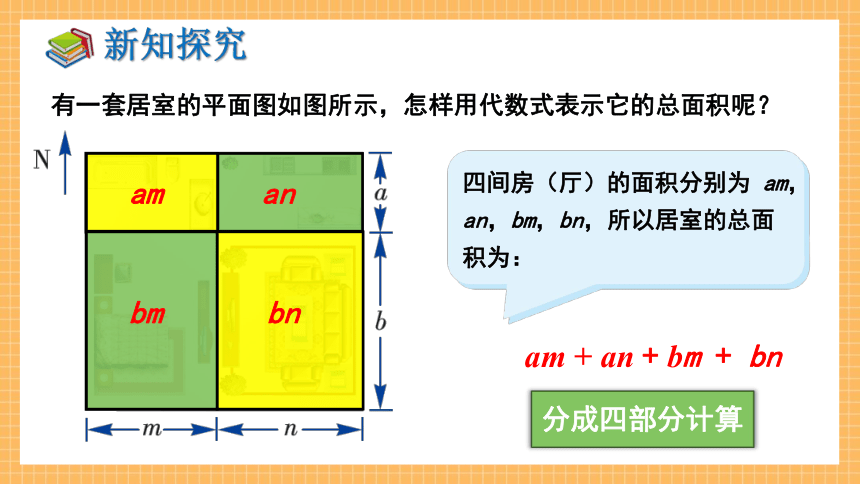
有一套居室的平面图如图所示,怎样用代数式表示它的总面积呢?
四间房(厅)的面积分别为 am, an,bm,bn,所以居室的总面积为:
am
am + an + bm + bn
an
bm
bn
分成四部分计算
上面的三个代数式都正确表示了该居室的总面积,因此有:
( a+b )( m+n ) = a(m+n) +b( m+n ) = am+an+bm+bn.
撇开上述式子的实际意义,想一想,这几个代数式为什么相等呢?它们利用了乘法运算的什么性质?事实上,由代数式①到代数式②,是把m+n看成一个整体,利用乘法分配律得到a( m+n )+b( m+n ),继续利用乘法分配律,就得到结果am+an+bm+bn.这个运算过程可表示为:
多项式与多项式相乘,先用一个多项式的每一项分别乘另一个多项式的每一项,再把所得的积相加.
多项式乘多项式
1
2
3
4
(a + b)(m + n)
=
am
1
2
3
4
+ an
+ bm
+ bn
多乘多顺口溜:
多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.
【例1】计算:
(1)( 2x + y )( x – 3y );
(2)( 2x + 1 )( 3x2 – x – 5 );
(3)( x + a )( x + b ).
解 (1)( 2x + y )( x -3y )
= 2x · x + 2x ·(-3y)+ y · x + y ·(-3y)
= 2x2-6xy + yx -3y2
= 2x2- 5xy -3y2
(2)( 2x + 1 )( 3x2 - x – 5 )
= 6x3 - 2x2 – 10x + 3x2 – x - 5
= 6x3 + x2 - 11x - 5.
【例1】计算:
(1)( 2x + y )( x – 3y );
(2)( 2x + 1 )( 3x2 – x – 5 );
(3)( x + a )( x + b ).
(3) ( x + a )( x + b )
= x2 + bx + ax + ab
= x2 + ( a + b )x + ab
第(3)小题的直观意义如图
【例1】计算:
(1)( 2x + y )( x – 3y );
(2)( 2x + 1 )( 3x2 – x – 5 );
(3)( x + a )( x + b ).
1、计算:
(1) (1-x)(0.6-x);(2) (2x+y)(x-y);(3) (x + y)(x2-xy + y2).
解:(1) 原式 = 1×0.6-1×x-x · 0.6 + x · x
= 0.6-x-0.6x + x2
= 0.6-1.6x + x2.
(2) 原式 = 2x·x-2x · y + y · x- y · y
= 2x2-2xy + xy-y2
= 2x2-xy-y2.
解:原式 = x · x2-x · xy + xy2 + x2y-xy2 + y · y2
= x3-x2y + xy2 + x2y-xy2 + y3
= x3 + y3.
注意:(1) 漏乘;(2) 符号问题;(3) 最后结果应
化成最简形式 (是同类项的要合并).
(3) (x + y)(x2-xy + y2).
【例2】计算:(1)( a+b )( a-b );
(2)( a+b )2;
(3)( a-b )2.
解:(1)( a+b )( a-b )=a2-ab+ba-b2=a2-b2.
(2)( a+b )2=( a+b )( a-b )=a2+ab+ba+b2=a2+2ab+b2.
(3)( a-b )2=( a-b )( a-b )=a2-ab-ba+b2.
2、先化简,再求值:(a-2b)(a2+2ab+4b2)-a(a-5b)(a+3b),其中 a=-1,b=1.
解:原式=a3-8b3-(a2-5ab)(a+3b)
=a3-8b3-a3-3a2b+5a2b+15ab2
=-8b3+2a2b+15ab2.
当 a=-1,b=1 时,原式=-8+2-15=-21.
方法总结:化简求值的题型,一般应先化简,再
求值,而不是先代值,再计算.
1. 下列计算对不对? 如果不对, 应怎样改正?
(1)( 3a-b )( 2a + b ) = 3a·2a + ( - b )·b = 6a2- b2;
(2) ( x + 3 ) ( 1 - x ) = x·1 + x·x + 3 - 3·x = x2 - 2x + 3 .
解:(1)不对,应为 ( 3a-b )( 2a + b ) = 3a·2a + 3a·b - b ·2a - b ·b = 6a2 + ab - b2 ;
(2)不对,应为 ( x + 3 ) ( 1 - x )= x·1- x·x + 3×1-3·x = x - x2 + 3-3x = -x2-2x + 3
2.判断下列解法是否正确,若不正确请说出理由.
解:原式
解:原式
3. 计算:
(1)(x-2)(x+3);
(2)(x+1)(x+5);
(3)(x+4)(x-5);
(4)(x-3)2;
= x2+x-6
= x2+6x+5
= x2-x-20
= x2-6x+9.
(5)(x+2y)2;
(6)(m-2n)(2m+n);
(7)(3a+2b)(3a-2b);
(8)(3a-2b)2.
= x2+4xy+4y2
= 2m2-3mn-2n2
= 9a2-4b2
= 9a2-12ab+4b2.
4. 计算:
(1)( x-2 )( x + 3 ) ;(2) ( x + 1 ) ( x + 5 ) ;
(3)( x + 4 )( x - 5 );(4)( x - 3 )2.
解:(1)( x-2 )( x + 3 ) = x2 +3x-2x-6 = x2 + x-6;
(2) ( x + 1 ) ( x + 5 ) = x2 + 6x + 5;
(3)( x + 4 )( x - 5 )= x2-5x + 4x-20 = x2-x-20
(4)( x - 3 )2 = ( x - 3 ) ( x - 3 ) = x2-3x+9 = x2-6x+9
5.计算:(1) (x 3y)(x + 7y); (2) (2x + 5y)(3x 2y).
= x2 + 4xy 21y2.
解:(1) 原式 = x2 + 7xy 3yx 21y2
(2) 原式 = 2x 3x 2x 2y + 5 y 3x 5y 2y
= 6x2 4xy + 15xy 10y2
= 6x2 + 11xy 10y2.
6. 计算:
(1)( x + 2y )2 ; (2) ( m – 2n ) ( 2m + n ) ;
(3)( 3a + 2b )( 3a – 2b ); (4)( 3a – 2b )2.
解:(1)(x+2y)2= (x+2y) (x+2y)=x2+2xy+2xy+4y2=x2+4xy+4y2;
(2) (m–2n) (2m+n)=2m2+mn-4mn-2n2=2m2-3mn-2n2
(3)( 3a + 2b )( 3a – 2b )=9a2-4b2
(4)( 3a – 2b )2 = (3a–2b) (3a–2b ) = 9a2-6ab-6ab+4b2 = 9a2-12ab+4b2
7. 化简求值:(4x + 3y)(4x-3y) + (2x + y)(3x-5y),其中 x = 1,y =-2.
解:原式 =
当 x = 1,y = -2 时,
原式 = 22×12-7×1×(-2)-14×(-2)2
= 22 + 14-56 = -20.
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式中的每一项,再把所得的积相加.
注意:
(1)多项式与多项式相乘的结果仍是多项式;
(2)结果的项数应该是原两个多项式项数的积(没有合并同类 项之前),检验项数常常作为检验解题过程是否的有效方法.
(3)多项式与多项式相乘的结果中,要把同类项合并;
多项式乘法法则:
1. 习题2.1中第8、9、10、11题.
2.完成同步练习册中本课时的练习.
2.1.4 多项式的乘法
第2课时 多项式与多项式相乘
1.在具体情境中了解多项式乘法的意义,会利用法则进行简单的多项式乘法运算.
2.经历探索多项式与多项式乘法法则的过程,理解多项式与多项式相乘的运算算理,体会乘法分配律的作用及转化思想在解决问题过程中的应用,发展学生有条理的思考和语言表达能力.
3.在解决问题的过程中了解数学的价值,发展“用数学”的信心.
【教学重点】熟悉多项式与多项式乘法法则.
【教学难点】理解多项式与多项式相乘的算理.
我们学了“幂的运算性质”有哪些?
同底数幂的乘法:
am·an = am+n
幂的乘方:
(am)n=amn
(m、n 都是正整数)
积的乘方:
(ab)n=anbn
1. 如何进行单项式与多项式乘法的运算?
② 再把所得的积相加.
① 将单项式分别乘多项式的各项;
2. 进行单项式与多项式乘法运算时,要注意什么
① 不能漏乘:
即单项式要乘遍多项式的每一项;
② 去括号时注意符号的确定.
请同学们阅读课本P38的内容:
动脑筋:有一套居室的平面图如图所示,怎样用代数式表示它的总面积呢?
有一套居室的平面图如图所示,怎样用代数式表示它的总面积呢?
南北向总长为 a + b,东西向总长为 m+ n,所以居室的总面积为:
(a+b)·(m+n)
整体计算
有一套居室的平面图如图所示,怎样用代数式表示它的总面积呢?
a(m+n)
a(m+n)+ b(m+n)
北边两间房的面积和为 a(m+n),南边两间房的面积和为 b(m+n), 所以居室的总面积为:
b(m+n)
分成两部分计算
有一套居室的平面图如图所示,怎样用代数式表示它的总面积呢?
四间房(厅)的面积分别为 am, an,bm,bn,所以居室的总面积为:
am
am + an + bm + bn
an
bm
bn
分成四部分计算
上面的三个代数式都正确表示了该居室的总面积,因此有:
( a+b )( m+n ) = a(m+n) +b( m+n ) = am+an+bm+bn.
撇开上述式子的实际意义,想一想,这几个代数式为什么相等呢?它们利用了乘法运算的什么性质?事实上,由代数式①到代数式②,是把m+n看成一个整体,利用乘法分配律得到a( m+n )+b( m+n ),继续利用乘法分配律,就得到结果am+an+bm+bn.这个运算过程可表示为:
多项式与多项式相乘,先用一个多项式的每一项分别乘另一个多项式的每一项,再把所得的积相加.
多项式乘多项式
1
2
3
4
(a + b)(m + n)
=
am
1
2
3
4
+ an
+ bm
+ bn
多乘多顺口溜:
多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.
【例1】计算:
(1)( 2x + y )( x – 3y );
(2)( 2x + 1 )( 3x2 – x – 5 );
(3)( x + a )( x + b ).
解 (1)( 2x + y )( x -3y )
= 2x · x + 2x ·(-3y)+ y · x + y ·(-3y)
= 2x2-6xy + yx -3y2
= 2x2- 5xy -3y2
(2)( 2x + 1 )( 3x2 - x – 5 )
= 6x3 - 2x2 – 10x + 3x2 – x - 5
= 6x3 + x2 - 11x - 5.
【例1】计算:
(1)( 2x + y )( x – 3y );
(2)( 2x + 1 )( 3x2 – x – 5 );
(3)( x + a )( x + b ).
(3) ( x + a )( x + b )
= x2 + bx + ax + ab
= x2 + ( a + b )x + ab
第(3)小题的直观意义如图
【例1】计算:
(1)( 2x + y )( x – 3y );
(2)( 2x + 1 )( 3x2 – x – 5 );
(3)( x + a )( x + b ).
1、计算:
(1) (1-x)(0.6-x);(2) (2x+y)(x-y);(3) (x + y)(x2-xy + y2).
解:(1) 原式 = 1×0.6-1×x-x · 0.6 + x · x
= 0.6-x-0.6x + x2
= 0.6-1.6x + x2.
(2) 原式 = 2x·x-2x · y + y · x- y · y
= 2x2-2xy + xy-y2
= 2x2-xy-y2.
解:原式 = x · x2-x · xy + xy2 + x2y-xy2 + y · y2
= x3-x2y + xy2 + x2y-xy2 + y3
= x3 + y3.
注意:(1) 漏乘;(2) 符号问题;(3) 最后结果应
化成最简形式 (是同类项的要合并).
(3) (x + y)(x2-xy + y2).
【例2】计算:(1)( a+b )( a-b );
(2)( a+b )2;
(3)( a-b )2.
解:(1)( a+b )( a-b )=a2-ab+ba-b2=a2-b2.
(2)( a+b )2=( a+b )( a-b )=a2+ab+ba+b2=a2+2ab+b2.
(3)( a-b )2=( a-b )( a-b )=a2-ab-ba+b2.
2、先化简,再求值:(a-2b)(a2+2ab+4b2)-a(a-5b)(a+3b),其中 a=-1,b=1.
解:原式=a3-8b3-(a2-5ab)(a+3b)
=a3-8b3-a3-3a2b+5a2b+15ab2
=-8b3+2a2b+15ab2.
当 a=-1,b=1 时,原式=-8+2-15=-21.
方法总结:化简求值的题型,一般应先化简,再
求值,而不是先代值,再计算.
1. 下列计算对不对? 如果不对, 应怎样改正?
(1)( 3a-b )( 2a + b ) = 3a·2a + ( - b )·b = 6a2- b2;
(2) ( x + 3 ) ( 1 - x ) = x·1 + x·x + 3 - 3·x = x2 - 2x + 3 .
解:(1)不对,应为 ( 3a-b )( 2a + b ) = 3a·2a + 3a·b - b ·2a - b ·b = 6a2 + ab - b2 ;
(2)不对,应为 ( x + 3 ) ( 1 - x )= x·1- x·x + 3×1-3·x = x - x2 + 3-3x = -x2-2x + 3
2.判断下列解法是否正确,若不正确请说出理由.
解:原式
解:原式
3. 计算:
(1)(x-2)(x+3);
(2)(x+1)(x+5);
(3)(x+4)(x-5);
(4)(x-3)2;
= x2+x-6
= x2+6x+5
= x2-x-20
= x2-6x+9.
(5)(x+2y)2;
(6)(m-2n)(2m+n);
(7)(3a+2b)(3a-2b);
(8)(3a-2b)2.
= x2+4xy+4y2
= 2m2-3mn-2n2
= 9a2-4b2
= 9a2-12ab+4b2.
4. 计算:
(1)( x-2 )( x + 3 ) ;(2) ( x + 1 ) ( x + 5 ) ;
(3)( x + 4 )( x - 5 );(4)( x - 3 )2.
解:(1)( x-2 )( x + 3 ) = x2 +3x-2x-6 = x2 + x-6;
(2) ( x + 1 ) ( x + 5 ) = x2 + 6x + 5;
(3)( x + 4 )( x - 5 )= x2-5x + 4x-20 = x2-x-20
(4)( x - 3 )2 = ( x - 3 ) ( x - 3 ) = x2-3x+9 = x2-6x+9
5.计算:(1) (x 3y)(x + 7y); (2) (2x + 5y)(3x 2y).
= x2 + 4xy 21y2.
解:(1) 原式 = x2 + 7xy 3yx 21y2
(2) 原式 = 2x 3x 2x 2y + 5 y 3x 5y 2y
= 6x2 4xy + 15xy 10y2
= 6x2 + 11xy 10y2.
6. 计算:
(1)( x + 2y )2 ; (2) ( m – 2n ) ( 2m + n ) ;
(3)( 3a + 2b )( 3a – 2b ); (4)( 3a – 2b )2.
解:(1)(x+2y)2= (x+2y) (x+2y)=x2+2xy+2xy+4y2=x2+4xy+4y2;
(2) (m–2n) (2m+n)=2m2+mn-4mn-2n2=2m2-3mn-2n2
(3)( 3a + 2b )( 3a – 2b )=9a2-4b2
(4)( 3a – 2b )2 = (3a–2b) (3a–2b ) = 9a2-6ab-6ab+4b2 = 9a2-12ab+4b2
7. 化简求值:(4x + 3y)(4x-3y) + (2x + y)(3x-5y),其中 x = 1,y =-2.
解:原式 =
当 x = 1,y = -2 时,
原式 = 22×12-7×1×(-2)-14×(-2)2
= 22 + 14-56 = -20.
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式中的每一项,再把所得的积相加.
注意:
(1)多项式与多项式相乘的结果仍是多项式;
(2)结果的项数应该是原两个多项式项数的积(没有合并同类 项之前),检验项数常常作为检验解题过程是否的有效方法.
(3)多项式与多项式相乘的结果中,要把同类项合并;
多项式乘法法则:
1. 习题2.1中第8、9、10、11题.
2.完成同步练习册中本课时的练习.
