3.3圆周角和圆心角的关系(2)(河南省郑州市)
文档属性
| 名称 | 3.3圆周角和圆心角的关系(2)(河南省郑州市) |  | |
| 格式 | rar | ||
| 文件大小 | 194.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-02-25 20:53:00 | ||
图片预览



文档简介
课件18张PPT。九年级数学(下)第三章 3.3(2)圆周角和圆心角的关系
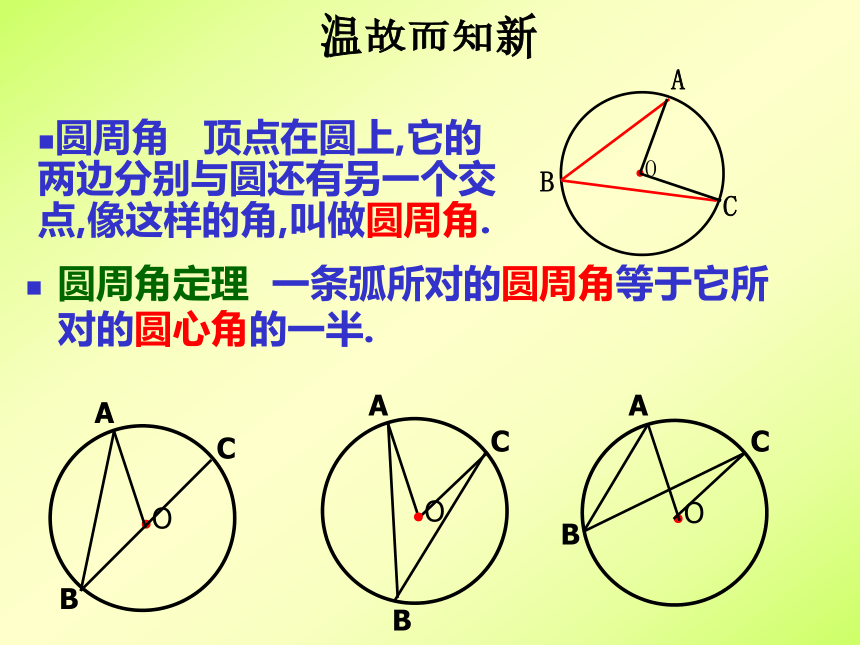
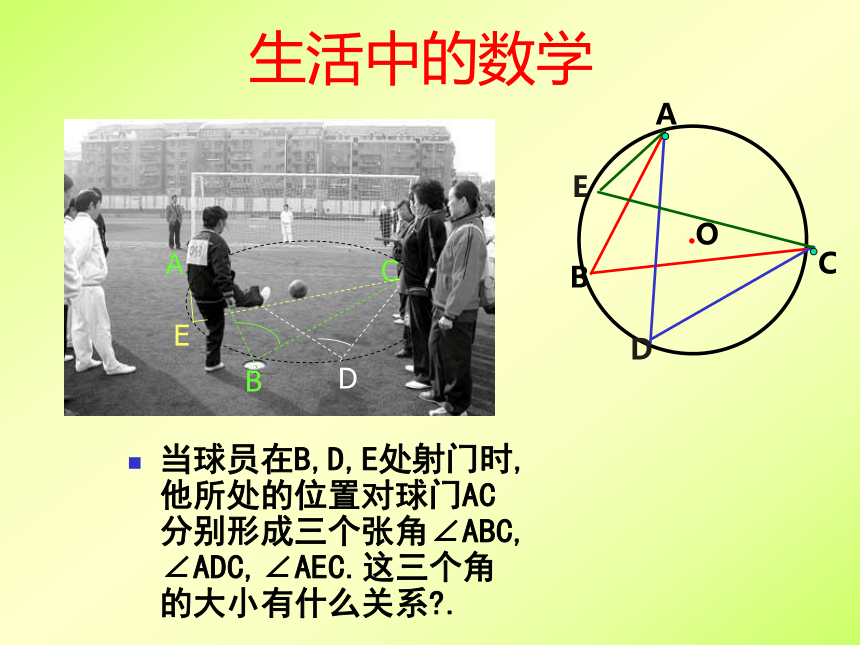
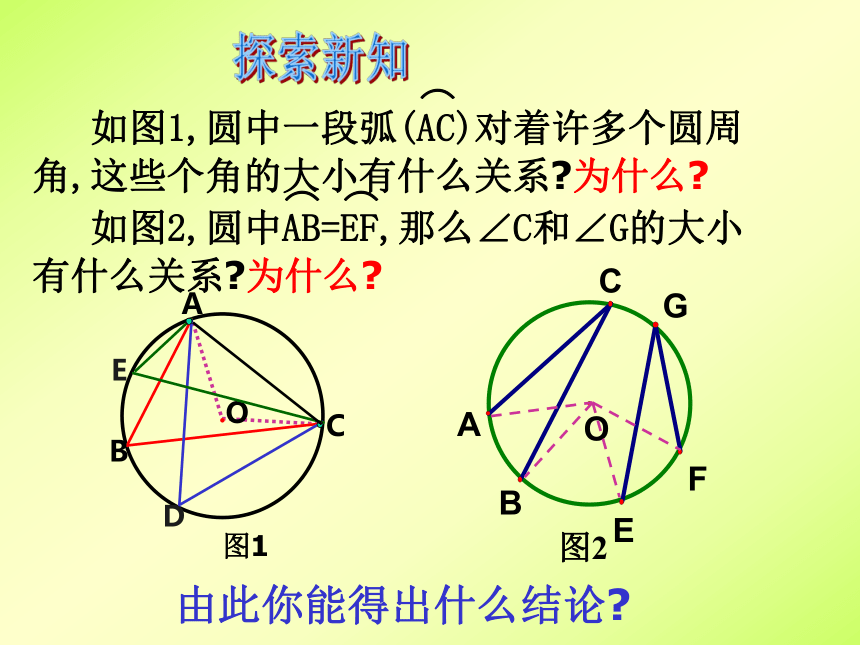
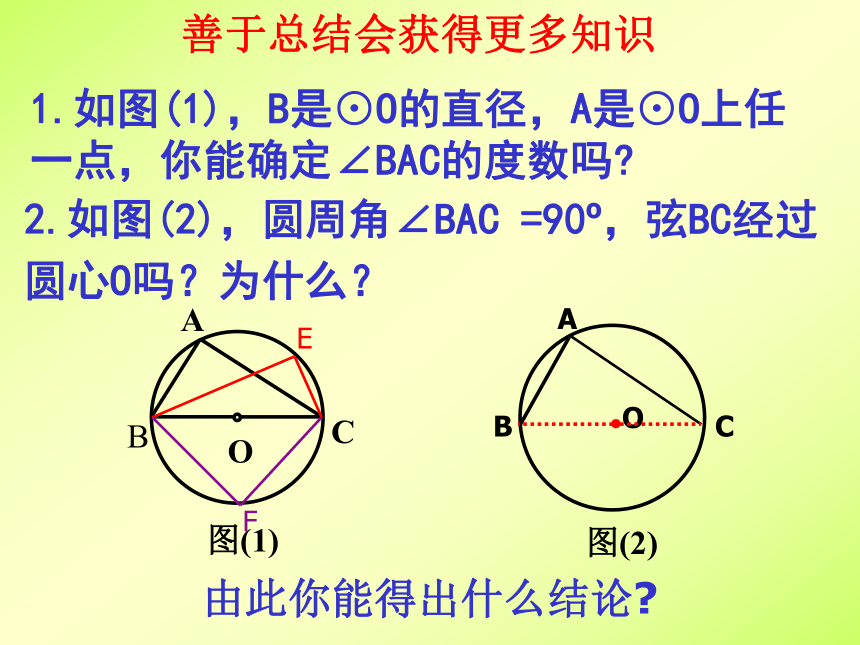
金水四中 徐天保圆周角 顶点在圆上,它的两边分别与圆还有另一个交点,像这样的角,叫做圆周角.圆周角定理 一条弧所对的圆周角等于它所对的圆心角的一半.温故而知新当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?.C生活中的数学由此你能得出什么结论?探索新知圆周角定理的推论1:同圆或等圆中,同弧或等弧所对的圆周角相等; 用于找相等的角1.如图(1),B是⊙O的直径,A是⊙O上任一点,你能确定∠BAC的度数吗?2.如图(2),圆周角∠BAC =90o,弦BC经过圆心O吗?为什么?由此你能得出什么结论?善于总结会获得更多知识用于判断某条弦是否是直径用于构造直角圆周角定理的推论2:半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径。圆周角定理的推论:推论1 同圆或等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.推论2 半圆(或直径)所对的圆周角是直角; 90°的圆周角所对的弦是直径. 1.如图,AB是⊙O的直径,BD是弦,延长BD到C,使AC=AB,CD与BD的大小有什么关系?为什么?知识应用解 BD=CD连接AD理由是:做一做船在航行过程中,船长常通过测定角度来确定是否
会遇到暗礁。如图,A,B表示灯塔,暗礁分布在经过
A,B两点的一个圆形区域内,C表示一个危险临界点,
∠ACB就是危险角,当船与两灯塔的夹角大于危险角时,
就有可能触礁。(1)当船与两灯塔的夹角大于危险角时,
船在哪个区域?为什么?(2)当船与两灯塔的夹角小于危险角时,
船在哪个区域?为什么?ABCEP·O温情提示 船与两灯塔的夹角大于危险角时,
船在圆形区域 边缘上。连接BE,∠AEB=危险角课堂练习1.判断题:
(1)等弧所对的圆周角相等. ( )
(2)相等的圆周角所对的弧也相等.( )
(3)90°的角所对的弦是直径. ( )
(4)同弦所对的圆周角相等. ( )
√XXX2.填空题:
(1)如图所示,
∠BAC= ,∠DAC= .∠DBC∠BDC(2)如图所示,⊙O的直径AB=10cm,
C为⊙O上一点,∠BAC=30°,
则BC= cm 53.如图,△ABC的顶点均在⊙O上,
AB=4, ∠C=30°,求⊙O的直径. E 如图,以⊙O的半径OA为直径作⊙O1,
⊙O的弦AD交⊙O1于C,则
(1)OC与AD的位置关系是_____ ;
(2)OC与BD的位置关系是_____ ;
(3)若OC = 2cm,则BD = __ cm。OC垂直平分AD平 行4知识深化C1、本节课我们学习了哪些知识?
小结圆周角定理的两个推论引辅助线的方法:
(1)构造直径上的圆周角。
(2)构造同弧所对的圆周角。2、本节课我们学习了哪些方法?1、已知顶角∠A=500的等腰三角形ABC内接于O,D是O上一点,
则∠ADB的度数是( )
A. 500 B. 650
C. 500或650 D. 650或1150思考题 .课本P109习题3.5 1,2题
金水四中 徐天保圆周角 顶点在圆上,它的两边分别与圆还有另一个交点,像这样的角,叫做圆周角.圆周角定理 一条弧所对的圆周角等于它所对的圆心角的一半.温故而知新当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?.C生活中的数学由此你能得出什么结论?探索新知圆周角定理的推论1:同圆或等圆中,同弧或等弧所对的圆周角相等; 用于找相等的角1.如图(1),B是⊙O的直径,A是⊙O上任一点,你能确定∠BAC的度数吗?2.如图(2),圆周角∠BAC =90o,弦BC经过圆心O吗?为什么?由此你能得出什么结论?善于总结会获得更多知识用于判断某条弦是否是直径用于构造直角圆周角定理的推论2:半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径。圆周角定理的推论:推论1 同圆或等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.推论2 半圆(或直径)所对的圆周角是直角; 90°的圆周角所对的弦是直径. 1.如图,AB是⊙O的直径,BD是弦,延长BD到C,使AC=AB,CD与BD的大小有什么关系?为什么?知识应用解 BD=CD连接AD理由是:做一做船在航行过程中,船长常通过测定角度来确定是否
会遇到暗礁。如图,A,B表示灯塔,暗礁分布在经过
A,B两点的一个圆形区域内,C表示一个危险临界点,
∠ACB就是危险角,当船与两灯塔的夹角大于危险角时,
就有可能触礁。(1)当船与两灯塔的夹角大于危险角时,
船在哪个区域?为什么?(2)当船与两灯塔的夹角小于危险角时,
船在哪个区域?为什么?ABCEP·O温情提示 船与两灯塔的夹角大于危险角时,
船在圆形区域 边缘上。连接BE,∠AEB=危险角课堂练习1.判断题:
(1)等弧所对的圆周角相等. ( )
(2)相等的圆周角所对的弧也相等.( )
(3)90°的角所对的弦是直径. ( )
(4)同弦所对的圆周角相等. ( )
√XXX2.填空题:
(1)如图所示,
∠BAC= ,∠DAC= .∠DBC∠BDC(2)如图所示,⊙O的直径AB=10cm,
C为⊙O上一点,∠BAC=30°,
则BC= cm 53.如图,△ABC的顶点均在⊙O上,
AB=4, ∠C=30°,求⊙O的直径. E 如图,以⊙O的半径OA为直径作⊙O1,
⊙O的弦AD交⊙O1于C,则
(1)OC与AD的位置关系是_____ ;
(2)OC与BD的位置关系是_____ ;
(3)若OC = 2cm,则BD = __ cm。OC垂直平分AD平 行4知识深化C1、本节课我们学习了哪些知识?
小结圆周角定理的两个推论引辅助线的方法:
(1)构造直径上的圆周角。
(2)构造同弧所对的圆周角。2、本节课我们学习了哪些方法?1、已知顶角∠A=500的等腰三角形ABC内接于O,D是O上一点,
则∠ADB的度数是( )
A. 500 B. 650
C. 500或650 D. 650或1150思考题 .课本P109习题3.5 1,2题
