湖南省长沙市重点中学2023-2024学年高一上学期期末考试数学试卷(PDF版含答案)
文档属性
| 名称 | 湖南省长沙市重点中学2023-2024学年高一上学期期末考试数学试卷(PDF版含答案) | 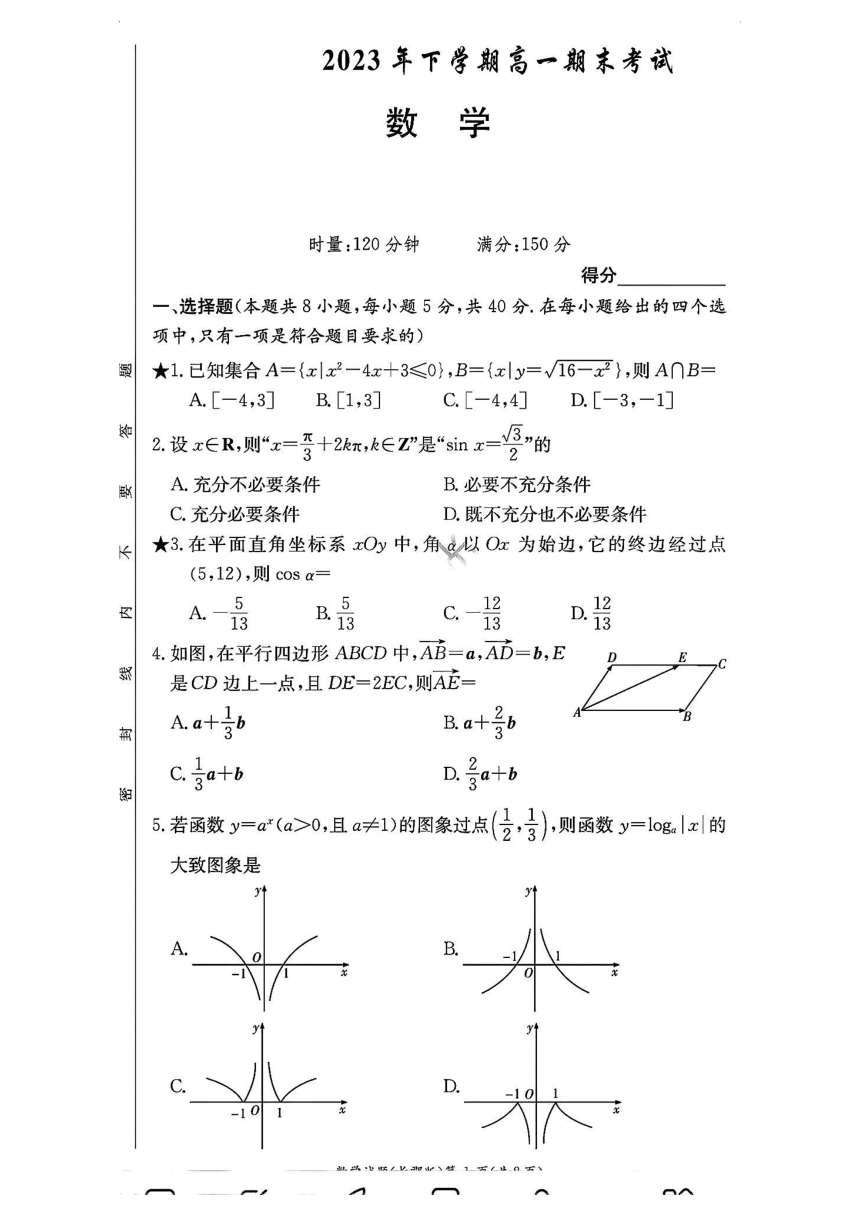 | |
| 格式 | |||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-28 08:02:15 | ||
图片预览





文档简介
2023年下学期高一期未考试
数学
时量:120分钟
满分:150分
得分
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选
项中,只有一项是符合题目要求的)
★1.已知集合A={x|x2-4x+3≤0},B={x|y=√16-x2},则A∩B=
A.[-4,3]
B.[1,3]
C.C-4,4]
D.[-3,-1]
铷
2.设x∈R,则“z=答+2kr,k∈Z是“sinc=9”的
2
敏
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
长
★3.在平面直角坐标系xOy中,角心以Ox为始边,它的终边经过点
(5,12),则c0sa=
K
A是
&品
c号
n号
4.如图,在平行四边形ABCD中,AB=a,AD=b,E
是CD边上一点,且DE=2EC,则AE=
A.argb
8a+导b
Cgatb
粗
D.是a+b
5.若函数y=c(a>0,且a≠1)的图象过点(分,),则函数y=-1og.Ixl的
大致图象是
6.已知f(x)=m(x-2)(x+m+3),g(x)=3x-3,若命题“Vx∈R,
f(x)<0或g(x)<0”为真命题,则m的取值范围是
A(-4,》
B.(-4,0)
c(o,)
D.(0,十∞)
7.已知定义在(0,十∞)上的f(x)是单调函数,且对任意x∈(0,十∞)恒
有f(f(x)十logx)=4,则函数f(x)的零点为
A京
B司
C.9
D.27
8.若a∈[-受,受且sine=x,则可以记a=arcsin;若a∈[0,元]且cosa
=x,则可以记a=arccos x.实数y∈(0,l),且(arccos y)2一(arcsin y)2
=a,则2y2-1=
A.cos(2)
B.-sim(2a)Ccos(e)
D.一sin(g)
二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,
有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得
0分)
9.已知关于x的不等式ax2十bx十c≥0的解集为{xx<一3,或x>2},则
A.a>0
B.不等式bx十c>0的解集是{xx<一6}
C.a+b+c>0
D.不等式cr2-bx十a<0的解集是{zx<-,或x>}
10.设正实数a,b满足a十b=1,则
Aab≥
B.√a+√b≤V2
ca2+≥司
D+≥
11.已知函数f(x)=3sin(2x十),函数g(x)的图象由f(x)图象向右平
移牙个单位长度得到,则下列关于函数g(x)的说法正确的有
Ag(x)的图象关于点(臣,0)对称
B.g(x)的图象关于直线x=5对称
Cg(x)在[-无,]上单调通增
D.g(x)在-石,]上单调递诚
数学
时量:120分钟
满分:150分
得分
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选
项中,只有一项是符合题目要求的)
★1.已知集合A={x|x2-4x+3≤0},B={x|y=√16-x2},则A∩B=
A.[-4,3]
B.[1,3]
C.C-4,4]
D.[-3,-1]
铷
2.设x∈R,则“z=答+2kr,k∈Z是“sinc=9”的
2
敏
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
长
★3.在平面直角坐标系xOy中,角心以Ox为始边,它的终边经过点
(5,12),则c0sa=
K
A是
&品
c号
n号
4.如图,在平行四边形ABCD中,AB=a,AD=b,E
是CD边上一点,且DE=2EC,则AE=
A.argb
8a+导b
Cgatb
粗
D.是a+b
5.若函数y=c(a>0,且a≠1)的图象过点(分,),则函数y=-1og.Ixl的
大致图象是
6.已知f(x)=m(x-2)(x+m+3),g(x)=3x-3,若命题“Vx∈R,
f(x)<0或g(x)<0”为真命题,则m的取值范围是
A(-4,》
B.(-4,0)
c(o,)
D.(0,十∞)
7.已知定义在(0,十∞)上的f(x)是单调函数,且对任意x∈(0,十∞)恒
有f(f(x)十logx)=4,则函数f(x)的零点为
A京
B司
C.9
D.27
8.若a∈[-受,受且sine=x,则可以记a=arcsin;若a∈[0,元]且cosa
=x,则可以记a=arccos x.实数y∈(0,l),且(arccos y)2一(arcsin y)2
=a,则2y2-1=
A.cos(2)
B.-sim(2a)Ccos(e)
D.一sin(g)
二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,
有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得
0分)
9.已知关于x的不等式ax2十bx十c≥0的解集为{xx<一3,或x>2},则
A.a>0
B.不等式bx十c>0的解集是{xx<一6}
C.a+b+c>0
D.不等式cr2-bx十a<0的解集是{zx<-,或x>}
10.设正实数a,b满足a十b=1,则
Aab≥
B.√a+√b≤V2
ca2+≥司
D+≥
11.已知函数f(x)=3sin(2x十),函数g(x)的图象由f(x)图象向右平
移牙个单位长度得到,则下列关于函数g(x)的说法正确的有
Ag(x)的图象关于点(臣,0)对称
B.g(x)的图象关于直线x=5对称
Cg(x)在[-无,]上单调通增
D.g(x)在-石,]上单调递诚
同课章节目录
