数学人教A版(2019)必修第一册3.2.1最大(小)值 课件(共16张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册3.2.1最大(小)值 课件(共16张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-28 08:46:11 | ||
图片预览




文档简介
(共16张PPT)
人教A版2019必修第一册
第 3章 函数的概念与性质
3.2.1 单调性与最大(小)值—最值(第2课时)
学习目标
1.理解函数的最大值和最小值的概念及其几何意义.(数学抽象)
2.能借助函数的图象和单调性,求一些简单函数的最值.(数学运算)
3.能利用函数的最值解决有关的实际应用问题.(数学建模)
提出问题,导入新课
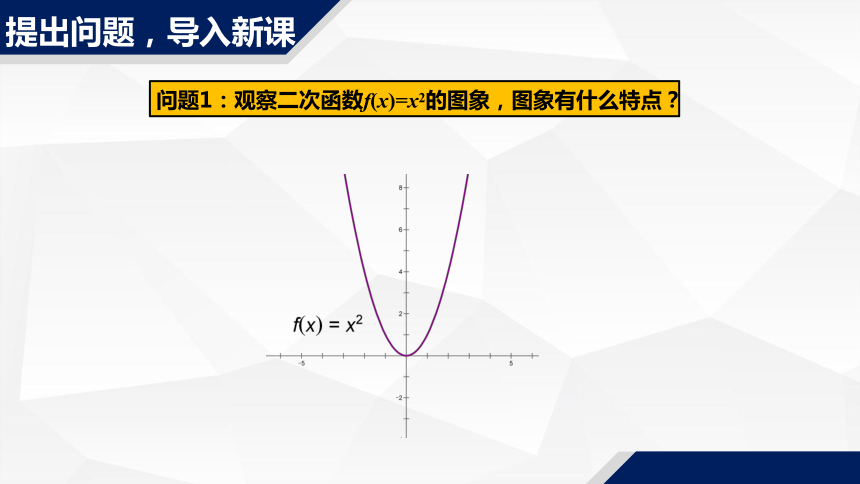
问题1:观察二次函数f(x)=x2的图象,图象有什么特点?
提出问题,导入新课
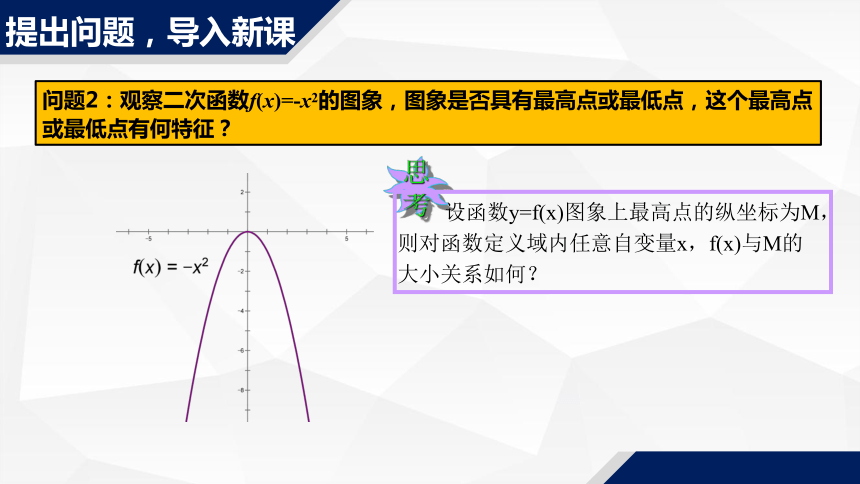
问题2:观察二次函数f(x)=-x2的图象,图象是否具有最高点或最低点,这个最高点或最低点有何特征?
思考
设函数y=f(x)图象上最高点的纵坐标为M,
则对函数定义域内任意自变量x,f(x)与M的大小关系如何?
提出问题,导入新课
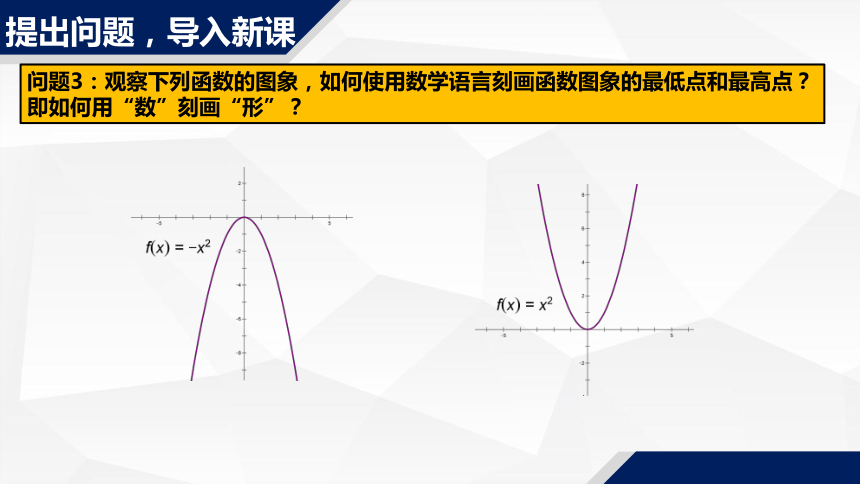
问题3:观察下列函数的图象,如何使用数学语言刻画函数图象的最低点和最高点?即如何用“数”刻画“形”?
师生互动,探索新知
问题4:你能仿照函数最大值的定义,给出函数y=f(x)的最小值的定义吗?
函数 最大值 最小值
条件 设函数y=f(x)的定义域为D,若存在实数M满足: x∈D,都有f(x)≤M; x0∈D,使得f(x0)=M.
结论 称M是函数y=f(x)的最大值 称M是函数y=f(x)的最小值
几何意义 f(x)图象上最高点的纵坐标
x∈D,都有f(x)≥M;
x0∈D,使得f(x0)=M.
最大(小)值必须是一个确定的函数值,且为值域中的一个元素.
f(x)图象上最低点的纵坐标
思考:一个函数一定有最大值或最小值吗?为什么?
学以致用,巩固新知
例1 “菊花”烟花是最壮观的烟花之一.制造时一般是期望它在达到最高点时爆裂.如果烟花距地面的高度h(单位:m) 与时间t(单位:s)之间的关系为 h(t)=-4.9t2+14.7t+18 ,那么烟花冲出后什么时刻爆裂是最佳时刻?这时离地面的高度是多少(精确到1 m)?
解:画出函数h(t)=-4.9t2+14.7t+18的图象.
函数图象的顶点就是烟花上升的最高点,顶点的横坐标就是烟花爆裂的最佳时刻,纵坐标就是这时距地面的高度.
由二次函数的知识可知,对于h(t)=-4.9t2+14.7t+18有:
∴烟花冲出后1.5秒是它爆裂的最佳时刻,这时距地面的高度为29 m.
图象法求函数最值
跟踪训练:
例2.已知函数 ,求这个函数的最大值和最小值。
解:设x1,x2是区间[2,6]上的任意两个实数,且x1所以,函数 在区间[2,6]上单调递减.
因此,函数 在区间[2,6]上的最大值为 ,最小值为
利用单调性求最值
利用单调性求最值
跟踪训练:
归纳小结 提升认识
1.函数最大值、最小值的概念;
2.利用图象、单调性求最大值、最小值的方法.
随堂检测
1.函数y=x+的值域是( )
A.[0,+∞) B.[2,+∞)
C.[4,+∞) D.[,+∞)
解析:B 函数y=x+在[2,+∞)上是增函数,所以其最小值为2,其值域为[2,+∞).
2.函数y=的最大值是( )
A.3 B.4
C.5 D.6
解析:C 当x<1时,函数y=x+3单调递增,有y<4,无最大值;当x≥1时,函数y=-x+6单调递减,在x=1处取得最大值5.所以该函数的最大值为5.
3.若函数y=ax+1在[1,2]上的最大值与最小值的差为2,则实数a的值为 .
解析:由题意知a≠0,当a>0时,有(2a+1)-(a+1)=2,解得a=2;当a<0时,有(a+1)-(2a+1)=2,解得a=-2,综上知a=±2.
答案:±2
4.用长度为24 m的材料围一矩形场地,中间加两道隔墙,要使矩形的面积最大,则隔墙的长度为 m.
解析:设隔墙长度为x m,场地面积为S m2,则S=x·=12x-2x2=-2(x-3)2+18.所以当x=3时,S有最大值.
答案:3
谢谢学习
停顿
人教A版2019必修第一册
第 3章 函数的概念与性质
3.2.1 单调性与最大(小)值—最值(第2课时)
学习目标
1.理解函数的最大值和最小值的概念及其几何意义.(数学抽象)
2.能借助函数的图象和单调性,求一些简单函数的最值.(数学运算)
3.能利用函数的最值解决有关的实际应用问题.(数学建模)
提出问题,导入新课
问题1:观察二次函数f(x)=x2的图象,图象有什么特点?
提出问题,导入新课
问题2:观察二次函数f(x)=-x2的图象,图象是否具有最高点或最低点,这个最高点或最低点有何特征?
思考
设函数y=f(x)图象上最高点的纵坐标为M,
则对函数定义域内任意自变量x,f(x)与M的大小关系如何?
提出问题,导入新课
问题3:观察下列函数的图象,如何使用数学语言刻画函数图象的最低点和最高点?即如何用“数”刻画“形”?
师生互动,探索新知
问题4:你能仿照函数最大值的定义,给出函数y=f(x)的最小值的定义吗?
函数 最大值 最小值
条件 设函数y=f(x)的定义域为D,若存在实数M满足: x∈D,都有f(x)≤M; x0∈D,使得f(x0)=M.
结论 称M是函数y=f(x)的最大值 称M是函数y=f(x)的最小值
几何意义 f(x)图象上最高点的纵坐标
x∈D,都有f(x)≥M;
x0∈D,使得f(x0)=M.
最大(小)值必须是一个确定的函数值,且为值域中的一个元素.
f(x)图象上最低点的纵坐标
思考:一个函数一定有最大值或最小值吗?为什么?
学以致用,巩固新知
例1 “菊花”烟花是最壮观的烟花之一.制造时一般是期望它在达到最高点时爆裂.如果烟花距地面的高度h(单位:m) 与时间t(单位:s)之间的关系为 h(t)=-4.9t2+14.7t+18 ,那么烟花冲出后什么时刻爆裂是最佳时刻?这时离地面的高度是多少(精确到1 m)?
解:画出函数h(t)=-4.9t2+14.7t+18的图象.
函数图象的顶点就是烟花上升的最高点,顶点的横坐标就是烟花爆裂的最佳时刻,纵坐标就是这时距地面的高度.
由二次函数的知识可知,对于h(t)=-4.9t2+14.7t+18有:
∴烟花冲出后1.5秒是它爆裂的最佳时刻,这时距地面的高度为29 m.
图象法求函数最值
跟踪训练:
例2.已知函数 ,求这个函数的最大值和最小值。
解:设x1,x2是区间[2,6]上的任意两个实数,且x1
因此,函数 在区间[2,6]上的最大值为 ,最小值为
利用单调性求最值
利用单调性求最值
跟踪训练:
归纳小结 提升认识
1.函数最大值、最小值的概念;
2.利用图象、单调性求最大值、最小值的方法.
随堂检测
1.函数y=x+的值域是( )
A.[0,+∞) B.[2,+∞)
C.[4,+∞) D.[,+∞)
解析:B 函数y=x+在[2,+∞)上是增函数,所以其最小值为2,其值域为[2,+∞).
2.函数y=的最大值是( )
A.3 B.4
C.5 D.6
解析:C 当x<1时,函数y=x+3单调递增,有y<4,无最大值;当x≥1时,函数y=-x+6单调递减,在x=1处取得最大值5.所以该函数的最大值为5.
3.若函数y=ax+1在[1,2]上的最大值与最小值的差为2,则实数a的值为 .
解析:由题意知a≠0,当a>0时,有(2a+1)-(a+1)=2,解得a=2;当a<0时,有(a+1)-(2a+1)=2,解得a=-2,综上知a=±2.
答案:±2
4.用长度为24 m的材料围一矩形场地,中间加两道隔墙,要使矩形的面积最大,则隔墙的长度为 m.
解析:设隔墙长度为x m,场地面积为S m2,则S=x·=12x-2x2=-2(x-3)2+18.所以当x=3时,S有最大值.
答案:3
谢谢学习
停顿
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
