人教B版必修4第二章 平面向量2.3.3平面向量的坐标运算(
文档属性
| 名称 | 人教B版必修4第二章 平面向量2.3.3平面向量的坐标运算( |

|
|
| 格式 | rar | ||
| 文件大小 | 133.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-02-24 00:00:00 | ||
图片预览




文档简介
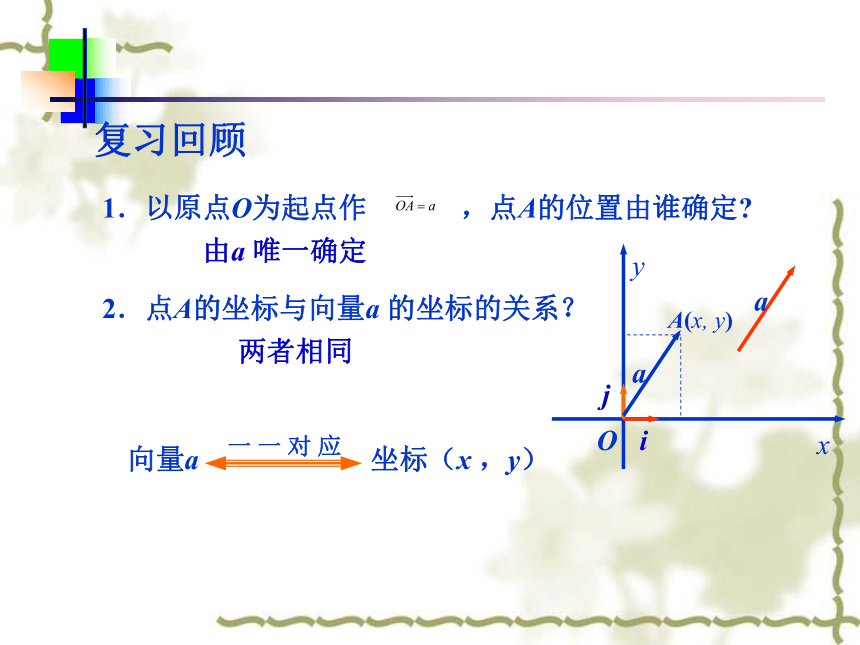
课件10张PPT。2.3 平面向量的坐标表示与运算由a 唯一确定2.点A的坐标与向量a 的坐标的关系?两者相同复习回顾已知 , ,猜一猜
的坐标表示。创设情境平面向量的坐标运算两个向量和与差的坐标分别等于这两向量相应坐标的和与差解: 一个向量的坐标等于表示此向量的有向线段的终点的坐
标减去始点的坐标. 实数与向量的积的坐标等于这个实数乘原来的向量的相
应坐标.合作探究,应用新知 例.已知 =(2,1), =(-3,4),求 ,
, 的坐标. =(2,1)-(-3,4)=(5,-3); =3(2,1)+4(-3,4)
=(6,3)+(-12,16)
=(-6,19) 例. 已知 ABCD的三个顶点A、B、C的坐标分别为
(-2,1)、( -1,3)、(3,4),求顶点D的坐标.解:设顶点D的坐标为(x,y)1.若M(3, -2) N(-5, -1) 且 , 求P点的坐标
2.若A(0, 1), B(1, 2), C(3, 4),则
= .
3.已知:四点A(5, 1), B(3, 4), C(1,3), D(5, -3) , 求证:四边形ABCD是梯形.反馈练习,巩固新知 ?2 归纳小结 1、通过本节课的学习,你收获了什么?
2、我们已经学习了利用图形来进行向量的运算,为什么还要引进坐标运算呢?布置作业 课本的习题:
思考题一:观察课本例二中的向量和 ,思考相反向量的坐标关系;
思考题二:对课本例五进行变式训练,将原题中的平行四边形ABCD的顺序去掉,思考点D可能的情况。变式以后问题的结论除了例三的情况外,还有另外两种情况。
的坐标表示。创设情境平面向量的坐标运算两个向量和与差的坐标分别等于这两向量相应坐标的和与差解: 一个向量的坐标等于表示此向量的有向线段的终点的坐
标减去始点的坐标. 实数与向量的积的坐标等于这个实数乘原来的向量的相
应坐标.合作探究,应用新知 例.已知 =(2,1), =(-3,4),求 ,
, 的坐标. =(2,1)-(-3,4)=(5,-3); =3(2,1)+4(-3,4)
=(6,3)+(-12,16)
=(-6,19) 例. 已知 ABCD的三个顶点A、B、C的坐标分别为
(-2,1)、( -1,3)、(3,4),求顶点D的坐标.解:设顶点D的坐标为(x,y)1.若M(3, -2) N(-5, -1) 且 , 求P点的坐标
2.若A(0, 1), B(1, 2), C(3, 4),则
= .
3.已知:四点A(5, 1), B(3, 4), C(1,3), D(5, -3) , 求证:四边形ABCD是梯形.反馈练习,巩固新知 ?2 归纳小结 1、通过本节课的学习,你收获了什么?
2、我们已经学习了利用图形来进行向量的运算,为什么还要引进坐标运算呢?布置作业 课本的习题:
思考题一:观察课本例二中的向量和 ,思考相反向量的坐标关系;
思考题二:对课本例五进行变式训练,将原题中的平行四边形ABCD的顺序去掉,思考点D可能的情况。变式以后问题的结论除了例三的情况外,还有另外两种情况。
