2023-2024学年第一学期甘肃省武威市凉州区八年级数学《全等三角形》基础专项训练(含答案)
文档属性
| 名称 | 2023-2024学年第一学期甘肃省武威市凉州区八年级数学《全等三角形》基础专项训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 336.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-29 18:21:37 | ||
图片预览



文档简介
2023-2024学年第一学期甘肃省武威市凉州区
八年级数学《全等三角形》基础专项训练
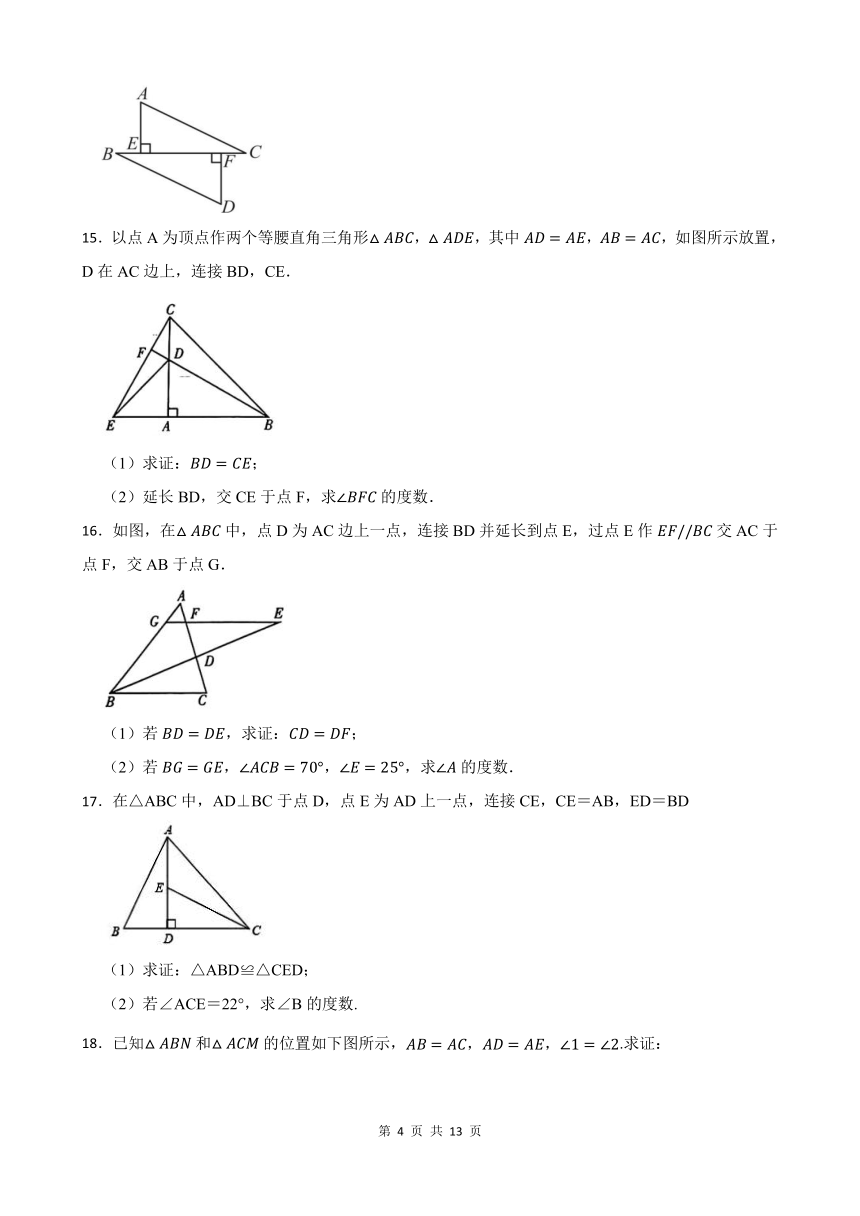
1.已知:如图,点在上,点在上,和相交于点,,求证:.
2.如图所示,已知点E、F、D在同一条直线上,AF=DE,AB⊥DC,CE⊥AD,垂足分别为F、E,AB=DC,求证:AB∥CD.
3.如图,已知,点B,E,C,F在同一条直线上.
(1)若,,求的度数;
(2)若,,求的长.
4.如图,A,B,C,D是同一条直线上的点,AC=BD,AE∥DF,∠1=∠2.求证:BE=CF.
5.如图,在四边形ABCD中,,,,点E是线段BD上一点,且.
(1)求证:;
(2)直接写出图中所有的等腰三角形.
6.如图,已知△BAC和△DAE的顶点A重合,∠BAC=∠DAE,AB=AC,AD=AE,连接BD、CE交于点M.
(1)证明:∠ABD=∠ACE;
(2)若∠BAC=70°,求∠BMC的大小.
7.如图,和中,,,,边与边交于点(不与、重合),点、在异侧;
(1)求证;
(2)若,,求的度数.
8.如图,已知点,,,在直线上,点,在异侧,且,.
(1)请你添加一个适当的条件:使得.结合所添加的条件证明;
(2)在(1)的条件下,若,,求的长度.
9.如图,,,.求证:.
10.如图,在△ABC中,D是边AB上一点,E是边AC的中点,作CF∥AB交DE的延长线于点F.
(1)证明:△ADE≌△CFE;
(2)若∠B=∠ACB,CE=5,CF=7,求DB.
11. 如图,,,,
(1)求证:≌.
(2)求证:
12.如图,四边形中,,,且点、分别是线段、的中点.求证:.
13.如图所示,在中,为的中点,,交的平分线于点,于点,交延长线于点.求证:.
14. 如图,点E,F在BC上,,,,.求证:.
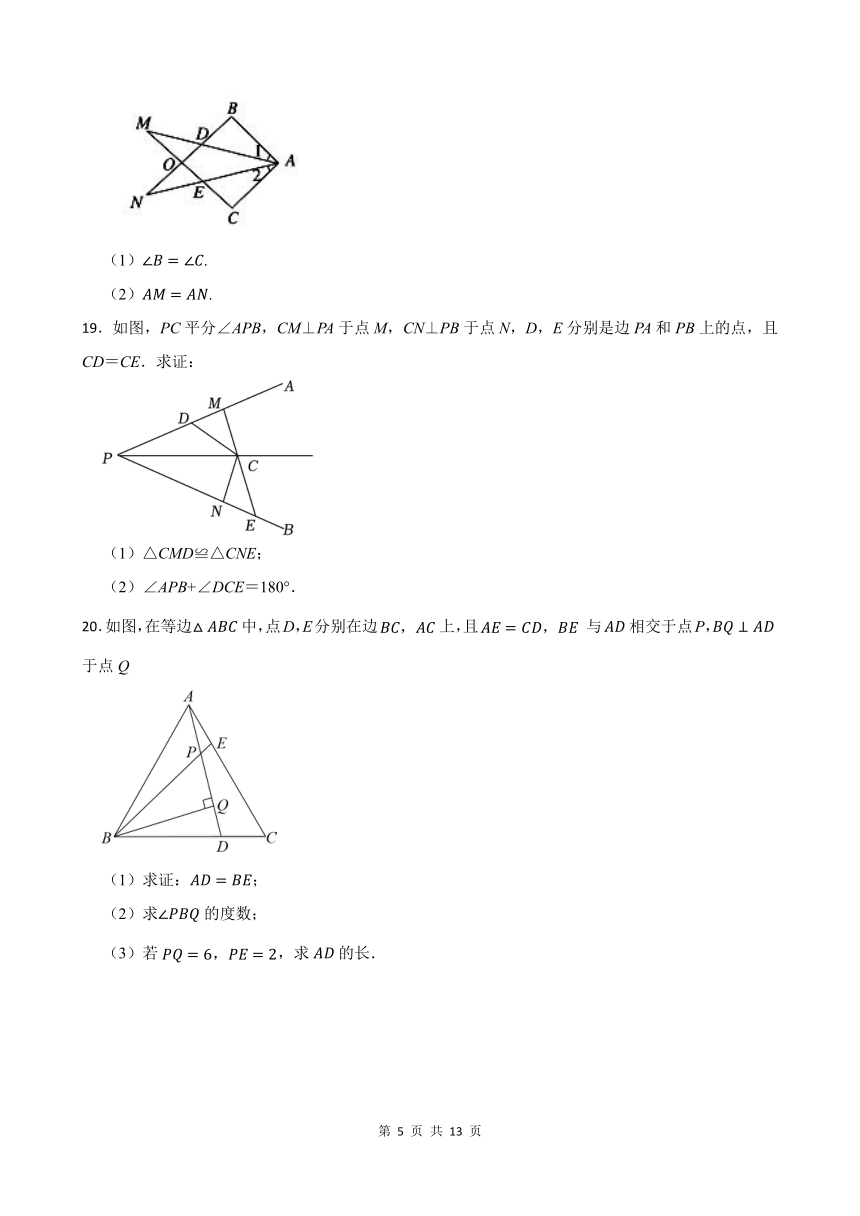
15.以点A为顶点作两个等腰直角三角形,,其中,,如图所示放置,D在AC边上,连接BD,CE.
(1)求证:;
(2)延长BD,交CE于点F,求的度数.
16.如图,在中,点D为AC边上一点,连接BD并延长到点E,过点E作交AC于点F,交AB于点G.
(1)若,求证:;
(2)若,,,求的度数.
17.在△ABC中,AD⊥BC于点D,点E为AD上一点,连接CE,CE=AB,ED=BD
(1)求证:△ABD≌△CED;
(2)若∠ACE=22°,求∠B的度数.
18.已知和的位置如下图所示,.求证:
(1).
(2).
19.如图,PC平分∠APB,CM⊥PA于点M,CN⊥PB于点N,D,E分别是边PA和PB上的点,且CD=CE.求证:
(1)△CMD≌△CNE;
(2)∠APB+∠DCE=180°.
20.如图,在等边中,点D,E分别在边上,且 与相交于点P,于点Q
(1)求证:;
(2)求的度数;
(3)若,求的长.
答案
1.证明:在和中,
∵,
∴,
∴,
∴,即
2.证明:∵BF⊥AD,CE⊥AD,
∴∠AFB=∠DEC=90°,
在Rt△AFB和Rt△DFC中,
∴Rt△AFB≌Rt△DEC(HL),
∴∠A=∠D,
∴AB∥CD.
3.(1)解:∵,,
∴.
∵,
∴;
(2)解:∵,,
∴
∵,
∴,
∴.
故答案为:7.
4.证明:
∵AC=AB+BC,BD=BC+CD,AC=BD,
∴AB=DC,
∵AE∥DF,
∴∠A=∠D,
在△ABE和△DCF中,
,
∴△ABE≌△DCF,
∴BE=CF.
5.(1)证明:∵,∴,∵,∴,
在和中,,
∴.
(2)、
6.(1)证明:∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE;
(2)解:∠BAC=∠DAE=70°.
设BD与AC交于点F,由(1)得∠ABD=∠ACE,
在△ABF和△CMF中,∠AFB=∠CFM,
∵∠ABD+∠AFB+∠BAC=180°,∠ACE+∠MFC+∠BMC=180°,
∴∠BMC=∠BAC=70°.
7.(1)证明:
2分
在和中,
(2)解:
由(1)知
8.(1)解:答对即可,添加的条件是
证明:
在和中:
(已证)
(2)解:,
9.解:∵,
∴,
即,
在和中,
,
∴
∴
10.(1)证明:∵E是边AC的中点,
∴AE=CE.
又∵CF∥AB,
∴∠A=∠ACF,∠ADF=∠F,
在△ADE与△CFE中,
∴△ADE≌△CFE(AAS).
(2)解:∵△ADE≌△CFE,CF=7,
∴CF=AD=7,
又∵∠B=∠ACB,
∴AB=AC,
∵E是边AC的中点,CE=3,
∴AC=2CE=10.
∴AB=10,
∴DB=AB-AD=10-7=4.
11.(1)证明:∵,∴,即,
在和中,,
≌(SSS).
(2)证明:∵≌,∴,
∴.
12.证明:∵点是的中点,
∴
在中,
,
∴,
∴,
∵点是的中点.
∴,
∴.
13.证明:连接、,
,为中点,
∴垂直平分,
,
,,且平分,
,
在和中,
,
,
.
14.解:证明:,
,即.
,
.
在和中,,
,
,
∴.
15.(1)解:∵,都是等腰直角三角形,
∴,,,
∴,∴
(2)解:∵,∴,
∵,∴,
∴,∴
16.(1)证明:∵,∴,在和中,,
∴,∴
(2)解:∵,∴,
由(1)知,,∴,
∴.
17.(1)∵AD⊥BC,∴∠ADB=∠CDE=90°,
在Rt△ADB与Rt△CDE中,
,∴Rt△ADB≌Rt△CDE(HL)
(2)∵Rt△ADB≌Rt△CDE,
∴AD=CD,∴△ADC是等腰直角三角形,
∴∠ACD=45°,∴∠ECD=∠ACD﹣∠ACE=45°﹣22°=23°,
∴∠CED=90°﹣23°=67°,∴∠B=∠CED=67°,
18.(1)证明:由条件得(SAS),∴∠B=∠C
(2)证明:∵∠1=∠2,
即
又
19.(1)证明:∵PC平分∠APB,CM⊥PA于M,CN⊥PB于N,
∴CM=CN,
在Rt△DCM与Rt△ECN中,
,
∴Rt△CMD≌Rt△CNE(HL);
(2)证明:由(1)知:Rt△DCM≌Rt△ECN(HL),
∴∠DCM=∠ECN,
∴∠MCN=∠MCD+∠DCN=∠ECN+∠DCN=∠DCE,
∵∠PMC+∠PNC+∠APB+∠MCN=90°+90°+∠APB+∠MCN=360°,
∴∠APB+∠MCN=180°,
∴∠APB+∠DCE=180°.
20.(1)证明:∵为等边三角形,
∴,
在与中,
∵,
∴,
∴.
(2)解:由(1)得:,
∴,
∴,
∴,
∵,
∴,
∴.
(3)解:∵,,,
∴,
∵,
∴,
∵,
∴.
八年级数学《全等三角形》基础专项训练
1.已知:如图,点在上,点在上,和相交于点,,求证:.
2.如图所示,已知点E、F、D在同一条直线上,AF=DE,AB⊥DC,CE⊥AD,垂足分别为F、E,AB=DC,求证:AB∥CD.
3.如图,已知,点B,E,C,F在同一条直线上.
(1)若,,求的度数;
(2)若,,求的长.
4.如图,A,B,C,D是同一条直线上的点,AC=BD,AE∥DF,∠1=∠2.求证:BE=CF.
5.如图,在四边形ABCD中,,,,点E是线段BD上一点,且.
(1)求证:;
(2)直接写出图中所有的等腰三角形.
6.如图,已知△BAC和△DAE的顶点A重合,∠BAC=∠DAE,AB=AC,AD=AE,连接BD、CE交于点M.
(1)证明:∠ABD=∠ACE;
(2)若∠BAC=70°,求∠BMC的大小.
7.如图,和中,,,,边与边交于点(不与、重合),点、在异侧;
(1)求证;
(2)若,,求的度数.
8.如图,已知点,,,在直线上,点,在异侧,且,.
(1)请你添加一个适当的条件:使得.结合所添加的条件证明;
(2)在(1)的条件下,若,,求的长度.
9.如图,,,.求证:.
10.如图,在△ABC中,D是边AB上一点,E是边AC的中点,作CF∥AB交DE的延长线于点F.
(1)证明:△ADE≌△CFE;
(2)若∠B=∠ACB,CE=5,CF=7,求DB.
11. 如图,,,,
(1)求证:≌.
(2)求证:
12.如图,四边形中,,,且点、分别是线段、的中点.求证:.
13.如图所示,在中,为的中点,,交的平分线于点,于点,交延长线于点.求证:.
14. 如图,点E,F在BC上,,,,.求证:.
15.以点A为顶点作两个等腰直角三角形,,其中,,如图所示放置,D在AC边上,连接BD,CE.
(1)求证:;
(2)延长BD,交CE于点F,求的度数.
16.如图,在中,点D为AC边上一点,连接BD并延长到点E,过点E作交AC于点F,交AB于点G.
(1)若,求证:;
(2)若,,,求的度数.
17.在△ABC中,AD⊥BC于点D,点E为AD上一点,连接CE,CE=AB,ED=BD
(1)求证:△ABD≌△CED;
(2)若∠ACE=22°,求∠B的度数.
18.已知和的位置如下图所示,.求证:
(1).
(2).
19.如图,PC平分∠APB,CM⊥PA于点M,CN⊥PB于点N,D,E分别是边PA和PB上的点,且CD=CE.求证:
(1)△CMD≌△CNE;
(2)∠APB+∠DCE=180°.
20.如图,在等边中,点D,E分别在边上,且 与相交于点P,于点Q
(1)求证:;
(2)求的度数;
(3)若,求的长.
答案
1.证明:在和中,
∵,
∴,
∴,
∴,即
2.证明:∵BF⊥AD,CE⊥AD,
∴∠AFB=∠DEC=90°,
在Rt△AFB和Rt△DFC中,
∴Rt△AFB≌Rt△DEC(HL),
∴∠A=∠D,
∴AB∥CD.
3.(1)解:∵,,
∴.
∵,
∴;
(2)解:∵,,
∴
∵,
∴,
∴.
故答案为:7.
4.证明:
∵AC=AB+BC,BD=BC+CD,AC=BD,
∴AB=DC,
∵AE∥DF,
∴∠A=∠D,
在△ABE和△DCF中,
,
∴△ABE≌△DCF,
∴BE=CF.
5.(1)证明:∵,∴,∵,∴,
在和中,,
∴.
(2)、
6.(1)证明:∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE;
(2)解:∠BAC=∠DAE=70°.
设BD与AC交于点F,由(1)得∠ABD=∠ACE,
在△ABF和△CMF中,∠AFB=∠CFM,
∵∠ABD+∠AFB+∠BAC=180°,∠ACE+∠MFC+∠BMC=180°,
∴∠BMC=∠BAC=70°.
7.(1)证明:
2分
在和中,
(2)解:
由(1)知
8.(1)解:答对即可,添加的条件是
证明:
在和中:
(已证)
(2)解:,
9.解:∵,
∴,
即,
在和中,
,
∴
∴
10.(1)证明:∵E是边AC的中点,
∴AE=CE.
又∵CF∥AB,
∴∠A=∠ACF,∠ADF=∠F,
在△ADE与△CFE中,
∴△ADE≌△CFE(AAS).
(2)解:∵△ADE≌△CFE,CF=7,
∴CF=AD=7,
又∵∠B=∠ACB,
∴AB=AC,
∵E是边AC的中点,CE=3,
∴AC=2CE=10.
∴AB=10,
∴DB=AB-AD=10-7=4.
11.(1)证明:∵,∴,即,
在和中,,
≌(SSS).
(2)证明:∵≌,∴,
∴.
12.证明:∵点是的中点,
∴
在中,
,
∴,
∴,
∵点是的中点.
∴,
∴.
13.证明:连接、,
,为中点,
∴垂直平分,
,
,,且平分,
,
在和中,
,
,
.
14.解:证明:,
,即.
,
.
在和中,,
,
,
∴.
15.(1)解:∵,都是等腰直角三角形,
∴,,,
∴,∴
(2)解:∵,∴,
∵,∴,
∴,∴
16.(1)证明:∵,∴,在和中,,
∴,∴
(2)解:∵,∴,
由(1)知,,∴,
∴.
17.(1)∵AD⊥BC,∴∠ADB=∠CDE=90°,
在Rt△ADB与Rt△CDE中,
,∴Rt△ADB≌Rt△CDE(HL)
(2)∵Rt△ADB≌Rt△CDE,
∴AD=CD,∴△ADC是等腰直角三角形,
∴∠ACD=45°,∴∠ECD=∠ACD﹣∠ACE=45°﹣22°=23°,
∴∠CED=90°﹣23°=67°,∴∠B=∠CED=67°,
18.(1)证明:由条件得(SAS),∴∠B=∠C
(2)证明:∵∠1=∠2,
即
又
19.(1)证明:∵PC平分∠APB,CM⊥PA于M,CN⊥PB于N,
∴CM=CN,
在Rt△DCM与Rt△ECN中,
,
∴Rt△CMD≌Rt△CNE(HL);
(2)证明:由(1)知:Rt△DCM≌Rt△ECN(HL),
∴∠DCM=∠ECN,
∴∠MCN=∠MCD+∠DCN=∠ECN+∠DCN=∠DCE,
∵∠PMC+∠PNC+∠APB+∠MCN=90°+90°+∠APB+∠MCN=360°,
∴∠APB+∠MCN=180°,
∴∠APB+∠DCE=180°.
20.(1)证明:∵为等边三角形,
∴,
在与中,
∵,
∴,
∴.
(2)解:由(1)得:,
∴,
∴,
∴,
∵,
∴,
∴.
(3)解:∵,,,
∴,
∵,
∴,
∵,
∴.
