人教版七年级数学下册第七章 平面直角坐标系全章同步培优练习(含解析)
文档属性
| 名称 | 人教版七年级数学下册第七章 平面直角坐标系全章同步培优练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-28 14:09:17 | ||
图片预览



文档简介
第七章 平面直角坐标系
中小学教育资源及组卷应用平台
7.1 平面直角坐标系
1.(点的坐标)已知x轴上的点P 到y轴的距离为3,则点 P 的坐标为 ( )
A.(3,0) B.(0,3)
C.(0,3)或(0,-3) D.(3,0)或( -3,0)
2.(象限及点的坐标特征)若点 P(m,1)在第二象限,则点 Q(-m,0)在 ( )
A. x轴正半轴上 B. x轴负半轴上
C. y轴正半轴上 D. y轴负半轴上
3. (点的坐标)点 P(3 +a,a+1)到x轴距离为3,则点 P到y轴的距离为 .
4.(象限及点的坐标特征)若点P(2x-1,x+3)在第二、第四象限的角平分线上,则点 P 到x轴的距离为 .
5.(平面直角坐标系,象限及点的坐标特征)已知P(a,b)为平面直角坐标系中的一点.
(1)当ab<0时,点P 处于什么位置
(2)当ab=0时,点P 处于什么位置
6.(有序数对)如图,点 A 用(3,1)表示,并在 A处放3 个胡萝卜,1 棵青菜;点 B 用(2,3)表示,并在 B 处放2 个胡萝下,3 棵青菜.
(1)用有序数对表示点 C,D,E,F,并分别说明各处放几个胡萝卜,几棵青菜;
(2)若一只兔子从点 A 到达点 B(顺着方格线走),有以下几条路线可以选择:①A→C→
D→B;②A→F→D→B;③A→F→E→B.帮可爱的兔子选一条路线,使它吃到的食物最多.
7.(求平面直角坐标系中的图形面积)如图,四边形ABCD所在的网格图中,每个小正方形的边长均为1个单位长度.
(1)建立以点 B 为原点,AB 边所在直线为x轴的平面直角坐标系;
(2)写出点 A,B,C,D 的坐标;
(3)求出四边形 ABCD 的面积.
7.2 坐标方法的简单应用
1. (点的平移)若将点(-4,b)沿x轴的正方向平移2个单位长度得到点(a+1,3),则a,b的值分别是 ( )
A. -3,3 B. -5,3 C. -3,1 D. -5,1
2. (用坐标表示位置)(2021 ·山西中考)如图是一片枫叶标本,其形状呈“掌状五裂型”,裂片具有少数突出的齿,将其放在平面直角坐标系中,表示叶片“顶部”A,B两点的坐标分别为( -2,2),(-3,0),则叶杆“底部”点 C的坐标为 .
3.(用坐标表示位置)中国象棋文化历史久远. 某校开展了以“纵横之间有智慧,攻防转换有乐趣”为主题的中国象棋文化节.如图所示是某次对弈的残局图,如果建立平面直角坐标系,使“帥”位于点(-1,-2),“馬”位于点(2,-2),那么“兵”在同一坐标系下的坐标是 .
4.(规律探究题)如图,动点P 从坐标原点(0,0)出发,以每秒一个单位长度的速度按图中箭头所示方向运动,第1 秒运动到点(1,0),第2 秒运动到点(1,1),第3 秒运动到点(0,1),第4 秒运动到点(0,2),……则第2 068 秒点 P 所在位置的坐标是 .
5. (用方向和距离表示地理位置)下图是小明家和学校所在地的简单地图,已知 OA =2k m,OB=3. 5k m,OP=4km,C 为 OP 的中点,回答下列问题:
(1)图中与小明家距离相同的地方有哪些
(2)请用方向与距离描述学校、商场、停车场相对于小明家的位置.
6.(图形的平移)如图所示,三角形ABC 中任意一点P(a,b)经平移后对应点. 2),将三角形ABC 作同样的平移得到三角形A B C ,求点 A ,B ,C 的坐标.
专项点睛2 在平面直角坐标系中求几何图形的面积
1. 如图,在平面直角坐标系中,已知点A(-1,5),B(-1,0),C(-4,3),则三角形 ABC 的面积为 .
2. 如图所示,在平面直角坐标系中有A,B,C,D四个点,求出四边形ABCD的面积.
3. 如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中 a,b,c满足关系式
(1)求a,b,c的值;
(2)如果在第二象限内有一点 请用含 m 的式子表示四边形 ABOP 的面积;
(3)在(2)的条件下,是否存在点 P,使四边形
ABOP 的面积与三角形ABC 的面积相等 若存在,求出点 P 的坐标;若不存在,请说明理由.
4. 如图所示,已知A(0,1),B(2,0),C(4,3).
(1)求 的面积;
(2)设点 P 在坐标轴上,且 与 的面积相等,求点 P 的坐标.
第七章 培优精练
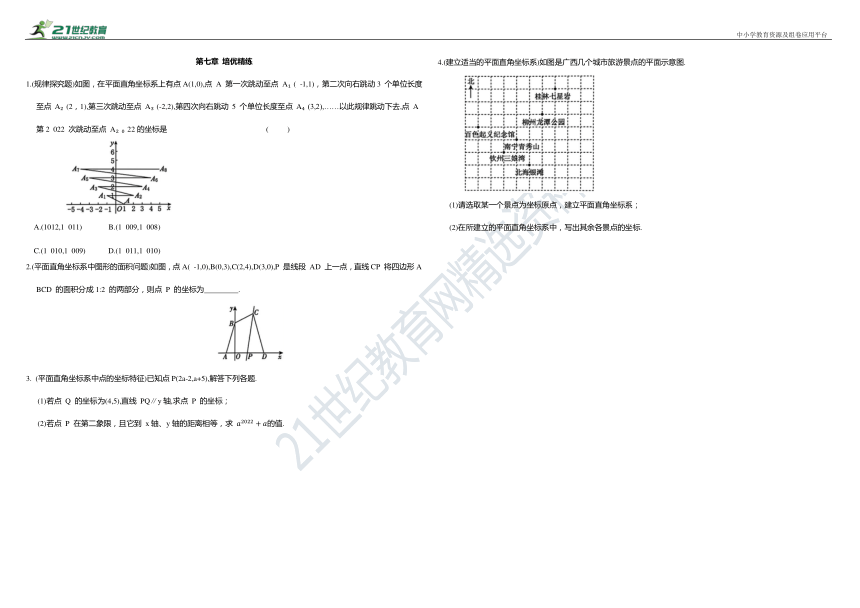
1.(规律探究题)如图,在平面直角坐标系上有点A(1,0),点 A 第一次跳动至点 A ( -1,1),第二次向右跳动3 个单位长度至点A (2,1),第三次跳动至点 A (-2,2),第四次向右跳动5 个单位长度至点A (3,2),……以此规律跳动下去,点 A 第2 022 次跳动至点 A 22的坐标是 ( )
A.(1012,1 011) B.(1 009,1 008)
C.(1 010,1 009) D.(1 011,1 010)
2.(平面直角坐标系中图形的面积问题)如图,点A( -1,0),B(0,3),C(2,4),D(3,0),P 是线段 AD 上一点,直线CP 将四边形ABCD 的面积分成1:2 的两部分,则点 P 的坐标为 .
3. (平面直角坐标系中点的坐标特征)已知点P(2a-2,a+5),解答下列各题.
(1)若点 Q 的坐标为(4,5),直线 PQ∥y轴,求点 P 的坐标;
(2)若点 P 在第二象限,且它到 x轴、y轴的距离相等,求 的值.
4.(建立适当的平面直角坐标系)如图是广西几个城市旅游景点的平面示意图.
(1)请选取某一个景点为坐标原点,建立平面直角坐标系;
(2)在所建立的平面直角坐标系中,写出其余各景点的坐标.
第七章 平面直角坐标系
7.1 平面直角坐标系
1. D 解析:x轴上的点的纵坐标为0,到y轴的距离为3的点的横坐标是±3,故点 P 的坐标为(3,0)或(-3,0).
2. A 解析:因为点 P 在第二象限,所以 m <0,所以-m>0.又因为点 Q 的纵坐标为0,所以点Q在x轴正半轴上.
3. 1 或5 解析:∵ 点P(3+a,a+1)到x轴的距离是3,∴ |a+1|=3.
∴a+1=3或a+1 = -3.
解得 a=2或a= -4.
当a=2时,3+a=5,点P的坐标为(5,3).当a= -4时,3 +a= -1,点P 的坐标为( -1,-3).
∴点P到y轴的距离为1 或5.
4.7/3解析:由题意,得(2x-1) +(x+3)=0,解得 故点 P 的坐标为 ∴点P到x轴的距离为 .
3065. 解:(1)当ab<0时,有a>0,b<0或a<0,b>0两种情况:
①当a>0,b<0时,点P在第四象限;
②当a<0,b>0时,点P 在第二象限.
(2)当ab=0时,共有三种情况:
①当a=0,b≠0时,点P在y轴上;
②当a≠0,b=0时,点P在x轴上;
③当a=0,b=0时,点P在坐标原点.
6. 解:(1)点C用(2,1)表示,放2 个胡萝卜,1 棵青菜;点 D 用(2,2)表示,放2个胡萝卜,2棵青菜;点 E 用(3,3)表示,放3个胡萝卜,3 棵青菜;点 F 用(3,2)表示,放3 个胡萝卜,2 棵青菜.
(2)走路线①有9个胡萝卜,7 棵青菜;走路线②有10个胡萝卜,8 棵青菜;走路线③有11个胡萝卜,9 棵青菜.故兔子走路线③吃到的食物最多.
7. 解:(1)如图所示:
(2)A(-4,0),B(0,0),C(2,2),D(0,3).
7.2 坐标方法的简单应用
1. A 解析:点沿 x轴的正方向平移,纵坐标不变,所以b=3,横坐标增加2,所以-4+2=a+1,得a= -3.
2.(2,-3) 解析:∵A,B两点的坐标分别为( -2,2),(-3,0),
∴得出坐标轴如图所示.
∴ 点C 的坐标为(2,-3).
3.( -3,1) 解析:根据平面内点的平移规律可得,把“帥”向左平移2个单位长度,向上平移3个单位长度得到“兵”的位置,∴“兵”的坐标为(-1-2,-2+3),即( -3,1).
4.(45,43) 解析:由题意分析可得,
动点P第8=2×4秒运动到(2,0),
动点 P 第24=4×6秒运动到(4,0),
动点P 第48 =6×8秒运动到(6,0),
以此类推,动点 P 第2n(2n+2)秒运动到(2n,0),
∴ 动点 P 第2 024=44×46 秒运动到(44,0),
2 068 -2024 =44.
∴按照运动路线,点P 到达(44,0)后,先向右运动1个单位长度,再向上运动43个单位长度.
∴ 第2 068 秒点 P 所在位置的坐标是(45,43).
5. 解:(1)∵C 为 OP 的中点,
∵OA=2km,
∴与小明家距离相同的是学校和公园.
(2)学校在小明家北偏东45°的方向上,且到小明家的距离为 2km;商场在小明家北偏西 30°的方向上,且到小明家的距离为3.5km;停车场在小明家南偏东60°的方向上,且到小明家的距离为 4km.
6. 解:三角形 A B C 如图所示,A (2,1),B (0,-2),C (6,-5).
2. 解法1:将四边形ABCD 分割成如图①所示的直角三角形和直角梯形.
由各顶点坐标可知DE =3,CE=2,EF =3,CF=5,BF=2,AF=4.
故 3=18.5.
解法2:如图②所示,分别过点A,D作平行于y轴的直线,与过点 C 平行于 x轴的直线交于点 E,F.
由各顶点坐标可知 AB =6,AE =5,CE=4,EF =1,CF=3,DF=2.
故
3. 解:(1)因为
所以a-2=0,b-3=0,c-4=0,
所以a=2,b=3,c=4.
(2)因为
所以 3 -m.
(3)存在.理由如下:
因为 所以3-m=6,解得 m= -3.
所以存在点 使
4. 解:(1)如图①所示,过点 C 作 CM⊥y轴于点M,CN⊥x轴于点 N.
则
=12-1-3-4
=4.
(2)如图②所示,当点P在x轴上时,连接AP.
∵△ABP和△ABC的面积相等,
解得 BP=8.
∵B(2,0),
∴ 当点 P 在点 B 右侧时,2+8=10,故P (10,0);当点 P 在点 B 左侧时,2-8= -6,故 P ( -6,0).如图②所示,当点P在y轴上时,连接BP.
∵△ABP和△ABC的面积相等,
解得 AP=4.
∵A(0,1),
∴ 当点 P 在点A 上方时,1+4=5,故P (0,5);
当点 P 在点 A 下方时,1-4= -3,故P (0,-3).
综上可知,满足条件的点 P 的坐标为(10,0)或( -6,0)或(0,5)或(0,-3).
第七章培优精练
1. A 解析:∵A (-1,1),A (2,1),A (-2,2),A (3,2),A (-3,3),A (4,3),A (-4,4),A (5,4),…,A n (-n,n), A n(n+1,n)(n为正整数),∴2n=2022,解得n=1 011.∴ A 22(1 012,1 011).
2.( ,0)或(
解析:如图,过点 C 作 CE⊥x轴于点 E,则点 E 的坐标为(2,0).根据题意可得 AO =1,OB=3,OE=2,CE=4,DE=1,S四边形ABCD =S三角形AOB + S梯形OBCE+ .设点 P(x,0)( -13. 解:(1)∵直线 PQ∥y轴,
∴2a-2=4.
∴a =3.
∴a+5 =3+5 =8.
∴P(4,8).
(2)∵ 点 P 在第二象限,且它到 x 轴、y轴的距离相等,
∴l2a-21=la+51,2a-2<0,a+5>0.
∴2-2a=a+5.
∴ a = -1.
∴ 原式:
4. 解:(1)如图所示:
(2)如图所示,桂林七星岩的坐标为(4,5),柳州龙潭公园的坐标为(3,3),百色起义纪念馆的坐标为(-2,2),南宁青秀山的坐标为(1,1),钦州三娘湾的坐标为(0,0),北海银滩的坐标为(2,-1).
中小学教育资源及组卷应用平台
7.1 平面直角坐标系
1.(点的坐标)已知x轴上的点P 到y轴的距离为3,则点 P 的坐标为 ( )
A.(3,0) B.(0,3)
C.(0,3)或(0,-3) D.(3,0)或( -3,0)
2.(象限及点的坐标特征)若点 P(m,1)在第二象限,则点 Q(-m,0)在 ( )
A. x轴正半轴上 B. x轴负半轴上
C. y轴正半轴上 D. y轴负半轴上
3. (点的坐标)点 P(3 +a,a+1)到x轴距离为3,则点 P到y轴的距离为 .
4.(象限及点的坐标特征)若点P(2x-1,x+3)在第二、第四象限的角平分线上,则点 P 到x轴的距离为 .
5.(平面直角坐标系,象限及点的坐标特征)已知P(a,b)为平面直角坐标系中的一点.
(1)当ab<0时,点P 处于什么位置
(2)当ab=0时,点P 处于什么位置
6.(有序数对)如图,点 A 用(3,1)表示,并在 A处放3 个胡萝卜,1 棵青菜;点 B 用(2,3)表示,并在 B 处放2 个胡萝下,3 棵青菜.
(1)用有序数对表示点 C,D,E,F,并分别说明各处放几个胡萝卜,几棵青菜;
(2)若一只兔子从点 A 到达点 B(顺着方格线走),有以下几条路线可以选择:①A→C→
D→B;②A→F→D→B;③A→F→E→B.帮可爱的兔子选一条路线,使它吃到的食物最多.
7.(求平面直角坐标系中的图形面积)如图,四边形ABCD所在的网格图中,每个小正方形的边长均为1个单位长度.
(1)建立以点 B 为原点,AB 边所在直线为x轴的平面直角坐标系;
(2)写出点 A,B,C,D 的坐标;
(3)求出四边形 ABCD 的面积.
7.2 坐标方法的简单应用
1. (点的平移)若将点(-4,b)沿x轴的正方向平移2个单位长度得到点(a+1,3),则a,b的值分别是 ( )
A. -3,3 B. -5,3 C. -3,1 D. -5,1
2. (用坐标表示位置)(2021 ·山西中考)如图是一片枫叶标本,其形状呈“掌状五裂型”,裂片具有少数突出的齿,将其放在平面直角坐标系中,表示叶片“顶部”A,B两点的坐标分别为( -2,2),(-3,0),则叶杆“底部”点 C的坐标为 .
3.(用坐标表示位置)中国象棋文化历史久远. 某校开展了以“纵横之间有智慧,攻防转换有乐趣”为主题的中国象棋文化节.如图所示是某次对弈的残局图,如果建立平面直角坐标系,使“帥”位于点(-1,-2),“馬”位于点(2,-2),那么“兵”在同一坐标系下的坐标是 .
4.(规律探究题)如图,动点P 从坐标原点(0,0)出发,以每秒一个单位长度的速度按图中箭头所示方向运动,第1 秒运动到点(1,0),第2 秒运动到点(1,1),第3 秒运动到点(0,1),第4 秒运动到点(0,2),……则第2 068 秒点 P 所在位置的坐标是 .
5. (用方向和距离表示地理位置)下图是小明家和学校所在地的简单地图,已知 OA =2k m,OB=3. 5k m,OP=4km,C 为 OP 的中点,回答下列问题:
(1)图中与小明家距离相同的地方有哪些
(2)请用方向与距离描述学校、商场、停车场相对于小明家的位置.
6.(图形的平移)如图所示,三角形ABC 中任意一点P(a,b)经平移后对应点. 2),将三角形ABC 作同样的平移得到三角形A B C ,求点 A ,B ,C 的坐标.
专项点睛2 在平面直角坐标系中求几何图形的面积
1. 如图,在平面直角坐标系中,已知点A(-1,5),B(-1,0),C(-4,3),则三角形 ABC 的面积为 .
2. 如图所示,在平面直角坐标系中有A,B,C,D四个点,求出四边形ABCD的面积.
3. 如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中 a,b,c满足关系式
(1)求a,b,c的值;
(2)如果在第二象限内有一点 请用含 m 的式子表示四边形 ABOP 的面积;
(3)在(2)的条件下,是否存在点 P,使四边形
ABOP 的面积与三角形ABC 的面积相等 若存在,求出点 P 的坐标;若不存在,请说明理由.
4. 如图所示,已知A(0,1),B(2,0),C(4,3).
(1)求 的面积;
(2)设点 P 在坐标轴上,且 与 的面积相等,求点 P 的坐标.
第七章 培优精练
1.(规律探究题)如图,在平面直角坐标系上有点A(1,0),点 A 第一次跳动至点 A ( -1,1),第二次向右跳动3 个单位长度至点A (2,1),第三次跳动至点 A (-2,2),第四次向右跳动5 个单位长度至点A (3,2),……以此规律跳动下去,点 A 第2 022 次跳动至点 A 22的坐标是 ( )
A.(1012,1 011) B.(1 009,1 008)
C.(1 010,1 009) D.(1 011,1 010)
2.(平面直角坐标系中图形的面积问题)如图,点A( -1,0),B(0,3),C(2,4),D(3,0),P 是线段 AD 上一点,直线CP 将四边形ABCD 的面积分成1:2 的两部分,则点 P 的坐标为 .
3. (平面直角坐标系中点的坐标特征)已知点P(2a-2,a+5),解答下列各题.
(1)若点 Q 的坐标为(4,5),直线 PQ∥y轴,求点 P 的坐标;
(2)若点 P 在第二象限,且它到 x轴、y轴的距离相等,求 的值.
4.(建立适当的平面直角坐标系)如图是广西几个城市旅游景点的平面示意图.
(1)请选取某一个景点为坐标原点,建立平面直角坐标系;
(2)在所建立的平面直角坐标系中,写出其余各景点的坐标.
第七章 平面直角坐标系
7.1 平面直角坐标系
1. D 解析:x轴上的点的纵坐标为0,到y轴的距离为3的点的横坐标是±3,故点 P 的坐标为(3,0)或(-3,0).
2. A 解析:因为点 P 在第二象限,所以 m <0,所以-m>0.又因为点 Q 的纵坐标为0,所以点Q在x轴正半轴上.
3. 1 或5 解析:∵ 点P(3+a,a+1)到x轴的距离是3,∴ |a+1|=3.
∴a+1=3或a+1 = -3.
解得 a=2或a= -4.
当a=2时,3+a=5,点P的坐标为(5,3).当a= -4时,3 +a= -1,点P 的坐标为( -1,-3).
∴点P到y轴的距离为1 或5.
4.7/3解析:由题意,得(2x-1) +(x+3)=0,解得 故点 P 的坐标为 ∴点P到x轴的距离为 .
3065. 解:(1)当ab<0时,有a>0,b<0或a<0,b>0两种情况:
①当a>0,b<0时,点P在第四象限;
②当a<0,b>0时,点P 在第二象限.
(2)当ab=0时,共有三种情况:
①当a=0,b≠0时,点P在y轴上;
②当a≠0,b=0时,点P在x轴上;
③当a=0,b=0时,点P在坐标原点.
6. 解:(1)点C用(2,1)表示,放2 个胡萝卜,1 棵青菜;点 D 用(2,2)表示,放2个胡萝卜,2棵青菜;点 E 用(3,3)表示,放3个胡萝卜,3 棵青菜;点 F 用(3,2)表示,放3 个胡萝卜,2 棵青菜.
(2)走路线①有9个胡萝卜,7 棵青菜;走路线②有10个胡萝卜,8 棵青菜;走路线③有11个胡萝卜,9 棵青菜.故兔子走路线③吃到的食物最多.
7. 解:(1)如图所示:
(2)A(-4,0),B(0,0),C(2,2),D(0,3).
7.2 坐标方法的简单应用
1. A 解析:点沿 x轴的正方向平移,纵坐标不变,所以b=3,横坐标增加2,所以-4+2=a+1,得a= -3.
2.(2,-3) 解析:∵A,B两点的坐标分别为( -2,2),(-3,0),
∴得出坐标轴如图所示.
∴ 点C 的坐标为(2,-3).
3.( -3,1) 解析:根据平面内点的平移规律可得,把“帥”向左平移2个单位长度,向上平移3个单位长度得到“兵”的位置,∴“兵”的坐标为(-1-2,-2+3),即( -3,1).
4.(45,43) 解析:由题意分析可得,
动点P第8=2×4秒运动到(2,0),
动点 P 第24=4×6秒运动到(4,0),
动点P 第48 =6×8秒运动到(6,0),
以此类推,动点 P 第2n(2n+2)秒运动到(2n,0),
∴ 动点 P 第2 024=44×46 秒运动到(44,0),
2 068 -2024 =44.
∴按照运动路线,点P 到达(44,0)后,先向右运动1个单位长度,再向上运动43个单位长度.
∴ 第2 068 秒点 P 所在位置的坐标是(45,43).
5. 解:(1)∵C 为 OP 的中点,
∵OA=2km,
∴与小明家距离相同的是学校和公园.
(2)学校在小明家北偏东45°的方向上,且到小明家的距离为 2km;商场在小明家北偏西 30°的方向上,且到小明家的距离为3.5km;停车场在小明家南偏东60°的方向上,且到小明家的距离为 4km.
6. 解:三角形 A B C 如图所示,A (2,1),B (0,-2),C (6,-5).
2. 解法1:将四边形ABCD 分割成如图①所示的直角三角形和直角梯形.
由各顶点坐标可知DE =3,CE=2,EF =3,CF=5,BF=2,AF=4.
故 3=18.5.
解法2:如图②所示,分别过点A,D作平行于y轴的直线,与过点 C 平行于 x轴的直线交于点 E,F.
由各顶点坐标可知 AB =6,AE =5,CE=4,EF =1,CF=3,DF=2.
故
3. 解:(1)因为
所以a-2=0,b-3=0,c-4=0,
所以a=2,b=3,c=4.
(2)因为
所以 3 -m.
(3)存在.理由如下:
因为 所以3-m=6,解得 m= -3.
所以存在点 使
4. 解:(1)如图①所示,过点 C 作 CM⊥y轴于点M,CN⊥x轴于点 N.
则
=12-1-3-4
=4.
(2)如图②所示,当点P在x轴上时,连接AP.
∵△ABP和△ABC的面积相等,
解得 BP=8.
∵B(2,0),
∴ 当点 P 在点 B 右侧时,2+8=10,故P (10,0);当点 P 在点 B 左侧时,2-8= -6,故 P ( -6,0).如图②所示,当点P在y轴上时,连接BP.
∵△ABP和△ABC的面积相等,
解得 AP=4.
∵A(0,1),
∴ 当点 P 在点A 上方时,1+4=5,故P (0,5);
当点 P 在点 A 下方时,1-4= -3,故P (0,-3).
综上可知,满足条件的点 P 的坐标为(10,0)或( -6,0)或(0,5)或(0,-3).
第七章培优精练
1. A 解析:∵A (-1,1),A (2,1),A (-2,2),A (3,2),A (-3,3),A (4,3),A (-4,4),A (5,4),…,A n (-n,n), A n(n+1,n)(n为正整数),∴2n=2022,解得n=1 011.∴ A 22(1 012,1 011).
2.( ,0)或(
解析:如图,过点 C 作 CE⊥x轴于点 E,则点 E 的坐标为(2,0).根据题意可得 AO =1,OB=3,OE=2,CE=4,DE=1,S四边形ABCD =S三角形AOB + S梯形OBCE+ .设点 P(x,0)( -1
∴2a-2=4.
∴a =3.
∴a+5 =3+5 =8.
∴P(4,8).
(2)∵ 点 P 在第二象限,且它到 x 轴、y轴的距离相等,
∴l2a-21=la+51,2a-2<0,a+5>0.
∴2-2a=a+5.
∴ a = -1.
∴ 原式:
4. 解:(1)如图所示:
(2)如图所示,桂林七星岩的坐标为(4,5),柳州龙潭公园的坐标为(3,3),百色起义纪念馆的坐标为(-2,2),南宁青秀山的坐标为(1,1),钦州三娘湾的坐标为(0,0),北海银滩的坐标为(2,-1).
