人教版七年级数学下册第十章 数据的收集全章同步培优练习(含解析)
文档属性
| 名称 | 人教版七年级数学下册第十章 数据的收集全章同步培优练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-28 00:00:00 | ||
图片预览


文档简介
第十章 数据的收集、整理与描述
中小学教育资源及组卷应用平台
10.1 统计调查
1.(全面调查)下列调查中,适宜采用全面调查方式的是 ( )
A.对某一品牌家具甲醛含量的调查
B.对长江某段水域的水污染情况的调查
C.对全省七年级学生心理健康现状的调查
D.对神舟十四号载人飞船各零件部件的调查
2.(总体,个体,样本,样本容量)要了解七年级1 500 名学生的心理健康情况,从中抽取了 300 名学生的心理健康评估报告进行统计分析,其中“抽取的每名学生的心理健康评估报告”是( )
A. 总体 B.个体 C. 样本 D.样本容量
3. (统计图的综合应用)某校在艺术节选拔节目的过程中,从备选的“街舞”“爵士”“民族”“拉丁”四种类型的舞蹈中,选择一种学生最喜爱的舞蹈,为此,随机调查了本校的部分学生,并将调查结果绘制成如图所示的统计图表(每名学生只选择一种类型),根据统计图表中的信息,解答下列问题:
类型 民族 爵士 拉丁 街舞
所占百分比 a b 30% 15%
(1)求出本次抽样调查的学生人数及 a,b的值.
(2)将条形图补充完整.
(3)若该校共有1500 名学生,则估计全校喜欢“拉丁”舞蹈的学生人数.
4.(统计图的综合应用)绍兴莲花落,又称“莲花乐”“莲花闹”,是绍兴一带的曲艺. 为了解学生对该曲种的熟悉度,某校设置了:非常了解、了解、了解很少、不了解四个选项,随机抽查了部分学生进行问卷调查,要求每名学生只选其中的一项,并将抽查结果绘制成不完整的统计图.
根据图中信息,解答下列问题:
(1)本次接受问卷调查的学生有多少人 并求扇形图中“了解”的扇形圆心角的度数;
(2)全校共有 1 200 名学生,请你估计全校学生中“非常了解”“了解”莲花落的学生共有多少人.
10.2 直方图 10.3 课题学习 从数据谈节水
1. (频率)我校为了更好地开发校本课程,丰富同学们的“第二课堂”,随机调查了50 名七年级同学,其中喜欢剪纸、绘画活动的有 16人,喜欢机器人设计的有12人,喜欢摄影的有10人,其余的喜欢球类运动,则喜欢球类运动的频率是 ( )
A.0.28 B.0.27 C.0.26 D.0.24
2.(频数)将某班女生的身高分成三组,情况如下表所示,则表中a的值是 ( )
第一组 第二组 第三组
频数 6 10 a
百分比 b C 20%
A.2 B.4 C.6 D.8
3.(频数分布直方图)七(3)班共有50 名同学,下图是该班一次体育模拟测试成绩的频数分布直方图(满分为 30 分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是 .
4.(频数分布表,频数分布直方图)某市农科所为了考察某种水稻穗长的分布情况,在一块试验田里随机抽取了50 个谷穗作为样本,量得它们的长度(单位:cm),对样本数据适当分组后,列出了如下频数分布表:
穗长/cm 4.5≤x<5 5≤x<5.5 5.5≤x<6
频数 4 8 12
穗长/cm 6≤x<6.5 6.5≤x<7 7≤x<7.5
频数 13 10 3
(1)画频数分布直方图;
(2)请你对这块试验田的水稻穗长进行分析;
(3)计算出这块试验田里,穗长在5.5cm≤x <7 cm范围内的谷穗所占的百分比.
5.(频数分布表,频数分布直方图)为了解2 月份某小区家庭用电情况,随机抽取了该小区部分家庭2月份电费金额进行调查,并将数据进行了如下整理,请根据所提供的信息,解答下列问题:
月用电费/元 频数/户 频率
10≤x<100 12 0.24
100≤x<200 18 n
200≤x<300 m 0.20
300≤x<400 6 0.12
400≤x<500 4 0.08
(1)求m,n,并把频数分布直方图补充完整;
(2)求在被调查的家庭中,该小区2月份所用电费少于300元的家庭占被调查家庭总数的百分比;
(3)若该小区有1000 户家庭,根据调查数据估计,该小区2月份电费不少于300 元的家庭大约有多少户
专项点睛5 三种常见的统计图
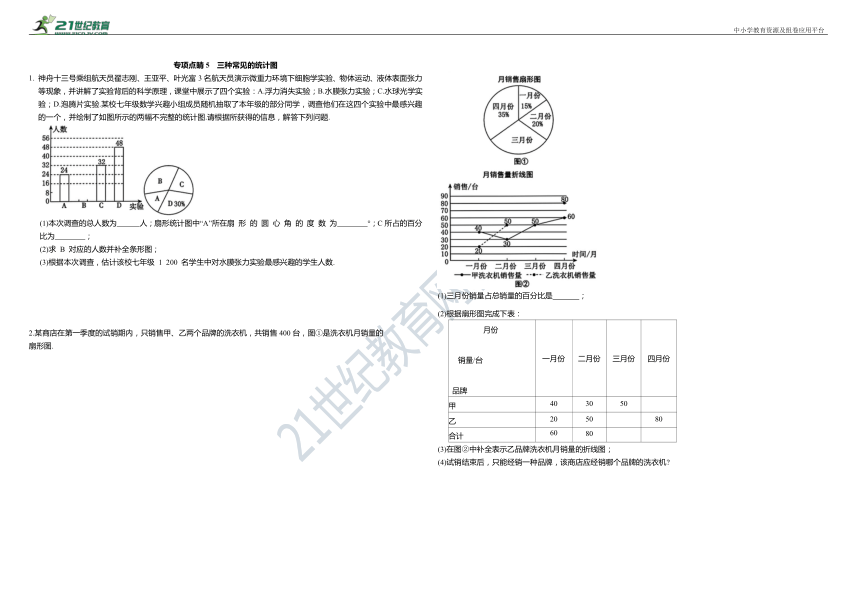
1. 神舟十三号乘组航天员翟志刚、王亚平、叶光富3名航天员演示微重力环境下细胞学实验、物体运动、液体表面张力等现象,并讲解了实验背后的科学原理,课堂中展示了四个实验:A.浮力消失实验;B.水膜张力实验;C.水球光学实验;D.泡腾片实验.某校七年级数学兴趣小组成员随机抽取了本年级的部分同学,调查他们在这四个实验中最感兴趣的一个,并绘制了如图所示的两幅不完整的统计图.请根据所获得的信息,解答下列问题.
(1)本次调查的总人数为 人;扇形统计图中“A”所在扇 形 的 圆 心 角 的 度 数 为 °;C所占的百分比为 ;
(2)求 B 对应的人数并补全条形图;
(3)根据本次调查,估计该校七年级 1 200 名学生中对水膜张力实验最感兴趣的学生人数.
2.某商店在第一季度的试销期内,只销售甲、乙两个品牌的洗衣机,共销售400台,图①是洗衣机月销量的
扇形图.
(1)三月份销量占总销量的百分比是 ;
(2)根据扇形图完成下表:
月份 销量/台 品牌 一月份 二月份 三月份 四月份
甲 40 30 50
乙 20 50 80
合计 60 80
(3)在图②中补全表示乙品牌洗衣机月销量的折线图;
(4)试销结束后,只能经销一种品牌,该商店应经销哪个品牌的洗衣机
第十章培优精练
1. (抽样调查)下列调查,其中适合用抽样调查的个数有( )
①为了检测一批电视机的使用寿命;
②为了调查全国平均几人拥有一部手机;
③为了解全区学生的平均上网时间;
④“辽宁号”航母下海前对重要零部件的检查.
A.1个 B.2个 C.3个 D.4个
2.(统计图)某校为提高学生的综合素养,准备开展摄影、书法、绘画、表演、手工五类社团活动. 为了对此项活动进行统筹安排,随机抽取了部分学生进行调查,要求每人从五个类别中只选择一个,将调查结果绘制成了两幅统计图(未完成).请根据统计图中的信息,解答下列问题:
(1)本次共调查了 名学生;
(2)请将条形图补充完整;
(3) 扇 形 图 中,“ 摄 影”所 占 的 百 分 比为 ;“手工”所对应的圆心角的度数为 ;
(4)若该校共有2 700 名学生,请估计选择“绘画”的学生人数.
3.(频数分布直方图)某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:h)进行分组整理,并绘制了如图所示的不完整的频数直方图和扇形图:
根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图;
(2)求扇形图中 m 的值和 E 组对应的圆心角度数;
(3)请估计该校3 000 名学生中每周的课外阅读时间不少于6h的人数.
第十章 数据的收集、整理与描述
10.1 统计调查
1. D 解析:A.对某一品牌家具甲醛含量的调查,适合采用抽样调查,选项不符合题意;
B.对长江某段水域的水污染情况的调查,适合采用抽样调查,选项不符合题意;
C.对全省七年级学生心理健康现状的调查,适合采用抽样调查,选项不符合题意;
D.对神舟十四号载人飞船各零件部件的调查,适合采用全面调查,选项符合题意;故选 D.
2. B
3. 解:(1)本次抽样调查的学生人数为 60 ÷30% =200(人),a=50÷200=25% ,200-50-60-30 =60,b=60÷200=30%.
(2)补全条形图如图所示:
(3)1 500×30% =450(人).
答:估计全校有450人喜欢“拉丁”舞蹈.
4. 解:(1)接受问卷调查的学生有90÷45% =200(人).
“了解”的扇形圆心角的度数为
(2)“非常了解”的学生有200×15% =30(人).
(人).
答:估计全校学生中“非常了解”“了解”莲花落的学生共有600人.
10.2 直方图
10.3 课题学习 从数据谈节水
1. D 解析:由题意,得50-16-12-10=12,
∴ 12÷50=0.24.
∴喜欢球类运动的频率是0.24,故选 D.
2. B 解析:第一组和第二组所占的百分比为 1 -20% =80% ,则女生的总人数为(6 + 10) ÷80% =20(人),所以第三组的人数为 20×20% =4(人),即a=4.
3. 92% 解析:由题图中可以看出成绩不低于23 分的人数为6+4 +14+22=46(人),占全班人数的百分比为
4. 解:(1)如图所示.
(2)由(1)可知谷穗长度大部分落在5cm 至 7 c m之间,在6cm≤x <6.5cm 范围内的谷穗最多,在4.5cm ≤x<5cm、7cm≤x<7.5cm 范围内的较少.(答案不唯一,合理即可)
(3)在这块试验田里,穗长在5.5cm ≤x<7 cm范围内的谷穗所占的百分比为(12 + 13 + 10) ÷50×100% =70%.
答:这块试验田里,穗长在5.5cm≤x<7 cm范围内的谷穗所占的百分比为70%.
5. 解:(1)12÷0.24 =50(户),
m=50×0.20=10(户),
n=18÷50=0.36.
故 m=10,n=0.36.
补全频数分布直方图如下:
(2)0.24+0.36 +0.20=0.80 =80%.
答:在被调查的家庭中,该小区2月份所用电费少于300元的家庭占被调查家庭总数的百分比为80%.
(3)1 000×(0.12 +0.08) =200(户).
答:该小区1000户家庭中2月份电费不少于300 元的家庭大约有 200 户.
专项点睛5 三种常见的统计图
1. 解:(1)本次调查的总人数为48÷30% =160(人).
扇形统计图中“A”所在扇形的圆心角的度数为
C所占的百分比为
故答案为160;54;20%.
(2)B对应人数为 160-24-32-48 =56(人),补全条形图如下:
(人).
答:对水膜张力实验最感兴趣的学生人数约为420 人.
2. 解:(1)三月份销量占总销量的百分比是 1 -15% -20% -35% =30%.
故答案为30%.
(2)三月份乙品牌洗衣机月销量为(30 + 50) ÷20% ×30% -50=70(台).四月份甲品牌洗衣机月销量为60 台.
三月份合计销量为50+70=120(台).
四月份合计销量为60+80=140(台).
填表如下:
月份 销量/台 品牌 一月份 二月份 三月份 四月份
甲 40 30 50 60
乙 20 50 70 80
合计 60 80 120 140
(3)补全表示乙品牌洗衣机月销量的折线图如下:月销售量折线图
(4)根据折线统计图可得,乙品牌洗衣机销售量始终处于上升趋势,甲品牌洗衣机销售量出现过下降趋势,故该商店应选择乙品牌洗衣机.
第十章 培优精练
1. C 解析:①为了检测一批电视机的使用寿命适合使用抽样调查;
②为了调查全国平均几人拥有一部手机适合使用抽样调查;
③为了解全区学生的平均上网时间适合使用抽样调查;
④“辽宁号”航母下海前对重要零部件的检查适合使用全面调查. 故选 C.
2. 解:(1)本次共调查学生 180÷30% =600(名),故答案为600.
(2)表演类的人数为600×20% =120(名).
手工类的人数为600-90-180-150-120=60(名).
故补全条形图如图所示:
(3)在扇形图中,“摄影”所占的百分比为 100% =15%;
“手工”所对应的圆心角的度数为 故答案为 15% ;36°.
(名).
答:估计选择“绘画”的学生人数为675 名.
3. 解:(1)调查的总人数为 10÷10% =100(人),D组的人数为 100×25% =25(人).
补全的频数分布直方图如图所示.
故扇形图中的 m =40.扇形图中 E 组对应的圆心角度数为
(3)样本中每周的课外阅读时间不少于6h的人数占样本总数的 所以估计该校3 000名学生中每周的课外阅读时间不少于6h的人数为3000×29% =870(人).
中小学教育资源及组卷应用平台
10.1 统计调查
1.(全面调查)下列调查中,适宜采用全面调查方式的是 ( )
A.对某一品牌家具甲醛含量的调查
B.对长江某段水域的水污染情况的调查
C.对全省七年级学生心理健康现状的调查
D.对神舟十四号载人飞船各零件部件的调查
2.(总体,个体,样本,样本容量)要了解七年级1 500 名学生的心理健康情况,从中抽取了 300 名学生的心理健康评估报告进行统计分析,其中“抽取的每名学生的心理健康评估报告”是( )
A. 总体 B.个体 C. 样本 D.样本容量
3. (统计图的综合应用)某校在艺术节选拔节目的过程中,从备选的“街舞”“爵士”“民族”“拉丁”四种类型的舞蹈中,选择一种学生最喜爱的舞蹈,为此,随机调查了本校的部分学生,并将调查结果绘制成如图所示的统计图表(每名学生只选择一种类型),根据统计图表中的信息,解答下列问题:
类型 民族 爵士 拉丁 街舞
所占百分比 a b 30% 15%
(1)求出本次抽样调查的学生人数及 a,b的值.
(2)将条形图补充完整.
(3)若该校共有1500 名学生,则估计全校喜欢“拉丁”舞蹈的学生人数.
4.(统计图的综合应用)绍兴莲花落,又称“莲花乐”“莲花闹”,是绍兴一带的曲艺. 为了解学生对该曲种的熟悉度,某校设置了:非常了解、了解、了解很少、不了解四个选项,随机抽查了部分学生进行问卷调查,要求每名学生只选其中的一项,并将抽查结果绘制成不完整的统计图.
根据图中信息,解答下列问题:
(1)本次接受问卷调查的学生有多少人 并求扇形图中“了解”的扇形圆心角的度数;
(2)全校共有 1 200 名学生,请你估计全校学生中“非常了解”“了解”莲花落的学生共有多少人.
10.2 直方图 10.3 课题学习 从数据谈节水
1. (频率)我校为了更好地开发校本课程,丰富同学们的“第二课堂”,随机调查了50 名七年级同学,其中喜欢剪纸、绘画活动的有 16人,喜欢机器人设计的有12人,喜欢摄影的有10人,其余的喜欢球类运动,则喜欢球类运动的频率是 ( )
A.0.28 B.0.27 C.0.26 D.0.24
2.(频数)将某班女生的身高分成三组,情况如下表所示,则表中a的值是 ( )
第一组 第二组 第三组
频数 6 10 a
百分比 b C 20%
A.2 B.4 C.6 D.8
3.(频数分布直方图)七(3)班共有50 名同学,下图是该班一次体育模拟测试成绩的频数分布直方图(满分为 30 分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是 .
4.(频数分布表,频数分布直方图)某市农科所为了考察某种水稻穗长的分布情况,在一块试验田里随机抽取了50 个谷穗作为样本,量得它们的长度(单位:cm),对样本数据适当分组后,列出了如下频数分布表:
穗长/cm 4.5≤x<5 5≤x<5.5 5.5≤x<6
频数 4 8 12
穗长/cm 6≤x<6.5 6.5≤x<7 7≤x<7.5
频数 13 10 3
(1)画频数分布直方图;
(2)请你对这块试验田的水稻穗长进行分析;
(3)计算出这块试验田里,穗长在5.5cm≤x <7 cm范围内的谷穗所占的百分比.
5.(频数分布表,频数分布直方图)为了解2 月份某小区家庭用电情况,随机抽取了该小区部分家庭2月份电费金额进行调查,并将数据进行了如下整理,请根据所提供的信息,解答下列问题:
月用电费/元 频数/户 频率
10≤x<100 12 0.24
100≤x<200 18 n
200≤x<300 m 0.20
300≤x<400 6 0.12
400≤x<500 4 0.08
(1)求m,n,并把频数分布直方图补充完整;
(2)求在被调查的家庭中,该小区2月份所用电费少于300元的家庭占被调查家庭总数的百分比;
(3)若该小区有1000 户家庭,根据调查数据估计,该小区2月份电费不少于300 元的家庭大约有多少户
专项点睛5 三种常见的统计图
1. 神舟十三号乘组航天员翟志刚、王亚平、叶光富3名航天员演示微重力环境下细胞学实验、物体运动、液体表面张力等现象,并讲解了实验背后的科学原理,课堂中展示了四个实验:A.浮力消失实验;B.水膜张力实验;C.水球光学实验;D.泡腾片实验.某校七年级数学兴趣小组成员随机抽取了本年级的部分同学,调查他们在这四个实验中最感兴趣的一个,并绘制了如图所示的两幅不完整的统计图.请根据所获得的信息,解答下列问题.
(1)本次调查的总人数为 人;扇形统计图中“A”所在扇 形 的 圆 心 角 的 度 数 为 °;C所占的百分比为 ;
(2)求 B 对应的人数并补全条形图;
(3)根据本次调查,估计该校七年级 1 200 名学生中对水膜张力实验最感兴趣的学生人数.
2.某商店在第一季度的试销期内,只销售甲、乙两个品牌的洗衣机,共销售400台,图①是洗衣机月销量的
扇形图.
(1)三月份销量占总销量的百分比是 ;
(2)根据扇形图完成下表:
月份 销量/台 品牌 一月份 二月份 三月份 四月份
甲 40 30 50
乙 20 50 80
合计 60 80
(3)在图②中补全表示乙品牌洗衣机月销量的折线图;
(4)试销结束后,只能经销一种品牌,该商店应经销哪个品牌的洗衣机
第十章培优精练
1. (抽样调查)下列调查,其中适合用抽样调查的个数有( )
①为了检测一批电视机的使用寿命;
②为了调查全国平均几人拥有一部手机;
③为了解全区学生的平均上网时间;
④“辽宁号”航母下海前对重要零部件的检查.
A.1个 B.2个 C.3个 D.4个
2.(统计图)某校为提高学生的综合素养,准备开展摄影、书法、绘画、表演、手工五类社团活动. 为了对此项活动进行统筹安排,随机抽取了部分学生进行调查,要求每人从五个类别中只选择一个,将调查结果绘制成了两幅统计图(未完成).请根据统计图中的信息,解答下列问题:
(1)本次共调查了 名学生;
(2)请将条形图补充完整;
(3) 扇 形 图 中,“ 摄 影”所 占 的 百 分 比为 ;“手工”所对应的圆心角的度数为 ;
(4)若该校共有2 700 名学生,请估计选择“绘画”的学生人数.
3.(频数分布直方图)某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:h)进行分组整理,并绘制了如图所示的不完整的频数直方图和扇形图:
根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图;
(2)求扇形图中 m 的值和 E 组对应的圆心角度数;
(3)请估计该校3 000 名学生中每周的课外阅读时间不少于6h的人数.
第十章 数据的收集、整理与描述
10.1 统计调查
1. D 解析:A.对某一品牌家具甲醛含量的调查,适合采用抽样调查,选项不符合题意;
B.对长江某段水域的水污染情况的调查,适合采用抽样调查,选项不符合题意;
C.对全省七年级学生心理健康现状的调查,适合采用抽样调查,选项不符合题意;
D.对神舟十四号载人飞船各零件部件的调查,适合采用全面调查,选项符合题意;故选 D.
2. B
3. 解:(1)本次抽样调查的学生人数为 60 ÷30% =200(人),a=50÷200=25% ,200-50-60-30 =60,b=60÷200=30%.
(2)补全条形图如图所示:
(3)1 500×30% =450(人).
答:估计全校有450人喜欢“拉丁”舞蹈.
4. 解:(1)接受问卷调查的学生有90÷45% =200(人).
“了解”的扇形圆心角的度数为
(2)“非常了解”的学生有200×15% =30(人).
(人).
答:估计全校学生中“非常了解”“了解”莲花落的学生共有600人.
10.2 直方图
10.3 课题学习 从数据谈节水
1. D 解析:由题意,得50-16-12-10=12,
∴ 12÷50=0.24.
∴喜欢球类运动的频率是0.24,故选 D.
2. B 解析:第一组和第二组所占的百分比为 1 -20% =80% ,则女生的总人数为(6 + 10) ÷80% =20(人),所以第三组的人数为 20×20% =4(人),即a=4.
3. 92% 解析:由题图中可以看出成绩不低于23 分的人数为6+4 +14+22=46(人),占全班人数的百分比为
4. 解:(1)如图所示.
(2)由(1)可知谷穗长度大部分落在5cm 至 7 c m之间,在6cm≤x <6.5cm 范围内的谷穗最多,在4.5cm ≤x<5cm、7cm≤x<7.5cm 范围内的较少.(答案不唯一,合理即可)
(3)在这块试验田里,穗长在5.5cm ≤x<7 cm范围内的谷穗所占的百分比为(12 + 13 + 10) ÷50×100% =70%.
答:这块试验田里,穗长在5.5cm≤x<7 cm范围内的谷穗所占的百分比为70%.
5. 解:(1)12÷0.24 =50(户),
m=50×0.20=10(户),
n=18÷50=0.36.
故 m=10,n=0.36.
补全频数分布直方图如下:
(2)0.24+0.36 +0.20=0.80 =80%.
答:在被调查的家庭中,该小区2月份所用电费少于300元的家庭占被调查家庭总数的百分比为80%.
(3)1 000×(0.12 +0.08) =200(户).
答:该小区1000户家庭中2月份电费不少于300 元的家庭大约有 200 户.
专项点睛5 三种常见的统计图
1. 解:(1)本次调查的总人数为48÷30% =160(人).
扇形统计图中“A”所在扇形的圆心角的度数为
C所占的百分比为
故答案为160;54;20%.
(2)B对应人数为 160-24-32-48 =56(人),补全条形图如下:
(人).
答:对水膜张力实验最感兴趣的学生人数约为420 人.
2. 解:(1)三月份销量占总销量的百分比是 1 -15% -20% -35% =30%.
故答案为30%.
(2)三月份乙品牌洗衣机月销量为(30 + 50) ÷20% ×30% -50=70(台).四月份甲品牌洗衣机月销量为60 台.
三月份合计销量为50+70=120(台).
四月份合计销量为60+80=140(台).
填表如下:
月份 销量/台 品牌 一月份 二月份 三月份 四月份
甲 40 30 50 60
乙 20 50 70 80
合计 60 80 120 140
(3)补全表示乙品牌洗衣机月销量的折线图如下:月销售量折线图
(4)根据折线统计图可得,乙品牌洗衣机销售量始终处于上升趋势,甲品牌洗衣机销售量出现过下降趋势,故该商店应选择乙品牌洗衣机.
第十章 培优精练
1. C 解析:①为了检测一批电视机的使用寿命适合使用抽样调查;
②为了调查全国平均几人拥有一部手机适合使用抽样调查;
③为了解全区学生的平均上网时间适合使用抽样调查;
④“辽宁号”航母下海前对重要零部件的检查适合使用全面调查. 故选 C.
2. 解:(1)本次共调查学生 180÷30% =600(名),故答案为600.
(2)表演类的人数为600×20% =120(名).
手工类的人数为600-90-180-150-120=60(名).
故补全条形图如图所示:
(3)在扇形图中,“摄影”所占的百分比为 100% =15%;
“手工”所对应的圆心角的度数为 故答案为 15% ;36°.
(名).
答:估计选择“绘画”的学生人数为675 名.
3. 解:(1)调查的总人数为 10÷10% =100(人),D组的人数为 100×25% =25(人).
补全的频数分布直方图如图所示.
故扇形图中的 m =40.扇形图中 E 组对应的圆心角度数为
(3)样本中每周的课外阅读时间不少于6h的人数占样本总数的 所以估计该校3 000名学生中每周的课外阅读时间不少于6h的人数为3000×29% =870(人).
