人教版七年级数学下册第八章 二元一次方程组全章同步培优练习(含解析)
文档属性
| 名称 | 人教版七年级数学下册第八章 二元一次方程组全章同步培优练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 717.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-28 14:18:31 | ||
图片预览




文档简介
第八章 二元一次方程组
中小学教育资源及组卷应用平台
8.1 二元一次方程组
1. (二元一次方程组的实际应用)《九章算术》是人类科学史上应用数学的“算经之首”,书中记载:今有三人共车,二车空;二人共车,九人步. 问:人与车各几何 译文:若3人坐一辆车,则两辆车是空的;若2人坐一辆车,则9人需要步行,问:人与车各多少 设有 x辆车,人数为y,根据题意可列方程组为 ( )
2.(二元一次方程组的解)写出一个唯一解为 的二元一次方程组是 .
3. (二元一次方程组的实际应用,图表信息题)根据图给出的信息,求每件 T 恤衫和每瓶矿泉水的价格(只列方程组).
4.(一元一次方程组的错解问题)小明在做家庭作业时发现练习册上一道解方程的题目被墨水污染, “□”和“△”表示被污染的内容,他翻开书后面的答案,这道题的解是 你能帮助他补上“□”和“△”的内容吗 写出你的方法.
5.(二元一次方程特殊解的实际应用)某同学去面包店买面包,面包有 A,B 两种包装,每个面包品质相同,且只能整盒购买,商品信息如下:
A包装盒 B 包装盒
每盒面包个数/个 3 8
每盒价格/元 5 11
若某同学正好买了50个面包,则他最少需要花多少元
8.2 消元——解二元一次方程组
1. (解二元一次方程组的方法)解方程组① 比较简便的方法是 ( )
A.都用代入法
B.都用加减法
C.①用代入法,②用加减法
D.①用加减法,②用代入法
2.(二元一次方程组的解)m为正整数,已知二元一次方程组 有整数解,则 的值为( )
A.3 或48 B.3
C.4 或49 D.48
3.(二元一次方程组的实际应用)如图,在长为15,宽为12 的长方形中,有形状、大小完全相同的5个小长方形,则图中阴影部分的面积为 ( )
A.35 B.45 C.55 D.65
4. (关于二元一次方程组的新定义型问题)对于实数x,y定义新运算x*y=ax +by+1,其a,b为常数,等式右边为通常的加法和乘法运算,若3*5=15,4*7=28,则5*9= .
5. (解二元一次方程组的)(2022·广东汕头澄海区期末)已知关于x,y 的二元一次方程组 的解为 那么关于 m,n的二元一次方程组 的解为 .
6.(解二元一次方程组)解下列方程组:
7.(解含参的二元一次方程组)已知关于a,b的二元一次方程组 ②且 abc≠0,求 的值.
8.3 实际问题与二元一次方程组
1. (计分问题)小方、小红和小军三人玩飞镖游戏,各投四支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小红的得分是 ( )
A.30分 B.32分
C.33 分 D.34分
2.(数字问题)一个两位数,它的个位数字是十位数字的2倍,且十位数字与个位数字和的3 倍比这个两位数小3,则这个两位数是 .
3.(古算问题)(2021·湖南邵阳中考)《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有共买物,人出八,盈三;人出七,不足四. 问人数、物价各几何 意思是:几个人一起去购买某物品,如果每人出8 钱,则多了3钱;如果每人出7钱,则少了4 钱.问有多少人,物品的价值是多少 该问题中物品的价值是 钱.
4.(行程问题)林芳沿公路匀速前进,每隔 4min就迎面开来一辆公共汽车,每隔6m in就有一辆公共汽车从背后超过她,假定公共汽车的速度不变,而且迎面开来的相邻两车的距离和从背后开来的相邻两车的距离都是1 200 m,求林芳的速度和公共汽车的速度.
5.(实际应用问题)“绿水青山就是金山银山”,科学研究表明:树叶在光合作用后产生的分泌物能够吸附空气中的悬浮颗粒物,具有滞尘净化空气的作用.已知一片银杏树叶一年的平均滞尘量比一片国槐树叶一年的平均滞尘量的2 倍少4m g,若一片国槐树叶与一片银杏树叶一年的平均滞尘总量为 62 mg.
(1)请分别求出一片国槐树叶和一片银杏树叶一年的平均滞尘量;
(2)娄底市双峰县九峰山森林公园某处有始于唐代的三棵银杏树,据估计三棵银杏树共有约50 000 片树叶.问这三棵银杏树一年的平均滞尘总量约多少千克.
6. (利润问题)某地区 2020年进出口总额为520 亿元,2021 年进出口总额比 2020 年有所增加,其中进口额增加了25% ,出口额增加了 30%.
注:进出口总额 =进口额 + 出口额.
(1)设 2020 年进口额为 x 亿元,出口额为y亿元,请用含x,y的代数式填表:
年份 进口额/亿元 出口额/ 亿元 进出口总额/亿元
2020 x y 520
2021 1.25x 1.3y
(2)已知 2021 年进出口总额比 2020 年增加了140亿元,求2021 年进口额和出口额分别是多少亿元
*8.4 三元一次方程组的解法
1. (三元一次方程组的求解)已知 x +4y-3z=0,且4x-5y+2z=0,则x:y:z为 ( )
A.1:2:3 B.1:3:2
C.2:1:3 D.3:1:2
2. (三元一次方程组的求解)若( ,则x+y+z等于( )
B. C.2 D. -2
3. (三元一次方程组的求解,同类项) 已知 与 是同类项,则x= ,y= ,z =
4.(三元一次方程组的实际应用)某中学举办的足球赛规定胜一场得3分,平一场得1分,负一场得0分,在这次足球赛中,八(1)班足球队共参加了8场比赛,其中平的场数是负的场数 的 2 倍,共得 17 分, 则该 队 负 了 场.
5. (三元一次方程组的求解) 给定 方程组
口果令 则
方程组 由此解得 对不对 为什么
6. (三元一次方程组的应用,数字问题)有一个三位数,个位数字是百位数字的3 倍,十位数字比百位数字大5,若将此数的个位数与百位数互相对调,所得新数比原数的2 倍多35,求原数.
7.(三元一次方程组的实际应用)为确保信息安全,在传输时往往需加密,发送方发出一组密码a,b,c时,接收方对应收到的密码为A,B,C.双方约定:A=2a-b,B=2b,C=b+c,例如:发出1,2,3,则收到0,4,5.
(1)当发送方发出一组密码为2,3,5时,接收方收到的密码是多少
(2)当接收方收到一组密码为2,8,11 时,发送方发出的密码是多少
专项点睛3 二元一次方程组与图表信息问题
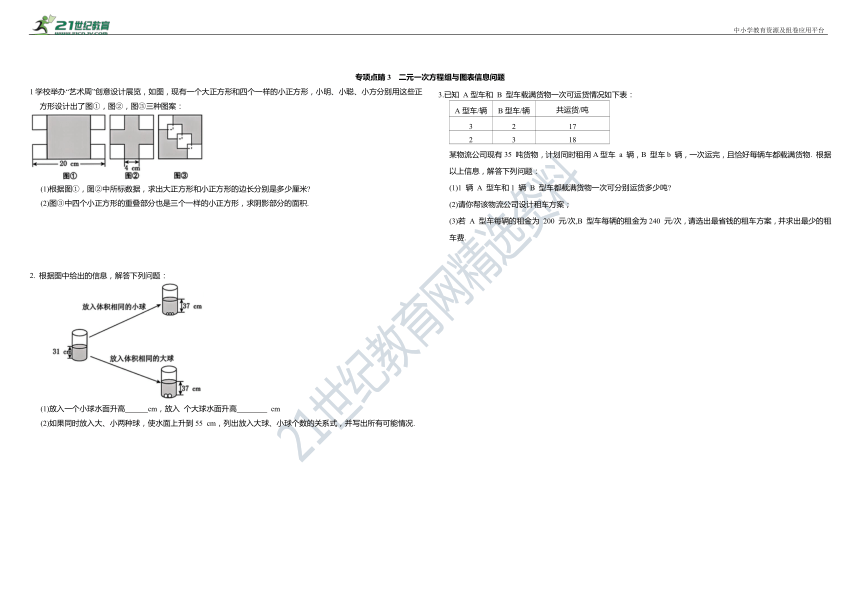
1学校举办“艺术周”创意设计展览,如图,现有一个大正方形和四个一样的小正方形,小明、小聪、小方分别用这些正方形设计出了图①,图②,图③三种图案:
(1)根据图①,图②中所标数据,求出大正方形和小正方形的边长分别是多少厘米
(2)图③中四个小正方形的重叠部分也是三个一样的小正方形,求阴影部分的面积.
2. 根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高 cm,放入 个大球水面升高 cm
(2)如果同时放入大、小两种球,使水面上升到55 cm,列出放入大球、小球个数的关系式,并写出所有可能情况.
3.已知 A型车和 B 型车载满货物一次可运货情况如下表:
A型车/辆 B型车/辆 共运货/吨
3 2 17
2 3 18
某物流公司现有35 吨货物,计划同时租用A型车 a 辆,B 型车b 辆,一次运完,且恰好每辆车都载满货物. 根据以上信息,解答下列问题:
(1)1 辆 A 型车和1 辆 B 型车都载满货物一次可分别运货多少吨
(2)请你帮该物流公司设计租车方案;
(3)若 A 型车每辆的租金为 200 元/次,B 型车每辆的租金为240 元/次,请选出最省钱的租车方案,并求出最少的租车费.
第八章 培优精练
1.(二元一次方程组的同解问题)若方程组 と、 有相同的解,则a,b的值为( )
A.2,3 B.3,2 C.2, -1 D. -1,2
2.(三元一次方程组的求解)已知 且 则a = ,b= ,c = .
3.(二元一次方程组的实际应用)端午节是中国传统节日,人们有吃粽子的习俗. 某商场从6 月 12 日起开始打折促销,肉粽六折,白粽七折,打折前购买4 盒肉粽和5 盒白粽需350元,打折后购买5盒肉粽和10 盒白粽需 360 元. 轩轩同学想为敬老院送肉粽和白粽各5盒,则他在6月13 日购买的花费比在打折前购买节省 元.
4.(二元一次方程组的求解)解下列方程组:
5.(二元一次方程组的错解问题)甲、乙两人解方 程 组 甲 因 看 错 a, 解得 乙将其中一个方程的b写成了它的相反数,解得 求 a,b 的值.
6.(二元一次方程组的实际应用)某工厂生产如图①所示的长方形和正方形纸板,做成如图②所示的竖式与横式两种长方体形状的无盖纸盒,其中竖式纸盒由4个长方形和1个正方形纸板做成,横式纸盒由 3 个长方形和2 个正方形纸板做成(给定的长方形和正方形纸板都不用裁剪,也不考虑接缝).
(1)现有长方形纸板340 张,正方形纸板160张,做成上述两种纸盒,纸板恰好用完,求两种纸盒的生产个数.
(2)纸板车间共有78 名工人,每个工人一天能生产 70 张长方形纸板或者 100 张正方形纸板,已知一个竖式纸盒与一个横式纸盒配套,要求纸板车间一天生产的纸板由其他车间做成竖式纸盒与横式纸盒配套,问纸板车间应该如何安排工人生产两种纸板
第八章 二元一次方程组
8.1 二元一次方程组
1. B
(答案不唯一)
解析:因为x=1,y=2,
所以2x+y=4,3x-2y= -1.
故 有唯一的解是
3. 解:设每件T 恤衫x元,每瓶矿泉水y元.
由题意得
4. 解:因为方程组的解为 所以把 分别代入方程组的每一个方程,得□=3×2 -2×( -1) =6+2=8,△=5×2+( -1) =10-1=9.
5. 解:设购买 A 包装面包x盒,B包装面包y盒.
由题意得3x+8y=50.
∵x,y为非负整数或
当x=6,y=4时,费用为5×6+11×4=74(元);
当x=14,y=1时,费用为5×14+11×1 =81(元).
∵74<81,
∴某同学正好买了 50 个面包,则他最少需要花74 元.
8.2 消元———解二元一次方程组
1. C 解析:①中的第一个方程为y=x-3,用代入法比较简便;②中的x的系数相等,用加减法比较简便.故选 C.
2. B 解析:
①+②,得(m+3)x=10,解得
把 代入②,得
由方程组有整数解,得m+3= ±1,m+3= ±5,
解得m = -2,-4,2,-8.
由m为正整数,得m=2,
则 故选 B.
3. B 解析:设小长方形的长为x,宽为 y.
根据题意,得 解得
所以
4.41 解析:由题意知,若3*5=15,4*7=28,则 解得 所以5*9= -37×5+25×9+1 =41.
解析:∵ 关于 x,y 的二元一次方程组 的解为
∴ 可 以 把 关 于 m, n 的 二 元 一 次 方 程 组 中的(m+n)看成x,(m-n)看成y,
解得
6. 解:(1)原方程组整理可得
①-②,得4y= -28,解得y= -7.
将y= -7代入①,得3x+7= -8.
解得x= -5.
故原方程组的解为
(2)原方程组整理得
①×2+②,得5x=10,解得x=2.
把x=2代入①,得2-y=-1.
解得y=3.
故原方程组的解为
(3)设 则 x =3k,y=4k. 把 x =3k,y =4k代入x+2y=11,得3k+2×4k=11,解得k=1,即x=3k=3,y=4k=4,所以原方程组的解为
7. 解:①+②,得3a-b= -5c.③
②-①,得a-5b= -11c.④
④×2,得2a-10b= -22c.⑤
将③和⑤代)入
得
8.3 实际问题与二元一次方程组
1. B 解析:设掷中 A 区、B区一次的得分分别为x分,y分.
依据题意,得 解得
所以小红的得分是5+3×9=32(分).
2. 12 解析:设个位数字为x,十位数字为y. 由题意,得 解得 则这个两位数是 12.
3.53 解析:设有x人,物品的价值为y钱. 依据题意,得 解得 即该问题中物品的价值是 53 钱.
4. 解:设林芳的速度为 x m/min,公共汽车的速度为y m/min.
由题意,得 解得
答:林芳的速度为 50 m/min,公共汽车的速度为250 m/min.
5. 解:(1)设一片银杏树叶一年的平均滞尘量为 x mg,一片国槐树叶一年的平均滞尘量为y mg.
由题意得
解得
答:一片银杏树叶一年的平均滞尘量为40 mg,一片国槐树叶一年的平均滞尘量为22 mg.
(2)50 000×40=2000 000(mg) =2kg.
答:这三棵银杏树一年的平均滞尘总量约为2k g.
6. 解:(1)1.25x+1.3y
(2)由题意得 解得
∴ 1.25x=400,1.3y=260.
答:2021 年进口额是400亿元,出口额是260 亿元.
*8.4 三元一次方程组的解法
1. A 解析:组成方程组 と①×5+②×4,得21x=7z,解得 代入①得 则
2. A 解析:∵ 解得 则
3.6;8;3 解析:由题意,得
由①+②,得2y=16,解得y=8.
由①+③,得2x=12,解得x=6.
由②+③,得2z=6,解得z=3.
4. 1 解析:设八(1)班足球队胜了x场,平了y场,负了z场,由题意,得 解得 即八(1)班足球队负了1场.
5. 解:不对.
理由:方程组
由①+②+③,得2(A+B+C)=8.
所以A+B+C=4.④
由④-①,得C=3.
由④-②,得A=2.
由④-③,得B= -1.
即
由此可见题目中给出的答案不对.
6. 解:设个位数字为x,十位数字为y,百位数字为z,由题意,得 解得 所以原数为 163.
7. 解:(1)由题意,得 解得
答:接收方收到的密码是 1,6,8.
(2)由题意,得 解得
答:发送方发出的密码是3,4,7.
专项点睛3 二元一次方程组与图表信息问题
1. 解:(1)设大正方形边长为 x cm,小正方形边长为y cm.
依题意得
解得
答:大正方形和小正方形的边长分别是 12 cm 和4 cm.
(2)设重叠部分的小正方形边长为 a cm,
依题意得3(4-a) +4=12,
解得
∴ 阴影面积
2. 解:(1)(37-31) ÷3=6÷3=2(cm);
(37-31)÷2=6÷2=3(cm).
故答案为2;3.
(2)设放入x个小球,y个大球,
由题意,得2x+3y=55-31,
又∵x,y均为正整数,
或 或
∴ 共有3 种放入方式.
方案1:放入3个小球,6个大球;
方案2:放入6个小球,4个大球;
方案3:放入9个小球,2个大球.
3. 解:(1)设1 辆 A 型车载满货物一次可运货x吨,1 辆B型车载满货物一次可运货y吨,
由题意,得
解得
答:1 辆A 型车载满货物一次可运货3 吨,1 辆B 型车载满货物一次可运货4 吨.
(2)依题意,得3a+4b=35,
又∵a,b均为自然数,
或 或
∴共有3 种租车方案,
方案1:租用A型车1辆,B型车8辆;
方案2:租用A 型车5 辆,B型车5辆;
方案3:租用A 型车9辆,B型车2 辆.
(3)选择方案 1 所需租车费为 1 ×200 + 8 ×240=2 120(元);
选择方案2所需租车费为5×200+5×240=2 200(元);选择方案3所需租车费为9×200+2×240=2280(元).
∵2 120<2 200<2 280,
∴最省钱的租车方案是方案 1:租用 A 型车 1 辆,B型车8 辆,最少的租车费为2 120 元.
第八章 培优精练
1. B 解析:由题意,可得方程组 解得
代入方程组
解得
解析:由题意,得方程组 由①可设a=2k,b=3k,c =4k,代入②得 2k+3k- 解得 故答案为
3. 145 解析:设打折前每盒肉粽的价格为x元,每盒白粽的价格为y元,
由题意,得 解得 所以5x+5y-(0.6×5x+0.7×5y)=5×50+5×30-(0.6×5×50 +0.7×5×30) =145.
4. 解:(1)原方程组变化为 解得 故原方程组的解为
(2)设x-y=A,x+y=B,原方程组变为 解得 即得方程组 解得
故原方程组的解为
由①+②+③,
得4x-4y+4z=8,
故x-y+z=2.④
由①-④,得3z=3,解得z=1.
由②+④,得5x=1,解得
把 代入④,得
故原方程组的解为
5. 解:由题意知, 是方程4x-by= -1 的解,所以把 代入方程4x-by= -1 中,解得 b=3.
如果乙将第一个方程中的b写成了它的相反数,那么第一个方程为4x+3y=-1,把 代入 4x+3y= -1,左边 = -10≠右边,故 不是4x+3y= -1 的解,所以乙应该是把第二个方程中的b看成了它的相反数,所以第二个方程错看为ax-3y=5,把 代入方程ax-3y=5,解得a=1.
所以a=1,b=3.
6. 解:(1)设生产竖式无盖纸盒 x个,横式无盖纸盒y个,
依据题意,得
解得
答:生产竖式无盖纸盒40个,横式无盖纸盒60个.
(2)设安排m名工人生产长方形纸板,则安排(78-m)名工人生产正方形纸板,
依据题意,得
解得 m=60,
∴78-m=78-60=18.
答:纸板车间应该安排60 名工人生产长方形纸板,
18 名工人生产正方形纸板.
中小学教育资源及组卷应用平台
8.1 二元一次方程组
1. (二元一次方程组的实际应用)《九章算术》是人类科学史上应用数学的“算经之首”,书中记载:今有三人共车,二车空;二人共车,九人步. 问:人与车各几何 译文:若3人坐一辆车,则两辆车是空的;若2人坐一辆车,则9人需要步行,问:人与车各多少 设有 x辆车,人数为y,根据题意可列方程组为 ( )
2.(二元一次方程组的解)写出一个唯一解为 的二元一次方程组是 .
3. (二元一次方程组的实际应用,图表信息题)根据图给出的信息,求每件 T 恤衫和每瓶矿泉水的价格(只列方程组).
4.(一元一次方程组的错解问题)小明在做家庭作业时发现练习册上一道解方程的题目被墨水污染, “□”和“△”表示被污染的内容,他翻开书后面的答案,这道题的解是 你能帮助他补上“□”和“△”的内容吗 写出你的方法.
5.(二元一次方程特殊解的实际应用)某同学去面包店买面包,面包有 A,B 两种包装,每个面包品质相同,且只能整盒购买,商品信息如下:
A包装盒 B 包装盒
每盒面包个数/个 3 8
每盒价格/元 5 11
若某同学正好买了50个面包,则他最少需要花多少元
8.2 消元——解二元一次方程组
1. (解二元一次方程组的方法)解方程组① 比较简便的方法是 ( )
A.都用代入法
B.都用加减法
C.①用代入法,②用加减法
D.①用加减法,②用代入法
2.(二元一次方程组的解)m为正整数,已知二元一次方程组 有整数解,则 的值为( )
A.3 或48 B.3
C.4 或49 D.48
3.(二元一次方程组的实际应用)如图,在长为15,宽为12 的长方形中,有形状、大小完全相同的5个小长方形,则图中阴影部分的面积为 ( )
A.35 B.45 C.55 D.65
4. (关于二元一次方程组的新定义型问题)对于实数x,y定义新运算x*y=ax +by+1,其a,b为常数,等式右边为通常的加法和乘法运算,若3*5=15,4*7=28,则5*9= .
5. (解二元一次方程组的)(2022·广东汕头澄海区期末)已知关于x,y 的二元一次方程组 的解为 那么关于 m,n的二元一次方程组 的解为 .
6.(解二元一次方程组)解下列方程组:
7.(解含参的二元一次方程组)已知关于a,b的二元一次方程组 ②且 abc≠0,求 的值.
8.3 实际问题与二元一次方程组
1. (计分问题)小方、小红和小军三人玩飞镖游戏,各投四支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小红的得分是 ( )
A.30分 B.32分
C.33 分 D.34分
2.(数字问题)一个两位数,它的个位数字是十位数字的2倍,且十位数字与个位数字和的3 倍比这个两位数小3,则这个两位数是 .
3.(古算问题)(2021·湖南邵阳中考)《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有共买物,人出八,盈三;人出七,不足四. 问人数、物价各几何 意思是:几个人一起去购买某物品,如果每人出8 钱,则多了3钱;如果每人出7钱,则少了4 钱.问有多少人,物品的价值是多少 该问题中物品的价值是 钱.
4.(行程问题)林芳沿公路匀速前进,每隔 4min就迎面开来一辆公共汽车,每隔6m in就有一辆公共汽车从背后超过她,假定公共汽车的速度不变,而且迎面开来的相邻两车的距离和从背后开来的相邻两车的距离都是1 200 m,求林芳的速度和公共汽车的速度.
5.(实际应用问题)“绿水青山就是金山银山”,科学研究表明:树叶在光合作用后产生的分泌物能够吸附空气中的悬浮颗粒物,具有滞尘净化空气的作用.已知一片银杏树叶一年的平均滞尘量比一片国槐树叶一年的平均滞尘量的2 倍少4m g,若一片国槐树叶与一片银杏树叶一年的平均滞尘总量为 62 mg.
(1)请分别求出一片国槐树叶和一片银杏树叶一年的平均滞尘量;
(2)娄底市双峰县九峰山森林公园某处有始于唐代的三棵银杏树,据估计三棵银杏树共有约50 000 片树叶.问这三棵银杏树一年的平均滞尘总量约多少千克.
6. (利润问题)某地区 2020年进出口总额为520 亿元,2021 年进出口总额比 2020 年有所增加,其中进口额增加了25% ,出口额增加了 30%.
注:进出口总额 =进口额 + 出口额.
(1)设 2020 年进口额为 x 亿元,出口额为y亿元,请用含x,y的代数式填表:
年份 进口额/亿元 出口额/ 亿元 进出口总额/亿元
2020 x y 520
2021 1.25x 1.3y
(2)已知 2021 年进出口总额比 2020 年增加了140亿元,求2021 年进口额和出口额分别是多少亿元
*8.4 三元一次方程组的解法
1. (三元一次方程组的求解)已知 x +4y-3z=0,且4x-5y+2z=0,则x:y:z为 ( )
A.1:2:3 B.1:3:2
C.2:1:3 D.3:1:2
2. (三元一次方程组的求解)若( ,则x+y+z等于( )
B. C.2 D. -2
3. (三元一次方程组的求解,同类项) 已知 与 是同类项,则x= ,y= ,z =
4.(三元一次方程组的实际应用)某中学举办的足球赛规定胜一场得3分,平一场得1分,负一场得0分,在这次足球赛中,八(1)班足球队共参加了8场比赛,其中平的场数是负的场数 的 2 倍,共得 17 分, 则该 队 负 了 场.
5. (三元一次方程组的求解) 给定 方程组
口果令 则
方程组 由此解得 对不对 为什么
6. (三元一次方程组的应用,数字问题)有一个三位数,个位数字是百位数字的3 倍,十位数字比百位数字大5,若将此数的个位数与百位数互相对调,所得新数比原数的2 倍多35,求原数.
7.(三元一次方程组的实际应用)为确保信息安全,在传输时往往需加密,发送方发出一组密码a,b,c时,接收方对应收到的密码为A,B,C.双方约定:A=2a-b,B=2b,C=b+c,例如:发出1,2,3,则收到0,4,5.
(1)当发送方发出一组密码为2,3,5时,接收方收到的密码是多少
(2)当接收方收到一组密码为2,8,11 时,发送方发出的密码是多少
专项点睛3 二元一次方程组与图表信息问题
1学校举办“艺术周”创意设计展览,如图,现有一个大正方形和四个一样的小正方形,小明、小聪、小方分别用这些正方形设计出了图①,图②,图③三种图案:
(1)根据图①,图②中所标数据,求出大正方形和小正方形的边长分别是多少厘米
(2)图③中四个小正方形的重叠部分也是三个一样的小正方形,求阴影部分的面积.
2. 根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高 cm,放入 个大球水面升高 cm
(2)如果同时放入大、小两种球,使水面上升到55 cm,列出放入大球、小球个数的关系式,并写出所有可能情况.
3.已知 A型车和 B 型车载满货物一次可运货情况如下表:
A型车/辆 B型车/辆 共运货/吨
3 2 17
2 3 18
某物流公司现有35 吨货物,计划同时租用A型车 a 辆,B 型车b 辆,一次运完,且恰好每辆车都载满货物. 根据以上信息,解答下列问题:
(1)1 辆 A 型车和1 辆 B 型车都载满货物一次可分别运货多少吨
(2)请你帮该物流公司设计租车方案;
(3)若 A 型车每辆的租金为 200 元/次,B 型车每辆的租金为240 元/次,请选出最省钱的租车方案,并求出最少的租车费.
第八章 培优精练
1.(二元一次方程组的同解问题)若方程组 と、 有相同的解,则a,b的值为( )
A.2,3 B.3,2 C.2, -1 D. -1,2
2.(三元一次方程组的求解)已知 且 则a = ,b= ,c = .
3.(二元一次方程组的实际应用)端午节是中国传统节日,人们有吃粽子的习俗. 某商场从6 月 12 日起开始打折促销,肉粽六折,白粽七折,打折前购买4 盒肉粽和5 盒白粽需350元,打折后购买5盒肉粽和10 盒白粽需 360 元. 轩轩同学想为敬老院送肉粽和白粽各5盒,则他在6月13 日购买的花费比在打折前购买节省 元.
4.(二元一次方程组的求解)解下列方程组:
5.(二元一次方程组的错解问题)甲、乙两人解方 程 组 甲 因 看 错 a, 解得 乙将其中一个方程的b写成了它的相反数,解得 求 a,b 的值.
6.(二元一次方程组的实际应用)某工厂生产如图①所示的长方形和正方形纸板,做成如图②所示的竖式与横式两种长方体形状的无盖纸盒,其中竖式纸盒由4个长方形和1个正方形纸板做成,横式纸盒由 3 个长方形和2 个正方形纸板做成(给定的长方形和正方形纸板都不用裁剪,也不考虑接缝).
(1)现有长方形纸板340 张,正方形纸板160张,做成上述两种纸盒,纸板恰好用完,求两种纸盒的生产个数.
(2)纸板车间共有78 名工人,每个工人一天能生产 70 张长方形纸板或者 100 张正方形纸板,已知一个竖式纸盒与一个横式纸盒配套,要求纸板车间一天生产的纸板由其他车间做成竖式纸盒与横式纸盒配套,问纸板车间应该如何安排工人生产两种纸板
第八章 二元一次方程组
8.1 二元一次方程组
1. B
(答案不唯一)
解析:因为x=1,y=2,
所以2x+y=4,3x-2y= -1.
故 有唯一的解是
3. 解:设每件T 恤衫x元,每瓶矿泉水y元.
由题意得
4. 解:因为方程组的解为 所以把 分别代入方程组的每一个方程,得□=3×2 -2×( -1) =6+2=8,△=5×2+( -1) =10-1=9.
5. 解:设购买 A 包装面包x盒,B包装面包y盒.
由题意得3x+8y=50.
∵x,y为非负整数或
当x=6,y=4时,费用为5×6+11×4=74(元);
当x=14,y=1时,费用为5×14+11×1 =81(元).
∵74<81,
∴某同学正好买了 50 个面包,则他最少需要花74 元.
8.2 消元———解二元一次方程组
1. C 解析:①中的第一个方程为y=x-3,用代入法比较简便;②中的x的系数相等,用加减法比较简便.故选 C.
2. B 解析:
①+②,得(m+3)x=10,解得
把 代入②,得
由方程组有整数解,得m+3= ±1,m+3= ±5,
解得m = -2,-4,2,-8.
由m为正整数,得m=2,
则 故选 B.
3. B 解析:设小长方形的长为x,宽为 y.
根据题意,得 解得
所以
4.41 解析:由题意知,若3*5=15,4*7=28,则 解得 所以5*9= -37×5+25×9+1 =41.
解析:∵ 关于 x,y 的二元一次方程组 的解为
∴ 可 以 把 关 于 m, n 的 二 元 一 次 方 程 组 中的(m+n)看成x,(m-n)看成y,
解得
6. 解:(1)原方程组整理可得
①-②,得4y= -28,解得y= -7.
将y= -7代入①,得3x+7= -8.
解得x= -5.
故原方程组的解为
(2)原方程组整理得
①×2+②,得5x=10,解得x=2.
把x=2代入①,得2-y=-1.
解得y=3.
故原方程组的解为
(3)设 则 x =3k,y=4k. 把 x =3k,y =4k代入x+2y=11,得3k+2×4k=11,解得k=1,即x=3k=3,y=4k=4,所以原方程组的解为
7. 解:①+②,得3a-b= -5c.③
②-①,得a-5b= -11c.④
④×2,得2a-10b= -22c.⑤
将③和⑤代)入
得
8.3 实际问题与二元一次方程组
1. B 解析:设掷中 A 区、B区一次的得分分别为x分,y分.
依据题意,得 解得
所以小红的得分是5+3×9=32(分).
2. 12 解析:设个位数字为x,十位数字为y. 由题意,得 解得 则这个两位数是 12.
3.53 解析:设有x人,物品的价值为y钱. 依据题意,得 解得 即该问题中物品的价值是 53 钱.
4. 解:设林芳的速度为 x m/min,公共汽车的速度为y m/min.
由题意,得 解得
答:林芳的速度为 50 m/min,公共汽车的速度为250 m/min.
5. 解:(1)设一片银杏树叶一年的平均滞尘量为 x mg,一片国槐树叶一年的平均滞尘量为y mg.
由题意得
解得
答:一片银杏树叶一年的平均滞尘量为40 mg,一片国槐树叶一年的平均滞尘量为22 mg.
(2)50 000×40=2000 000(mg) =2kg.
答:这三棵银杏树一年的平均滞尘总量约为2k g.
6. 解:(1)1.25x+1.3y
(2)由题意得 解得
∴ 1.25x=400,1.3y=260.
答:2021 年进口额是400亿元,出口额是260 亿元.
*8.4 三元一次方程组的解法
1. A 解析:组成方程组 と①×5+②×4,得21x=7z,解得 代入①得 则
2. A 解析:∵ 解得 则
3.6;8;3 解析:由题意,得
由①+②,得2y=16,解得y=8.
由①+③,得2x=12,解得x=6.
由②+③,得2z=6,解得z=3.
4. 1 解析:设八(1)班足球队胜了x场,平了y场,负了z场,由题意,得 解得 即八(1)班足球队负了1场.
5. 解:不对.
理由:方程组
由①+②+③,得2(A+B+C)=8.
所以A+B+C=4.④
由④-①,得C=3.
由④-②,得A=2.
由④-③,得B= -1.
即
由此可见题目中给出的答案不对.
6. 解:设个位数字为x,十位数字为y,百位数字为z,由题意,得 解得 所以原数为 163.
7. 解:(1)由题意,得 解得
答:接收方收到的密码是 1,6,8.
(2)由题意,得 解得
答:发送方发出的密码是3,4,7.
专项点睛3 二元一次方程组与图表信息问题
1. 解:(1)设大正方形边长为 x cm,小正方形边长为y cm.
依题意得
解得
答:大正方形和小正方形的边长分别是 12 cm 和4 cm.
(2)设重叠部分的小正方形边长为 a cm,
依题意得3(4-a) +4=12,
解得
∴ 阴影面积
2. 解:(1)(37-31) ÷3=6÷3=2(cm);
(37-31)÷2=6÷2=3(cm).
故答案为2;3.
(2)设放入x个小球,y个大球,
由题意,得2x+3y=55-31,
又∵x,y均为正整数,
或 或
∴ 共有3 种放入方式.
方案1:放入3个小球,6个大球;
方案2:放入6个小球,4个大球;
方案3:放入9个小球,2个大球.
3. 解:(1)设1 辆 A 型车载满货物一次可运货x吨,1 辆B型车载满货物一次可运货y吨,
由题意,得
解得
答:1 辆A 型车载满货物一次可运货3 吨,1 辆B 型车载满货物一次可运货4 吨.
(2)依题意,得3a+4b=35,
又∵a,b均为自然数,
或 或
∴共有3 种租车方案,
方案1:租用A型车1辆,B型车8辆;
方案2:租用A 型车5 辆,B型车5辆;
方案3:租用A 型车9辆,B型车2 辆.
(3)选择方案 1 所需租车费为 1 ×200 + 8 ×240=2 120(元);
选择方案2所需租车费为5×200+5×240=2 200(元);选择方案3所需租车费为9×200+2×240=2280(元).
∵2 120<2 200<2 280,
∴最省钱的租车方案是方案 1:租用 A 型车 1 辆,B型车8 辆,最少的租车费为2 120 元.
第八章 培优精练
1. B 解析:由题意,可得方程组 解得
代入方程组
解得
解析:由题意,得方程组 由①可设a=2k,b=3k,c =4k,代入②得 2k+3k- 解得 故答案为
3. 145 解析:设打折前每盒肉粽的价格为x元,每盒白粽的价格为y元,
由题意,得 解得 所以5x+5y-(0.6×5x+0.7×5y)=5×50+5×30-(0.6×5×50 +0.7×5×30) =145.
4. 解:(1)原方程组变化为 解得 故原方程组的解为
(2)设x-y=A,x+y=B,原方程组变为 解得 即得方程组 解得
故原方程组的解为
由①+②+③,
得4x-4y+4z=8,
故x-y+z=2.④
由①-④,得3z=3,解得z=1.
由②+④,得5x=1,解得
把 代入④,得
故原方程组的解为
5. 解:由题意知, 是方程4x-by= -1 的解,所以把 代入方程4x-by= -1 中,解得 b=3.
如果乙将第一个方程中的b写成了它的相反数,那么第一个方程为4x+3y=-1,把 代入 4x+3y= -1,左边 = -10≠右边,故 不是4x+3y= -1 的解,所以乙应该是把第二个方程中的b看成了它的相反数,所以第二个方程错看为ax-3y=5,把 代入方程ax-3y=5,解得a=1.
所以a=1,b=3.
6. 解:(1)设生产竖式无盖纸盒 x个,横式无盖纸盒y个,
依据题意,得
解得
答:生产竖式无盖纸盒40个,横式无盖纸盒60个.
(2)设安排m名工人生产长方形纸板,则安排(78-m)名工人生产正方形纸板,
依据题意,得
解得 m=60,
∴78-m=78-60=18.
答:纸板车间应该安排60 名工人生产长方形纸板,
18 名工人生产正方形纸板.
