6.1.3向量的减法、6.1.4向量的数乘 课件(共21张PPT)
文档属性
| 名称 | 6.1.3向量的减法、6.1.4向量的数乘 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 456.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-29 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
6.1.3向量的减法、6.1.4向量的数乘
(1)本节将要研究哪类问题?
(2)本节要研究的对象在高中的地位是怎样的?
问题1 阅读教材相应内容,思考下列问题:
整体概览
(1)本节主要研究向量的减法和数乘运算.
(2)通过第一节向量的概念及第二节向量加法的学习,认识了解向量,本节延续上一节的学习要求,开始向量的减法运算,数乘运算.
新知探究
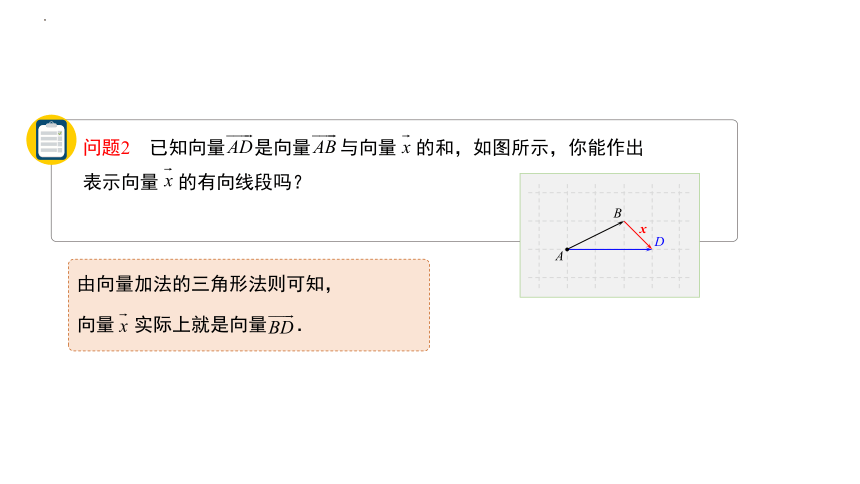
问题2 已知向量 是向量 与向量 的和,如图所示,你能作出表示向量 的有向线段吗?
由向量加法的三角形法则可知,
A
B
D
x
向量 实际上就是向量 .
新知探究
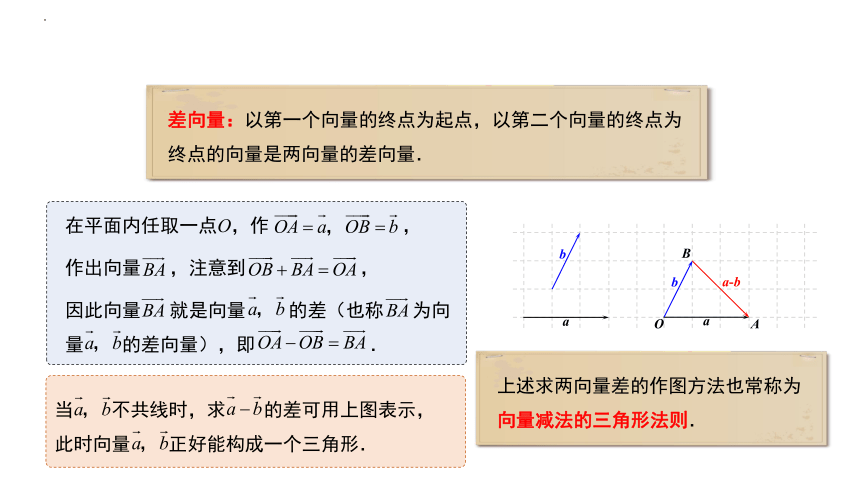
差向量:以第一个向量的终点为起点,以第二个向量的终点为终点的向量是两向量的差向量.
在平面内任取一点O,作 ,
a
b
作出向量 ,注意到 ,
因此向量 就是向量 的差(也称 为向量 的差向量),即 .
当 不共线时,求 的差可用上图表示,此时向量 正好能构成一个三角形.
O
A
a
B
b
a-b
上述求两向量差的作图方法也常称为向量减法的三角形法则.
新知探究
相反向量:给定一个向量,我们把与这个向量方向相反、大小相等的向量称为它的相反向量.
向量 的相反向量记作- .
因此, 的相反向量是- ,而且- = .
因为零向量的始点与终点相同,所以- = .
注意:(1)任何一个向量与它的相反向量的和都等于零向量.即
(2)一个向量减去另一个向量,等于第一个向量加上第二个向量的相反向量.
新知探究
例1
已知平行四边形ABCD中, , ,
用 , 分别表示向量 , .
解:由向量加法的平行四边形可知,
由减法的定义可知
新知探究
例2
已知| |=1,| |=2,
求 的取值范围.
解:当 , 不共线时,
正好是一个三角形的三条边,
从而
因此1< <3;
综上有1≤ ≤3.
当 , 共线时,
如果 与 方向相同,有
如果 , 方向相反,有
新知探究
问题3 结果是向量吗?如果是,那么结果向量的模是多少?方向如何?与向量 的模及方向有什么关系?可否类比实数乘法的定义方法(5+5+5可以表示为3×5),把 进行简写?
我们已经知道,多个向量相加,结果是一个向量.
特别地,给定一个向量 ,3个 相加 的结果,是一个模为3| |、方向与 相同的向量,通常这个向量简单记作3 .
新知探究
问题4 你能根据上述实例,给出实数λ与任意一个向量 的乘积λ 的定义吗?
一般地,给定一个实数λ与任意一个向量 ,规定它们的乘积是一个向量,记作 ,其中
(1)当λ≠0且 ≠0时, 的模为λ| |,而且λ 的方向如下:
①当λ>0时,与 的方向相同
②当λ<0时,与 的方向相反
(2)当λ=0或 =0时,λ =0
实数λ与向量 相乘的运算简称为数乘向量.
新知探究
数乘向量的几何意义是,把向量沿着它的方向或反方向放大或缩小.
数乘向量的结果是一个向量,而且这个向量与原来的向量共线(平行),即λ ∥ ;
特别地,一个向量的相反向量可以看成-1与这个向量的乘积,即- =(-1) .
①(λ+μ)a=λa+μa;
②λ(μa)=(λμ)a;
③λ(a+b)=λa+λb.
数乘向量的定义说明,如果存在实数λ,使得 =λ ,则 ∥ .
新知探究
例3
已知 , ,其中 为非零向量,判断 、 是否平行,
并求| |∶| |的值.
解:
由 ,得 ,代入 ,得 ,
因此 ∥ ,且| |∶| |=3∶2
新知探究
例4
已知 , ,判断A,B,C是否共线,如果共线,
求出AB∶AC.
解:
由已知得 ,因此A,B,C三点共线,
且AC=5AB,即AB∶AC=1∶5
巩固练习
练习1
下列各式中不表示向量的是( )
A.0·a B.a+3b
C.|3a| D. e(x,y∈R,且x≠y)
C
解析:向量的数乘运算结果仍为向量,显然只有|3a|不是向量.
巩固练习
练习2
4(a-b)-3(a+b)-b等于( )
A.a-2b B.a
C.a-6b D.a-8b
D
解析:4(a-b)-3(a+b)-b=4a-4b-3a-3b-b
=a-8b.
归纳小结
问题5 (1)向量减法的三角形法则是什么?
O
A
B
a
b
a
b
a-b
在平面内任取一点O,作 ,作出向量 ,注意到 ,因此向量 就是向量 的差(也称 为向量 的差向量),
即 ,当 不共线时,
求 的差可用右图表示,此时向量
正好能构成一个三角形.
归纳小结
问题5 (2)什么是数乘向量?
一般地,给定一个实数λ与任意一个向量 ,规定它们的乘积是一个向量,记作 ,其中
(1)当λ≠0且 ≠0时, 的模为λ| |,而且λ 的方向如下:
①当λ>0时,与 的方向相同
②当λ<0时,与 的方向相反
(2)当λ=0或 =0时,λ =0
实数λ与向量 相乘的运算简称为数乘向量.
作业布置
作业:教科书练习A:1,2,3题.
目标检测
测试1
若两个非零向量a与(2x-1)a方向相同,则x的取值范围为________.
x>
解析:由定义可知,2x-1>0,即x> .
目标检测
测试2
O为平行四边形ABCD的中心, =4e1, =6e2,则3e2-2e1=____________.
(或 )
解析:设点E为平行四边形ABCD的边BC的中点,点F为AB边中点,
则3e2-2e1= + = = .
目标检测
测试3
若平面内不共线的四点O,A,B,C满足 = + ,则 =________.
2
解析:
①÷②得 =2.
因为 = + ,
所以 - = + - ,
即 = ,
所以| |= | |, ①
同理可得| |= | |, ②
6.1.3向量的减法、6.1.4向量的数乘
(1)本节将要研究哪类问题?
(2)本节要研究的对象在高中的地位是怎样的?
问题1 阅读教材相应内容,思考下列问题:
整体概览
(1)本节主要研究向量的减法和数乘运算.
(2)通过第一节向量的概念及第二节向量加法的学习,认识了解向量,本节延续上一节的学习要求,开始向量的减法运算,数乘运算.
新知探究
问题2 已知向量 是向量 与向量 的和,如图所示,你能作出表示向量 的有向线段吗?
由向量加法的三角形法则可知,
A
B
D
x
向量 实际上就是向量 .
新知探究
差向量:以第一个向量的终点为起点,以第二个向量的终点为终点的向量是两向量的差向量.
在平面内任取一点O,作 ,
a
b
作出向量 ,注意到 ,
因此向量 就是向量 的差(也称 为向量 的差向量),即 .
当 不共线时,求 的差可用上图表示,此时向量 正好能构成一个三角形.
O
A
a
B
b
a-b
上述求两向量差的作图方法也常称为向量减法的三角形法则.
新知探究
相反向量:给定一个向量,我们把与这个向量方向相反、大小相等的向量称为它的相反向量.
向量 的相反向量记作- .
因此, 的相反向量是- ,而且- = .
因为零向量的始点与终点相同,所以- = .
注意:(1)任何一个向量与它的相反向量的和都等于零向量.即
(2)一个向量减去另一个向量,等于第一个向量加上第二个向量的相反向量.
新知探究
例1
已知平行四边形ABCD中, , ,
用 , 分别表示向量 , .
解:由向量加法的平行四边形可知,
由减法的定义可知
新知探究
例2
已知| |=1,| |=2,
求 的取值范围.
解:当 , 不共线时,
正好是一个三角形的三条边,
从而
因此1< <3;
综上有1≤ ≤3.
当 , 共线时,
如果 与 方向相同,有
如果 , 方向相反,有
新知探究
问题3 结果是向量吗?如果是,那么结果向量的模是多少?方向如何?与向量 的模及方向有什么关系?可否类比实数乘法的定义方法(5+5+5可以表示为3×5),把 进行简写?
我们已经知道,多个向量相加,结果是一个向量.
特别地,给定一个向量 ,3个 相加 的结果,是一个模为3| |、方向与 相同的向量,通常这个向量简单记作3 .
新知探究
问题4 你能根据上述实例,给出实数λ与任意一个向量 的乘积λ 的定义吗?
一般地,给定一个实数λ与任意一个向量 ,规定它们的乘积是一个向量,记作 ,其中
(1)当λ≠0且 ≠0时, 的模为λ| |,而且λ 的方向如下:
①当λ>0时,与 的方向相同
②当λ<0时,与 的方向相反
(2)当λ=0或 =0时,λ =0
实数λ与向量 相乘的运算简称为数乘向量.
新知探究
数乘向量的几何意义是,把向量沿着它的方向或反方向放大或缩小.
数乘向量的结果是一个向量,而且这个向量与原来的向量共线(平行),即λ ∥ ;
特别地,一个向量的相反向量可以看成-1与这个向量的乘积,即- =(-1) .
①(λ+μ)a=λa+μa;
②λ(μa)=(λμ)a;
③λ(a+b)=λa+λb.
数乘向量的定义说明,如果存在实数λ,使得 =λ ,则 ∥ .
新知探究
例3
已知 , ,其中 为非零向量,判断 、 是否平行,
并求| |∶| |的值.
解:
由 ,得 ,代入 ,得 ,
因此 ∥ ,且| |∶| |=3∶2
新知探究
例4
已知 , ,判断A,B,C是否共线,如果共线,
求出AB∶AC.
解:
由已知得 ,因此A,B,C三点共线,
且AC=5AB,即AB∶AC=1∶5
巩固练习
练习1
下列各式中不表示向量的是( )
A.0·a B.a+3b
C.|3a| D. e(x,y∈R,且x≠y)
C
解析:向量的数乘运算结果仍为向量,显然只有|3a|不是向量.
巩固练习
练习2
4(a-b)-3(a+b)-b等于( )
A.a-2b B.a
C.a-6b D.a-8b
D
解析:4(a-b)-3(a+b)-b=4a-4b-3a-3b-b
=a-8b.
归纳小结
问题5 (1)向量减法的三角形法则是什么?
O
A
B
a
b
a
b
a-b
在平面内任取一点O,作 ,作出向量 ,注意到 ,因此向量 就是向量 的差(也称 为向量 的差向量),
即 ,当 不共线时,
求 的差可用右图表示,此时向量
正好能构成一个三角形.
归纳小结
问题5 (2)什么是数乘向量?
一般地,给定一个实数λ与任意一个向量 ,规定它们的乘积是一个向量,记作 ,其中
(1)当λ≠0且 ≠0时, 的模为λ| |,而且λ 的方向如下:
①当λ>0时,与 的方向相同
②当λ<0时,与 的方向相反
(2)当λ=0或 =0时,λ =0
实数λ与向量 相乘的运算简称为数乘向量.
作业布置
作业:教科书练习A:1,2,3题.
目标检测
测试1
若两个非零向量a与(2x-1)a方向相同,则x的取值范围为________.
x>
解析:由定义可知,2x-1>0,即x> .
目标检测
测试2
O为平行四边形ABCD的中心, =4e1, =6e2,则3e2-2e1=____________.
(或 )
解析:设点E为平行四边形ABCD的边BC的中点,点F为AB边中点,
则3e2-2e1= + = = .
目标检测
测试3
若平面内不共线的四点O,A,B,C满足 = + ,则 =________.
2
解析:
①÷②得 =2.
因为 = + ,
所以 - = + - ,
即 = ,
所以| |= | |, ①
同理可得| |= | |, ②
