第六章 特殊平行四边形 1 菱形的性质与判定 第3课时 菱形的性质与判定的应用(含答案)
文档属性
| 名称 | 第六章 特殊平行四边形 1 菱形的性质与判定 第3课时 菱形的性质与判定的应用(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-29 09:15:32 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第六章 特殊平行四边形
1 菱形的性质与判定
第3课时 菱形的性质与判定的应用
基 础 练
练点 菱形的性质与判定的应用
1.如图,在菱形 ABCD 中,对角线 AC,BD 分别为 16 和 12, 于点E,则 DE 的长是( )
C.10 D.8
(第1题) (第2题)
2.如图,两张等宽的纸条交叉叠放在一起,重合部分构成一个四边形ABCD,在其中一张纸条转动的过程中,下列结论一定成立的是( )
B.四边形ABCD的面积不变
D.四边形 ABCD的周长不变
3.如图,四边形ABCD 是菱形,E,F 是对角线AC 上的两点,且 连接 BF,FD,DE,EB.求证:四边形 DEBF 是菱形.
提 升 练
4.如图,在中,用直尺和圆规作 的平分线交BC 于点E,连接 EF.
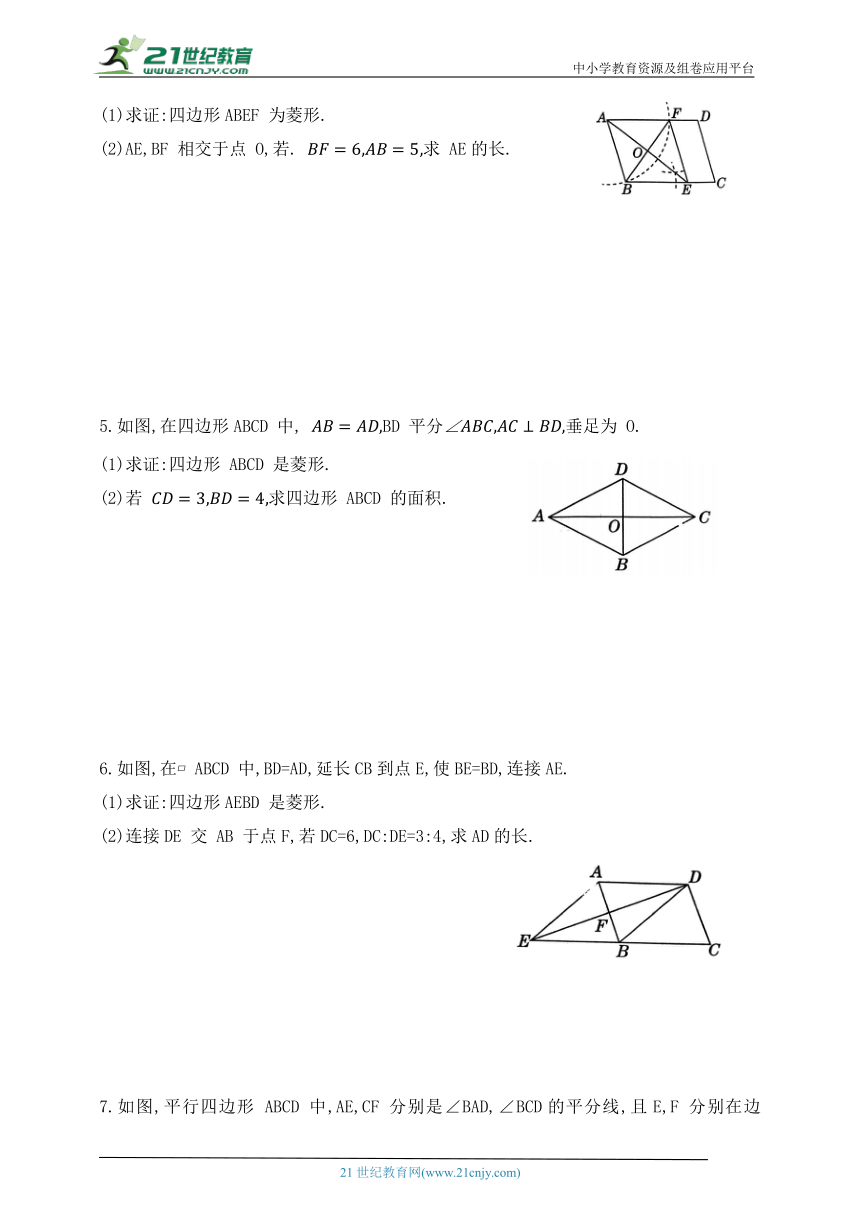
(1)求证:四边形ABEF 为菱形.
(2)AE,BF 相交于点 O,若. 求 AE的长.
5.如图,在四边形ABCD 中, BD 平分垂足为 O.
(1)求证:四边形 ABCD 是菱形.
(2)若 求四边形 ABCD 的面积.
6.如图,在 ABCD 中,BD=AD,延长CB到点E,使BE=BD,连接AE.
(1)求证:四边形AEBD 是菱形.
(2)连接DE 交 AB 于点F,若DC=6,DC:DE=3:4,求AD的长.
7.如图,平行四边形 ABCD 中,AE,CF 分别是∠BAD,∠BCD的平分线,且E,F 分别在边 BC,AD 上,AE=AF.
(1)求证:四边形AECF 是菱形.
(2)若∠ABC=60°,AB =4,求平行线 AB 与DC间的距离.
8.如图,在四边形 ABCD 中,AB∥CD,AC 平分∠DAB,AB=2CD,E为AB的中点,连接CE.
(1)求证:四边形AECD 是菱形.
(2)若∠D=120°,CD=2,求△ABC的面积.
9.如图,在四边形ABCD 中, ∥对角线 AC, BD 交于点O,AC 平分 过点 C 作AB 交 AB 的延长线于点 E,连接OE.
(1)求证:四边形 ABCD 是菱形.
(2)若 求OE 的长.
10. 如图,在四边形 ABCD 中, ∥
(1)求证:
(2)若E,F,G,H 分别是AB,CD,AC,BD 的中点,求证:线段EF 与线段GH 互相垂直平分.
参考答案
1. A 【点拨】设 AC 与BD的交点为 O,∵ 四边形AB-CD 是菱形,
2. A 【点拨】设两张等宽的纸条的宽为h,∵ 纸条的对边平行,∴AD∥BC,AB∥DC,
∴ 四边形ABCD 是平行四边形.
∴ AD = CD.
3.【证明】∵四边形ABCD 是菱形,AD,∠DAB = ∠DCB,AC 平分CA平分
△DCF(SAS),∴DE = BE = BF = DF,
∴ 四边形DEBF 是菱形.
4.(1)【证明】由作图可知.
∵四边形 ABCD 是平行四边形, ∥
∴ BE=FA,∴四边形ABEF 为平行四边形.
∵AB=AF,∴四边形ABEF 为菱形.
(2)【解】∵ 四边形ABEF为菱形,∴AE⊥BF,BO=
在 Rt△AOB 中, 4,∴ AE=2AO=8.
5.(1)【证明】∵AB =AD,∴ ∠ABD=∠ADB.
∵BD 平分∠ABC,∴∠ABD =∠CBD,∴ ∠ADB =∠CBD.
∵AB=AD,AC⊥BD,∴BO=DO.
在△AOD与△COB中 ∴ △AOD≌△COB,∴ AO=OC,
∴ 四边形ABCD 是平行四边形.
∵ AC⊥BD,∴ 四边形ABCD是菱形.
(2)【解】
∵
6.(1)【证明】∵ 四边形ABCD是平行四边形,∴AD∥BC,∴ AD∥BE.
∵ BD=AD,BE = BD,∴ AD = BE, ∴四边形AEBD 是平行四边形.
又∵ BD=AD,∴ 四边形AEBD 是菱形.
(2)【解】∵ 四边形ABCD是平行四边形,
∵四边形AEBD 是菱形,∴
7.(1)【证明】∵四边形ABCD 是平行四边形,∴∠BAD=∠BCD,AD∥BC.
∵AE,CF 分别是∠BAD,∠BCD的平分线,
∴
∥∴∠DAE=∠AEB,∴ ∠BCF =∠AEB,∴ AE∥FC,∴四边形 AECF 是平行四边形. ∵ AE=AF,∴ 四边形AECF 是菱形.
(2)【解】连接AC,由(1)知∠DAE=∠AEB,∠BAE=∠DAE,∴ ∠BAE=∠AEB,∴ AB =EB.
∵∠ABC=60°,∴△ABE 是等边三角形,∴∠BAE=∠AEB=60°,AB =AE =EB =4.
由(1)知四边形AECF 是菱形,∴AE=CE =4,∴ ∠EAC=∠ECA.
∵ ∠AEB 是△AEC的一个外角,∴∠AEB =∠EAC +∠ECA=60°,∴∠EAC=∠ECA =30°,∴∠BAC =∠BAE +∠EAC = 90°,由勾股定理得 即平行线 AB 与DC 间的距离是
8.(1)【证明】∵ E 为 AB 的中点,∴ AB =2AE.
又∵AB=2CD,∴CD=AE.又∵AB∥CD,即AE∥CD,∴四边形AECD 是平行四边形.
∵ AC平分∠DAB,∴∠DAC=∠EAC.∵ AB∥CD,∴ ∠DCA=∠EAC.∴∠DCA =∠DAC.
∴ AD= CD. ∴ 四边形AECD 是菱形.
(2)【解】∵ 四边形 AECD 是菱形,CD =2,∠D=120°,
∴CE=AE =CD=2,AB =2CD=4,∠AEC=∠D = 120°.
∴ AE = BE = CE =2,∠CEB = 60°,∠CAE= ∠ACE =30°.
∴ △CEB 是等边三角形.∴BC=CE =2,∠BCE=60°.∴∠ACB =∠BCE +∠ACE=90°.
在 Rt△ABC 中,
9.(1)【证明】∵AC 平分∠BAD,∴∠DAC=∠BAC.
在△ADC 和△ABC中, ∴△ADC≌△ABC,∴AD=AB,CD=CB.
∵AB∥CD,∴∠DCA=∠BAC,∴ ∠DAC=∠DCA,∴AD=CD,
∴AD=AB=CD=CB,∴ 四边形ABCD 是菱形.
(2)【解】∵ 四边形ABCD 是菱形,BD=2,∴AC⊥
延长EO到点F,使OF=EO,连接AF.
∵AO=CO,∠AOF=∠COE,∴ △AOF≌△COE,∴ AF =CE,∠F=∠CEO,∴AF∥CE,
∴∠FAE+∠CEA=180°.
∵ CE⊥AB,∴ ∠AEC = 90°,∴ ∠EAF =∠AEC=90°.
又∵ AE = EA,∴ △AEC ≌△EAF,
10.【证明】(1)如图,过点 B 作BM∥AC 交 DC 的延长线于点M,则∠ACD =∠M.
∵ AB∥CD,∴ 四边形ABMC 为平行四边形.
又
又∵
(2)如图,连接 EH,HF,FG,GE.
∵ E,F,G,H 分别是AB,CD,AC,BD 的中点,
∥且 ∥且 ∥FG,HE = FG.
∴ 四边形 HFGE 为平行四边形.
由(1)知, 为菱形.
∴线段 EF 与线段 GH 互相垂直平分.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 特殊平行四边形
1 菱形的性质与判定
第3课时 菱形的性质与判定的应用
基 础 练
练点 菱形的性质与判定的应用
1.如图,在菱形 ABCD 中,对角线 AC,BD 分别为 16 和 12, 于点E,则 DE 的长是( )
C.10 D.8
(第1题) (第2题)
2.如图,两张等宽的纸条交叉叠放在一起,重合部分构成一个四边形ABCD,在其中一张纸条转动的过程中,下列结论一定成立的是( )
B.四边形ABCD的面积不变
D.四边形 ABCD的周长不变
3.如图,四边形ABCD 是菱形,E,F 是对角线AC 上的两点,且 连接 BF,FD,DE,EB.求证:四边形 DEBF 是菱形.
提 升 练
4.如图,在中,用直尺和圆规作 的平分线交BC 于点E,连接 EF.
(1)求证:四边形ABEF 为菱形.
(2)AE,BF 相交于点 O,若. 求 AE的长.
5.如图,在四边形ABCD 中, BD 平分垂足为 O.
(1)求证:四边形 ABCD 是菱形.
(2)若 求四边形 ABCD 的面积.
6.如图,在 ABCD 中,BD=AD,延长CB到点E,使BE=BD,连接AE.
(1)求证:四边形AEBD 是菱形.
(2)连接DE 交 AB 于点F,若DC=6,DC:DE=3:4,求AD的长.
7.如图,平行四边形 ABCD 中,AE,CF 分别是∠BAD,∠BCD的平分线,且E,F 分别在边 BC,AD 上,AE=AF.
(1)求证:四边形AECF 是菱形.
(2)若∠ABC=60°,AB =4,求平行线 AB 与DC间的距离.
8.如图,在四边形 ABCD 中,AB∥CD,AC 平分∠DAB,AB=2CD,E为AB的中点,连接CE.
(1)求证:四边形AECD 是菱形.
(2)若∠D=120°,CD=2,求△ABC的面积.
9.如图,在四边形ABCD 中, ∥对角线 AC, BD 交于点O,AC 平分 过点 C 作AB 交 AB 的延长线于点 E,连接OE.
(1)求证:四边形 ABCD 是菱形.
(2)若 求OE 的长.
10. 如图,在四边形 ABCD 中, ∥
(1)求证:
(2)若E,F,G,H 分别是AB,CD,AC,BD 的中点,求证:线段EF 与线段GH 互相垂直平分.
参考答案
1. A 【点拨】设 AC 与BD的交点为 O,∵ 四边形AB-CD 是菱形,
2. A 【点拨】设两张等宽的纸条的宽为h,∵ 纸条的对边平行,∴AD∥BC,AB∥DC,
∴ 四边形ABCD 是平行四边形.
∴ AD = CD.
3.【证明】∵四边形ABCD 是菱形,AD,∠DAB = ∠DCB,AC 平分CA平分
△DCF(SAS),∴DE = BE = BF = DF,
∴ 四边形DEBF 是菱形.
4.(1)【证明】由作图可知.
∵四边形 ABCD 是平行四边形, ∥
∴ BE=FA,∴四边形ABEF 为平行四边形.
∵AB=AF,∴四边形ABEF 为菱形.
(2)【解】∵ 四边形ABEF为菱形,∴AE⊥BF,BO=
在 Rt△AOB 中, 4,∴ AE=2AO=8.
5.(1)【证明】∵AB =AD,∴ ∠ABD=∠ADB.
∵BD 平分∠ABC,∴∠ABD =∠CBD,∴ ∠ADB =∠CBD.
∵AB=AD,AC⊥BD,∴BO=DO.
在△AOD与△COB中 ∴ △AOD≌△COB,∴ AO=OC,
∴ 四边形ABCD 是平行四边形.
∵ AC⊥BD,∴ 四边形ABCD是菱形.
(2)【解】
∵
6.(1)【证明】∵ 四边形ABCD是平行四边形,∴AD∥BC,∴ AD∥BE.
∵ BD=AD,BE = BD,∴ AD = BE, ∴四边形AEBD 是平行四边形.
又∵ BD=AD,∴ 四边形AEBD 是菱形.
(2)【解】∵ 四边形ABCD是平行四边形,
∵四边形AEBD 是菱形,∴
7.(1)【证明】∵四边形ABCD 是平行四边形,∴∠BAD=∠BCD,AD∥BC.
∵AE,CF 分别是∠BAD,∠BCD的平分线,
∴
∥∴∠DAE=∠AEB,∴ ∠BCF =∠AEB,∴ AE∥FC,∴四边形 AECF 是平行四边形. ∵ AE=AF,∴ 四边形AECF 是菱形.
(2)【解】连接AC,由(1)知∠DAE=∠AEB,∠BAE=∠DAE,∴ ∠BAE=∠AEB,∴ AB =EB.
∵∠ABC=60°,∴△ABE 是等边三角形,∴∠BAE=∠AEB=60°,AB =AE =EB =4.
由(1)知四边形AECF 是菱形,∴AE=CE =4,∴ ∠EAC=∠ECA.
∵ ∠AEB 是△AEC的一个外角,∴∠AEB =∠EAC +∠ECA=60°,∴∠EAC=∠ECA =30°,∴∠BAC =∠BAE +∠EAC = 90°,由勾股定理得 即平行线 AB 与DC 间的距离是
8.(1)【证明】∵ E 为 AB 的中点,∴ AB =2AE.
又∵AB=2CD,∴CD=AE.又∵AB∥CD,即AE∥CD,∴四边形AECD 是平行四边形.
∵ AC平分∠DAB,∴∠DAC=∠EAC.∵ AB∥CD,∴ ∠DCA=∠EAC.∴∠DCA =∠DAC.
∴ AD= CD. ∴ 四边形AECD 是菱形.
(2)【解】∵ 四边形 AECD 是菱形,CD =2,∠D=120°,
∴CE=AE =CD=2,AB =2CD=4,∠AEC=∠D = 120°.
∴ AE = BE = CE =2,∠CEB = 60°,∠CAE= ∠ACE =30°.
∴ △CEB 是等边三角形.∴BC=CE =2,∠BCE=60°.∴∠ACB =∠BCE +∠ACE=90°.
在 Rt△ABC 中,
9.(1)【证明】∵AC 平分∠BAD,∴∠DAC=∠BAC.
在△ADC 和△ABC中, ∴△ADC≌△ABC,∴AD=AB,CD=CB.
∵AB∥CD,∴∠DCA=∠BAC,∴ ∠DAC=∠DCA,∴AD=CD,
∴AD=AB=CD=CB,∴ 四边形ABCD 是菱形.
(2)【解】∵ 四边形ABCD 是菱形,BD=2,∴AC⊥
延长EO到点F,使OF=EO,连接AF.
∵AO=CO,∠AOF=∠COE,∴ △AOF≌△COE,∴ AF =CE,∠F=∠CEO,∴AF∥CE,
∴∠FAE+∠CEA=180°.
∵ CE⊥AB,∴ ∠AEC = 90°,∴ ∠EAF =∠AEC=90°.
又∵ AE = EA,∴ △AEC ≌△EAF,
10.【证明】(1)如图,过点 B 作BM∥AC 交 DC 的延长线于点M,则∠ACD =∠M.
∵ AB∥CD,∴ 四边形ABMC 为平行四边形.
又
又∵
(2)如图,连接 EH,HF,FG,GE.
∵ E,F,G,H 分别是AB,CD,AC,BD 的中点,
∥且 ∥且 ∥FG,HE = FG.
∴ 四边形 HFGE 为平行四边形.
由(1)知, 为菱形.
∴线段 EF 与线段 GH 互相垂直平分.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
