第六章 特殊平行四边形 1 菱形的性质与判定 第1课时 菱形的性质(含答案)
文档属性
| 名称 | 第六章 特殊平行四边形 1 菱形的性质与判定 第1课时 菱形的性质(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-29 09:16:28 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第六章 特殊平行四边形
1 菱形的性质与判定
第1课时 菱形的性质
基 础 练
练点1 菱形的定义及其对称性
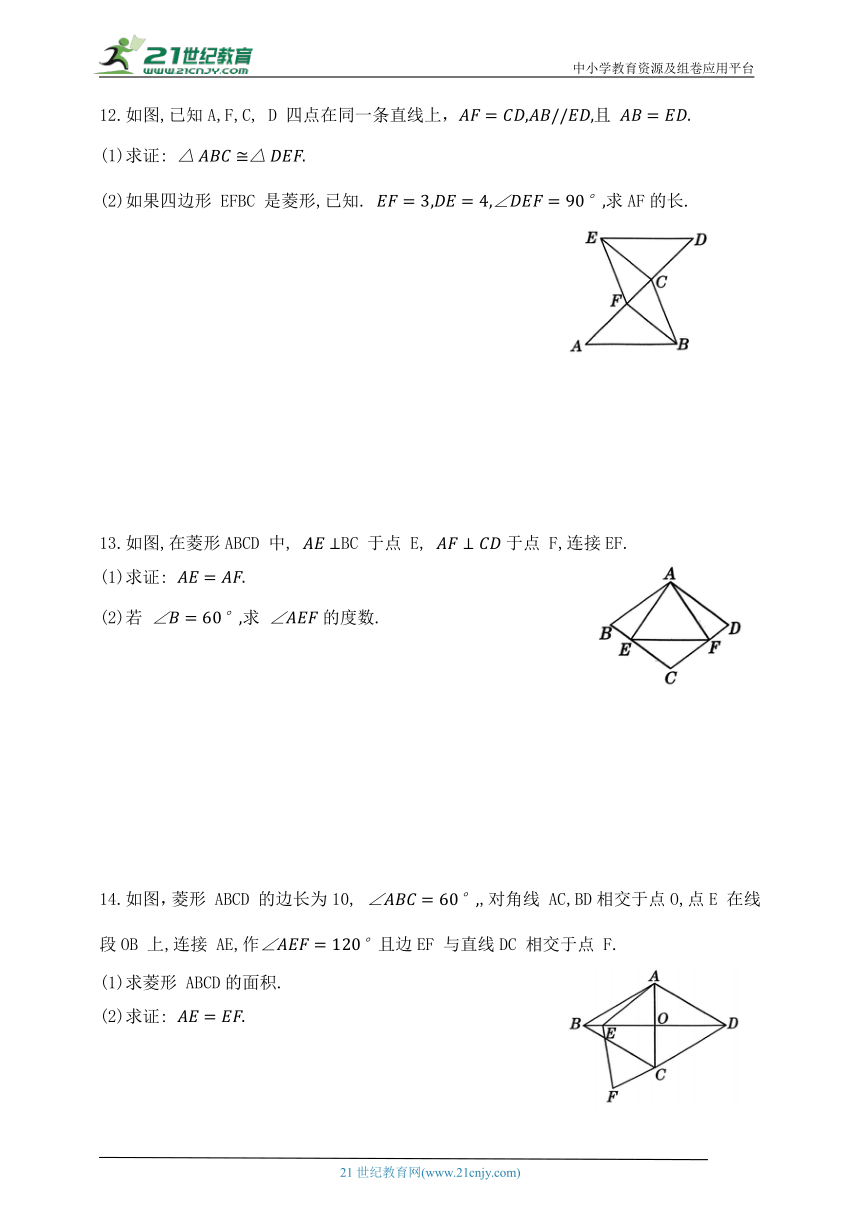
1.如图,要使 ABCD是菱形,则需添加的一个条件是( )
A. AC=AD B. BA=BC C.∠ABC=90° D. AC =BD
(第1题) (第2题)
2.如图,菱形ABCD的对角线交点与坐标原点O 重合,点A(-2,5),则点C的坐标是( )
A.(5,-2) B.(2,-5) C.(2,5) D.(-2,-5)
练点2 菱形的边的性质
3.如图,在菱形ABCD 中,对角线AC,BD 相交于点O,点 E 为 CD 的中点. 若OE=3,则菱形ABCD的周长为( )
A.6 B.12 C.24 D.48
(第3 题) (第4题)
4.如图,若菱形 ABCD的顶点A,B的坐标分别为(3,0),(-2,0),点 D 在y 轴上,则点D 的坐标是__________.
5.如图,在菱形 ABCD 中,E,F 是对角线 AC 上两点,连接 DE,DF, 求证:
练点3 菱形的对角线的性质
6.若菱形的两条对角线长分别为6和8,则该菱形的面积为__________.
7.点 E 是菱形ABCD的对称中心, ∠B=56°,连接AE,则∠BAE的度数为__________.
提 升 练
8.如图,菱形ABCD的边长为13,对角线AC=24,点E,F分别是边 CD,BC 的中点,连接EF 并延长与AB的延长线相交于点G,则EG的长为( )
A.13 B.10 C.12 D.5
(第8题) (第9题)
9.如图,点P 是边长为1的菱形ABCD的对角线AC 上的一个动点,点M,N分别是 AB,BC 边的中点,则MP +PN的最小值是( )
A.0.5 B.1 C. D.2
10.如图,四边形ABCD 为菱形, 延长BC到 E,在 内作射线 CM,使得过点 D作 垂足为 F.若 则 BD 的长为__________(结果保留根号).
11.如图,线段AB,CD端点的坐标分别为 2),B(3,-1),C(3,2),D(-1,5),将CD 平移至第一象限内,得到均在格点上).若四边形 是菱形,则所有满足条件的点. 的坐标为___________.
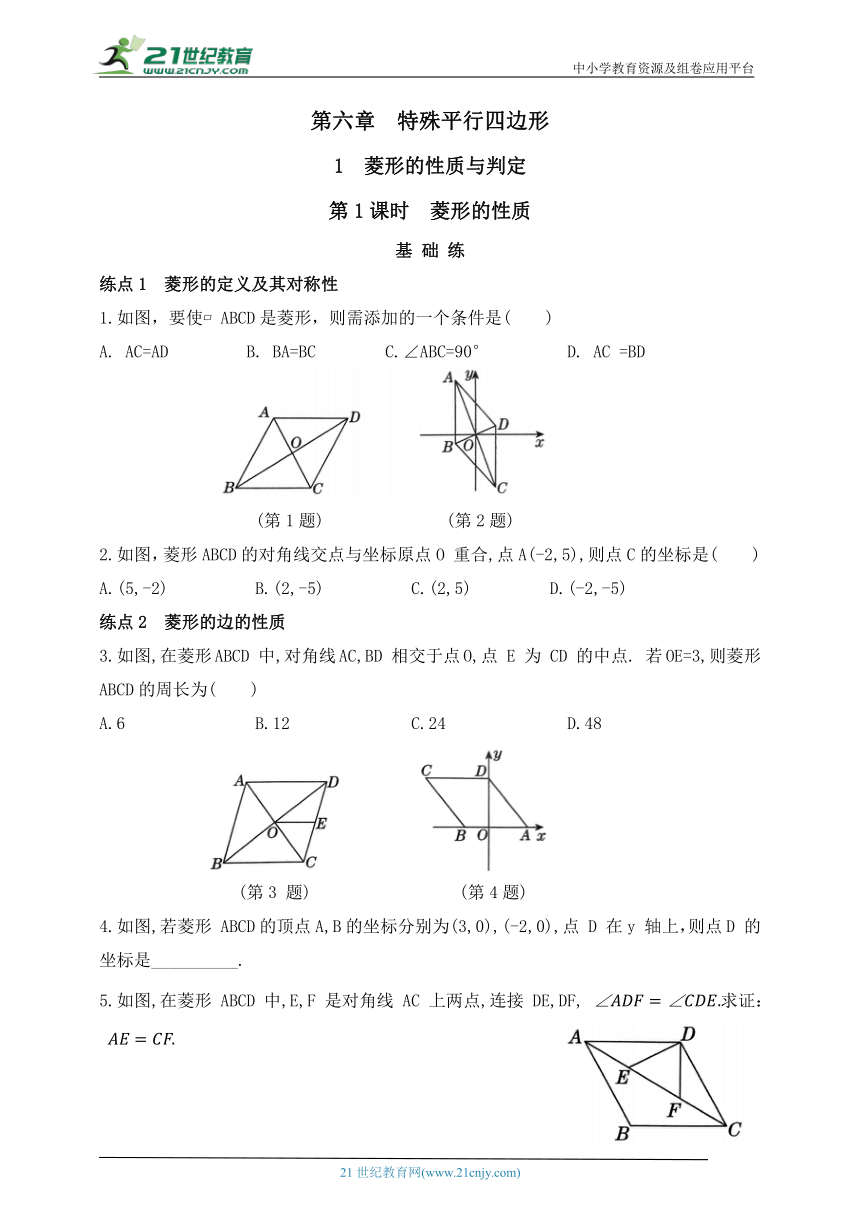
12.如图,已知A,F,C, D 四点在同一条直线上,且
(1)求证:
(2)如果四边形 EFBC 是菱形,已知. 求AF的长.
13.如图,在菱形ABCD 中, BC 于点 E, 于点 F,连接EF.
(1)求证:
(2)若 求 的度数.
14.如图,菱形 ABCD 的边长为10, ,对角线 AC,BD相交于点O,点E 在线段OB 上,连接 AE,作且边EF 与直线DC 相交于点 F.
(1)求菱形 ABCD的面积.
(2)求证:
参考答案
1. B 2. B
3. C 【点拨】∵ 四边形 ABCD 为菱形,
,点 E 为线段 CD 的中点,∴ OE 是 的中位线,
∴菱形ABCD的周长=4AD=4×6=24.
4.(0,4) 【点拨】∵ 菱形 ABCD的顶点 A,B 的坐标分别为(3,0),(-2,0),∴ AO =3,OB =2,∴ AB =AO+OB=5,∴AD=AB=5,∴DO=
∵点 D在y轴上,∴ 点D(0,4).
5.【证明】∵ 四边形ABCD是菱形,∴DA=DC,∴∠DAC=∠DCA.∵∠ADF=∠CDE,
∴∠ADF-∠EDF=∠CDE-∠EDF,∴∠ADE=∠CDF.
在△DAE和△DCF中 ∴△DAE≌△DCF(ASA),∴ AE=CF.
6.24
7.62° 【点拨】如图,连接 BE,
∵点E是菱形 ABCD 的对称中心,∴ 点 E 是菱形 ABCD 的两对角线的交点,
8. B 【点拨】连接BD,交AC 于点O,∵菱形ABCD的边长为13,AC=24,
∴ AB∥CD,CD=13,AC⊥BD,
在Rt△COD中,OD=
∵点 E,F 分别是边CD,BC 的中点,∴ EF 是△CBD 的中位线,∴EF∥BD.
∴四边形BDEG 是平行四边形,∴EG=BD=10.
点方法 已知菱形, 要求线段的长, 通常应用菱形的对角线互相垂直平分并结合勾股定理求解.如果菱形的对角线在图形中没有出现, 需先作出对角线.
9. B 【点拨】如图,取AD的中点 连接 则有 MP =M'P.
所以 MP +PN的最小值为线段 M'N的长,易得 M'N=CD=1.
10.2 【点拨】连接AC,交 BD 于点 H,由菱形的性质得40°,∠DCE = 80°,∠DHC = 90°.
又∵∠ECM =30°,∴∠DCF =50°.
∵DF⊥CM,∴∠CFD =90°, ∴∠CDF =40°,∴∠HDC =∠FDC.
在△CDH 和△CDF 中, ∴ △CDH≌△CDF(AAS),
∴DH=DF = ,∴DB=2DH =2
11.(3,5)或(2,6) 【点拨】如图,
∵A(-1,2),B(3,-1),C(3,2),D(-1,5),∴AB∥CD,AB=CD=5.
以A为圆心,AB长为半径画弧,此弧经过第一象限的格点 6),D"(4,2).
将线段 CD向右平移4个单位得线段C'D',此时四边形. 是菱形,点 C'的坐标是(7,2),在第一象限;将线段CD向右平移3个单位,向上平移1 个单位得线段 C"D",此时四边形 是菱形,C"的坐标是(6,3),在第一象限;将线段 CD向右平移5个单位,向下平移3个单位得线段 C''D'',此时四边形ABC''D''是菱形,C''的坐标是(8,-1),在第四象限. 所以满足条件的点 D'的坐标是(3,5)或(2,6).
12.(1)【证明】∵ AB∥DE,∴∠A=∠D.
∵AF=CD, ∴AF + FC = CD + FC,即AC = DF.
在△ABC 和△DEF中
(2)【解】连接 EB 交 AD 于点 O.
在 Rt△EFD 中,
四边形EFBC是菱形,
13.(1)【证明】∵ 四边形 ABCD 是菱形, ∠B=∠D.
又∵AE⊥BC 于点E,AF⊥CD于点F,∴ ∠AEB =∠AFD =90°.
在△ABE 与△ADF 中,
(2)【解】∵ 四边形 ABCD 是菱形,∴AD∥BC,∴∠B+∠BAD =180°.
∵∠B =60°,∴ ∠BAD=120°.
又∵∠AEB=90°,∠B=60°,∴∠BAE=30°.
由(1)知△ABE≌△ADF,∴∠BAE=∠DAF=30°.
.
又∵ AE = AF,∴△AEF是等边三角形.∴ ∠AEF=60°.
14.(1)【解】过点A 作AG⊥BC交BC 于点 G.
∵四边形ABCD 是菱形,边长为 10,∴ AB = BC = 10.
∵∠ABC=60°,∴ △ABC 是等边三角形,∴BG=
∴ 菱形 ABCD 的面积
(2)【证明】连 接 EC.
∵ 四边形 ABCD 是菱形,∠ABC=60°,∴ BD 垂直平分 AC,
又∵∠ECA+∠ECF=1,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 特殊平行四边形
1 菱形的性质与判定
第1课时 菱形的性质
基 础 练
练点1 菱形的定义及其对称性
1.如图,要使 ABCD是菱形,则需添加的一个条件是( )
A. AC=AD B. BA=BC C.∠ABC=90° D. AC =BD
(第1题) (第2题)
2.如图,菱形ABCD的对角线交点与坐标原点O 重合,点A(-2,5),则点C的坐标是( )
A.(5,-2) B.(2,-5) C.(2,5) D.(-2,-5)
练点2 菱形的边的性质
3.如图,在菱形ABCD 中,对角线AC,BD 相交于点O,点 E 为 CD 的中点. 若OE=3,则菱形ABCD的周长为( )
A.6 B.12 C.24 D.48
(第3 题) (第4题)
4.如图,若菱形 ABCD的顶点A,B的坐标分别为(3,0),(-2,0),点 D 在y 轴上,则点D 的坐标是__________.
5.如图,在菱形 ABCD 中,E,F 是对角线 AC 上两点,连接 DE,DF, 求证:
练点3 菱形的对角线的性质
6.若菱形的两条对角线长分别为6和8,则该菱形的面积为__________.
7.点 E 是菱形ABCD的对称中心, ∠B=56°,连接AE,则∠BAE的度数为__________.
提 升 练
8.如图,菱形ABCD的边长为13,对角线AC=24,点E,F分别是边 CD,BC 的中点,连接EF 并延长与AB的延长线相交于点G,则EG的长为( )
A.13 B.10 C.12 D.5
(第8题) (第9题)
9.如图,点P 是边长为1的菱形ABCD的对角线AC 上的一个动点,点M,N分别是 AB,BC 边的中点,则MP +PN的最小值是( )
A.0.5 B.1 C. D.2
10.如图,四边形ABCD 为菱形, 延长BC到 E,在 内作射线 CM,使得过点 D作 垂足为 F.若 则 BD 的长为__________(结果保留根号).
11.如图,线段AB,CD端点的坐标分别为 2),B(3,-1),C(3,2),D(-1,5),将CD 平移至第一象限内,得到均在格点上).若四边形 是菱形,则所有满足条件的点. 的坐标为___________.
12.如图,已知A,F,C, D 四点在同一条直线上,且
(1)求证:
(2)如果四边形 EFBC 是菱形,已知. 求AF的长.
13.如图,在菱形ABCD 中, BC 于点 E, 于点 F,连接EF.
(1)求证:
(2)若 求 的度数.
14.如图,菱形 ABCD 的边长为10, ,对角线 AC,BD相交于点O,点E 在线段OB 上,连接 AE,作且边EF 与直线DC 相交于点 F.
(1)求菱形 ABCD的面积.
(2)求证:
参考答案
1. B 2. B
3. C 【点拨】∵ 四边形 ABCD 为菱形,
,点 E 为线段 CD 的中点,∴ OE 是 的中位线,
∴菱形ABCD的周长=4AD=4×6=24.
4.(0,4) 【点拨】∵ 菱形 ABCD的顶点 A,B 的坐标分别为(3,0),(-2,0),∴ AO =3,OB =2,∴ AB =AO+OB=5,∴AD=AB=5,∴DO=
∵点 D在y轴上,∴ 点D(0,4).
5.【证明】∵ 四边形ABCD是菱形,∴DA=DC,∴∠DAC=∠DCA.∵∠ADF=∠CDE,
∴∠ADF-∠EDF=∠CDE-∠EDF,∴∠ADE=∠CDF.
在△DAE和△DCF中 ∴△DAE≌△DCF(ASA),∴ AE=CF.
6.24
7.62° 【点拨】如图,连接 BE,
∵点E是菱形 ABCD 的对称中心,∴ 点 E 是菱形 ABCD 的两对角线的交点,
8. B 【点拨】连接BD,交AC 于点O,∵菱形ABCD的边长为13,AC=24,
∴ AB∥CD,CD=13,AC⊥BD,
在Rt△COD中,OD=
∵点 E,F 分别是边CD,BC 的中点,∴ EF 是△CBD 的中位线,∴EF∥BD.
∴四边形BDEG 是平行四边形,∴EG=BD=10.
点方法 已知菱形, 要求线段的长, 通常应用菱形的对角线互相垂直平分并结合勾股定理求解.如果菱形的对角线在图形中没有出现, 需先作出对角线.
9. B 【点拨】如图,取AD的中点 连接 则有 MP =M'P.
所以 MP +PN的最小值为线段 M'N的长,易得 M'N=CD=1.
10.2 【点拨】连接AC,交 BD 于点 H,由菱形的性质得40°,∠DCE = 80°,∠DHC = 90°.
又∵∠ECM =30°,∴∠DCF =50°.
∵DF⊥CM,∴∠CFD =90°, ∴∠CDF =40°,∴∠HDC =∠FDC.
在△CDH 和△CDF 中, ∴ △CDH≌△CDF(AAS),
∴DH=DF = ,∴DB=2DH =2
11.(3,5)或(2,6) 【点拨】如图,
∵A(-1,2),B(3,-1),C(3,2),D(-1,5),∴AB∥CD,AB=CD=5.
以A为圆心,AB长为半径画弧,此弧经过第一象限的格点 6),D"(4,2).
将线段 CD向右平移4个单位得线段C'D',此时四边形. 是菱形,点 C'的坐标是(7,2),在第一象限;将线段CD向右平移3个单位,向上平移1 个单位得线段 C"D",此时四边形 是菱形,C"的坐标是(6,3),在第一象限;将线段 CD向右平移5个单位,向下平移3个单位得线段 C''D'',此时四边形ABC''D''是菱形,C''的坐标是(8,-1),在第四象限. 所以满足条件的点 D'的坐标是(3,5)或(2,6).
12.(1)【证明】∵ AB∥DE,∴∠A=∠D.
∵AF=CD, ∴AF + FC = CD + FC,即AC = DF.
在△ABC 和△DEF中
(2)【解】连接 EB 交 AD 于点 O.
在 Rt△EFD 中,
四边形EFBC是菱形,
13.(1)【证明】∵ 四边形 ABCD 是菱形, ∠B=∠D.
又∵AE⊥BC 于点E,AF⊥CD于点F,∴ ∠AEB =∠AFD =90°.
在△ABE 与△ADF 中,
(2)【解】∵ 四边形 ABCD 是菱形,∴AD∥BC,∴∠B+∠BAD =180°.
∵∠B =60°,∴ ∠BAD=120°.
又∵∠AEB=90°,∠B=60°,∴∠BAE=30°.
由(1)知△ABE≌△ADF,∴∠BAE=∠DAF=30°.
.
又∵ AE = AF,∴△AEF是等边三角形.∴ ∠AEF=60°.
14.(1)【解】过点A 作AG⊥BC交BC 于点 G.
∵四边形ABCD 是菱形,边长为 10,∴ AB = BC = 10.
∵∠ABC=60°,∴ △ABC 是等边三角形,∴BG=
∴ 菱形 ABCD 的面积
(2)【证明】连 接 EC.
∵ 四边形 ABCD 是菱形,∠ABC=60°,∴ BD 垂直平分 AC,
又∵∠ECA+∠ECF=1,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
